Алексеев В.В. Физическое и математическое моделирование экосистем

Подождите немного. Документ загружается.

ществование только простых стационарных режимов

—

однокомпо-

нентных

двухкомпонентных сообществ.

В.

Алексеевым

[9]

была предложена модель конкуренции

между

микроводорослями

замкнутой экосистеме

описанием

механизма лимитирования

точном соответствии

принципом

Либиха (второй вариант описания смены лимитирования,

см.

п.

2.5).

Модель была построена

предположении,

что

элементный

химический состав организмов фиксирован

каждый

вид по-

требляет биогены

в про-

порциях, соответствующих

соотношению элементов

клетках водоросли. Напри-

мер,

i-я

популяция водорос-

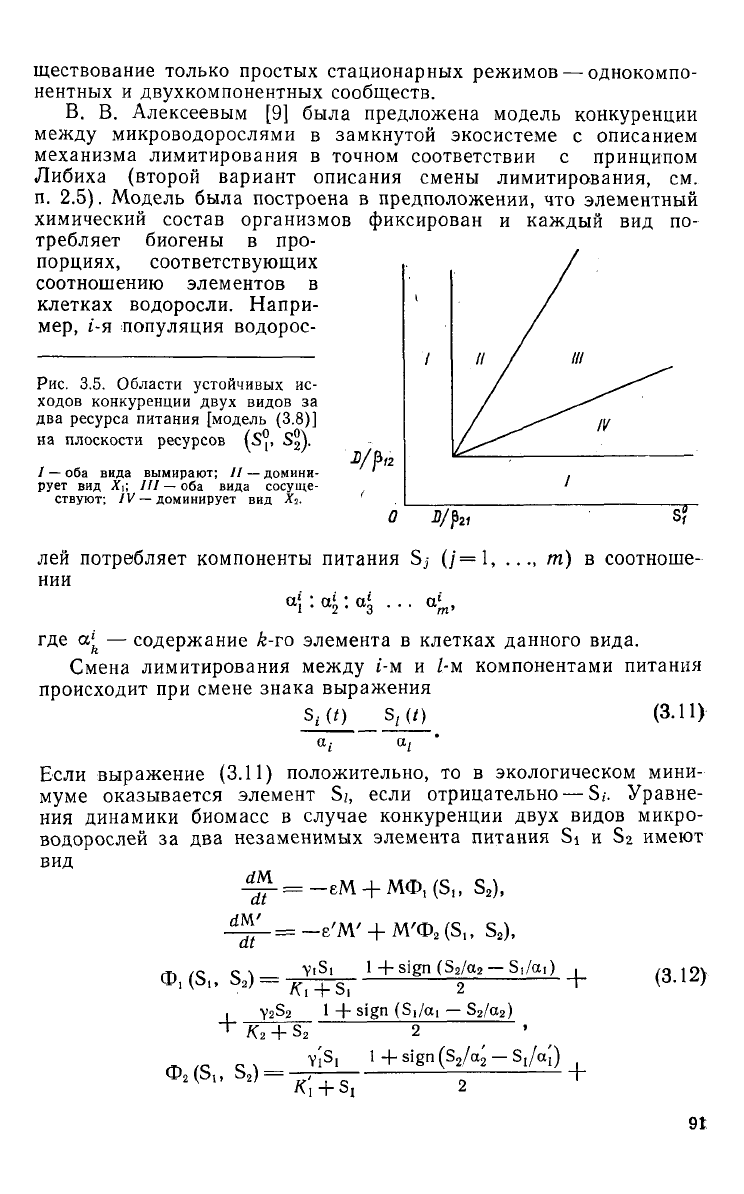
Рис.

3.5.

Области

устойчивых

ис-

ходов

конкуренции

двух

видов

за

два

ресурса

питания

[модель

(3.8)]

на плоскости

ресурсов

(S°, Sj).

/ — оба вида вымирают;

— домини-

рует

вид Хи III

— оба вида сосуще-

ствуют;

— доминирует

вид Xi.

I II

л/}„

лей потребляет компоненты питания

(/=1,

..., /п) в

соотноше-

нии

где

—

содержание

&-го

элемента

клетках данного вида.

Смена лимитирования

между

г-м и

1-м компонентами питания

происходит при смене знака выражения

МО

«)

(3.11)

а,-

а,

Если выражение

(3.11)

положительно,

то в

экологическом мини-

муме

оказывается элемент

S;,

если отрицательно

—

S/. Уравне-

ния

динамики биомасс

случае

конкуренции

двух

видов микро-

водорослей

за два

незаменимых элемента питания

Si и S2

имеют

вид

S,, S

YiSi

-fsign

—

Si/cti)

tfi+S,

1 +

sign

)

(3.12)

к*

+ sign

/ct2

+ S

где М—биомасса вида (на 1 объем воды); е — коэффициенты

естественной смертности; уи

у-г

— максимальные скорости приро-

ста биомассы вида М при лимитировании биогенами Si и S2;

Ki, Кг — константы полунасыщения для вида М при лимитирова-

нии

биогенами Si, S2; обозначения со штрихом соответствуют ве-

личинам,

характеризующим биомассу вида М'.

Первоначально

рассмотрим модель конкуренции для системы

с замкнутым круговоротом элементов питания. Условия сохране-

ния

общего запаса каждого из элементов имеют вид

a,M + ajM'+ S, = Л„

aM'

+ S 4

(ЗЛЗ)

где А\, Аг — общие запасы первого и второго элементов питания

системе.

Прежде чем приступить к выкладкам, сделаем одно замечание

относительно специфики модели

(3.12)

— (3.13). В модели предпо-

лагается, что смена лимитирующего биогена для всей популяции

происходит мгновенно, это и отражает функция

sign

(x). В любой

момент времени выполняется принцип Либиха, и скорость роста

определяется одним лимитирующим биогеном. Однако очевидно,

что в реальных системах смена лимитирования совершается за не-

который

промежуток времени, в течение которого принцип Либиха

не

выполняется ни для отдельных организмов, ни для популяции

целом. Поскольку адаптационные процессы, сопровождающие

смену лимитирования, в модели не учитываются, для уравнений

(3.12)—(3.13)

характерно скачкообразное изменение скоростей

роста биомасс при смене лимитирующего фактора.

Наше

исследование стационарных исходов конкуренции в си-

стеме

(3.12)

—

(3.13)

будет

заключаться в выделении набора обла-

стей, не содержащих переключений по лимитированию, и опреде-

лении

всех устойчивых стационарных точек, возможных в каждой

такой

области. Объединение результатов

даст

полную картину

конкуренции

в фитоценозе. В общем

случае

размеры областей

устойчивости зависят от параметров А{ и

А-±,

характеризующих

общие запасы биогенов в системе, а также от начальных значений

биомасс М(0), М'(0). Поэтому теоретический расчет

будет

сопро-

вождаться иллюстрацией результатов на плоскости биогенов (А;,

)

и на фазовой плоскости (М, М') [24].

Упростим выражения, стоящие под знаком

sign

в (3.12), вы-

разив Si и S

через М и М' с помощью уравнений (3.13). По-

лучим

sign

—

S,/a,)

sign

(a,S

— a

S,) =

sign

(tf, — 6M'),

sign(S

— S,/aJ)==sign(#

-f 6M),. ^

где через Я

Яг, б обозначены комбинации параметров

Н,

= а

— а

Д,

= а[А

— а

{

(3.15)

6 = а

{

а'

— а

а|.

Для определенности

будем

считать, что б—положительная вели-

чина,

т. е.

a,/a

>a;/a;.

(3.16)

Величины Hi и Я

зависят лишь от параметров A

, что позво-

ляет разбить положительный квадрат плоскости биогенов (А\, Аг)

на

три сектора с фиксированными знаками Hi, Я

, а именно:

сектор I {А

> Л^/а,'), где Я

> О, Я

> 0;

сектор II (a

/ai< Л2/Л1 < c^/a'), где Я

> 0, Я

< 0;

сектор III (Л

< Л^г/а^, где Я

< 0, Я

< 0.

Дальнейшее рассмотрение системы

(3.12)

—

(3.13)

будет

прово-

диться по каждому сектору плоскости (Л

) в отдельности.

В секторе I функция

sign

(Я2+6М) положительна независимо

от величины М, поэтому

всюду

в секторе популяция М' лимити-

руется концентрацией биогена Si. Динамика популяции М' опре-

деляется уравнением

eM+Mv

'<Ti7'

(ЗЛ7)eM+Mv

'<Ti7'

Выражение

sign

(Я

— 6М'), определяющее динамику роста по-

поляции

М, может иметь разные

знаки.

Зависимость скорости

роста вида М от начальной плотности популяции М' (0) выража-

ется следующим образом: при М' < Я

/б

if- = -eM + M

Yll

^-, (3.18)

т. е. лимитирующим фактором является биоген Sr, при М' > Я^б

+ M

^_,

(3.19)

лимитирующим оказывается биоген S

Прямая

W=Hi/8 разбивает, таким образом, фазовую плос-

кость (М, М') на две области: в полосе, прилегающей к оси М',

динамика

фитоценоза определяется уравнениями

(3.17)

и (3.18),

на

остальной части плоскости — уравнениями

(3.17)

и (3.19).

Анализ устойчивости стационарных состояний (для малых откло-

нений)

показал, что при М' < Я1/6 в фитоценозе нет устойчивых

особых точек. Рассмотрение стационарных точек при М/ < Я]/б

дает

следующие результаты.

Нулевое состояние фитоценоза устойчиво при условии

min(e,,

e;),

гК

{

t'K\

(3.20>

;

= ,

И,

—т

т ,

— е Yi —

где

6i, 0'j —

минимальные концентрации биогена

Si в

среде, необ-

ходимые

для

существования соответственно видов

М и М'.

Если общий запас биогена

превышает критическое значе-

ние,

определяемое (3.20),

то

устойчивым доминантой

системе

становится

вид,

осуществляющий минимум

из 6i и 6^.

В итоге сектор

плоскости

{А

)

разделяется прямой

min

(0!, 0j) на

«мертвую»

зону

зону доминирования популя-

ции,

наиболее неприхотливой

по

отношению

биогену

Si.

Этот

результат

является вполне естественным,

так как в

секторе

примыкающем

к оси А

биоген

становится дефицитным

для

обеих популяций.

Совершенно аналогичные результаты получаются

при

рассмот-

рении

сектора

III, где

лимитирующим является биоген

Наибольший интерес представляет исследование конкуренции

в среднем секторе

плоскости биогенов

при

аг/ai

А2/А1

< o^/a'j. Близкие

по

величине запасы обоих минеральных компо-

нентов питания предполагают сложные конкурентные взаимоотно-

шения

между

популяциями.

В секторе

знаки обеих сигнатур

(3.14)

могут

меняться

в за-

висимости

от

биомасс популяций

М и М'.

Выпишем уравнения динамики фитоценоза

для

каждой

из че-

тырех возможных ситуаций.

При

М<|Я

|/б;

М' <

Hi/6 имеем

приМ<|Я

|/б;

w (-E

(3-22)

приМ>|Я

|/б;М'<Я

/б

rfM

-мС-е

4- v

(3.23)

при М>|Я

|/6; М'

>HJ6

~dT

= 1

, Si

•

= М I—

+ V, ^гт—

(3.24)

Вариант динамики (3.21) описывает область лимитирования

разными

биогенами: популяции

М —

биогеном

Si,

популяции

М' —

биогеном

Бг. Эта

конкурентная ситуация может иметь четыре

ис-

хода.

Перечислим

их.

Вымирание

обеих

популяций (М = О, М' = 0)

Это состояние устойчиво, когда

< 0,; А, < Э;,

(3.25)

где

_1^

(3.26)

•Y2

—

минимальная концентрация биогена

необходимая

для вы-

живания

вида

М'; 0i

определяется

из

(3.20)).

В дальнейшем местоположение точки

%'Л

на

плоскости

за-

пасов биогенов

(Аи А

)

будет

для нас

существенно, поэтому

определим сразу условия

ее

нахождения

каждом

из

секторов

I—III. Точка (01,

0^)

принадлежит:

сектору

если

0,/0

а;/а

(3.27)

сектору II, если

;/а

< е,/е; < уа,,

(3.28)

сектору

III,

если

0,/0

а,/а

(3.29)

Доминирование вида М' (М = 0; М' ф 0)

Плотность

популяции

концентрации биогенов

этом случае

устанавливаются

на

уровне

М'

(Л

-0

)/а

= 0; S

= 0

(3.30)

-(A

-Q'

)a'

/a'

Этот исход является устойчивым

при

следующих ограничениях

на

параметры:

А>е

(3.31)

Л>^-Л

е;--^-е;,

(3.32)

а,

(

а,

\ а

Выражения (3.32),

(3.33)

определяют

на

плоскости

(Ai, Аг) пря-

мые, параллельные верхнему

лучу

сектора

II.

Прямая

(3.32)

про-

ходит

через точку

(8i,

прямая (3.33)—через точку пересече-

ния

ординаты

=в'

нижним лучом сектора

II.

Нетрудно видеть,

что

область доминирования вида

М'

оказы-

вается пустой, если точка

(0i,

0£)

принадлежит

сектору,

имеет

вид полосы, примыкающей

верхнему

лучу

среднего сектора

остальных случаях.

Доминирование вида М (М'

= 0;

ф 0)

Стационарная

плотность популяции

М и

концентрации биогенов

определяются формулами

(Д-е

)/а

М'

S,=e,,

(3.34)

= А

—

(А

—

01)

г/

•

Условия положительности

устойчивости данного стационара

следующие:

> е„

(3.35)

А<

—

(А-е,)

^-0,- (3.37)

а,

о,

Прямые

(3.36)

(3.37) параллельны нижнему

лучу

сектора

II,

проходят соответственно через точку

(8i, 0

') и

точку пересече-

ния

абсциссы

А\ = 8i с

верхним лучом. Область устойчивости

пу-

ста, если точка

(0i, 0^)

лежит

в III

секторе плоскости биогенов,

ограничена полосой, примыкающей

нижней границе среднего

сектора

двух

других случаях.

Сосуществование

видов МиМ'

В установившемся режиме состояние фитоценоза описывается

формулами

M=[a'

-Q

)-a[(A

-Q'

)]/6,

[а, (А,

)

- а

(А -

е,)]/о,

(3.38)

S, =0,;

02-

Стационарные

плотности биомасс положительно определены ме-

жду прямыми

(3.32)

(3.36)

с дополнительным условием (3.28).

Состояние

устойчиво с

учетом

(3.16)

всюду

в области существо-

вания.

Таким образом, конкурирующие виды М и М'

могут

сосу-

ществовать, если параметры Ai и Л

заданы внутри области,

имеющей вид сектора с вершиной в точке (0i, 6^) и сторонами,

параллельными

лучам

сектора II. Подчеркнем, кроме того, что

два вида

могут

сосуществовать только в том случае, когда точка

8^) принадлежит среднему сектору плоскости биогенов.

Вариант динамики фитоценоза (3.24), так же, как и (3.21),

описывающий лимитирование популяций разными биогенами, не

имеет устойчивых состояний равновесия.

Вариант динамики (3.22), когда оба вида ограничены S2,

имеет один стационар (доминирование популяции М'), совпадаю-

щий

по значению с (3.30). Область устойчивости, однако, отли-

чается от

(3.31)

—

(3.33)

и ограничена совместным выполнением

неравенств

е; < е

. (3.40)

На

плоскости (А

Ai) доминирование вида М' с плотностью

популяции,

превышающей величину #i/б (условие, при котором

справедливы уравнения (3.22)), возможно в секторе с вершиной

точке ((ai/Gteje^; Q'A, нижним лучом совпадающим и верхним

лучом параллельным соответствующим

лучам

сектора II. Сле-

дует

отметить, что состояние устойчиво, если вид М' более непри-

хотлив по отношению к биогену Бг, чем вид М, т. е. когда 0^ < 6г.

Это требование естественно, так как оба вида конкурируют за S2.

Уравнения (3.23), характеризующие конкуренцию популяций

за компонент питания Si, имеют одну равновесную точку — доми-

нирование

вида М. Плотность биомассы и концентрации биогенов

определяются формулами (3.34). Положительность и устойчивость

равновесия достигается при выполнении условия

(3.35)

и нера-

венств

Л> —

(А-е,)

+ ^-е

(3.41)

8, < 8J.

(3.42)

Область доминирования вида М с плотностью биомассы выше

значения

|Яг|/б

имеет вид сектора с вершиной в точке (0i;

(а

/а'Л0\ у которого верхний луч совпадает, а нижний паралле-

лен соответствующим

лучам

сектора П. В данном

случае

доми-

нирующей оказывается популяция с наименьшей потребностью

биогенном элементе Si.

Заказ

№ 57 97

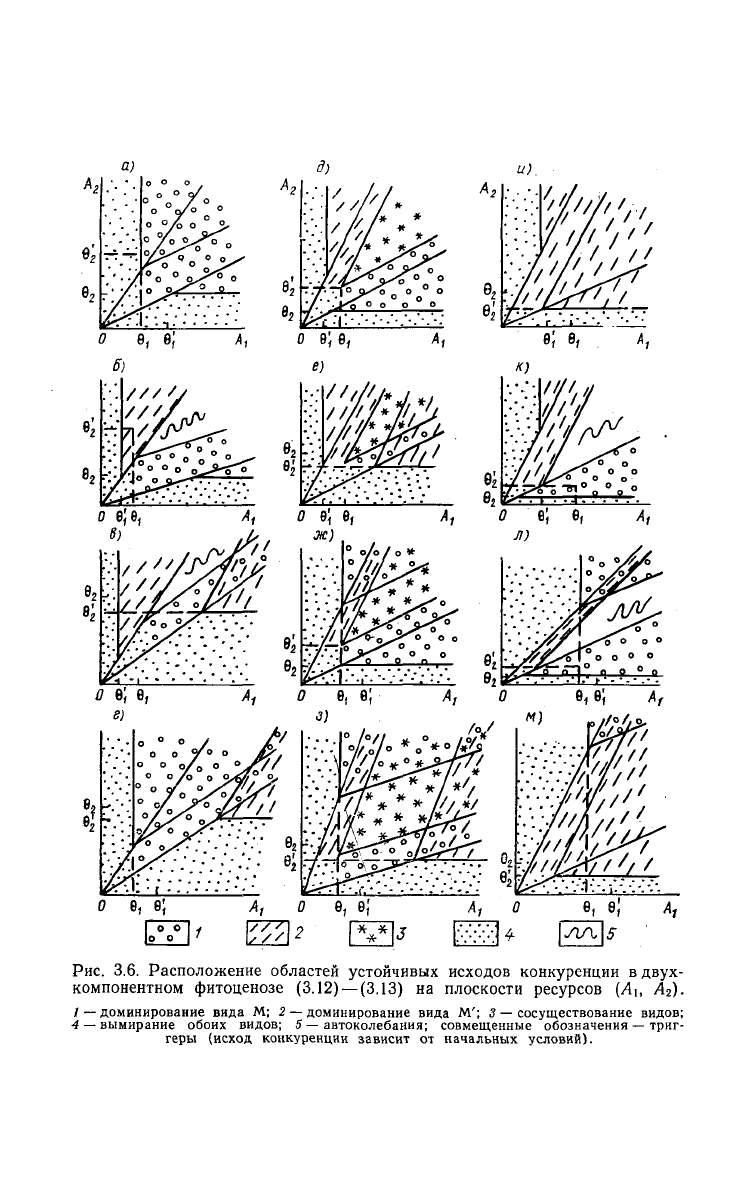
Рис.

3.6. Расположение областей устойчивых исходов конкуренции

вдвух-

компонентном фитоценозе

(3.12) —(3.13)

на плоскости ресурсов (A

—

доминирование вида

М; 2 —

доминирование вида

М'; 3 —

сосуществование видов;

—

вымирание обоих видов; 5—автоколебания; совмещенные обозначения

—

триг-

геры (исход конкуренции зависит

от

начальных условий).

Результаты теоретических расчетов представлены на рис. 3.6

виде вариантов разбиения плоскости биогенов (Ai, A

) на об-

ласти устойчивых исходов конкуренции

между

водорослями. Всего

возможно 12 различных способов заполнения плоскости биогенов,

при

этом выделяются три группы вариантов в зависимости от

местоположения точки (0\, 0

'), т. е. от выполнения одного из не-

равенств

(3.27)

— (3.29). Рисунки 3.6 а—г относятся к

случаю

рас-

положения

точки (8i, Q'

) в I секторе; рис. 3.6 д—з — точка (8i,

6£) во II секторе; рис. 3.6 и—м — точка (0i, 0£) в III секторе.

Внутри каждой группы возможны 4 сочетания взаимного распо-

ложения

точек 0! и 8'

на оси Л

и точек 02, 6' на оси А

Напо-

мним,

что величины 0 определяют приспособленность популяций

дефициту того или иного биогенного элемента.

Нетрудно видеть, что кроме простых вариантов (см.

рис.

3.6а,д,и),

где области доминирования плотно прилегают

друг

другу,

существуют

варианты, когда различные исходы на-

кладываются, образуя двойные и

даже

тройные триггеры (области,

где исход конкуренции зависит от начальных значений биомасс).

В ряде случаев

между

границами областей имеются разрывы,

внутри которых

отсутствуют

какие-либо устойчивые равновесные

состояния

модели

(3.12)

— (3.13). Для замкнутой системы неустой-

2,4

•00

усл.

ед.

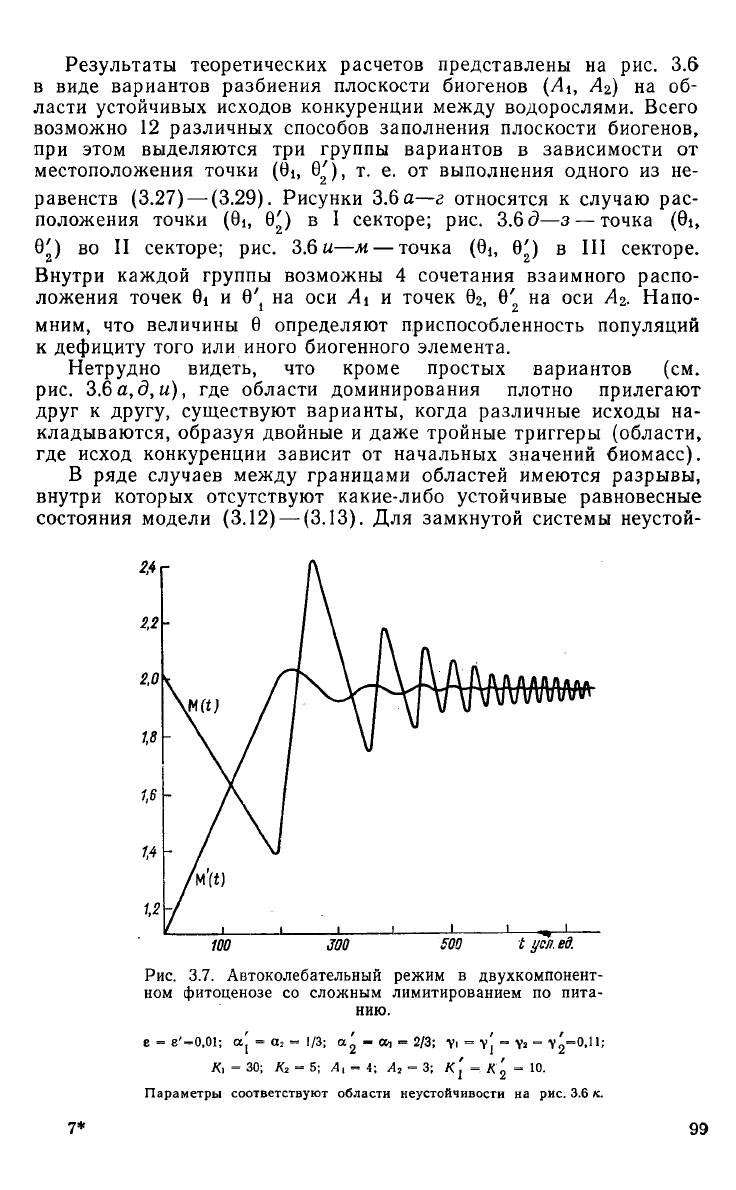
Рис.

3.7. Автоколебательный режим в двухкомпонент-

ном

фитоценозе со сложным лимитированием по пита-

нию.

е'=0,01;

[

= а?

Y, = Ys =

1/3; <х

- ои •= 2/3;

К, = 30; Кг = 5; Л, = 4; А, = 3;

Параметры

соответствуют

области неустойчивости на рис. 3.6 к.

чивость стационарных решений означает возникновение колебаний

биомасс. На рис. 3.7 показан режим автоколебаний биомасс водо-

рослей в фитоценозе, полученный интегрированием уравнений

(3.12),

(3.13)

на ЭВМ. Параметры, выбранные для расчета, соот-

ветствуют

на плоскости (А±, Аг) области неустойчивости на

рис.

3.6 к. Плотности биомасс колеблются с одинаковой частотой,

причем фазы сдвинуты на —. В процессе установления частота

менялась, что свидетельствует о приближении траекторий к пре-

дельному циклу.

Наличие триггерных ситуаций в фитоценозе становится понят-

ным,

если вспомнить, что системы уравнений

(3.21)

—

(3.24)

описы-

вают одну и ту же модель

(3.12)

—

(3.13)

при разных начальных

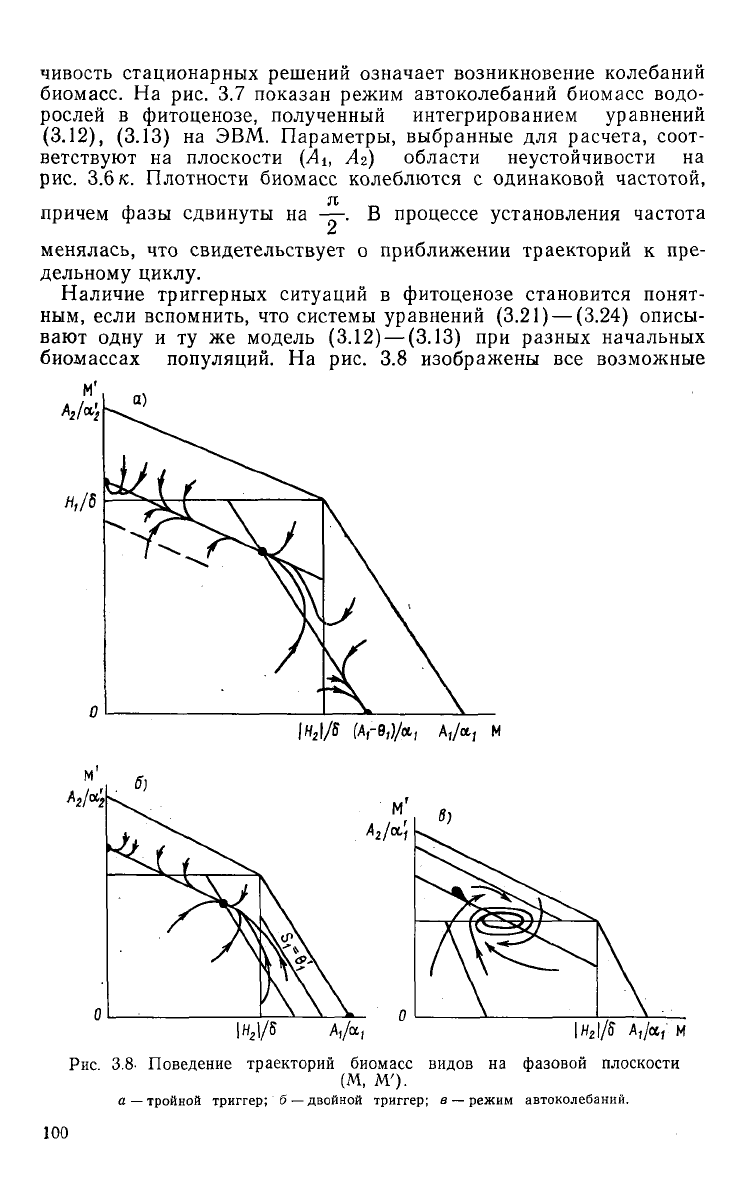
биомассах популяций. На рис. 3.8 изображены все возможные

Ш/6

(А

0,)/а,

А,/*, М

\н

\/8

А,/а, м

Рис.

3.8- Поведение траекторий биомасс видов на фазовой плоскости

(М,

М').

а — тройной триггер; б — двойной триггер; в — режим автоколебаний.

100