Алексеев Г.В. Классические методы математической физики. Часть 2
Подождите немного. Документ загружается.


′
Γ ∈ C
2,α
0 <
α < 1
u
+
∈ C
2,α
(Ω) u
−
∈ C
2,α
(Ω
e
)
Ω
′
= Ω
kuk
C
2,α
(
Ω)
≤ Ckρk
C
α
(Ω)
.
Γ u
x ∈ Γ
Γ R
n
u
Γ
˜
Ω
Ω ρ Ω
u(x) =
Z
˜
Ω
E
n
(x, y)˜ρ(y)dy.
˜ρ
˜ρ(x) = ρ(x) , x ∈ Ω ˜ρ(x) = 0, x ∈
˜
Ω\Ω.
(
˜
Ω, ˜ρ)
′
u|
˜
Ω
∈ C
2
(
˜
Ω)
u ∈ C
∞
(Ω
e
) u ∈ C
2
(R
n
)
C
l,α
(Ω)
˙
C
l,α
(Ω) = {ρ ∈ C
l,α
(Ω) : ˜ρ ∈ C
l,α
(R
n
)}, l ∈ N, 0 < α < 1,
˙
C
α
(Ω) =
˙
C
0,α
(Ω).
ρ ∈
˙
C
α
(Ω)
u C
2,α
(R
n
)
Ω
′
⊂ R
n
kuk
C
2,α
(
Ω
′
)
≤ Ckρk
C
α
(Ω)
.
C Ω
′
, n α
′
˜ρ
ρ(x) x → x
0
∈ Γ
ρ(x) x → x
0
∈ Γ

Γ
u
ρ
2m
2m
u
u
ρ
u Ω ρ ∈ C
1,α
(Ω) u
C
3,α
(Ω) ρ ∈
˙
C
1,α
(Ω) u ∈ C
3,α
(R
n
)
′
u
+
∈
C
2,α
(Ω) u
−
Ω
e
n ≥ 3 |x| → ∞
Γ ∈ C
2,α
u
+
∈ C
2,α
(Ω) u
−
∈ C
2,α
(Ω
e
)
ρ ∈
˙
C
α
(Ω) u ∈ C
2,α
(R
n
)
ρ ∈ C
l,α
(Ω) u
+
∈ C
l+2,α
(Ω)
ku
+
k
C
l+2,α
(
Ω
′
)
≤ Ckρk
C
l,α
(Ω)
∀Ω
′
⊂⊂ Ω,
Γ ∈ C
l+2,α
u
+
∈ C
l+2,α
(Ω) u
−
∈ C
l+2,α
(Ω
e
)
ku
+
k
C
l+2,α
(
Ω)
≤ Ckρk
C
l,α
(Ω)
α ∈ (0, 1)
α = 0
α = 1

Ω
R
n
Γ Ω
e
≡ R
n
\Ω n
y
Γ y µ Γ
E
n
(·, y)
R
n
Γ µ u : R
n
\Γ →
R
x
u(x) =
Z
Γ
µ(y)
∂E
n
(x, y )
∂n
y
dσ
y
.
dσ
y
n = 2
y
y ∈ Γ E
n
(x, y ) x 6= y
x
∂E
n
(x, y )
∂n
y
≡ ∇
y
E
n
(x, y ) · n
y
≡
(n − 2)(x − y)
ω
n
|x − y|
n
· n
y
n ≥ 3
∂E
2
(x, y )
∂n
y
≡ ∇
y
E
2
(x, y ) · n
y
=
x − y
2π|x − y|
2
· n
y
= −
y − x
2π|x − y|
2
· n
y
n = 2 |x| → ∞ O(|x|
1−n
)
R
n
\Γ n ≥ 2
|x| → ∞ O(|x|
1−n
)
n = 3
x ∈ R
3
\ Γ
µ n
y
Γ
u(x) x Ω
Ω
e
= R
n
\Ω
u(x) =
Z
Γ
µ(y)
E
2
(x, y)
∂n
y
dσ
y
=
1
2π
Z
Γ
µ(y)
∂
∂n
y
ln
1
|x − y|
dσ
y
.
u(x) = −
1
2π
Z
Γ
µ(y)
(y − x) · n
y
|x − y|
2
dσ
y
.
Γ R
2
C
2
µ ∈ C
2
(Γ)
Γ x
0
∈ Γ
u
u(x
0
) =
1
2π
Z
Γ
µ(y)
∂
∂n
y
ln
1
|x
0
− y|
dσ
y
= −
1
2π
Z
Γ
µ(y)
(y − x
0
) · n
y
|x
0
− y|
2
dσ
y
≡
≡ −
1
2π
lim
ε→0
Z
Γ
′′
ε
(x
0
)
µ(y)
(y − x
0
) · n
y
|x
0
− y|
2
dσ
y
.
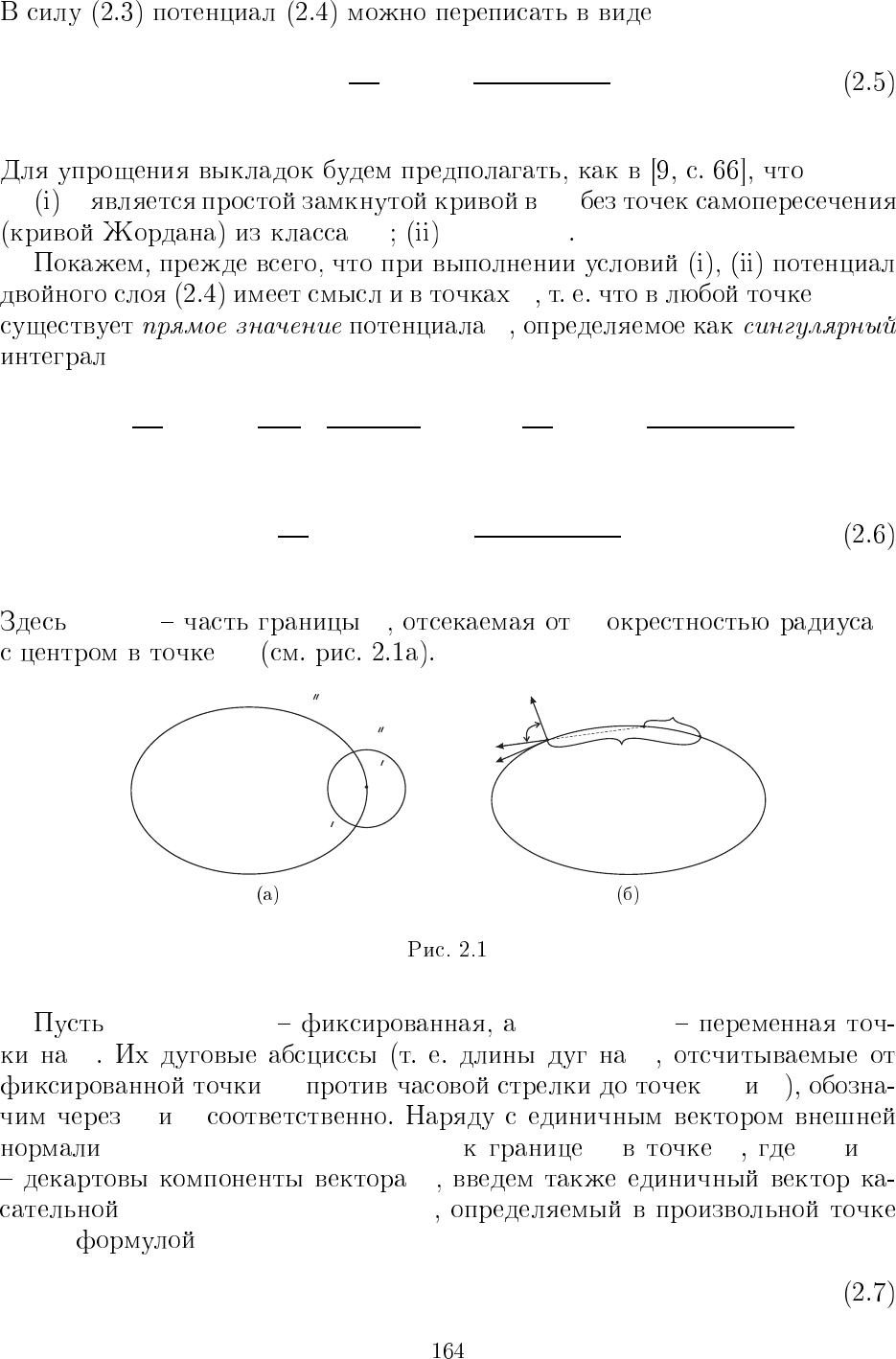
Γ
′′
ε
(x
0
) Γ Γ ε
x
0
G
G
S
S
x
0
e
e
e
e
G
j
s
s
x
y
y
t
n
y
0
0
x
0
= (x
0
1
, x
0
2
) y = (y
1
, y
2
)
Γ Γ
y
0
x
0
y
σ s
n
y
= n(y) = (n
1
(y), n
2
(y)) Γ y n
1
n
2
n
t
y
= t( y) = (t
1
(y), t
2
(y))
y ∈ Γ
t(y) = y
′
(s) = (y
′
1
(s), y
′
2
(s)), |t(y)| = |y
′
(s)| = 1.

s
n
y
t
y
n
1
(y) = t
2
(y) ≡ y
′
2
(s), n
2
(y) = −t
1
(y) ≡ −y
′
1
(s).
ϕ = ϕ( x
0
, y) ≡ ϕ(σ, s)
y − x
0
n(y) y |n
y
| = 1
cos ϕ =
(y − x
0
) · n
y
|y − x
0
|
.
Γ ∋ y →
s ∈ [0, l]
dσ
y
= |y
′
(s)|ds = ds l Γ
u[x
0
(σ)] = −
1
2π
Z
Γ
(y − x
0
) · n
y
|y − x
0
|
2
µ(y)dσ
y
= −
1
2π
Z
Γ
µ(y)
cos ϕ(x
0
, y)
|y − x
0
|
dσ
y
=
= −
1
2π
l
Z
0
µ[y(s)]
cos ϕ(σ, s)|y
′
(s)|
|y(s) − x
0
(σ)|
ds.
Γ
K : Π = [ 0, l] × [0, l] → R
K(σ, s) =
1
2π
cos ϕ(σ, s)
|y(s) − x
0
(σ)|
.
K(σ, s) σ = s
Π K
σ = s K : Π → R
Π
ψ(σ, s) = arctg
y
2
(s) − x
0
2
(σ)
y
1
(s) − x
0
1
(σ)
∂
∂s
y
2
(s) − x
0
2
(σ)
y
1
(s) − x
0
1
(σ)
=

=
y
′
2
(s)[y
1
(s) − x
0
1
(σ)] − y
′
1
(s)[y
2
(s) − x
0
2
(σ)]
[y
1
(s) − x
0
1
(σ)]
2
=
[y(s) − x
0
(σ)] · n(y)
[y
1
(s) − x
0
1
(σ)]
2
∂ψ(σ, s)
∂s
=
[y
1
(s) − x
0
1
(σ)]
2
[y
1
(s) − x
0
1
(σ)]
2
+ [y
2
(s) − x
0
2
(σ)]
2
∂
∂s
[y
2
(s) − x
0
2
(σ)]
y
1
(s) − x
0
1
(σ)
=
=
[y(s) − x
0
(σ)] · n(y)
|y(s) − x
0
(σ)|
2
=
cos ϕ(s, σ)
|y(s) − x
0
(σ)|
= 2πK(σ, s).
K
σ, s Γ
α(σ, s) =
y
2
(s) − x
0
2
(σ)
s − σ
, β(σ, s) =
y
1
(s) − x
0
1
(σ)
s − σ
,
K
K(σ, s) =
1
2π
β(σ, s)α
′
s
(σ, s) − α(σ, s)β
′
s
(σ, s)
α
2
(σ, s) + β
2
(σ, s)
.
Γ
y
1
= ξ
1
(s) y
2
= ξ
2
(s) 0 ≤ s ≤ l l
y
1
(s) − x
0
1
(σ) = (s − σ)
1
Z
0
ξ
′
1
[s + τ(σ − s)]dτ,
y
2
(s) − x
0
2
(σ) = (s − σ)
1
Z
0
ξ
′
2
[s + τ(σ − s)]dτ.
lim
s→σ
K(σ, s) =
1
2π
x
0
2
′
(σ)x
0
1
′′
(σ) − x
0
1
′
(σ)x
0
2
′′
(σ)
(x
0
1
′
)
2
+ (x
0
2
′
)
2
=
æ(σ)
2π
.
æ(σ) Γ σ ∈ Γ
æ(σ) =
x
0
2
′
(σ)x
0
1
′′
(σ) − x
0
1
′
(σ)x
0
2
′′
(σ)
(x
0
1
′
)
2
+ (x
0
2
′
)
2
Γ
K(σ, s) s = σ K(σ, σ) =

æ(σ)/2π α β α
′
s
β
′
s
σ s α
2
+ β
2
6= 0 ∀σ, s
K
s σ Γ
K Γ
x
0
σ Γ
(i) (ii)
Γ
µ ∈ C
2
(Γ)
µ ∈ C(Γ) µ Γ
B
ε
(x
0
) ε x
0
∈ Γ
Γ
′
ε
Γ Ω B
ε
, B
′
ε
= B
ε
(x
0
) ∩ Ω
B
′′
ε
= B
ε
\ B
′
ε
v C
2
(B
ε
)
v(y) = µ(y),
∂v(y)
∂n
y
= 0, y ∈ Γ
′
ε
.
µ ∈ C
2
(Γ)
S
′
ε
S
ε
≡ S
ε
(x
0
) = {x ∈ R
2
:
|x − x
0
| = ε}
Ω
x 6∈ B
′
ε
2
X
i=1
∂
∂y
i
ln|x − y|
∂v(y)
∂y
i
− v(y)
∂
∂y
i
ln|x − y|
=
= ln|x − y|∆
y
v(y) − v(y)∆
y
ln|x − y|
B
′
ε
∆
y
ln|x−y| = 0 B
′
ε
x 6∈ B
′
ε
Z
Γ
′
ε
∪S
′
ε
ln|x − y|
∂v(y)
∂n
y
− v( y)
∂ln|x − y |
∂n
y
dσ
y
=
=
Z
B
′
ε
ln|x − y|∆
y
v(y)dy ∀x ∈ B
′′
ε
(x
0
).

Γ
′
ε
−
Z
Γ
′
ε
µ(y)
∂ln|x − y |
∂n
y
dσ
y
+
Z
S
′
ε
ln|x − y|
∂v(y)
∂n
y
− v(y)
∂
∂n
y
ln|x − y|
dσ
y
=
=
Z
B
′
ε
ln|x − y|∆
y
v(y)dy ∀x ∈ B
′′
ε
(x
0
).
x ∈ B
′
ε
∪ Γ
′
ε
B
′
ε
∪ Γ
′
ε
x B
δ
(x)
δ x
δ
C
2
R
2
−
Z
Γ
′
ε
µ(y)
∂ln|x − y|
∂n
y
dσ
y
+
Z
S
′
ε
ln|x − y|
∂v(y)
∂n
y
− v( y)
∂
∂n
y
ln|x − y|
dσ
y
+
+q(x)v(x) =
Z
B
′
ε
ln|x − y|∆
y
v(y)dy ∀x ∈
B
′
ε
(x
0
).
q(x) = 2π x ∈ B
′
ε
(x
0
) q(x) = π x ∈ Γ
′
ε
x B
ε
q
q(x) =
2π, x ∈ B
′
ε
,
π, x ∈ Γ
′
ε
,
0, x ∈ B
′′
ε
.
Γ
′′
ε
= Γ\Γ
′
ε
x
0
B
ε/2
(x
0
)
u(x) = −
1
2π
Z
Γ
′′
ε
µ(y)
∂
∂n
y
ln|x−y|dσ
y
−
1
2π
Z
Γ
′
ε
µ(y)
∂
∂n
y
ln|x−y |dσ
y
, x ∈ B
ε
(x
0
).
x ∈ B
ε
(x
0
)
Γ
2π
u(x) = −
1
2π
Z
Γ
′′
ε
µ(y)
∂
∂n
y
ln|x − y|dσ
y
−

1
2π
Z
S
′
ε
v(y)
∂
∂n
y
ln|x − y| − ln|x − y|
∂v(y)
∂n
y
dσ
y
+
+
1
2π
Z
B
′
ε
ln|x − y|∆v(y) dy −
1
2π
q(x)v(x), x ∈ B
ε
(x
0
).
x
0
x
0
B
ε/2
(x
0
) ε/2
(B
′
ε
, ∆v) v
R
2
x x
0
v ∈ C
2
(B
ε
) q
q
B
′
ε
Γ
′
ε
B
′′
ε
B
ε
qv
u Γ
x
0
x
0
Γ
(i), ( ii)
u(x
0
) : Γ → R
x
0
∈ Γ C
1
(Γ)
qv
Γ x
Ω Ω
e
x
0
u(x
0
), u
+
(x
0
) = lim
x→x
0
x∈Ω
u(x), u
−
(x
0
) = lim
x→x
0
x∈Ω
e
u(x)
u
+
(x
0
) − u(x
0
) = −
1
2
µ(x
0
), u
−
(x
0
) − u(x
0
) =
1
2
µ(x
0
),
u
+
(x
0
) − u
−
(x
0
) = −µ(x
0
).

x Ω Ω
e
x
0
q Ω Ω
e
v
lim
x→x
0
x∈Ω
∂u(x)
∂n
x
=
∂u
+
(x
0
)
∂n
x
0
, lim
x→x
0
x∈Ω
e
∂u(x)
∂n
x
=
∂u
−
(x
0
)
∂n
x
0
,
∂u
−
(x
0
)
∂n
x
0
=
∂u
+
(x
0
)
∂n
x
0
∀x
0
∈ Γ.
x Γ
x
0
∈ Γ
µ ∈ C(Γ)
Γ
Γ µ
u : R
n
\ Γ → R
u(x) =
Z
Γ
E
n
(x, y)µ(y)dσ
y
, x ∈ R
n
\ Γ.
E
n
u R
n
\ Γ
n ≥ 3 u |x| → ∞
O(|x|
2−n
) n = 2
u(x) =
1
2π
Z
Γ
ln
1
|x − y|
µ(y)dσ
y
u(x) = −
ln|x|
2π
Z
Γ
µ(y)dσ
y
+
1
2π
Z
Γ
ln
|x|
|x − y|
µ(y)dσ
y
.
R
2
|x| → ∞
