Alciatore D.G., Histand M.B. Introduction to Mechatronics and Measurement Systems
Подождите немного. Документ загружается.


Confirming Pages
Figure 4.3 Squa re wave.
f (t)
t
1
T
4.3 Fo urier Series Representation of Signals 121
In the Fourier series representation given by Equation 4.3, there are two differ-
ent amplitudes (A
n
and B
n
). However, the cosine and sine terms can be combined
with a trigonometric identity (Question 4.4) to create an alternative representation
described by a single amplitude and phase. This alternative representation is
F
(4.7)
where the total amplitude for each harmonic is given by
C
n
A
n
2
B
n
2
+=
(4.8)
and the phase for each harmonic is given by
φ
n
B
n
A
n
-----
⎝⎠
⎛⎞
tan
1–
–=
(4.9)
To illustrate the application and meaning of a Fourier series, consider an ideal
square wave as an example of a periodic waveform. The square wave illustrated in
Figure 4.3 is defined mathematically as
ft()
1 0 t≤ T 2⁄<
1– T 2⁄ tT<≤
⎩
⎨
⎧
=
(4.10)
where T is the period. There are discontinuities at t 0 and T 2.
For the square wave defined by Equation 4.10, the coefficients A
n
, including A
0
,
are 0 (see Question 4.5). The coefficients B
n
can be found from Equation 4.5 :
B
n
2
T
−
nω
0
t()sin td
0
T 2
⁄
∫
nω
0
t()sin td
T 2
⁄
T
∫
–=
(
(4.11)
Integration results in
B
n
2
T
---
1
nω
0
---------
– nω
0
t()cos[]
0
T 2⁄
1
nω
0
---------
nω
0
t()cos[]
T 2⁄
T
+
⎝⎠
⎛⎞
=
(4.12)
alc80237_ch04_117-160.indd 121alc80237_ch04_117-160.indd 121 1/4/11 3:48 PM1/4/11 3:48 PM

Confirming Pages
Figure 4.4 Harmoni c decomposition of a square wave.
individual harmonics combined harmonics
ω
0
3ω
0
5ω
0
ω
0
ω
0
, 3ω
0
ω
0
, 3ω
0
, 5ω
0
amp = 4/π
amp = 4/(3π)
amp = 4/(5π)
amp = 0
∞ω
0
ω
0
, 3ω
0
, 5ω
0
, . . . , ∞ω
0
122 CHAPTER 4 System Response
Using Equation 4.2 in evaluating the bracketed terms at each of the limits in Equation
4.12 gives
B
n
1
nπ
------
nπ()11 nπ()cos–++cos–{}=
(4.13)
This can be written as
B
n
2
nπ
------
1 nπ()cos–[]
4
nπ
------
n:odd
0 n:even
⎩
⎪
⎨
⎪
⎧
==
(4.14)
Therefore, the Fourier series representation of a square wave of amplitude 1 is
Ft()
4
π
---
ω
0
t()sin +
4
3π
------
3ω
0
t()sin +
4
5π
------
5ω
0
t()· · · +sin=
(4.15)
or , using an infinite sum representation,
Ft()
4
2n 1–()π
−−−−−−−−−−
2n 1–()ω
0
t[]sin
n 1
=
∞
∑
=
(4.16)
Fi gure 4.4 shows the effects of combining the individual harmonics of the sig-
nal incrementally. MathCAD Example 4.1 includes the analysis used to create the
figure. Shown on the left side of the figure are the individual harmonics along with
their frequencies and amplitudes. Note that, as the harmonic frequency increases,
the amplitudes of the harmonics decrease. Illustrated on the right are the superposi-
tions of the successive harmonics, illustrating how the addition of higher harmonics
improves the representation of the square wave. If we take the first, third, and fifth
harmonics and add them together, we obtain a waveform that begins to look similar
to a square wave. As we add additional harmonics to this signal, the quality of the
reproduction of the waveform improves and sharp changes are better approximated.
If an infinite number of harmonics were used, the result would be a square wave.
MathCAD Example
4.1Fourier series
representation of a
square wave
alc80237_ch04_117-160.indd 122alc80237_ch04_117-160.indd 122 1/4/11 3:48 PM1/4/11 3:48 PM

Confirming Pages
Figure 4.5 Spectrum of a square wave.
signal
spectrum
time
frequency
amplitude
DC offset
0
ω
0
3ω
0
5ω
0
7ω
0
9ω
0
11ω
0
DC component
0
1.5
2.5
0.5
1.5
4/π
4/(3π)
13
ω
0
time
domain
frequency
domain
4.3 Fo urier Series Representation of Signals 123
Waveforms such as a square wave, which have very sharp or rapid changes associ-
ated with them (e.g., at discontinuities), require a large number of higher harmonics
for good reproduction.
The top half of Figure 4.5 illustrates a plot of a unity amplitude square wave
with a DC offset of 1.5. This plot is known as the time-do main representation of the
signal. The bottom half of the figure is a plot of the Fourier series amplitudes vs. fre-
quency, which is called the signal’s spectrum. Since the harmonics are represented
as bars or lines on the graph, it is also called a line spectrum. Note that the DC offset
is the zero frequency component. The spectrum is the signal’s frequency-domain
representation.
When plotting the spectrum for a signal represented by a Fourier series, one
should use the single-amplitude version given by Equation 4.7. For the square
wave Fourier series given in Equation 4.15, the A
n
coefficients are 0, and the C
n
coefficients are the same as the B
n
coefficients (see Equation 4.8). Each bar in
Figure 4.5 represents a different amplitude value. The first bar represents a
DC offset of C
0
= B
0
= 1.5. The second bar represents the first term in Equation
4.15: C
1
= B
1
= 4/. The remaining bars represent the higher nonzero harmonics
(B
3
, B
5
, . . .).
Video Demo 4.1 shows spectra for various output signals from a function gen-
erator. A digital oscilloscope makes it very easy to display the spectrum of any elec-
trical signal. Observe how signals with fast transitions (e.g., sharp corners) contain
larger amplitude harmonics at higher frequencies.
Internet Link 4.1 provides various resources and demonstrations relating to how
signal spectrum concepts can be applied to sound and music theory. Sound consists
of pressure waves. A microphone can acquire a pressure signal and convert it into
a voltage signal that can be processed and displayed (e.g., on an oscilloscope). The
spectral content of different sounds is what differentiates the characters (timbres) of
sound (see Class Discussion Item 4.1). Furthermore, a musical note (i.e., its pitch)
is defined by its fundamental frequency and its signal amplitude determines its vol-
ume (i.e., loudness). Video Demos 4.2 through 4.7 show different examples of these
concepts.
Video Demo
4.1Sine-wave,
saw-tooth-wave,
and square-wave
signal spectra
4.2Spectra of
whistling and
humming, and
amplifier saturation
4.3Bugle tone
amplitude, fre-
quency, and
spectra
4.4Guitar
harmonics and
chords
4.5Piano
harmonics and
tone spectra
4.6Piano
keyboard har-
monics and
chords
4.7Tuning fork
waveform analysis
Internet Lin
k
4.1Video
demonstrations
and online
resources for
sound and
vibration
principles
alc80237_ch04_117-160.indd 123alc80237_ch04_117-160.indd 123 1/4/11 3:48 PM1/4/11 3:48 PM
Confirming Pages
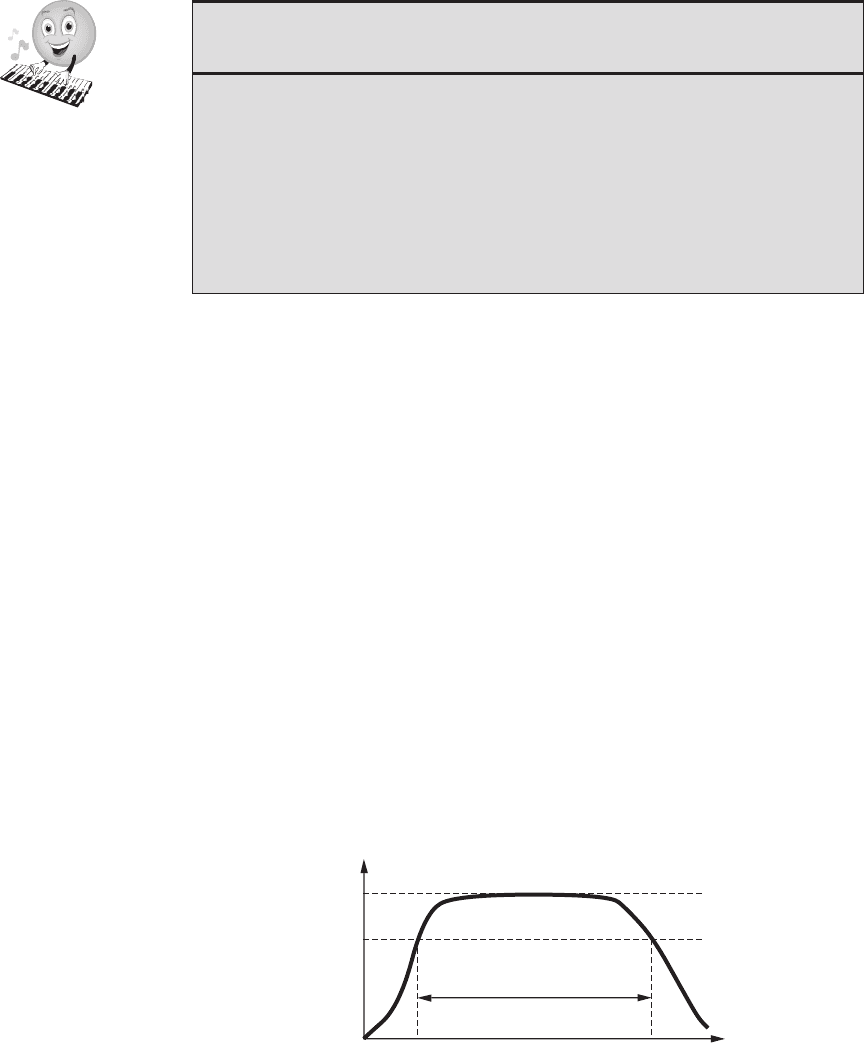
Figure 4.6 Frequency response and bandwidth.
1.000
0.707
(–3 dB)
bandwidth
frequency
amplitude ratio (A
out
/A
in
)
ω
L
ω
H
124 CHAPTER 4 System Response
■ CLASS DISCUSSION ITEM 4.1
Musical Harmonics
Using your knowledge of harmonics, explain each of the following musical phenomena:
■ Why does a C on a flute sound different from the same C on a violin?
■ Guitar players achieve an effect called harmonics by lightly placing a finger on
the midpoint of a string before picking. Explain why this changes the quality of
the sound produced.
■ When striking middle C on a piano while holding the damper pedal down
(allowing all strings to ring freely), why do strings other than middle C begin to
vibrate? Which strings vibrate with the largest amplitude?
4.4 BANDWIDTH AND FREQUENCY
RESPONSE
It is important to estimate the spectrum of a signal when choosing a system to measure
the signal. Ideally, a measurement system should replicate all frequency components
of a signal. Real systems, however, have limitations in their ability to reproduce all
frequencies. A scale commonly used to measure the degree of fidelity of a measure-
ment system’s reproduction at different frequencies is the decibel scale. It is a loga-
rithmic scale that allows comparison of the change in amplitude of a component of a
signal when it passes through a measurement system. The decibel (dB) is defined as
dB 20 log
10
A
out
A
in
--------
⎝⎠
⎛⎞
=
(4.17)
where A
in
is the input amplitude and A
out
is the output amplitude of a particular
harmonic.
The graph shown in Figure 4.6 is an example of a frequency response curve for
a system. This graph is also called a Bode plot. It is a plot of the amplitude ratio,
A
out
A
in
, vs. the input frequency. It characterizes how com ponents of an input signal
are amplified or attenuated by the system. The term bandwidth is used to quantify
alc80237_ch04_117-160.indd 124alc80237_ch04_117-160.indd 124 1/4/11 3:48 PM1/4/11 3:48 PM

Confirming Pages
4.4 Bandwidth and Frequency Response 125
the range of frequencies a system can adequately reproduce. The bandwidth of a
system is defined as the range of frequencies where the input of the system is not
attenuated by more than −3 dB. As illustrated in the figure, a system usually has
two frequencies at which the attenuation of the system is −3 dB. They are defined
as the low and high corner or cutoff frequencies
L
and
H
. These two frequencies
define the bandwidth of the system:
b
an
d
w
id
t
h
=ω
L
to ω
H
(4.18)
Measurement systems often exhibit no attenuation at low frequencies (i.e.,
L
= 0),
and the amplitude ratio degrades only at high frequencies. For these systems, the
bandwidth extends from 0 (DC) to
H
.
The −3 dB cutoff is the decibel value when the power of the output signal (P
out
)
is attenuated to half of its input value (P
in
):
P
out
P
in
--------
1
2
-- -
=
(4.19)
For this reason, the cutoff frequencies are referred to as the half-power points. The
power of a sinusoidal signal is proportional to the square of the signal’s amplitude,
thus at the cutoff value,
A
out
A
in
--------
P
out
P
in
--------
1
2
-- - 0.70
7
≈==
(4.20)
Therefore, at the cutoff frequencies, the amplitude of the signal is attenuated by
29.3% (to 70.7% of its original value), which is approximately −3 dB:
dB = 20 log
10
1
2
-- - 3– dB≈
(4.21)
At first it may seem illogical to define the bandwidth to exclude signal com-
ponents that exist outside the range of the bandwidth. The half-power points are
admittedly somewhat arbitrary, but if applied consistently, they allow us to compare
a variety of instruments and system responses. All signal amplitudes of components
outside the bandwidth are attenuated by more than 3 dB. Components that lie within
the bandwidth, especially those close to the cutoff frequencies, may also be attenu-
ated but by less than 3 dB.
The frequency response of an ideal measurement system has an amplitude ratio
of 1, extending from 0 to infinite frequency. An ideal system reproduces all har-
monics in a signal without amplification or attenuation. A real measurement system,
however, has a limited bandwidth. The bandwidth of a system is influenced by such
factors as capacitance, inductance, and resistance in electrical systems and mass,
stiffness, and damping in mechanical systems. Through careful design, these param-
eters can be selected to achieve a desired bandwidth. A properly designed measure-
ment system reproduces all frequency components in a typical input signal. When it
does, the system is said to exhibit high fidelity.
The proper design or selection of a measurement system requires an understand-
ing of measurement system bandwidth and signal spectrum. Figure 4.7 illustrates an
alc80237_ch04_117-160.indd 125alc80237_ch04_117-160.indd 125 1/4/11 3:48 PM1/4/11 3:48 PM

Confirming Pages
126 CHAPTER 4 System Response
input signal spectrum, a measurement system’s frequency response, and the resulting
spectrum of the output signal, all using the same frequency scale. The measurement
system has a limited bandwidth, so not all input signal frequency components are
reproduced satisfactorily. Therefore, the output signal differs from the input signal.
Given the input signal spectrum in the figure, the signal can be written as
V
in
(t) = A
1
sin(ω
0
t) + A
2
sin(2ω
0
t) + A
3
sin(3ω
0
t) + · · ·
(4.22)
Given the measurement system frequency response curve, the output amplitude A
i
can
be determined for each input frequency amplitude A
i
using the following equation:
= (A
out
⁄ A
in
)
i
× A
i
A
i
'
(4.23)
■ CLASS DISCUSSION ITEM 4.2
Measuring a Square Wave with a Limited Bandwidth System
Assume you have a measurement system whose bandwidth is 0 to 5.1
0
, with no
attenuation below the cutoff frequency and complete attenuation above. If the input
to the system is a square wave with a fundamental frequency of
0
, describe the dif-
ference between the input and the output.
Figure 4.7 Effect of mea surement system bandwidth
on signal spectrum.
input signal spectrum
output signal
spectrum
A
in
frequency
A
out
measurement system
frequency response
A
out
/A
in
frequency
frequency
1
0.5
A
3
A
2
A
3
0.25 A
2
A
1
0.25
ω
0
2ω
0
3ω
0
10ω
0
'
alc80237_ch04_117-160.indd 126alc80237_ch04_117-160.indd 126 1/4/11 3:48 PM1/4/11 3:48 PM
Confirming Pages
4.4 Bandwidth and Frequency Response 127
where i is the frequency component number. For example, for i = 2 corresponding to
frequency 2
0
,
= (A
out
⁄ A
in
)
2
× A
2
= 0.25A
2
A'
2
(4.24)
Applying Equation 4.23 to each frequency component results in the spectrum shown
at the bottom of the figure, and the output signal can be written as
(4.25)
or
(4.26)
Because A
out
/ A
in
= 1 for all frequencies between and including 3
0
and 9
0
, A
i
A
i
for i = 3 through 9. Because A
out
/ A
in
0 for the frequency component ω
0
and for all
components above 10ω
0
, these components are completely attenuated and no longer
exist in the output signal (i.e., A
1
A
11
A
12
. . . 0). The frequency compo-
nents at 2ω
0
and 10ω
0
still exist in the output signal, but their amplitudes are partially
attenuated (0 < A
out
/ A
in
< 1).
When designing or choosing a measurement system for an application, it is
important that the bandwidth of the system be large enough to adequately reproduce
the important frequency components present in the input signal. A measurement sys-
tem that does not reproduce high frequencies cannot accurately reproduce signals
that have rapid changes associated with them.
To experimentally determine the bandwidth of a system, it is necessary to
systematically apply pure sinusoidal inputs and to determine the output-to-input
amplitude ratio for the desired range of frequencies. The sweep feature on a func-
tion generator, which generates a linearly increasing frequency over a selected time,
provides a convenient method to perform this for systems with electrical inputs. Lab
Exercise 4 applies this technique to filter circuits (see the demonstration in Video
Demo 4.8). A method for theoretically determining the frequency response of a sys-
tem model is presented in Section 4.10.2. Example 4.1 illustrates the basics of the
technique, applied to a simple RC filter.
V
out
(t) = sin(2ω
0
t) + sin(3ω
0
t) + · · · + sin(9ω
0
t) + sin(10ω
0
t
)
A'
2
A'
3
A'
9
A'
10
V
out
(t) = 0.25A
2
sin(2ω
0
t) + A
3
sin(3ω
0
t) + · · · + A
9
sin(9ω
0
t) + 0.5A
10
sin(10ω
0
t)
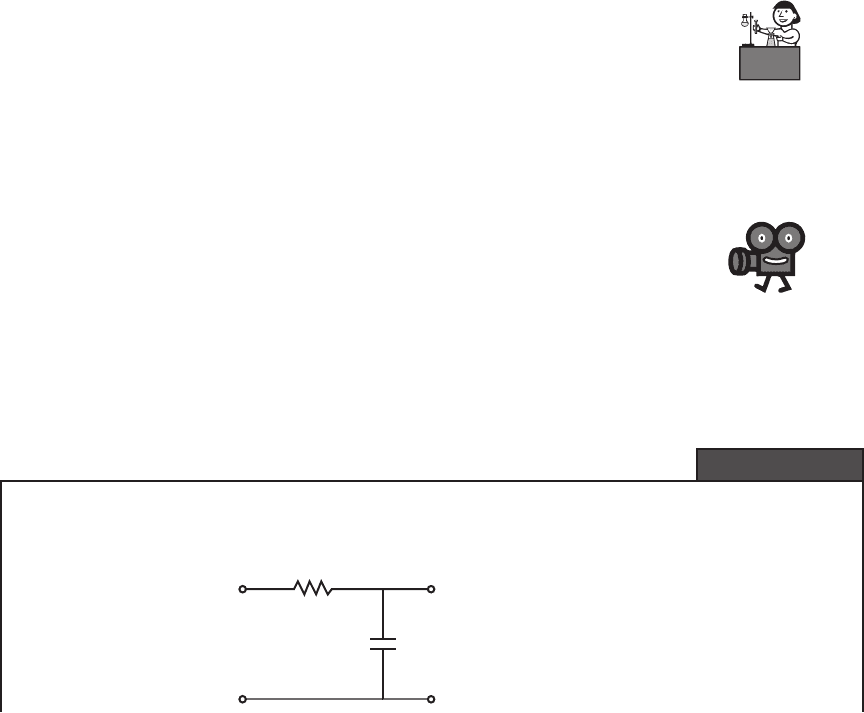
Bandwidth of an Electrical Network
EXAMPLE 4.1
The bandwidth of an electrical system can be readily determined analytically with the help
of the steady state AC circuit analysis technique presented in Section 2.6. Consider the fol-
lowing RC circuit as an example.
V
in
V
ou
t
R
C
+
+
–
–
(continued )
'
'
'
'
Lab Exercise
Lab 4Band-
width, filters, and
diodes
Video Demo
4.8Filter (RC
circuit) frequency
response
alc80237_ch04_117-160.indd 127alc80237_ch04_117-160.indd 127 1/4/11 3:48 PM1/4/11 3:48 PM

Confirming Pages
128 CHAPTER 4 System Response
(continued )
Using the voltage divider rule for the complex impedances of the resistor (Z
R
R) and
capacitor (Z
C
1/jC), the output voltage for the network can be written as
V
out
1
jωC
----------
1
jωC
----------
R+
--------------------
V
in
=
Therefore, the output-to-input ratio as a function of frequency is
V
out
V
in
-
-------- -
1
jωRC 1+
-----------------------
=
The magnitude of this complex number gives us the amplitude ratio as a function of frequency:
V
out
V
in
--------- -
1
1 ωRC()
2
+
---------------------------------
=
The cutoff frequency ω
c
for the circuit is
ω
c
1
RC
------- -
=
because
V
out
V
in
--------- -
1
2
-------
0.707==
when =
c
.
Using
c
, the amplitude ratio can also be expressed as
V
out
V
in
--------- -
1
1 ωω
c
⁄()
2
+
-----------------------------------
=
The frequency response curve representing this relationship follows, where
r
/
c
and A
r
|V
out
/V
in
|. Note that, as
r
approaches 0, A
r
approaches 1 and as
r
approaches , A
r
approaches 0. MathCAD Example 4.2 includes the analysis used to generate the frequency
response plot.
This circuit is called a low-pass filter because lower frequencies are “passed” to the output
with little attenuation and higher frequencies are significantly attenuated (i.e., not “passed”).
r
:= 0, 0.01 . . 2.5
0 0.5 1 1.5 2 2.5
0.2
0.4
0.6
0.8
1
0.707
A
r
(ω
r
)
1
ω
r
A
r
ω
r
() :=
1
1 ω
r
2
+
-------------------
MathCAD Example
4.2Low-pass filter
alc80237_ch04_117-160.indd 128alc80237_ch04_117-160.indd 128 1/4/11 3:48 PM1/4/11 3:48 PM

Confirming Pages
4.5 Phase Linearity 129
If the resistor and capacitor were reversed, the resulting circuit would be called a high-
pass filter because it would attenuate low frequencies. Two other useful filters are the notch
filter and band-pass filter. The notch filter, sometimes called the band-reject filter, passes
all frequencies except for a narrow band of frequencies that are highly attenuated. A com-
mon use for this filter is to eliminate 60 Hz interference often found on signal lines. The
band-pass filter, on the other hand, passes a narrow band of frequencies and significantly
attenuates all others.
4.5 PHASE LINEARITY
The third criterion for a good measurement system is phase linearity, which expresses
how well a system preserves the phase relationship between frequency components
of the input.
Consider the relationship between phase angle and time displacement between
two signals as illustrated in Figure 4.8. Signal 2 lags signal 1 because it occurs later
on the time axis. The time displacement between the signals t
d
is T /4, where T is the
period of the signals. Since a cycle of a signal corresponds to 2π radians or 360, the
phase angle between signal 1 and signal 2 is
φ
= 3
6
0 t
d
⁄ T
d
egrees = 2π t
d
⁄ T ra
di
ans
(4.27)
So for t
d
T /4, the phase angle is 90 or π /2 radians.
Measurement systems can cause a delay or time displacement between the input
and output signals. For a given frequency f, where f = 1 /T, Equation 4.27 can be
expressed as
φ = 360
f · t
d
degrees = 2πf · t
d
radians
(4.28)
Therefore, for a given time displacement, the phase shift for a signal depends on
its frequency. Since an input signal may be composed of many frequency compo-
nents, it is important that all the individual components are displaced by the same
amount of time; otherwise, the output of the measurement system would be dis-
torted. For equal time displacement t
d
for all frequency components, the following
must hold:
φ = k · f
(4.29)
Figure 4.8 Relationship be tween phase and time displacement.
signal 1: sin(ωt)
signal 2: sin(ωt – φ)
t
t
d
= T/4
alc80237_ch04_117-160.indd 129alc80237_ch04_117-160.indd 129 1/4/11 3:48 PM1/4/11 3:48 PM

Confirming Pages
Figure 4.9 Amplitude distor tion of a square wave (generated with MathCAD).
t := 0, 0.01 . . 2 n := 1 . . 50
B
n
:=
4
π 2 n 1–⋅()⋅
--------------------------------
exp 0.1–2n 1–()[]C
n
:=
4
π 2n 1–()
-----------------------
1exp 2n 1–()–[]–{}
F
high
t() := B
n
2n 1–()2πt[]sin
n
∑
F
low
t() := C
n
2n 1–()2πt[]sin
n
∑
0 1 2
0
F
high
(t)
t
012
0
F
low
(t)
t
(a) high-frequency components attenuated
(b) low-frequency components attenuated
130 CHAPTER 4 System Response
where k is a constant equal to 360t
d
degrees or 2πt
d
radians. Therefore, the phase
angle must be linear with frequency for equal time displacement of frequency com-
ponents. When a system functions in this way, it is said to exhibit phase linearity.
k is usually negative for a measurement system, implying that the recorded output
lags behind the actual input signal.
4.6 DISTORTION OF S IGNALS
When a system does not exhibit amplitude linearity, the amplitudes of the out-
put frequency components are attenuated. As a result, the output suffers from
amplitude distortion as illustrated in Figure 4.9 for a square wave. In the figure,
the coefficients of the harmonics contain exponential functions whose magnitudes
decrease (a) or increase (b) with frequency. Note the change (distortion) in the result-
ing outputs. MathCAD Example 4.3 includes the analysis used to create the plots in
Figure 4.9.
When a system does not exhibit phase linearity, the output frequency compo-
nents may be of the proper amplitude but are displaced in time with respect to one
another. As a result, the output exhibits phase distortion as illustrated in Figure 4.10
for a square wave. MathCAD Example 4.4 includes the analysis used to create the
plots in Figure 4.10.
A high-fidelity measurement system must exhibit amplitude linearity to pre-
vent amplitude distortion, have adequate bandwidth to pass all frequency compo-
nents contained in an input signal, and exhibit phase linearity to prevent phase
distortion.
When designing or analyzing a measurement system, we want to predict the sys-
tem’s performance. Therefore, we need to be able to model the system and express
its behavior in mathematical terms. The remainder of the chapter presents systems
analysis tools that let us do this.
MathCAD Example
4.3Amplitude
distortion
4.4Phase
distortion
alc80237_ch04_117-160.indd 130alc80237_ch04_117-160.indd 130 1/4/11 3:48 PM1/4/11 3:48 PM
