Alciatore D.G., Histand M.B. Introduction to Mechatronics and Measurement Systems
Подождите немного. Документ загружается.

Confirming Pages
Questions and Exercises 111
+
+
–
R
R
V
in
V
out
(e)
+
+
–
V
in
V
ou
t
(f)
3.3. Document a complete and thorough answer to Class Discussion Item 3.1.
3.4. Document a complete and thorough answer to Class Discussion Item 3.2.
3.5. Document a complete and thorough answer to Class Discussion Item 3.3.
3.6. Sketch the output waveform for V
out
in the following circuit on axes as shown.
Assume ideal diodes and show your work. Also, explain why this circuit is called a
full-wave rectifier.
1
–1
volts
0
V
out
3 s21
+
sin(πt)
+–
1 kΩ
V
out
3.7. Document a complete and thorough answer to Class Discussion Item 3.5.
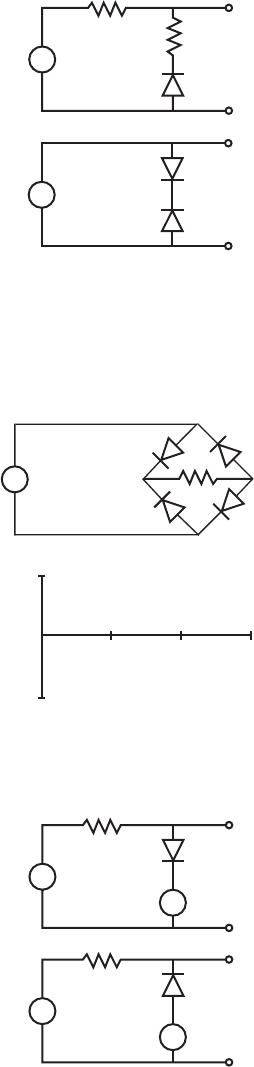
3.8. The following circuits are called clipping circuits. Assume ideal diodes and sketch
the output voltage V
out
for two cycles of the input V
in
.
1 k
0.5 V
Ω
+
+
+
–
V
in
= sin(2πt) V
out
(a)
1 k
0.5 V
Ω
+
+
+
–
V
in
= sin(2πt) V
out
(b)
alc80237_ch03_073-116.indd 111alc80237_ch03_073-116.indd 111 1/3/11 3:47 PM1/3/11 3:47 PM
Confirming Pages
112 CHAPTER 3 Semiconductor Electronics
3.9. Compute the currents ( I
1
, I
2
, I
3
, I
4
) and the diode voltage ( V
diode
) in the final circuit
shown in Example 3.3.
3.10. In Example 3.3, for the case where both diodes are assumed to be reverse biased,
find I
1
, I
4
, and V
AB
(the voltage of node A relative to node B) in the assumed-polarity
circuit. Based on voltage V
AB
, for which diode was the polarity assumption correct?
3.11. Document a complete and thorough answer to Class Discussion Item 3.7.
3.12. For the following circuit, assuming ideal diodes and given R 1 kΩ and
V
in
10 sin( t ) V, plot the output voltage V
out
on axes with labeled scales for two
periods of the input.
+
–
R
R
+
V
in
V
out
3.13. For the following circuit, find the steady state values for V
out
, the voltage across and
current into the capacitor, and the current through the output resistor for
a. V
s
10 V DC
b . V
s
10 V DC
R
R
C
+
+
–
R
V
s
R
c
= 2R
V
out
3.14. For Class Discussion Item 3.7 with V
in
15 sin(2 t ) V and R
i
R
L
1 kΩ, draw
and label one cycle of V
in
and V
out
. Assume ideal diodes.
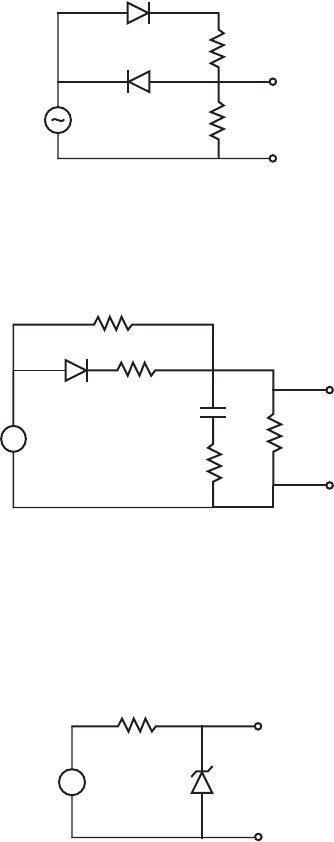
3.15. Given the following ideal zener diode circuit with breakdown voltage 5.1 V, sketch
the output voltage on a set of axes if
a. V
in
1.0 sin(2 t )
b . V
in
10.0 sin(2 t )
+
–
V
out
1 kΩ
V
in
+
alc80237_ch03_073-116.indd 112alc80237_ch03_073-116.indd 112 1/3/11 3:47 PM1/3/11 3:47 PM
Confirming Pages
Questions and Exercises 113
3.16. A digital circuit can output a voltage of either 0 V or 5 V relative to ground. Design a
circuit that uses this output to turn an LED on or off assuming the LED
a. has no forward voltage drop and can carry a maximum of 50 mA
b. has a forward voltage drop of 2 V and can carry a maximum of 50 mA
Section 3.4 Bipolar Junction Transistor
3.17. In the following circuit, what minimum steady state voltage V
in
is required to turn the
LED on and keep the transistor fully saturated? Assume that the forward bias voltage
for the LED is 2 V and there is a 0.2 V collector-to-emitter voltage drop when the
transistor is saturated.
V
in
5 V
LED
330 Ω
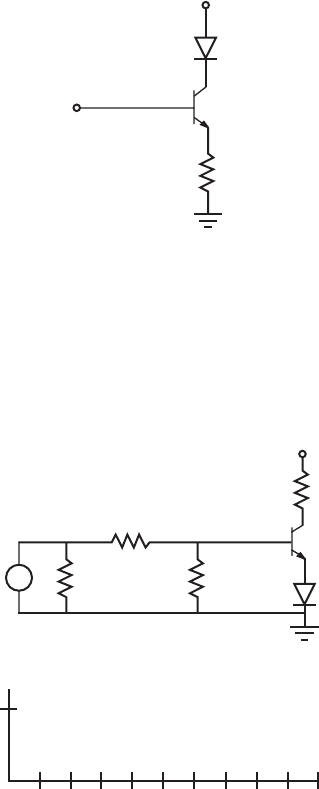
3.18.
a. Given V
in
(see the graph that follows) for the following circuit, and assuming the
current into the base of the transistor is very small (i.e., assume I
B
0), sketch
the LED on-off curve on a graph similar to that shown below the circuit. Assume
that the LED has a forward bias voltage of 1 V. Also assume the transistor is in
saturation when the LED is on.
b. Calculate the minimum value of V
in
required to saturate the transistor assuming a
beta of 100. Don’t assume I
B
0 in this part.
+
V
in
1 kΩ
1 kΩ
1 kΩ
330 Ω
LED
5 V
t
1
2
345
OFF
ON
LED
alc80237_ch03_073-116.indd 113alc80237_ch03_073-116.indd 113 1/3/11 3:47 PM1/3/11 3:47 PM
Confirming Pages
114 CHAPTER 3 Semiconductor Electronics
V
in
(V)
t
2
4
6
–2
–4
–6
12 34 5
3.19. In the following circuit, find the minimum V
in
required and the resulting voltage V
out
to put the transistor in full saturation. Assume that the beta for the transistor is 100 in
full saturation.
+
R
B
= 1kΩ
R
out
= 1kΩ
R
C
= 1kΩ
V
S
= 5 V
V
ou
t
V
in
3.20. Consider the design of a solid state switch using an npn power transistor that you
plan to control with a digital signal (0 V off, 5 V on). Start with the following
schematic where components that you must select are labeled with numbers. The
series resistor and inductor represents a DC motor that requires 1 A of current at
24
V
DC
. Replace each of the labeled boxes shown in the figure with the appropriate
schematic symbol and then specify the component as completely as you can.
4
10
5 V
2
3
3.21. A photo-interrupter comes in a manufactured package that includes the phototransis-
tor and corresponding LED as shown in the following schematic. What external cir-
cuitry must be added to obtain a functioning photo-interrupter? Sketch the resulting
schematic.
alc80237_ch03_073-116.indd 114alc80237_ch03_073-116.indd 114 1/3/11 3:47 PM1/3/11 3:47 PM

Confirming Pages
Questions and Exercises 115
Section 3.5 Field-Effect Transistors
3.22. For the MOSFET used in the experiment of Figure 3.31 , estimate the fully-on drain-
to-source resistance R
on
from the values in the plot.
3.23. Answer Question 3.20 using an n-channel enhancement-mode power MOSFET
instead of the npn BJT.
3.24. In Design Example 3.4, suppose V
s
15 V. Replace the MOSFET with a BJT power
transistor and specify the type (npn or pnp) and any additional components required.
Draw the circuit schematic and describe its characteristics.
3.25. The output of most digital CMOS devices looks like this:
V
in
V
cc
V
out
Identify the types of MOSFETs used. What is the value of V
out
for V
in
5 V and for
V
in
0 V?
3.26. The following table lists various MOSFETs available for a design project. You have
a requirement to switch 10 A at 10 V. Select the MOSFET adequate for the require-
ments and defend your choice.
MOSFET
V
ds
(V) R
ds
(on) (Ω) I
d
cont (A) @ 25°C P
d
(max) (W)
IRF510 100 0.6 16 20
IRF530N 100 0.11 60 63
IRF540 100 0.077 110 150
IRF540N 100 0.052 110 94
IRF610 200 1.5 10 20
3.27. For each state of an n-channel enhancement-mode MOSFET that follows, determine
what operating region the MOSFET is in if the threshold voltage V
T
is 3 V.
a. V
gs
2 V, V
ds
5 V
b . V
gs
4 V, V
ds
5 V
c. V
gs
6 V, V
ds
5 V
d. V
gs
2.5 V
alc80237_ch03_073-116.indd 115alc80237_ch03_073-116.indd 115 1/3/11 3:47 PM1/3/11 3:47 PM
Confirming Pages
116 CHAPTER 3 Semiconductor Electronics
BIBLIOGRAPHY
Bailar, J. et al., Chemistry, Academic Press, New York, 1978.
Gibson, G. and Liu, Y., Microcomputers for Engineers and Scientists, Prentice-Hall,
Englewood Cliffs, NJ, 1980.
Horowitz, P. and Hill, W., The Art of Electronics, 2nd Edition, Cambridge University Press,
New York, 1989.
Johnson, D., Hilburn, J., and Johnson, J., Basic Electric Circuit Analysis, 2nd Edition,
Prentice-Hall, Englewood Cliffs, NJ, 1984.
Lerner, R. and Trigg, G., Encyclopedia of Physics, VCH Publishers, New York, 1991.
McWhorter, G. and Evans, A., Basic Electronics, Master Publishing, Richardson, TX, 1994.
Millman, J. and Grabel, A., Microelectronics, 2nd Edition, McGraw-Hill, New York, 1987.
Mims, F., Engineer’s Mini-Notebook: Basic Semiconductor Circuits, Radio Shack Archer
Catalog No. 276-5013, 1986.
Mims, F., Engineer’s Mini-Notebook: Optoelectronics Circuits, Radio Shack Archer Catalog
No. 276-5012A, 1986.
Mims, F., Getting Started in Electronics, Radio Shack Archer Catalog No. 276-5003A, 1991.
Rizzoni, G., Principles and Applications of Electrical Engineering, 5th Edition, McGraw-
Hill, New York, 2005.
alc80237_ch03_073-116.indd 116alc80237_ch03_073-116.indd 116 1/3/11 3:47 PM1/3/11 3:47 PM
Confirming Pages
117
CHAPTER
4
System Response
T
his chapter describes how to mathematically model a physical system and
characterize its response to dynamic inputs. These topics are important in
understanding how actuators, sensors, amplifiers, filters, and other mecha-
tronic system components function. ■
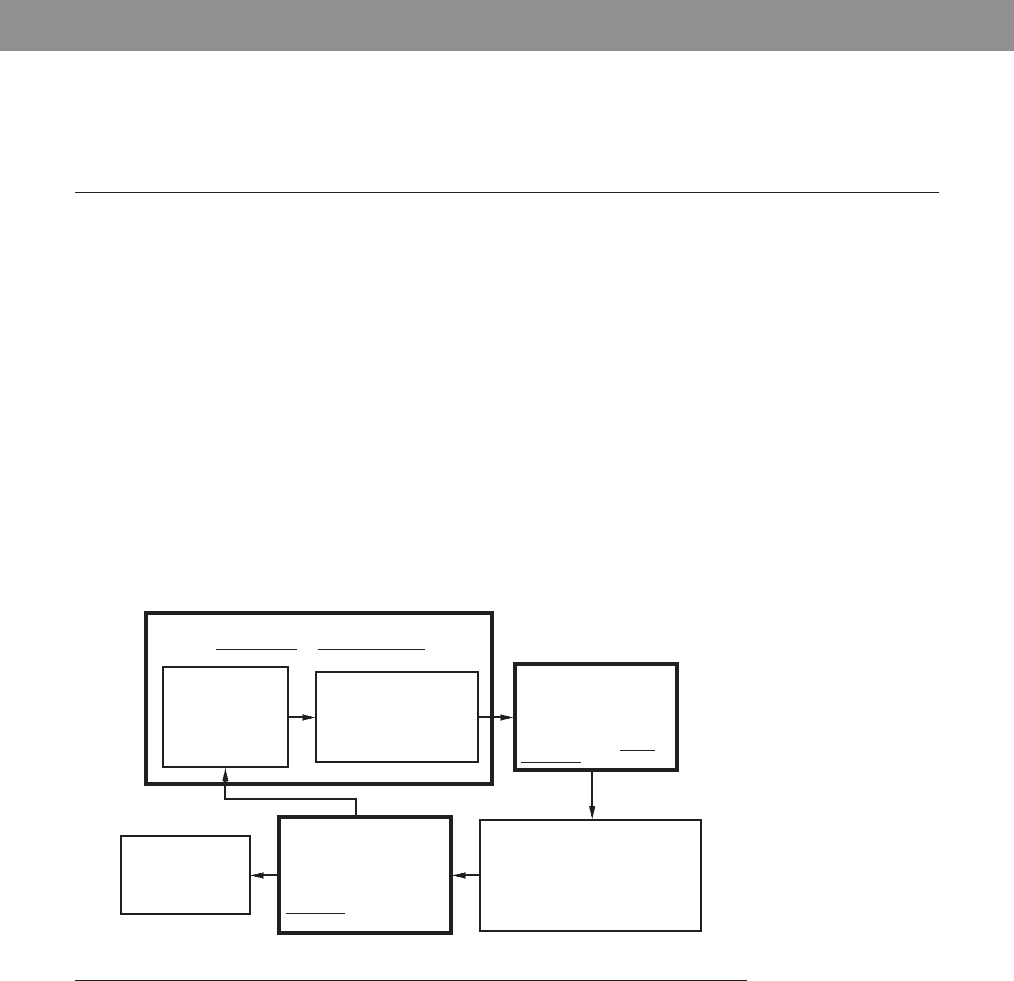
INPUT SIGNAL
CONDITIONING
AND INTERFACING
- discrete circuits
amplifiers
filters
- A/D, D/D
OUTPUT SIGNAL
CONDITIONING
AND INTERFACING
- D/A, D/D
amplifiers
- PWM
- power transistors
- power op amps
GRAPHICAL
DISPLAYS
- LEDs
- digital displays
- LCD
- CRT
SENSORS
- switches
- potentiometer
- photoelectrics
- digital encoder
- strain gage
- thermocouple
- accelerometer
- MEMs
ACTUATORS
- solenoids, voice coils
- DC motors
- stepper motors
- servomotors
- hydraulics, pneumatics
MECHANICAL SYSTEM
system model dynamic response
DIGITAL CONTROL
ARCHITECTURES
- logic circuits
- microcontroller
- SBC
- PLC
- sequencing and timing
- logic and arithmetic
- control algorithms
- communication
CHAPTER OBJECTIVES
After you read, discuss, study, and apply ideas in this chapter, you will:
1. Understand the three characteristics of a good measurement system: amplitude
linearity, phase linearity, and adequate bandwidth
2. Be able to define the Fourier series representation of a signal and use it to show
the components of the spectrum of the signal
3. Understand the relationship between an instrument’s bandwidth and the spectra
of its input and output signals
alc80237_ch04_117-160.indd 117alc80237_ch04_117-160.indd 117 1/4/11 3:48 PM1/4/11 3:48 PM
Confirming Pages
118 CHAPTER 4 System Response
4. Understand the dynamic response of zero-, first-, and second-order measure-
ment and mechatronic systems
5. Be able to use step and sinusoidal inputs to analyze and characterize the
response of measurement and mechatronic systems
6. Understand the analogies among mechanical, electrical, and hydraulic systems.
4.1 SYSTEM RESPONSE
The relationship between the desired output of a mechatronic or measurement sys-
tem and its actual output is the basis of system response analysis. This chapter deals
with analysis techniques that characterize and predict how linear systems respond to
specific inputs. We concentrate on measurement systems, which are often integral
parts of mechatronic systems.
As we saw in Chapter 1, a measurement system consists of three parts: a trans-
ducer, a signal processor, and a recorder. A transducer is a device that usually con-
verts a physical quantity into a time-varying voltage, called an analog signal. A
signal processor can modify the analog signal, and a recorder provides either a tran-
sitory display or storage of the signal. The physical variable we wish to measure is
called the input to the measurement system. The transducer transforms the input into
a form compatible with the signal processor, which in turn modifies the signal, which
then becomes the output of the measurement system. Usually, the recorded output
is different from the actual input, as illustrated in Figure 4.1. Generally, we want to
have the reproduced output signal match the input as closely as possible unless there
is information in the input that we want to eliminate (e.g., electrical noise).
Certain conditions must be satisfied to accomplish adequate reproduction of the
input. For a measurement system with time-varying inputs, three criteria must be
satisfied in order to ensure that we obtain a quality measurement:
1. Amplitude linearity
2. Adequate bandwidth
3. Phase linearity
We examine each of these criteria in detail in the following sections.
4.2 AMPLITUDE LINEARITY
A good measurement system satisfies the criterion of amplitude linearity. Mathemat-
ically, this is expressed as
V
out
t() V
out
0()– α V
in
t() V
in
0()–[]=
(
4.1)
where is a constant of proportionality. This means that the output always changes by
the same factor times the change in the input. If this does not occur, then the system
is not linear with respect to amplitude, and it becomes more difficult to interpret the
alc80237_ch04_117-160.indd 118alc80237_ch04_117-160.indd 118 1/4/11 3:48 PM1/4/11 3:48 PM
Confirming Pages
4.2 Amplitude Linearity 119
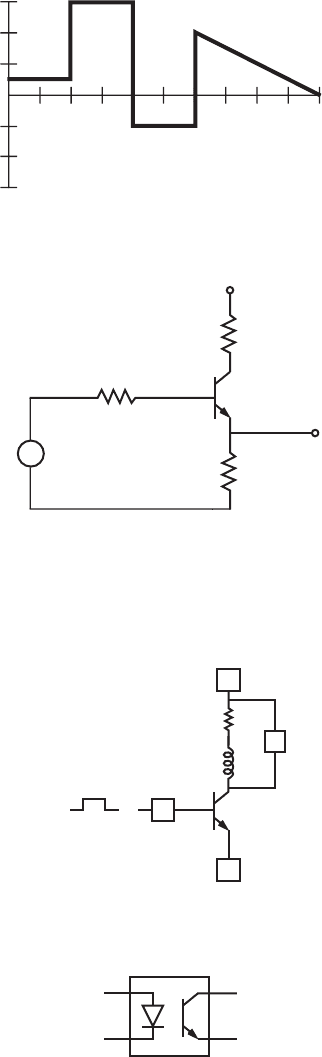
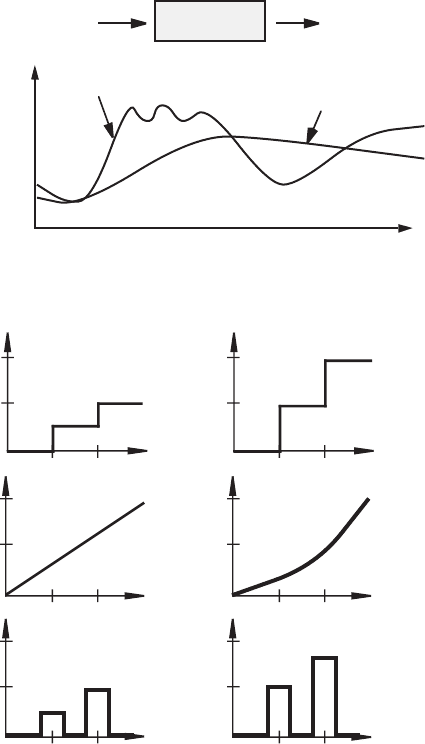
output. Figure 4.2 displays examples of amplitude linearity and nonlinearity. The
first example is linear and 20. The second two examples are nonlinear because
is not constant. In the third example, the output changes by a factor of 20 on the first
pulse and by a factor of 15 on the second pulse.
Normally, a measurement system will satisfy amplitude linearity over only a lim-
ited range of input amplitudes. Also, the system usually responds linearly only when
the rate of change of the input is within certain limits. This second issue is related to
the bandwidth of the system, addressed in Section 4.4. An ideal measurement system
will exhibit amplitude linearity for any amplitude or frequency of the input.
Figure 4.2 A mplitude linearity and nonlinearity.
0
1
2
0
1
2
0
1
2
0
10
20
0
10
20
0
10
20
linear
nonlinear
nonlinear
input output
tt
t
t
t t
Figure 4.1 M e a surement system input-output.
measurement
system
actual
input
recorder
output
actual input
recorded output
analog
voltage
time
alc80237_ch04_117-160.indd 119alc80237_ch04_117-160.indd 119 1/4/11 3:48 PM1/4/11 3:48 PM
Confirming Pages
120 CHAPTER 4 System Response
4.3 FO URIER SERIES REPRESENTATION
OF SIGNALS
Before we look at the concepts of bandwidth and phase linearity, which apply to fre-
quency components of an input signal, we first need to review the concept of Fourier
series representation of a signal. The fundamental premise for the Fourier series rep-
resentation of a signal is that any periodic waveform can be represented as an infinite
series of sine and cosine waveforms of different amplitudes and frequencies. When
this infinite series is summed up, it will reproduce the original periodic waveform
exactly. What this means is that we can take any complicated but periodic wave-
form and decompose it into a series of sine and cosine waveforms. In practice, we
do not need the entire infinite series because a finite number of the sine and cosine
waveforms can adequately represent the original signal.
We define the fundamental or first harmonic
0
as the lowest frequency com-
ponent of a periodic waveform. It is inversely proportional to the period T:
ω
0
2π
T
------ 2πf
0
==
(4.2)
where f
0
is the fundamental frequency expressed in hertz (Hz). The other sine and
cosine waveforms have frequencies that are integer multiples of the fundamental fre-
quency. The second harmonic would be 2
0
, the third harmonic would be 3
0
, and
so on. The Fourier series representation of an arbitrary periodic waveform f(t) can
be expressed mathematically as
F
(4.3)
where the constant C
0
is the DC component of the signal, and the two summations are
infinite series of sine and cosine waveforms. The coefficients of the sine and cosine
terms are defined by
A
n
2
T
---
ft() nω
0
t()dtcos
0
T
∫
=
(4.4)
B
n
2
T
−
ft() nω
0
t()dtsin
0
T
∫
=
(4.5)
where f(t) is the waveform being represented and T is the period of the waveform.
The DC term C
0
represents the average value of the waveform over its period; there-
fore, it can be expressed as
C
0
1
T
−
ft() td
0
T
∫
A
0
2
−−
==
(4.6)
where A
0
is given by substituting n = 0 into Equation 4.4.
alc80237_ch04_117-160.indd 120alc80237_ch04_117-160.indd 120 1/4/11 3:48 PM1/4/11 3:48 PM
