Alciatore D.G., Histand M.B. Introduction to Mechatronics and Measurement Systems

Подождите немного. Документ загружается.

Confirming Pages

4.10 Second-Order System 141

Equations 4.63 and 4.66 define how the terms in this equation relate to the coeffi-

cient parameters in Equation 4.56.

■ CLASS DISCUSSION ITEM 4.5

Spring-Mass-Damper System in Space

Would a spring-mass-damper system behave any differently inside a space station

orbiting the earth than it does on the surface of the earth? Why or why not? How could

you use a spring to measure the mass of an astronaut in the orbiting space station?

4.10.1 Step Response of a Second-Order System

As we found when analyzing a first-order system, an important input used to study

the dynamic characteristics of a system is a step function. The step response is a

good measure of how fast and smoothly a system responds to abrupt changes in

input. The step response consists of two parts: a transient homogeneous solution

(t), which is of the form presented in Section 4.10 for the unforced response, plus

a steady state particular solution x

(t), which is a result of the forcing function. For

a step input given by

ext

t()

0 t 0<

t 0≥

⎩

⎨

⎧

(4.73)

it is clear from Equation 4.56 that a particular solution is

t()

----

(4.74)

The general solution for the step response is then

x(t) = x

(t) + x

(t)

(4.75)

where the constants in x

(t) are determined by applying the initial conditions x(0)

and dx /dt(0) to the general solution x(t). As with the unforced case, there are three

distinctly different types of response based on the amount of damping in the system,

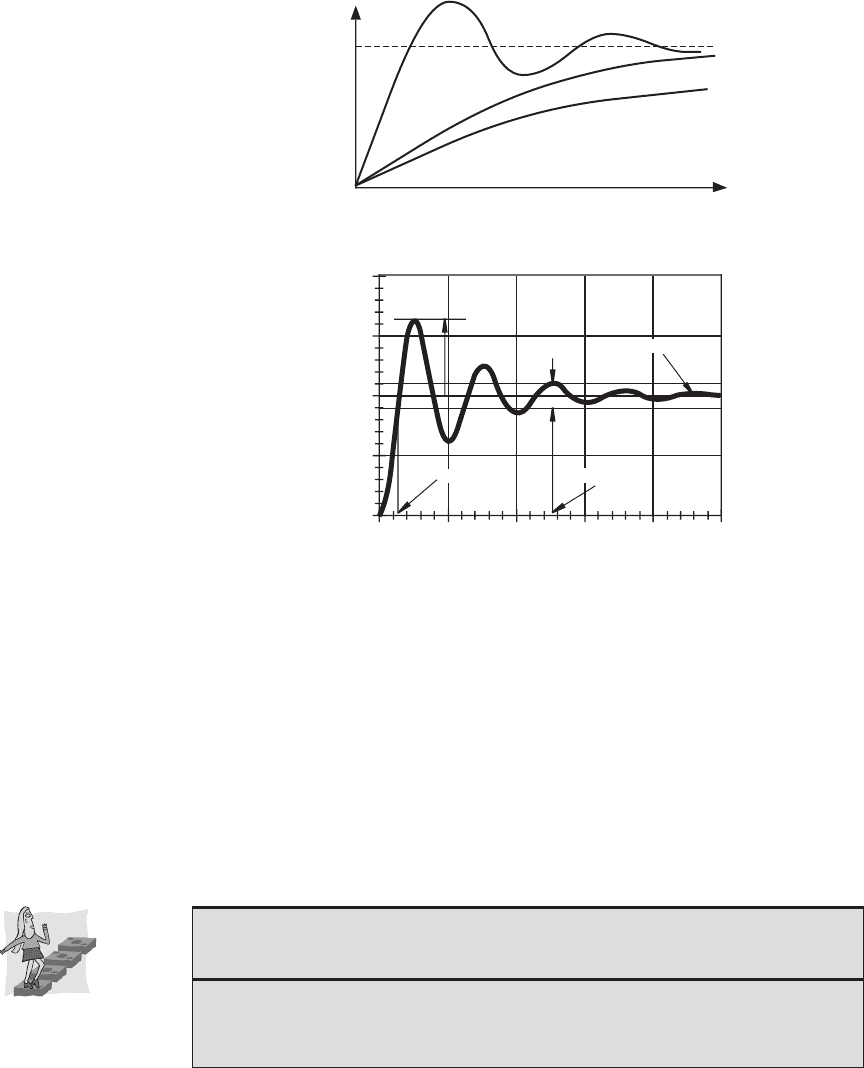
as illustrated in Figure 4.17.

Figure 4.18 illustrates the step response of an underdamped system and defines

several terms used when describing the step response. The steady state value is

the value the system reaches after all transients dissipate. The rise time is the time

required for the system to go from 10% to 90% of the steady state value. The over-

shoot is a measure of the amount the output exceeds the steady state value before

settling, usually specified as a percentage of the steady state value. The settling time

is the time required for the system to settle to within an amplitude band whose width

is a specified percentage of the steady state value. A settling time tolerance band

of 10% is shown in Figure 4.18, although, 2% is more commonly used when

calculating and reporting values. These terms can be used to characterize the step

alc80237_ch04_117-160.indd 141alc80237_ch04_117-160.indd 141 1/4/11 3:48 PM1/4/11 3:48 PM

Confirming Pages

Figure 4.17 Second-order step responses.

underdamped

critically damped

overdamped

x(t)

Figure 4.18 Features of an underdamped step response.

0.5

1.5

12345

step response x(t)

rise time

time

overshoot

settling time

±10%

ζ = 0.15

steady state value

142 CHAPTER 4 System Response

response of a second-order system with different amounts of damping: An under-

damped system exhibits a fast rise time, but it overshoots and may take a while to

settle, although, with the right amount of damping, it can settle faster than critically

damped or overdamped systems. For cases where no overshoot is allowed or desired,

a critically damped system has the fastest rise and settle times. An overdamped sys-

tem also has no overshoot, but has slower rise and settle times.

The step response may be useful in identifying the order of a system, because

the shape of the response curve can help indicate the order. Also, if the system is

second order, we can learn whether it is underdamped, overdamped, or critically

damped.

■ CLASS DISCUSSION ITEM 4.6

Good Measurement System Response

Describe and sketch what you think is a “good” step response of a measurement

system. Is overshoot bad? What advantage does it provide? Does critical damping

provide optimal response?

alc80237_ch04_117-160.indd 142alc80237_ch04_117-160.indd 142 1/4/11 3:48 PM1/4/11 3:48 PM

Confirming Pages

4.10 Second-Order System 143

4.10.2 Frequency Response of a System

To deter mine the frequency response of a linear system, we apply a sinusoidal input

and determine the output response for different input frequencies. For the second-

order system described in Section 4.10, the sinusoidal forcing function input can be

represented as

ext

()

ωt

()

(4.76)

where F

is the amplitude of the external force and ω is the input frequency.

When the sinusoidal input is first applied, the system exhibits a combined tran-

sient and steady state response. Once the transients dissipate, the steady state output

of the system is sinusoidal with the same frequency as the input but possibly out

of phase with the input. We can represent this steady state output in the following

general form:

()

ωt

()

sin=

(4.77)

where X

is the output magnitude and φ is the phase difference between the input and

the output.

The procedure to determine analytically the frequency response of a linear sys-

tem follows. The linear system could model a measurement system or a more gen-

eral mechatronic system of any order. Each step in the procedure is shown in its

generic form and then applied to a second-order system.

Analytical Procedure to Determine the Frequency Response of a System

1. Find the Laplace transform of the system differential equation assuming initial

conditions are zero: x(0) = dx/dt (0)  0. The Laplace transform converts the

differential equation into an algebraic equation that is related to the frequency

response of the system.

The governing equation for a second-order system (from Equation 4.72) can

be expressed as

x(t)

_____

 2

dx(t)

____

 

x(t) 



___

ext

(t)

(4.78)

Applying the Laplace transform to both sides of the equation, assuming zero

initial conditions, gives

 2

s  

)X(s) 



___

ext

(S)

(4.79)

where F

ext

(s) and X(s) are the Laplace transforms of the input forcing function

and the output displacement, respectively.

2. Find the transfer function of the system, which is the ratio of the output and

input Laplace transforms.

For this system, the transfer function is

G(s) 

X(s)

_____

ext

(s)





___

____________

 2

s  

)

(4.80)

alc80237_ch04_117-160.indd 143alc80237_ch04_117-160.indd 143 1/4/11 3:48 PM1/4/11 3:48 PM

Confirming Pages

144 CHAPTER 4 System Response

3. To simulate a harmonic input, replace s with jω in the transfer function. This

yields the frequency response behavior of the system.

For this system, replacing s with j in Equation 4.80 and dividing the numera-

tor and denominator by 

gives

G jω()

1 k⁄

−−−

–j2ζ

−−−

−−−−−−−−−−−−−−−−−−−−−−−−−

( ) ( )

(4.81)

4. Find the desired amplitude ratio between the output and input by determining

the magnitude of the complex transfer function:

mag G jω()[]G jω()=

(4.82)

For this system, taking the magnitude of the denominator, which is the square

root of the sum of the squares of the real and imaginary components, and

moving the k term to the left side of the equation, results in the following

dimensionless ratio:

k⁄

−

−−−

–

4ζ

−−−

⁄

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

( ) ( )

{ }

(4.83)

5. Find the phase angle φ between the output and input by determining the

argument of the complex transfer function:

G jω

()

[]arg G jω

()

∠==

(4.84)

From Equation 4.81, recalling that the argument of a complex number is the

arctangent of the ratio of its imaginary and real parts and that the argument of a

ratio is the difference of the numerator and denominator arguments, the phase

angle for this system is found as

φ 0tan

1–

2ζ

−−−

–

−−−−−−−−−−−−−−

– tan

1–

2ζ

−−−

–

−−−−−−−−

–

( )

(4.85)

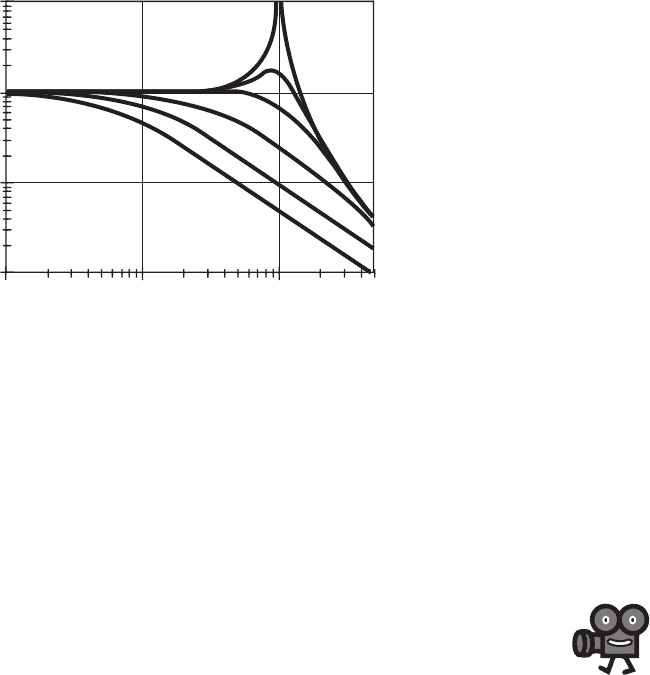
A plot of the frequency response of the second-order system as a function of the

damping ratio  is shown in Figure 4.19. MathCAD Example 4.5 includes the analy-

sis used to create the plot. When the input frequency ω equals the natural frequency

(i.e., /

 1), resonance occurs. Often 

is called the resonant frequency.

For small damping ratios, the output amplitude becomes quite large at the resonant

frequency. For input frequencies less than the natural frequency (i.e., /

 1), the

amplitude ratio is close to 1. The damping ratio ζ affects the range of frequencies

MathCAD Example

4.5Second-order

system frequency

response

alc80237_ch04_117-160.indd 144alc80237_ch04_117-160.indd 144 1/4/11 3:48 PM1/4/11 3:48 PM

Confirming Pages

Figure 4.19 Second-order system amplitude response.

0.01

0.1

amplitude ratio (X

/ F

/k)

0.01

0.1 1

ζ = 0.01

frequency ratio (ω/ω

)

0.707

0.3

4.10 Second-Order System 145

for which this is true. Recall that, for a good measurement system, we require the

amplitude ratio to be nearly constant (within ±3 dB) over the range of frequencies

we wish to measure. A damping ratio of 0.707 provides the best amplitude linearity

over the largest bandwidth.

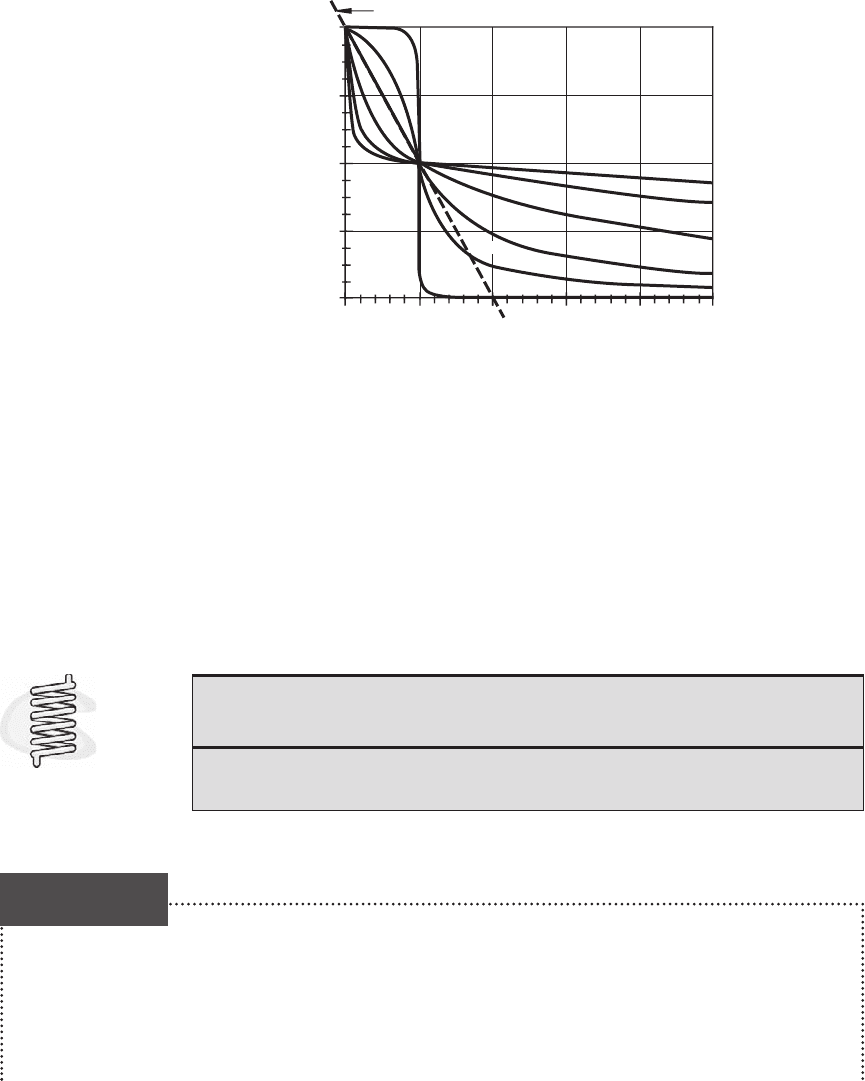
A plot of the phase angle as a function of frequency ratio and damping ratio

is shown in Figure 4.20. The phase angle is negative, implying that the output lags

behind the input, and the magnitude ranges from 0, which represents no phase dif-

ference, to 180, which represents a half-cycle phase difference. As  approaches the

natural frequency 

(i.e., /

 1), the output lags the input by 90 (a quarter of

a cycle). When the damping in a system is very small (e.g.,   0.01) and the value

of the excitation frequency passes through the natural frequency (

), the phase shift

changes abruptly by 180. A damping ratio of 0.707 provides the best approximation

of phase linearity for a second-order system.

A very large number of mechanical systems can be approximated by second-order

linear ordinary differential equations. Also, complex systems or their component sub-

systems can often be reduced to second-order systems for a first approximation analy-

sis. Therefore, all engineers should completely understand all implications of Figures

4.19 and 4.20. Video Demos 4.10 through 4.12 show examples of how the second-

order system response concepts apply to some basic systems. Video Demo 4.13 shows

a classic failure that resulted from engineers not having a firm understanding of some

of these concepts. In this case, there were poorly understood wind-induced oscillating

loads and inadequate damping, leading to catastrophic failure of this famous suspen-

sion bridge.

The output of second-order measurement systems always differs from the

input in both amplitude and phase. In designing a measurement system, the goal

is to minimize these effects when possible, so the choice of 0.707 for the damping

ratio is optimal because it results in the best combination of amplitude linearity

Video Demo

4.10Spring-mass

second-order

system frequency

response

4.11Pendulum

second-order

system frequency

response

4.12Torsional

system frequency

response and

control

4.13Tacoma

Narrows bridge

failure

alc80237_ch04_117-160.indd 145alc80237_ch04_117-160.indd 145 1/4/11 3:48 PM1/4/11 3:48 PM

Confirming Pages

Figure 4.20 Second-order system phase response.

–180

–135

–90

–45

phase angle (°)

ζ = 0.01

0.3

frequency ratio (ω/ω

)

0.707

phase linearity

146 CHAPTER 4 System Response

and phase linearity over the widest range of frequencies. When designing other

types of systems (e.g., see Design Example 4.1, which addresses the design of a

car suspension), damping ratios other than 0.707 might be more appropriate for the

application.

In general, whenever a periodic input is applied to a second-order system, reso-

nance, attenuation, and phase shift may occur. In order to predict how a system will

respond, it is important to be able to determine the system’s frequency response

characteristics.

■ CLASS DISCUSSION ITEM 4.7

Slinky Frequency Response

Using a Slinky with a mass suspended from one end, demonstrate the frequency

response characteristics illustrated in Figures 4.19 and 4.20.

A design team has been asked to select a spring and shock absorber for the front suspension

of a new automobile. The team’s task is to choose a suspension that will provide the best

response to varying road conditions. Since many US manufacturers still specify their prod-

ucts in English units, the design team has reluctantly agreed to perform all analyses using

the English system.

After preliminary analyses and meetings with other design teams, the suspension

team has narrowed its choices down to three alternative suspension designs. The three

Automobile Suspension Selection

DESIGN

EXAMPLE 4.1

alc80237_ch04_117-160.indd 146alc80237_ch04_117-160.indd 146 1/4/11 3:48 PM1/4/11 3:48 PM

Confirming Pages

4.10 Second-Order System 147

alternatives are characterized by the following spring constants k and damping con-

stants b:

Alternative

k (lbf

/in) b (lbf sec /in)

1 500 10

2 200 20

3 120 10

To evaluate the alternatives under different road conditions, the design team decides to

simulate bumps or pot holes as a ground force step input of magnitude F

and regular bumps

or waviness in the road as a sinusoidal ground force input of magnitude B

and frequency ω.

To subject each alternative to similar input displacement levels, the following fixed ratios are

used in the comparison:

⁄ k = 6 in B

⁄ k = 3 in

Each alternative is subjected to the following three frequencies to simulate different speeds

or bump spacing:

= 10 rad/sec ω

= 20 rad/sec ω

= 30 rad/sec

The team decides on a single degree of freedom system that models only a single wheel

and neglects the response of the other wheels. The resulting model is a second-order system

described by Equation 4.56, where m is the mass supported (“sprung”) by the suspension

and F

ext

is the ground force. The weight of the entire vehicle is 2000 lbf; therefore, the

sprung mass supported by a single wheel is assumed to be 1/4 of the total mass:

m = 500 lbm = 15.53 slu

Note that the wheel mass and tire dynamics are not included in this simplified model (see

Class Discussion Item 4.8).

Using Equations 4.63 and 4.66, the natural frequency 

and the damping constant 

are calculated for each alternative:

Alternative 



1 19.6 0.20

2 12.4 0.62

3 9.6 0.40

Since   1.0 for each alternative, the suspensions will exhibit an underdamped step

response described by Equation 4.69.

The step response and sinusoidal response analyses are performed in MathCAD (see

MathCAD Example 4.6). The input variables (for Alternative 1) are defined as

k := 500

lbf

------

b := 10 lbf

sec

-------

m := 500 lb

:= 6in()kB

:= 3in()k

:= 10

rad

sec

-------

:= 20

rad

sec

-------

:= 30

rad

sec

-------

:= 0 sec, 0.01 sec . . 2 sec

MathCAD Example

4.6Suspension

design

(continued )

alc80237_ch04_117-160.indd 147alc80237_ch04_117-160.indd 147 20/01/11 5:45 PM20/01/11 5:45 PM

Confirming Pages

148 CHAPTER 4 System Response

The step response is defined by (see Question 4.28)

---- ζ :=

2 km

--------------

:= ω

1 ζ

–

xt()

----- -

ζ– ω

– ω

t()cos

and the sinusoidal response is defined by

ω() :=

----- -

------

⎝⎠

⎛⎞

–

4ζ

------

⎝⎠

⎛⎞

-----------------------------------------------------------------

φω() := angle–

------

–

⎝⎠

⎛⎞

, 2ζ

xtω,()

:= X

ω() ωt φω()+()sin[]

The results for the three alternatives follow.

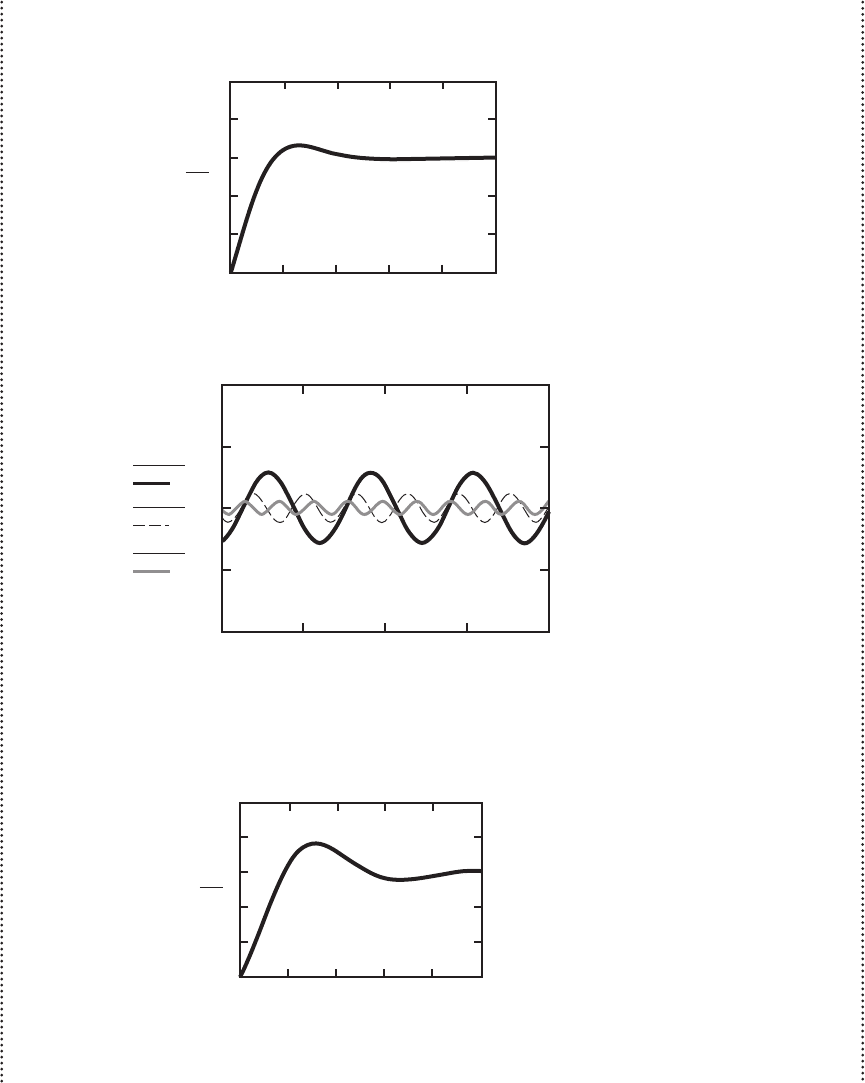
■ Alternative 1

Step Response

0 0.2 0.4 0.6 0.8 1

x(t)

t (sec)

Sinusoidal Response

x (t, ω

)

x (t, ω

)

x (t, ω

)

0 0.5 1 1.5 2

–10

–5

t (sec)

(continued )

alc80237_ch04_117-160.indd 148alc80237_ch04_117-160.indd 148 1/4/11 3:48 PM1/4/11 3:48 PM

Confirming Pages

4.10 Second-Order System 149

■ Alternative 2

Step Response

0.2

0.4

0.6 0.8 1

x (t)

t (sec)

Sinusoidal Response

x (t, ω

) 5

x (t, ω

)

x (t, ω

)

0 0.5 1 1.5 2

–10

–5

t (sec)

■ Alternative 3

x (t)

0 0.2 0.4 0.6 0.8

t (sec)

Step Response

(continued )

alc80237_ch04_117-160.indd 149alc80237_ch04_117-160.indd 149 1/4/11 3:48 PM1/4/11 3:48 PM

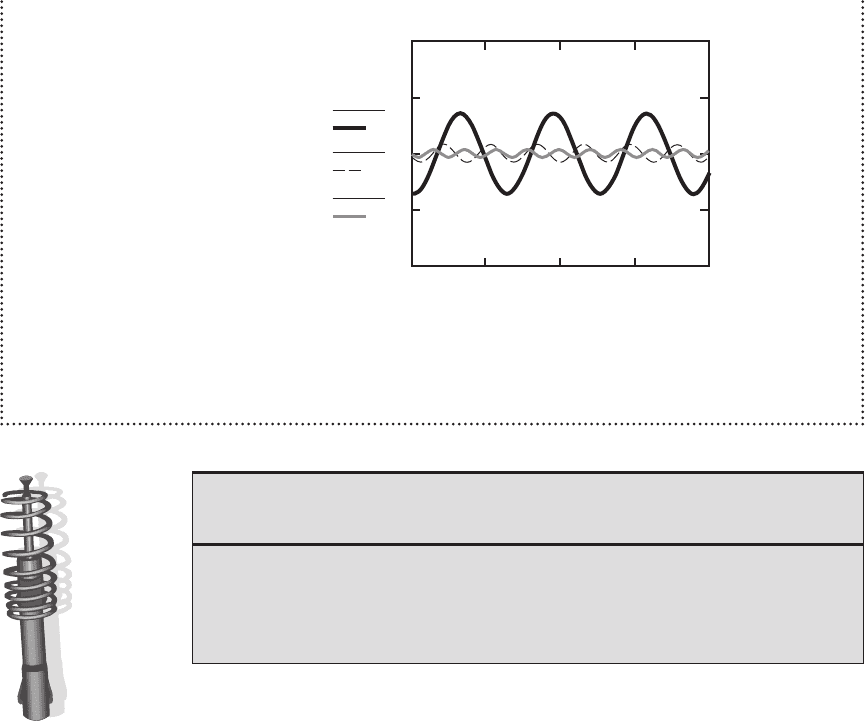
Confirming Pages

150 CHAPTER 4 System Response

x(t, ω

)

x(t, ω

)

x(t, ω

)

Sinusoidal Response

0 0.5 1 1.5 2

–10

–5

t (sec)

A good suspension has a fast response (short settling time), resulting in good handling,

and prevents excessive bounce (oscillation) or large displacement, which improves rider com-

fort. From the preceding results, it appears that Alternative 2 is the best of the three designs. The

step response settles fast with little bounce and the sinusoidal responses have low amplitude.

(concluded )

■ CLASS DISCUSSION ITEM 4.8

Suspension Design Results

Were the step response and sinusoidal response graphs required to draw conclusions

about the three alternatives? Also, why was the amplitude of the sinusoidal response

excessive for Alternative 1 and least for Alternative 2? What would it take to include

the wheel mass and tire dynamics in the system model?

4.11 SYSTEM MODELING AND ANALOGIES

Any system—whether i t be mechanical, electrical, hydraulic, thermal, or some

combination—can be modeled by ordinary linear differential equations that relate the

output responses of the system to the inputs. These differential equations are all very

similar mathematically and differ only in the constants that appear in front of the deriva-

tive terms. These constants represent the physical parameters of the system, and there

are analogies for these parameters among the different system genres. For instance, a

resistor in an electrical system is analogous to a dashpot or damper in a mechanical sys-

tem or to a valve or flow restriction in a hydraulic system. Similarly, mass or inertia in a

mechanical system is analogous to inductance in an electrical system and fluid inertance

in a hydraulic system. The generic terms used to describe the analogous system parame-

ters and variables are effort, flow, displacement, momentum, resistance, capacitance,

and inertia. Table 4.1 summarizes the generic quantities along with specific analogies

for mechanical, electrical, and hydraulic systems. Also included are equations relating

variables for energy storage and energy dissipation elements in each system.

alc80237_ch04_117-160.indd 150alc80237_ch04_117-160.indd 150 1/4/11 3:48 PM1/4/11 3:48 PM