Alciatore D.G., Histand M.B. Introduction to Mechatronics and Measurement Systems

Подождите немного. Документ загружается.

Confirming Pages

Figure 4.10 Phase distortion o f a square wave (generated with MathCAD).

t := 0, 0.01 . . 2 n := 1 . . 50

π 2n 1–()

-----------------------

:= 0.05 1 exp 2n 1–()–[]–{}

lag

t() := B

2n 1–()2π tdt

–()[]sin

∑

lead

t() := B

2n 1–()2π tdt

+()[]sin

∑

0 1 2

lag

(t)

0 1 2

lead

(t)

(a) high-frequency components lagging (b) high-frequency components leading

4.7 Dynamic Characteristics of Systems 131

4.7 DYNAMIC CHARACTERISTICS

OF SYSTEMS

As we will see, many measurement systems can be modeled as linear ordinary dif-

ferential equations with constant coefficients. This is also true of many mechatronic

systems or their component subsystems. These linear models have the following

general form:

n = 0

∑

out

---------------

m = 0

∑

--------------

(4.30)

where X

out

is t he output variable, X

is the input variable, and A

and B

are constant

coefficients. N defines the order of the system independent of M. The approach used

to determine the differential equation model depends on the type of system being

analyzed. For example, Newton’s laws and free-body diagrams can be applied to

mechanical systems, and KVL and KCL equations can be applied to electric circuits.

■ CLASS DISCUSSION ITEM 4.3

Analytical Attenuation

In Figure 4.9, the following exponential terms were used to attenuate amplitude

components at either low or high frequencies:

−0.1(2n − 1)

and 1e

−(2n − 1)

Explain how these exponential terms cause the resulting distortion of the square wave.

(Hint: Plot the exponential functions and describe how they change the amplitudes of

the components of the square wave spectrum.)

alc80237_ch04_117-160.indd 131alc80237_ch04_117-160.indd 131 1/4/11 3:48 PM1/4/11 3:48 PM

Confirming Pages

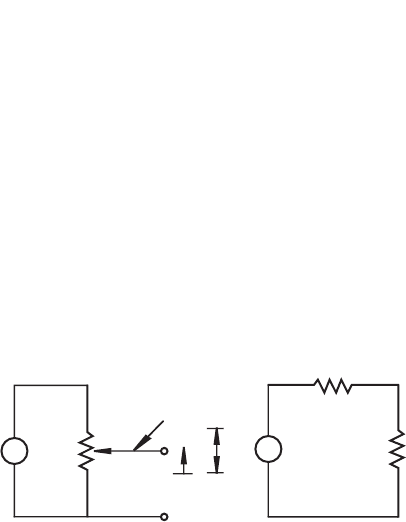
Figure 4.11 Displacement potentio meter.

wiper

out

L – x

= R

– R

= (X

/L)R

–

potentiometer

equivalent circuit

–

L – x

132 CHAPTER 4 System Response

As we will see, the constant coefficients A

represent physical properties of the sys-

tem of interest.

Many electromechanical systems exhibit nonlinear behavior and cannot be accu-

rately modeled as linear systems. However, a nonlinear system may often exhibit

linear behavior over a limited range of inputs and a linear model can be derived that

provides an adequate approximation over this range. This process of modeling a

nonlinear system with a linear model is called linearization.

The next three sections present methods to characterize the simplest and most

common forms of Equation 4.30, where M = 0 and N = 0, 1, or 2. These cases are

referred to as zero-order, first-order, and second-order systems, respectively.

4.8 ZERO-ORDER SYSTEM

W hen N = M = 0 in Equation 4.30, the model represents a zero-order system whose

behavior is described by

out

(4.31)

out

-----

(4.32)

where K = B

is a constant referred to as the gain or sensitivity of the system,

because it represents a scaling between the input and the output. When the sensitivity

is high, a small change in the input can result in a significant change in the output.

Note that the output of a zero-order system follows the input exactly with no time

delay or distortion.

An example of a zero-order measurement system is a potentiometer used to

measure displacement. A potentiometer is a variable resistance device whose output

resistance changes as an internal wiper moves across a resistive surface. As illus-

trated in Figure 4.11, it produces an output voltage V

out

that is directly proportional to

the wiper displacement X

. This is a result of the voltage division rule, which gives

out

-----

⎝⎠

⎛⎞

(4.33)

alc80237_ch04_117-160.indd 132alc80237_ch04_117-160.indd 132 1/4/11 3:48 PM1/4/11 3:48 PM

Confirming Pages

4.8 Zero-Order System 133

where R

is the re sistance between the potentiometer leads, R

is the maximum resis-

tance of the potentiometer, X

is the displacement of the potentiometer wiper, and L

is the maximum amount of wiper travel.

■ CLASS DISCUSSION ITEM 4.4

Assumptions for a Zero-Order Potentiometer

What approximating assumptions must be made regarding the potentiometer to

ensure that it is a zero-order measurement system?

THREADED DESIGN EXAMPLE

DC motor power-op-amp speed controller—potentiometer interface A.2

The figure below shows the functional diagram for Threaded Design Example A (see Section

1.3 and Video Demo 1.6). The portion described here is highlighted.

potentiometer

PIC microcontroller

with analog-to-digital

converter

power

amp

motor

A/D D/A

light-

emitting

diode

digital-to-analog

converter

To interface a potentiometer to a microcontroller, the analog voltage output (see Equation

4.30) must be converted to digital form. Fortunately, a PIC microcontroller can be selected that has

a built-in analog-to-digital (A/D) converter. This allows the PIC to sense the potentiometer posi-

tion, as a voltage, using the simple circuit shown below. The potentiometer has three leads, wired

as shown, with the center “wiper” lead connected to the PIC analog input (pin 18, designated as

AN1). The voltage on the wiper line varies from 0 V (ground) to 5 V as the knob is turned.

PIC16F88

microcontroller

AN1

5 V

wiper

5 V

wiper

ground

potentiometer

schematic symbol

actual

potentiometer

layout

knob

10 kΩ

pot

Video Demo

1.6DC motor

power-op-amp

speed controller

alc80237_ch04_117-160.indd 133alc80237_ch04_117-160.indd 133 1/4/11 3:48 PM1/4/11 3:48 PM

Confirming Pages

134 CHAPTER 4 System Response

4.9 FIRST-ORDER SYSTEM

Whe n N = 1 and M = 0 in Equation 4.30, the equation models a first-order system

whose behavior is described by

out

------------

out

+ B

(4.34)

-----

out

------------

out

-----

(4.35)

As with the zero-order system, the coefficient ratio on the right-hand side is called

the sensitivity or static sensitivity, defined as

-----

(4.36)

The coefficient ratio on the left side of Equation 4.35 has a special name and meaning.

It is called the time constant and is defined as

-----

(4.37)

Why we chose this name will become clear in the subsequent analysis. With these

definitions, the first-order system equation can be written as

out

------------

out

+ KX

(4.38)

Note that in this standard form, the coefficent of the X

out

term must be 1.

To characterize how a sys tem responds to various types of inputs, we apply

standard inputs to the model, including step, impulse, and sinusoidal functions. A

step input changes instantaneously from 0 to a constant value A

and is stated math-

ematically as

0 t 0<

t 0≥

⎩

⎨

⎧

(4.39)

The output of the system i n response to this input is called the step response of the

system. For a first-order system, we can find the step response by solving Equation

4.38 using Equation 4.39 with the initial condition

out

(0)

(4.40)

Assuming a solut ion of the form Ce

for the homogeneous form of differential

Equation 4.38, the characteristic equation is

τs + 1 = 0

(4.41)

alc80237_ch04_117-160.indd 134alc80237_ch04_117-160.indd 134 1/4/11 3:48 PM1/4/11 3:48 PM

Confirming Pages

4.9 First-Order System 135

Since the root of this equation is s = −1/τ, the homogeneous or transient solution is

out

C e

t τ⁄–

(4.42)

where C is a constant determ ined later by applying initial conditions. A particular

or steady state solution resulting from the step input is

out

(4.43)

The general solution is the sum of the homogeneous and particular solutions

(Equation 4.42 + Equation 4.43):

out

t() X

out

+ C e

t τ⁄–

+==

(4.44)

Applying the initial condition ( Equation 4.40) to this equation gives

0 CKA

(4.45)

thus,

CKA

–=

(4.46)

so the resulting step response is

out

t() KA

t τ⁄–

–(

)

(4.47)

As illustrated in Figure 4.12, this represents an exponential rise in the output toward

an asymptotic value of KA

. The rate of the rise depends only on the time constant τ.

The response is faster for a smaller time constant.

Note that after one time constant, the output reaches 63.2% of its final value,

and from Equation 4.46,

out

τ() KA

–

–()0.632KA

(4.48)

After four time constants, the s tep response is

out

4τ() KA

–

–()0.982KA

(4.49)

Since this value is more than 98% of the steady state value KA

, we usually ass-

ume that a first-order system has reached its steady state value within four time

constants.

Figure 4.12 First-order response.

small τ

large τ

alc80237_ch04_117-160.indd 135alc80237_ch04_117-160.indd 135 1/4/11 3:48 PM1/4/11 3:48 PM

Confirming Pages

136 CHAPTER 4 System Response

When designing a first-order measurement system, look at quantities that affect

τ and try to reduce them if possible. The larger τ is, the longer the measurement sys-

tem takes to respond to an input.

An important example of a first-order system is an RC circuit (see Example 4.1),

which has a time constant of τ = RC (see Question 4.19). RC circuits are very com-

mon in timing, filter, and other applications (e.g., see Example 4.1, Section 6.12.3,

and Example 7.6). Video Demo 4.9 illustrates the step response of an RC circuit,

showing how the voltage across the capacitor builds over time. The speed of charg-

ing and discharging the capacitor is directly related to the time constant of the circuit.

4.9.1 Experimental Testing of a First-Order System

To characterize and evaluate an existing first-order system, we need methods to

experimentally determine the time constant τ and the static sensitivity K. K may be

obtained by static calibration, where a known static input is applied, and the output

is observed. A common method to determine the time constant τ is to apply a step

input to the system and determine the time for the output to reach 63.2% of its final

value (see Equation 4.48). An alternative method to determine a value for τ follows.

We can rearrange Equation 4.47, expressing it as

out

–

---------------------------

t τ⁄–

–=

(4.50)

Simplifying, we get

out

------------–e

t τ⁄–

(4.51)

If we take the natural logarithm of both sides, we get

out

------------–

⎝⎠

⎛⎞

–=

(4.52)

If we define the left-hand side as Z, then

Ztτ

⁄

–=

(4.53)

and a plot of Z vs. t is a straight line with the slope

------

-- -

–=

(4.54)

Therefore, if we collect experimental data from a step response and plot Z vs. t as

illustrated in Figure 4.13, we can determine τ from the slope of the line:

ΔZ

-------

–=

(4.55)

Note that if experimental data fo r Z vs. t deviates from a straight line, then the

system is not first order. If this is the case, the system is either of higher order or

nonlinear.

Video Demo

4.9RC circuit

charging and

discharging

alc80237_ch04_117-160.indd 136alc80237_ch04_117-160.indd 136 1/4/11 3:48 PM1/4/11 3:48 PM

Confirming Pages

Figure 4.13 Experimental determination of τ.

–Z

experimental data for X

out

–ΔZ

Δt

Figure 4.14 Second-order mechanical system and free -body diagram.

free-body diagram

of mass

b dx/d

ext

4.10 Second-Order System 137

4.10 SECOND-ORDER SYSTEM

An example of a second-order system, where N = 2 in Equation 4.30, is the mechan-

ical spring-mass-damper system illustrated in Figure 4.14. Applying Newton’s law

of motion (in this case, ΣF

= ma

) to the free-body diagram gives the second-order

differential equation, which is the mathematical model for the system:

--------

----- -

kx++ F

ext

t()=

(4.56)

where m is the mass, b is the damping coefficient, k is the spring constant, and x

is the displacement of the mass from the equilibrium (rest) position of the mass

measured positively in the downward direction as shown. F

ext

(t) represents the resul-

tant of all applied external forces (inputs) in the direction of x. The weight of the

mass is not included as a force in the free-body diagram because the displacement

x is measured from the equilibrium position. In the equilibrium position, the spring

is stretched an amount  from its unstretched length so that the effect of gravity

alc80237_ch04_117-160.indd 137alc80237_ch04_117-160.indd 137 1/4/11 3:48 PM1/4/11 3:48 PM

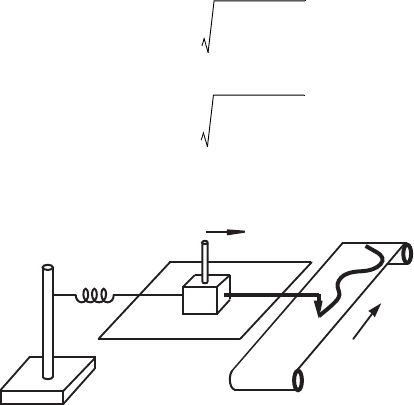
Confirming Pages

Figure 4.15 Strip chart recorder as an example of a second-order system.

fixed rigid support

elastic spring (k)

mass (m)

bearing support (b)

pen-paper contact

applied force (F

ext

)

138 CHAPTER 4 System Response

is balanced: k  mg. Note that the spring force (kx) is in the opposite direction from

the mass displacement, and the damper force (b dx/dt) is in the opposite direction

from the velocity of the mass.

As we will see in Section 4.11, the governing equations for many second-order

systems other than mechanical spring-mass-damper systems (e.g., mechanical rota-

tional systems and hydraulic systems) have the same form as Equation 4.56.

A good example of a second-order measurement system is the strip chart

recorder illustrated in Figure 4.15. It consists of a continuously moving roll of paper

on which a pen is moved back and forth. A spring is attached to the pen carriage to

keep it centered in a neutral position when an applied force is removed. The strip

chart recorder can be thought of as a mechanical oscilloscope. It was used much

more before the digital age whenever a large amount of time-varying data needed to

be stored (e.g., for later analysis). They are still used in some applications (e.g., in

older remote seismograph stations and polygraph machines). The applied force F

ext

is provided by an electromagnetic coil whose core is attached to the pen carriage.

The spring keeps the pen carriage centered in the zero position when the input is 0.

The pen carriage bearings and the pen-paper interface result in the damping force.

The carriage and the pen constitute the mass to which the forces in the system are

applied.

To characterize the unforced response of a second-order system, we need to

solve the differential Equation 4.56 with F

ext

 0. The characteristic equation is

bs k++ 0=

(4.57)

This quadratic equation has two roots for s:

-------–

---------

⎝⎠

⎛⎞

----–+=

(4.58)

-------–

---------

⎝⎠

⎛⎞

----––=

(4.59)

alc80237_ch04_117-160.indd 138alc80237_ch04_117-160.indd 138 1/4/11 3:48 PM1/4/11 3:48 PM

Confirming Pages

4.10 Second-Order System 139

If there were no damping in the system (i.e., b  0), the roots would be

----=

(4.60)

j–

----=

(4.61)

and the corresponding homogeneous solution would be

t() A

---- t

⎝⎠

⎛⎞

cos B

---- t

⎝⎠

⎛⎞

sin+=

(4.62)

where A and B are constants determine d from the initial conditions x(0) and

dx/dt(0). This motion represents pure undamped oscillatory motion with radian

frequency:

----=

(4.63)

This is called the natural frequency of the system, because it is the frequency at

which the undamped system would naturally oscillate if the spring were stretched

and the mass released and allowed to move without any external force (F

ext

= 0).

If there is damping in the system (i.e., b ≠ 0) and the radicand in Equations 4.58

and 4.59 is zero, the roots are double real roots, and the resulting transient homoge-

neous solution is

t() ABt+()e

t–

(4.64)

This represents an exponentially decaying motion. A system with this behavior is

said to be critically damped, because it is just on the verge of damped oscillatory

motion. The damping constant that results in critical damping is called the critical

damping constant b

. It is the value of b that makes the radicand 0, so

2 km 2mω

(4.65)

The damping ratio ζ (zeta) for a noncr itically damped system is defined as

----

2 km

--------------

(4.66)

It is a measure of the proximity to crit ical damping. A critically damped system has

a damping ratio of 1.

With the definitions of natural frequency and damping ratio, the roots of the

characteristic equations (Equations 4.58 and 4.59) can be written as

ζ– ω

1–+=

(4.67)

ζ– ω

1––=

(4.68)

alc80237_ch04_117-160.indd 139alc80237_ch04_117-160.indd 139 1/4/11 3:48 PM1/4/11 3:48 PM

Confirming Pages

Figure 4.16 Transient response of second-order systems.

–0.5

0.5

transient homogeneous solution

(t)

0.5

1 1.5 2 2.5

time

overdamped

(ζ = 1.75)

critically damped

(ζ = 1.0)

underdamped

(ζ = 0.25)

140 CHAPTER 4 System Response

If there is damping in the system (i.e., b ≠ 0) and the radicand in Equations 4.67

and 4.68 is negative (i.e., ζ < 1), the roots are complex conjugates, and the resulting

transient homogeneous solution is

t() e

ζω

t–

A ω

1 ζ

– t()cos B ω

1 ζ

– t()sin+[]=

(4.69)

This motion represents damped oscillation c onsisting of sinusoidal motion with

exponentially decaying amplitude. A system with these characteristics is said to be

underdamped, because it has less than critical damping (ζ < 1). The frequency of

oscillation is

1 ζ

–=

(4.70)

which is called the damped natural frequency of the system.

If there is damping in the system (i.e., b ≠ 0) and the radicand in Equations 4.67

and 4.68 is positive (i.e., ζ > 1), the roots are distinct real roots and the resulting

transient homogeneous solution is

t() A e

ζ– ζ

1–+()ω

B e

ζ– ζ

1––()ω

(4.71)

This represents an exponentially decaying output. A system with these characteris-

tics is said to be overdamped, because its damping exceeds critical damping (ζ > 1).

Examples of transient responses for all three cases of damping (under-

damped, critically damped, and overdamped) are illustrated in Figure 4.16.

The curves represent unforced motion of a second-order system with different

amounts of damping, when the system is released from rest (dx/dt(0)  0) at

x(0)  1.

Based on the definitions above, a more standard form for the differential equa-

tion representing a second-order system can be written as

x  2

x  

x 



___

ext

(4.72)

alc80237_ch04_117-160.indd 140alc80237_ch04_117-160.indd 140 1/4/11 3:48 PM1/4/11 3:48 PM