Зубов В.Г., Шальнов В.П. Сборник задач по физике
Подождите немного. Документ загружается.

#
èçìåíÿåò åå çíà÷åíèÿ. Ïîýòîìó ñèëà òðåíèÿ áóäåò òà æå,
÷òî è â ïåðâîì ñëó÷àå.
78. Íà òà÷êó äåéñòâóþò ñëåäóþùèå ñèëû: ñèëà òÿæå-
ñòè m
g
H
, ñèëà ðåàêöèè îïîðû (äîðîãè)
R
H
, ñèëà òðåíèÿ
f
H
è ñèëà
F
KH
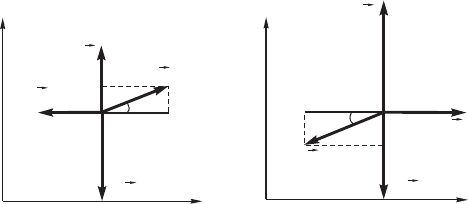
, ïðèêëàäûâàåìàÿ ÷åëîâåêîì. Íà ðèñ. 199, à
èçîáðàæåíû ýòè ñèëû äëÿ ñëó÷àÿ, êîãäà ÷åëîâåê òÿíåò
òà÷êó, à íà ðèñ. 199, á äëÿ ñëó÷àÿ, êîãäà îí åå òîëêàåò
(òî÷êè ïðèëîæåíèÿ ñèë ñîâïàäàþò ñ öåíòðîì ìàññ C òà÷-
êè). Ïîä äåéñòâèåì ýòèõ ñèë òà÷êà äâèæåòñÿ ñ ïîñòîÿí-
íîé ñêîðîñòüþ, ò. å.
a
H
= 0.
Óðàâíåíèå âòîðîãî çàêîíà Íüþòîíà èìååò âèä:
m
g
H
+
R
H
+
f
H
+
F
KH
= 0.
Çàïèøåì åãî â ïðîåêöèÿõ íà îñè X è Y:
mg
x
+ R
x
+ f
x
+ F
x
= 0,
mg
y
+ R
y
+ f
y
+ F
y
= 0.
Äëÿ ñëó÷àÿ, èçîáðàæåííîãî íà ðèñ. 199, à, ýòè óðàâ-
íåíèÿ ìîæíî ïåðåïèñàòü òàê:
f = F cos α, mg + R + F sin α = 0.
(Ìû ó÷ëè, ÷òî mg
x
= 0, mg
y
= mg, R
x
= 0, R
y
= R,
f
x
= f, f
y
= 0, F
x
= F cos α, F
y
= F sin α.)
Ñëåäîâàòåëüíî,
R = mg F sin α.
Òàê êàê ñèëà íîðìàëüíîãî äàâëåíèÿ òà÷êè íà äîðîãó
ä1
F
KH
ðàâíà ïî ìîäóëþ ñèëå ðåàêöèè
R
KKH
, òî
ä1
F
= mg F sin α.
F
F
f
f
R
R
mg
mg
F
x
x
F
y
F
y
C
C
O
O
YY
X
X
à) á)
F
Ðèñ. 199
#
Äëÿ ñëó÷àÿ, èçîáðàæåííîãî íà ðèñ. 199, á, èç óðàâíå-
íèÿ âòîðîãî çàêîíà Íüþòîíà, çàïèñàííîãî äëÿ ìîäóëåé
ñèë, ïîëó÷àåì:
R = mg + F sin α.
Ñëåäîâàòåëüíî, F
ä2
= mg + F sin α.
Òàê êàê F
ä2
> F
ä1
, òî âî âòîðîì ñëó÷àå ÷åëîâåêó íóæíî
áóäåò ïðåîäîëåâàòü áîRëüøóþ ñèëó òðåíèÿ f = µF
ä2
.
79. Óñêîðåíèå âàãîíåòêè âî âðåìÿ òîðìîæåíèÿ ðàâíî
a =
0
v
t
è íàïðàâëåíî ââåðõ âäîëü óêëîíà äîðîãè. Íà âà-
ãîíåòêó äåéñòâóþò ñëåäóþùèå ñèëû: ñèëà òÿæåñòè m
g
H
,
ñèëà óïðóãîñòè êàíàòà
F
KH
, ñèëà ðåàêöèè îïîðû
R
H
è ñèëà
òðåíèÿ
f
H
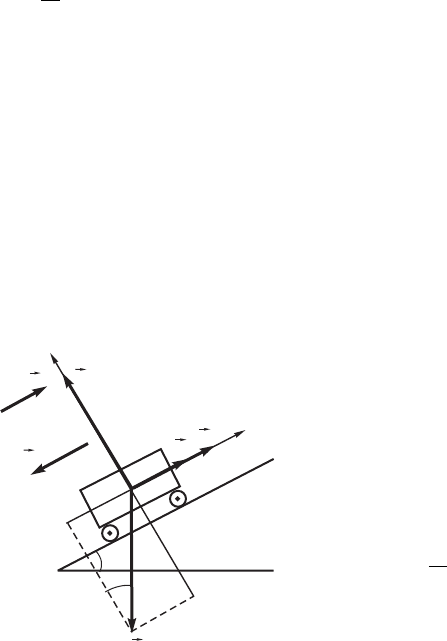
(ðèñ. 200).
 ñîîòâåòñòâèè ñî âòîðûì çàêîíîì Íüþòîíà
m
g
H
+
F
KH
+
R
H
+
f
H
= m
a
H
. (1)
Ïðîâåäåì îñè X è Y òàê, êàê ïîêàçàíî íà ðèñ. 200, è
çàïèøåì âûðàæåíèå (1) â ïðîåêöèÿõ íà ýòè îñè ñ ó÷åòîì
çíàêîâ è çíà÷åíèé ïðîåêöèé.
Íà îñü X: f + F mg sin α = ma; (2)
íà îñü Y:
mg cos α + R = 0. (3)
Èç ñîîòíîøåíèÿ (2)
âûðàçèì F:
F = mg sin α f + ma,
ãäå f = µF
ä
, íî F
ä
= R, è
a =
0
v
t
.
Èç óðàâíåíèÿ (3) âûðà-
çèì R:
R = mg cos α.
F
f
a
v
mg
X
Y
0
R
Ðèñ. 200
#!
Îêîí÷àòåëüíî äëÿ F ïîëó÷èì:
F = m(a + g sin α) µ mg cos α; F ≈ 2,6 êÍ.
Òàê êàê T = F (òðåòèé çàêîí Íüþòîíà), òî T ≈ 2,6 êÍ.
80. Ïðè âúåçäå íà íàêëîííóþ ïëîñêîñòü òåëåæêà ïðè-
îáðåòåò óñêîðåíèå
a
H
, íàïðàâëåííîå â ñòîðîíó, ïðîòèâî-
ïîëîæíóþ åå äâèæåíèþ. Òî÷êà ïîäâåñà, äâèãàÿñü çàìåä-
ëåííî, îòñòàíåò îò øàðèêà. Óñêîðåíèå øàðèêà ñòàíåò
ðàâíûì óñêîðåíèþ òåëåæêè â òîò ìîìåíò, êîãäà íèòü,
óäåðæèâàþùàÿ øàðèê, áóäåò íàïðàâëåíà ïåðïåíäèêóëÿð-
íî ê íàêëîííîé ïëîñêîñòè (ñì. ðåøåíèå çàäà÷è 76).
§ 6. Èìïóëüñ. Çàêîí ñîõðàíåíèÿ èìïóëüñà
81. Èçìåíåíèå èìïóëüñà øàðèêà ïðè óäàðå î ñòåíêó
ðàâíî ïðîèçâåäåíèþ ñèëû, äåéñòâóþùåé íà øàðèê, íà
âðåìÿ åå äåéñòâèÿ:
m
2
v
H
m
1
v
H
=
F
KH
t,
ãäå m
1
v
H
è m
2
v
H
èìïóëüñû øàðèêà äî è ïîñëå óäàðà.
Òàê êàê â ðåçóëüòàòå óäàðà èìïóëüñ øàðèêà èçìåíèë
íàïðàâëåíèå íà ïðîòèâîïîëîæíîå, ñîõðàíèâ ìîäóëü
(
2
v
H
=
1
v
H
=
v
H
), òî èçìåíåíèå èìïóëüñà øàðèêà ðàâíî
2m
v
H
è íàïðàâëåíî îò ñòåíêè, ò. å.
F
KH
t = 2m
v
H
. Ìîäóëü
ñèëû äåéñòâèÿ øàðèêà íà ñòåíêó F =
2
mv
t
.
82.
F
KH
t = m
v
H
.
Ó ê à ç à í è å. Ñêîðîñòü øàðèêà ïîñëå óäàðà v
2
= 0 (ñì.
ðåøåíèå çàäà÷è 81).
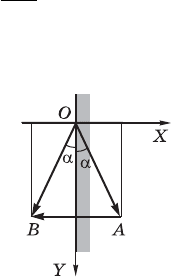
83. Åñëè âåêòîð
OA
KKK H
èìïóëüñ øà-
ðèêà äî óäàðà, âåêòîð
OB
KKK H
ïîñëå óäà-
ðà (ðèñ. 201), òî âåêòîð
AB
KKKKH
îïðåäåëÿ-
åò èçìåíåíèå èìïóëüñà øàðèêà. Åñëè
ðàññìîòðåòü ïðîåêöèè âåêòîðîâ
OA
KKK H
è
OB
KKKH
íà îñè, ïåðïåíäèêóëÿðíóþ (OX) è
ïàðàëëåëüíóþ (OY) ñòåíêå, òî èç ðàâåí- Ðèñ. 201

#"
ñòâà óãëîâ α è ðàâåíñòâà ìîäóëåé âåê-
òîðîâ
OA
KKK H
è
OB
KKK H
ñëåäóåò, ÷òî èçìåíåíèå
èìïóëüñà øàðèêà
mv∆
H
ïðîèñõîäèò òîëü-
êî çà ñ÷åò èçìåíåíèÿ ïðîåêöèè, ïåðïåí-
äèêóëÿðíîé ê ñòåíêå (îíà èçìåíÿåò
çíàê), ò.å. îíî ðàâíî ïî ìîäóëþ 2mv sin α
è íàïðàâëåíî îò ñòåíêè.
84. Èìïóëüñ
p
H
ñèñòåìû øàðèêîâ èçîáðàçèòñÿ âåêòî-
ðîì
OC
KKKH
(ðèñ. 202), ñîñòàâëÿþùèì óãîë α = 45° ñ âåêòî-
ðàìè
OA
KKK H
è
OB
KKK H
, è ðàâåí ïî ìîäóëþ p =
22
11 22
()()
mv mv+
=
= 0,017 êã ì/ñ.
85. m =
Ft
v∆
= 9,8 êã.
86. Ñèëà òÿãè
F
KH
òåïëîâîçà çà âðåìÿ t èçìåíÿåò èì-
ïóëüñ ïîåçäà íà âåëè÷èíó
F
KH
t, à ñèëà òðåíèÿ íà âåëè-
÷èíó
f
H
t (ft = µmgt). Ñîãëàñíî âòîðîìó çàêîíó Íüþòîíà
Ft µmgt = mv; îòñþäà F =
mv
t
+ µmg; F = 999,6 êÍ.
87. Ñèëà íîðìàëüíîãî äàâëåíèÿ òåëà íà ïëîñêîñòü
F
ä
= R = mg cos α; ñèëà òðåíèÿ f = µF
ä
= µmg cos α.
Ïðîåêöèÿ ñèëû òÿæåñòè íà îñü X, íàïðàâëåííóþ âäîëü
íàêëîííîé ïëîñêîñòè ê åå îñíîâàíèþ, ðàâíà mg sin α.
Ñîãëàñíî âòîðîìó çàêîíó Íüþòîíà
(mg sin α µmg cos α)t = mv, (1)
ãäå v ñêîðîñòü òåëà â êîíöå ñïóñêà è t âðåìÿ ñïóñêà.
Òàê êàê íà÷àëüíàÿ ñêîðîñòü v
0
= 0, òî l =
2
2
at
=
2
vt
;
îòñþäà v =
2
l
t
. Ïîäñòàâëÿÿ çíà÷åíèå v â óðàâíåíèå (1),
íàéäåì
t =
2
(sin cos )
l
g α−µ α
≈ 1 c. (2)
Ðèñ. 202

##
88. Ñèëà
F
KH
, ñ êîòîðîé ÷åëîâåê òÿíåò âåðåâêó, èçìå-
íÿåò èìïóëüñû ëîäîê íà âåëè÷èíó
F
KH
t (Ft = 250 êãì/c).
Ïåðâàÿ ëîäêà çà ñ÷åò ýòîãî ïðèîáðåòàåò ñêîðîñòü îòíîñè-
òåëüíî áåðåãà v
1
=
1
Ft
m
= 1 ì/ñ, à âòîðàÿ ëîäêà ñêîðîñòü
v
2
=
2
Ft
m
= 0,5 ì/ñ. Ñêîðîñòü ïåðâîé ëîäêè îòíîñèòåëüíî
âòîðîé è = v
1
+ v
2
= 1,5 ì/ñ.
Çàäà÷ó ìîæíî òàêæå ðåøèòü, ðàññ÷èòûâàÿ ïî âòîðî-
ìó çàêîíó Íüþòîíà óñêîðåíèÿ ëîäîê, à çàòåì ïî ôîðìó-
ëàì ðàâíîóñêîðåííîãî äâèæåíèÿ ñêîðîñòè.
89. Òàê êàê èìïóëüñ ñèñòåìû ÷åëîâåê àýðîñòàò äî
íà÷àëà äâèæåíèÿ ÷åëîâåêà ðàâåí íóëþ, òî ïðè ïåðåìå-
ùåíèè ÷åëîâåêà ââåðõ àýðîñòàò äîëæåí íà÷àòü îïóñêàòü-
ñÿ ñ òàêîé ñêîðîñòüþ v
1
, ÷òîáû èìïóëüñ ñèñòåìû ÷åëîâåê
àýðîñòàò ïî-ïðåæíåìó îñòàâàëñÿ ðàâíûì íóëþ.
Ñêîðîñòü äâèæåíèÿ ÷åëîâåêà îòíîñèòåëüíî Çåìëè
v
2
= è v
1
. Èìïóëüñ ÷åëîâåêà ðàâåí m
2
v
2
, èìïóëüñ àýðî-
ñòàòà ðàâåí m
1
v
1
è èìïóëüñ ñèñòåìû ÷åëîâåê àýðîñòàò
m
2
(u v
1
) m
1
v
1
= 0; îòñþäà v
1
=
2
12
mu
mm+
.
90. Öåíòð ìàññ òåëåæåê ïåðåä íà÷àëîì äâèæåíèÿ ëå-
æèò íà ïðÿìîé ÎÎ (ðèñ. 203). Ïî îïðåäåëåíèþ öåíòðà
ìàññ ðàññòîÿíèÿ îò òåëåæåê l
1
è l
2
äî öåíòðà ìàññ ñèñòå-
ìû â ëþáîé ìîìåíò âðåìåíè t äîëæíû áûòü îáðàòíî ïðî-
ïîðöèîíàëüíû èõ ìàññàì:
1
2
l
l
=
2
1
m
m
.
Ïóòè, ïðîéäåííûå òåëåæêàìè çà âðåìÿ t:
s
1
= v
1
t, s
2
= v
2
t,
ò.å.
11
22
sv
sv
=
.
Ñîãëàñíî çàêîíó ñîõðàíå-
íèÿ èìïóëüñà ñêîðîñòè, ïî-
ëó÷åííûå òåëåæêàìè çà ñ÷åò
Ðèñ. 203
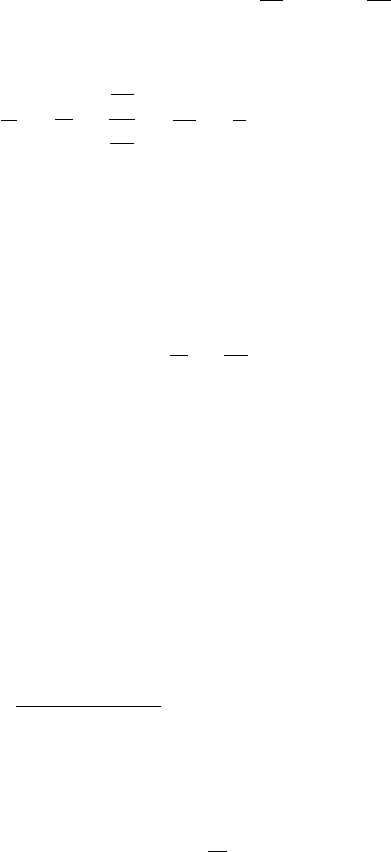
#$
äåéñòâèÿ ñæàòîé ïðóæèíû, ðàâíû v
1
=
1
Ft
m
è v
2
=
2
Ft
m
,
ñëåäîâàòåëüíî,
1
2
s
s
=
1
2
v
v
=
1
2
Ft
m
Ft
m
=
2
1
m
m
=
1
2
l
l
.
Ðàññòîÿíèÿ îò òåëåæåê äî ïðÿìîé ÎÎ óäîâëåòâîðÿ-
þò òîìó æå ñîîòíîøåíèþ, ÷òî è ðàññòîÿíèÿ äî öåíòðà
ìàññ, ò. å. öåíòð ìàññ òåëåæåê âñå âðåìÿ îñòàåòñÿ íà
ïðÿìîé OO.
Ýòîò æå ðåçóëüòàò íåïîñðåäñòâåííî ïîëó÷àåòñÿ èç çà-
êîíà ñîõðàíåíèÿ èìïóëüñà:
m
1
v
1
= m
2
v
2
, èëè
1
2
v
v
=
2
1
m
m
.
91. Ñóììû èìïóëüñîâ îñêîëêîâ ãðàíàòû äî è ïîñëå
ðàçðûâà ðàâíû ñîîòâåòñòâåííî (m
1
+ m
2
)
u
H
è m
1
1
v
H
+
+ m
2
2
v
H
. Òàê êàê èçìåíåíèå èìïóëüñîâ îñêîëêîâ ãðàíàòû
ïðîèçîøëî òîëüêî çà ñ÷åò âíóòðåííèõ ñèë, òî ñîãëàñíî
çàêîíó ñîõðàíåíèÿ èìïóëüñà â ïðîåêöèÿõ íà îñü X, ñîâ-
ïàäàþùóþ ñ íàïðàâëåíèåì äâèæåíèÿ ãðàíàòû, áóäåì
èìåòü:
(m
1
+ m
2
)u = m
1
v
1x
+ m
2
v
2
.
Ïðè íàïèñàíèè ýòîãî óðàâíåíèÿ ìû ó÷ëè, ÷òî u
x
= u
è v
2x
= v
2
. Îòñþäà
v
1x
=
12 22
1
()
mmumv
m
+−
= 12,5 ì/ñ.
Çíàê «» ó ïðîåêöèè ñêîðîñòè ïîêàçûâàåò, ÷òî ïîñëå
ðàçðûâà ìåíüøèé îñêîëîê ãðàíàòû ñòàë äâèãàòüñÿ â ñòîðî-
íó, ïðîòèâîïîëîæíóþ íàïðàâëåíèþ äâèæåíèÿ ãðàíàòû.
92. Äàëüíîñòü ïîëåòà ðàêåòû s =
2
1
v
g
sin 2α (ñì. ðåøå-
íèå çàäà÷è 40). Íà÷àëüíàÿ ñêîðîñòü ðàêåòû îïðåäåëÿåò-
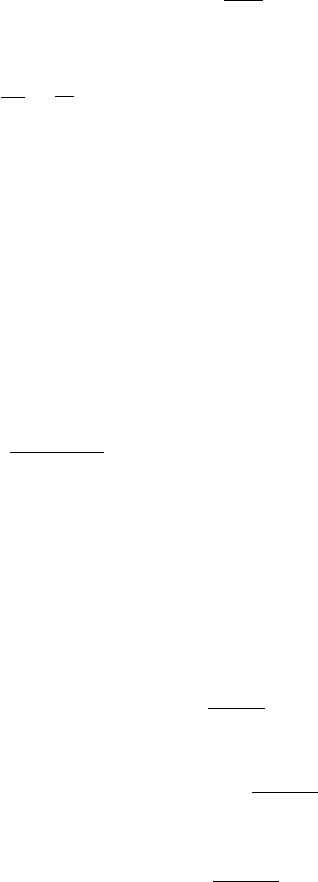
#%
ñÿ èç çàêîíà ñîõðàíåíèÿ èìïóëüñà: v
1
=
22
1
mv
m
. Ïîäñòàâ-
ëÿÿ çíà÷åíèå v
1
â ôîðìóëó äëÿ s, èìååì
s =
2
2
1
m
m
2
2
v
g
sin 2α = 360 ì.
93. Ñóììû èìïóëüñîâ øàðà è òåëåæêè äî è ïîñëå âñòðå-
÷è ðàâíû m
2
2
v
H
+ m
1
1
v
H
è (m
2
+ m
1
)
u
H
. Ñîãëàñíî çàêîíó
ñîõðàíåíèÿ èìïóëüñà
m
2
2
v
H
+ m
1
1
v
H
= (m
2
+ m
1
)
u
H
.
Çàïèøåì ýòî óðàâíåíèå â ïðîåêöèÿõ íà îñü X, íà-
ïðàâëåííóþ ñëåâà íàïðàâî, ïðè ýòîì ó÷òåì, ÷òî v
2x
= v
2
,
v
1x
= v
1
:
m
2
v
2
m
1
v
1
= (m
2
+ m
1
)u
x
.
Îòñþäà
u
x
=
22 11
21
mv mv
mm
−
+
= 0,33 ì/ñ.
Ïðîåêöèÿ u
x
ïîëîæèòåëüíà, ñëåäîâàòåëüíî, òåëåæêà
ïîêàòèòñÿ âïðàâî,
94. Îáîçíà÷èì ÷åðåç v
1
ñêîðîñòü ðàêåòîïëàíà ïîñëå
âûáðîñà ïåðâîé ïîðöèè ãàçà, v
2
ïîñëå âûáðîñà âòîðîé
ïîðöèè, v
3
ïîñëå âûáðîñà òðåòüåé è v
N
ïîñëå âûáðîñà
N-é ïîðöèè. Ïîëüçóÿñü çàêîíîì ñîõðàíåíèÿ èìïóëüñà,
ïîëó÷èì äëÿ ñêîðîñòåé ðàêåòîïëàíà:
ïîñëå âûáðîñà ïåðâîé ïîðöèè ãàçà
(M m)v
1
mu = 0, èëè v
1
=
mu
Mm−
;
ïîñëå âûáðîñà âòîðîé ïîðöèè ãàçà
(M m)v
1
= (M 2m)v
2
mu, èëè v
2
=
2
2
mu
Mm−
;
ïîñëå âûáðîñà òðåòüåé ïîðöèè ãàçà
(M 2m)v
2
= (M 3m)v
3
mu, èëè v
3
=
3
3
mu
Mm−
≈ 2 ì/ñ.
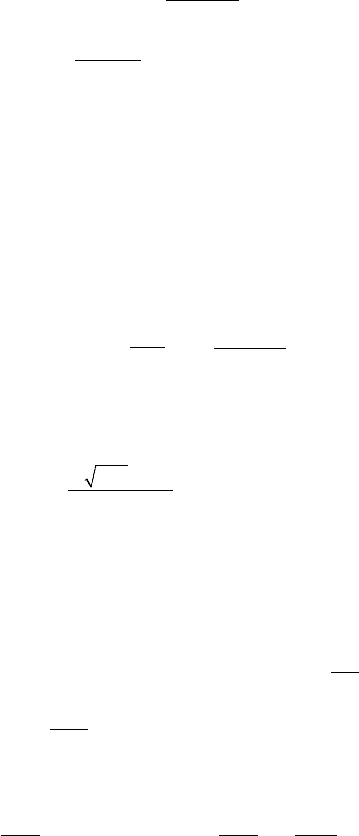
#&
Äëÿ ñêîðîñòè ðàêåòîïëàíà ïîñëå N-ãî âçðûâà áóäåì
èìåòü
v
N
=
Nmu
MNm−
≈ 13,5 ì/ñ.
95. v
2
=
2
2
mu
Mm−
≈ 1 ì/ñ (ñì. ðåøåíèå çàäà÷è 94).
96. Ïðè îïðåäåëåíèè ñêîðîñòè îòêàòà îðóäèÿ ñëåäóåò
ó÷èòûâàòü òîëüêî ïðîåêöèþ ñêîðîñòè ñíàðÿäà íà ãîðè-
çîíòàëüíîå íàïðàâëåíèå, òàê êàê îòäà÷à, îáóñëîâëåííàÿ
âåðòèêàëüíîé ïðîåêöèåé ýòîé ñêîðîñòè, áóäåò ïîãàøåíà
ñèëàìè ðåàêöèè ïîâåðõíîñòè Çåìëè.
Ãîðèçîíòàëüíàÿ ïðîåêöèÿ ñêîðîñòè ñíàðÿäà u
x
= u cos α.
Ñîãëàñíî çàêîíó ñîõðàíåíèÿ èìïóëüñà
0 = Mv
x
+ mu
x
.
Îòñþäà
v
x
=
x
mu
M
=
cos
mu
M
α
≈ 3,5 ì/ñ.
Çíàê «» ó ïðîåêöèè îçíà÷àåò, ÷òî ñêîðîñòü îòêàòà
v
H
íàïðàâëåíà ïðîòèâîïîëîæíî âûáðàííîìó íàïðàâëåíèþ
îñè X.
97. v =
2cos
mgh
mM
α
+
(ñì. ðåøåíèå çàäà÷è 96).
§ 7. Ðàáîòà. Ýíåðãèÿ. Ìîùíîñòü. Çàêîí
ñîõðàíåíèÿ ýíåðãèè
98. Ñêîðîñòü ñòâîëà v â ìîìåíò âûñòðåëà îïðåäåëèòñÿ
èç çàêîíà ñîõðàíåíèÿ èìïóëüñà: v =
mu
M
. Êèíåòè÷åñêàÿ
ýíåðãèÿ
2
2
Mv
, ïîëó÷åííàÿ ñòâîëîì â ìîìåíò âûñòðåëà,
ïîëíîñòüþ áóäåò èçðàñõîäîâàíà íà ðàáîòó ïî ïðåîäîëåíèþ
ñèëû òîðìîæåíèÿ: À = fs, ò.å. áóäåò èìåòü ìåñòî ðàâåíñòâî
2
2
Mv
= fs; îòñþäà f =
2
2
Mv
s
=
22
2
mu
Ms
; f = 12,5 êÍ.
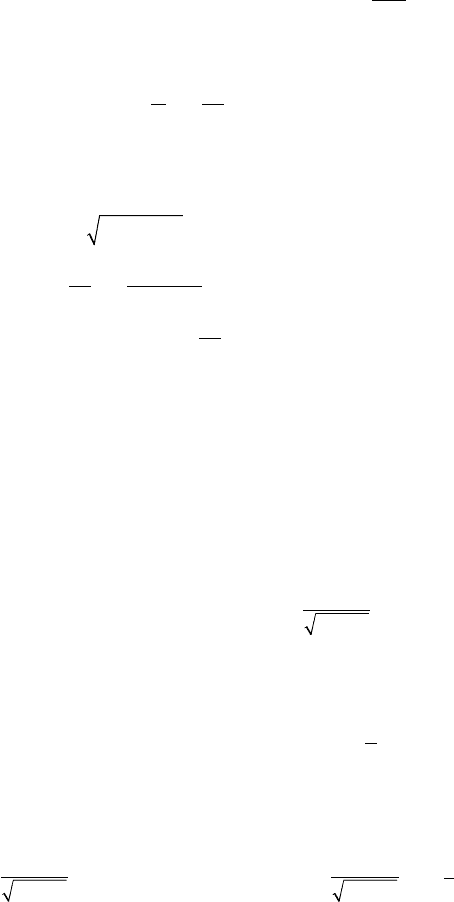
#'
99. Ýíåðãèÿ òåëà â êîíöå ïàäåíèÿ E =
2
0
2
mv
+ mgH.
Ñðåäíÿÿ ñèëà ñîïðîòèâëåíèÿ ïî÷âû îïðåäåëèòñÿ èç çà-
êîíà ñîõðàíåíèÿ ýíåðãèè:
fh = E; îòñþäà f =
E
h
=
2
m
h
(
2
0
v
+ 2gH); f = 12,25 êÍ.
Çàäà÷à ìîæåò áûòü òàêæå ðåøåíà ïóòåì ïðÿìîãî ïðè-
ìåíåíèÿ âòîðîãî çàêîíà Íüþòîíà è ðàñ÷åòà óñêîðåíèé
òåëà ïðè óãëóáëåíèè â ïî÷âó. Ñêîðîñòü òåëà ó ïîâåðõíî-
ñòè çåìëè v =
2
0
2
vgH+
. Óñêîðåíèå ïðè äâèæåíèè òåëà
â ïî÷âå a =
2
2
v
h
=
2
0
2
2
vgH
h
+
. Ñèëà ñîïðîòèâëåíèÿ ïî÷âû
f = ma =
2
m
h
(
2
0
v
+ 2gH).
Òàê êàê ñèëà òÿæåñòè mg ìàëà ïî ñðàâíåíèþ ñ ñèëîé
ñîïðîòèâëåíèÿ f, òî â ðåøåíèè íå ó÷èòûâàåòñÿ åå äåé-
ñòâèå ïðè äâèæåíèè òåëà â ïî÷âå.
100. Ñàíè, íàõîäÿñü íà âåðøèíå ãîðû, îáëàäàþò ïî-
òåíöèàëüíîé ýíåðãèåé, ðàâíîé mgh. Ýòà ýíåðãèÿ ïðè äâè-
æåíèè ðàñõîäóåòñÿ íà ðàáîòó A
1
ïî ïðåîäîëåíèþ ñèëû
òðåíèÿ íà ó÷àñòêå ÎB è íà ðàáîòó À
2
ïî ïðåîäîëåíèþ
ñèëû òðåíèÿ íà ó÷àñòêå ÂÑ:
mgh = A
1
+ A
2
.
Äëÿ ó÷àñòêà OB ñèëà òðåíèÿ f
1
=
22
mgl
lh
µ
+
, ãäå l äëè-
íà îòðåçêà AB, è ðàáîòà A
1
= f
1
OB = µmgl. Äëÿ ó÷àñòêà
BC ñèëà òðåíèÿ f
2
= µmg è ðàáîòà A
2
= f
2
BC =
= µmg(s l); îòñþäà
mgh = A
1
+ A
2
= µmgs, ò.å. µ =
h
s
.
Óðàâíåíèå âòîðîãî çàêîíà Íüþòîíà äëÿ äâèæåíèÿ ñà-
íåé íà ó÷àñòêå Πâ ïðîåêöèÿõ íà îñü X, íàïðàâëåííóþ
âäîëü íàêëîííîé ïëîñêîñòè ê åå îñíîâàíèþ, èìååò âèä:
mg
22
h
lh+
f
1
= ma
1x
; îòñþäà a
1x
=
22
gh
lh+
1
l
s
−
.

$
Òàê êàê
l
s
< 1, òî a
1x
> 0 ñàíè äâèæóòñÿ ðàâíîóñêîðåííî.
Äëÿ ó÷àñòêà BC (îñü X íàïðàâëåíà ñëåâà íàïðàâî) óðàâ-
íåíèå âòîðîãî çàêîíà Íüþòîíà èìååò âèä: f
2
= ma
2x
.
Òàê êàê f
2
= µmg, òî a
2x
= µg. Çíàê «» ó ïðîåêöèè
óñêîðåíèÿ îçíà÷àåò, ÷òî íà ó÷àñòêå BC ñàíè äâèæóòñÿ
ðàâíîçàìåäëåííî.
101. Ïðè òîì æå êîýôôèöèåíòå òðåíèÿ µ ðàññòîÿíèå s
íå áóäåò ìåíÿòüñÿ ñ óìåíüøåíèåì íàêëîíà ãîðû.
Ñàíè äâèãàòüñÿ íå áóäóò. Ïðè òàêîì óãëå íàêëîíà
tg α =
h
s
= µ, è ñèëà òðåíèÿ ïî ìîäóëþ áóäåò ðàâíà
ïðîåêöèè ñèëû òÿæåñòè íà îñü, íàïðàâëåííóþ âäîëü íà-
êëîííîé ïëîñêîñòè ê åå îñíîâàíèþ.
102. Ïîòåíöèàëüíàÿ ýíåðãèÿ ïàðàëëåëåïèïåäà, îïðå-
äåëÿåìàÿ âûñîòîé, íà êîòîðîé ðàñïîëîæåí öåíòð ìàññ, â
ðàçëè÷íûõ ïîëîæåíèÿõ ðàâíà: 2mgl, êîãäà îí ëåæèò íà
ìåíüøåé ãðàíè; mgl, êîãäà îí ëåæèò íà ñðåäíåé ãðàíè;
2
mgl
, êîãäà îí ëåæèò íà áîëüøåé ãðàíè. Íàèáîëåå óñòîé-
÷èâûì ïîëîæåíèåì, ñîîòâåòñòâóþùèì ìèíèìàëüíîé ïî-
òåíöèàëüíîé ýíåðãèè òåëà, áóäåò ïîñëåäíåå.
103. Ðàáîòà, ñîâåðøàåìàÿ ñèëîé ñîïðîòèâëåíèÿ âîç-
äóõà, ðàâíà èçìåíåíèþ êèíåòè÷åñêîé ýíåðãèè ïóëè:
A =
2
2
mv
2
0
2
mv
=
2
m
(v
2
2
0
v
); A = 3,75 êÄæ.
Òàê êàê ðàáîòà îòðèöàòåëüíà, òî ñîâåðøàëàñü îíà çà
ñ÷åò óáûëè êèíåòè÷åñêîé ýíåðãèè òåëà.
104.  ïåðâîì ñëó÷àå ìàëü÷èê ïðè áðîñàíèè êàìíÿ
ñîâåðøàåò ðàáîòó
2
1
2
mv
. Åñëè âî âòîðîì ñëó÷àå ñèëà, äåé-
ñòâóþùàÿ íà êàìåíü, òà æå, òî îí ñîâåðøàåò òàêóþ æå
ðàáîòó, íî çà åå ñ÷åò êèíåòè÷åñêóþ ýíåðãèþ ïðèîáðåòà-
þò êàìåíü è ìàëü÷èê:
2
1
2
mv
=
2
2
2
mv
+
2
2
Mu
, (1)
