Зубов В.Г., Шальнов В.П. Сборник задач по физике
Подождите немного. Документ загружается.


"
50. v ≈ 7,9 êì/ñ.
Ó ê à ç à í è å. Ïðè çàäàííûõ â
çàäà÷å óñëîâèÿõ öåíòðîñòðåìèòåëü-
íîå óñêîðåíèå ïðè äâèæåíèè òåëà
âîêðóã Çåìëè äîëæíî áûòü ðàâíî óñ-
êîðåíèþ ñâîáîäíîãî ïàäåíèÿ.
51. Öåíòð âðàùåíèÿ Î ëåæèò íà
ðàññòîÿíèè x = 62,5 ñì îò ëèíèè ÀÂ è
íà ðàññòîÿíèè y = 12,5 ñì îò ëèíèè AD.
Ó ê à ç à í è å. Ïðè ïîâîðîòå êðûøêè ñòîëà èç ïîëî-
æåíèÿ ABCD â ïîëîæåíèå A
1
B
1
C
1
D
1
(ðèñ. 190) òî÷êà À
ïåðåõîäèò â òî÷êó A
1
, òî÷êà  â òî÷êó B
1
è ò. ä. Ëèíèè
AA
1
è BB
1
áóäóò õîðäàìè äóã, ïî êîòîðûì ïåðåìåùàþòñÿ
òî÷êè À è  âî âðåìÿ ïîâîðîòà êðûøêè. Öåíòð âðàùå-
íèÿ áóäåò ëåæàòü â òî÷êå ïåðåñå÷åíèÿ ïåðïåíäèêóëÿðîâ,
ïðîâåäåííûõ èç ñåðåäèí ýòèõ õîðä.
§ 5. Äèíàìèêà ïðÿìîëèíåéíîãî äâèæåíèÿ
òåëà. Âòîðîé çàêîí Íüþòîíà
52. F =
2
2
ms
t
; F = 12,5 ìÍ.
53. Åñëè ñèëà íîðìàëüíîãî äàâëåíèÿ êàìíÿ
H
g
F
. Ýòà
ñèëà ïî ìîäóëþ ðàâíà ñèëå òÿæåñòè, äåéñòâóþùåé íà
òåëî: F
g
= mg), òî ñèëà òðåíèÿ f = µF
g
= µmg. Óñêîðåíèå,
ïðèîáðåòåííîå êàìíåì ïîä äåéñòâèåì ýòîé ñèëû îïðåäå-
ëèòñÿ èç óðàâíåíèÿ µmg = òà, à íà÷àëüíàÿ ñêîðîñòü
èç ñîîòíîøåíèÿ
v
0
=
2as
=
2 gs
µ
; v = 7,56 ì/ñ.
54. s =
2
0
2
v
gµ
; s = 25,6 ì (ñì. ðåøåíèå çàäà÷è 53).
55. T = ma ≈ 422 Í.
56. Òàê êàê ìîùíîñòü ìîòîðà â îáîèõ ñëó÷àÿõ îäíà è
òà æå, òî äîëæíî èìåòü ìåñòî ñîîòíîøåíèå
N = F
1
v
1
= F
2
v
2
,
Ðèñ. 190
"
ãäå F
1
è v
1
ìîäóëü ñèëû òÿãè ìîòîðà è ñêîðîñòè òÿãà÷à
ïðè äâèæåíèè ïî ëåäÿíîé äîðîãå, F
2
è v
2
ìîäóëü ñèëû
òÿãè è ñêîðîñòè òÿãà÷à ïðè äâèæåíèè ïî ëåæíåâîé äîðî-
ãå. Òàê êàê ðàáîòà ñèëû òÿãè ìîòîðà â îáîèõ ñëó÷àÿõ,
ïðè ïîñòîÿííîé ñêîðîñòè äâèæåíèÿ, ðàñõîäóåòñÿ òîëüêî
íà ïðåîäîëåíèå ñèëû òðåíèÿ, òî äîëæíî áûòü
F
1
= µ
1
F
g
, F
2
= µ
2
F
g
,
ãäå F
g
ñèëà íîðìàëüíîãî äàâëåíèÿ ñàíåé íà äîðîãó. Èç
(1) è (2) ñëåäóåò, ÷òî
µ
1
v
1
= µ
2
v
2
, ò. å. v
2
=
11
2
vµ
µ
= 1 êì/÷.
57. Åñëè áû íà òåëî äåéñòâîâàëà òîëüêî ñèëà òÿæåñòè
mg, òî îíî äâèãàëîñü áû ñ óñêîðåíèåì g = 9,8 ì/ñ
2
. Òåëî
äâèæåòñÿ ñ óñêîðåíèåì à > g, ñëåäîâàòåëüíî, íà íåãî
äåéñòâóåò, êðîìå ñèëû
mg
KKKH
, åùå íåêîòîðàÿ ñèëà, íàïðàâ-
ëåííàÿ âíèç. Ïî âòîðîìó çàêîíó Íüþòîíà
mg
KKKH
+
F
H
=
ma
KKKH
, èëè â ñêàëÿðíîé ôîðìå ñ ó÷åòîì íà-
ïðàâëåíèÿ âåêòîðîâ
g
H
,
F
H
è
a
H
:
mg + F = ma.
Îòêóäà
F = ma mg = m(a g); F = 24,5 Í.
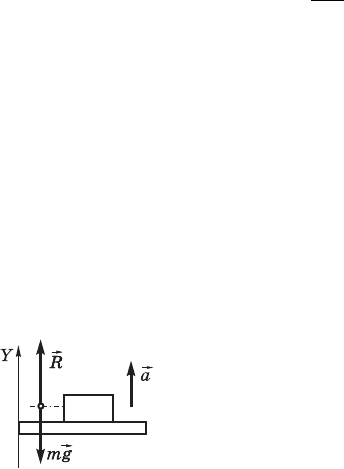
58. Ãðóç äâèæåòñÿ, òàê æå êàê è ïîä-
ñòàâêà ñ óñêîðåíèåì
a
H
. Íà ãðóç äåé-
ñòâóåò ñèëà òÿæåñòè m
g
H
(ðèñ. 191) è
ñèëà ðåàêöèè îïîðû
R
KKH
, êîòîðàÿ ïî
ìîäóëþ ðàâíà ñèëå íîðìàëüíîãî äàâ-
ëåíèÿ
KKH
ä
F
ãðóçà íà ïîäñòàâêó. Ïî âòî-
ðîìó çàêîíó Íüþòîíà, íàïèñàííîìó â ïðîåêöèÿõ íà âåð-
òèêàëüíóþ îñü, íàïðàâëåííóþ ââåðõ, áóäåì èìåòü:
R
y
+ mg
y
= ma
y
.
Íî
R
y
= R, g
y
= g, a
y
= a.
Ðèñ. 191

"!
Ñëåäîâàòåëüíî,
R mg = ma; îòñþäà F
ä
= R = m(g + a).
59. Íà øàðèê äåéñòâóþò ñèëà òÿæåñòè m
g
H
, íàïðàâ-
ëåííàÿ âåðòèêàëüíî âíèç, è ñèëà óïðóãîñòè íèòè
óïð
F
KH
.
Ïîä äåéñòâèåì ýòèõ ñèë øàðèê äâèæåòñÿ ñ óñêîðåíèåì
a
H
, íàïðàâëåíèå êîòîðîãî íåèçâåñòíî. Çàïèøåì äëÿ øà-
ðèêà âòîðîé çàêîí Íüþòîíà â ïðîåêöèÿõ íà îñü Y, íà-
ïðàâëåííóþ âåðòèêàëüíî âíèç:
mg
y
+ F
óïð y
= ma
y
. (1)
Çäåñü g
y
= g; F
óïð
y
= F
óïð
= 0,5mg (ïî óñëîâèþ çàäà÷è).
Ñ ó÷åòîì ýòîãî óðàâíåíèå (1) ïðèìåò âèä:
mg 0,5 mg = ma
y
. (2)
Îòñþäà a
y
= 0,5g = 4,9 ì/ñ
2
.
Òàê êàê ïðîåêöèÿ óñêîðåíèÿ ïîëîæèòåëüíà, òî âåê-
òîð óñêîðåíèÿ
a
H
íàïðàâëåí âåðòèêàëüíî âíèç. Ñëåäîâà-
òåëüíî, òî÷êó O íàäî ïåðåìåùàòü âåðòèêàëüíî âíèç ñ
óñêîðåíèåì a = 4,9 ì/ñ
2
.
60. Ïî ãðàôèêó (ñì. ðèñ. 11) íàõîäèì ïðîåêöèè óñêîðå-
íèÿ ëèôòà: â ïåðâûå äâå ñåêóíäû a
1y
=
1
y
v
t
= 1,8 ì/ñ
2
. Ïî
âòîðîìó çàêîíó Íüþòîíà, çàïèñàííîìó äëÿ ïðîåêöèé ñ ó÷å-
òîì èõ çíàêîâ äëÿ êàæäîãî èç òåõ ñëó÷àåâ, èìååì (ìîäóëü
ñèëû óïðóãîñòè ìû çàìåíèì ìîäóëÿìè ñèëû íàòÿæåíèÿ):
T
1
mg = ma
1
, T
2
mg = 0, T
3
mg = ma
3
,
ãäå T
1
, T
2
, T
3
ìîäóëè ñèëû íàòÿæåíèÿ êàíàòà â ñîîò-
âåòñòâóþùèå èíòåðâàëû âðåìåíè; îòñþäà
T
1
= 17,7 êÍ, T
2
= 15 êÍ, T
3
= 12,5 êÍ.
61. Íà êàæäûé èç ãðóçîâ äåéñòâóåò ñèëà
òÿæåñòè m
g
H
è ñèëà óïðóãîñòè ñî ñòîðîíû
ïðóæèíû
óïð
F
KH
(ðèñ. 192). Ïî âòîðîìó çàêîíó
Íüþòîíà
m
g
H
+
óïð
F
KH
= m
a
H
, èëè
óïð
F
KH
= m(
a
H
g
H
).
Ðèñ. 192

""
 çàâèñèìîñòè îò ìîäóëÿ è íàïðàâëåíèÿ óñêîðåíèÿ
a
H
ñèëû óïðóãîñòè áóäóò ðàçëè÷íûìè: à) åñëè ñèñòåìà ïî-
êîèòñÿ (a = 0), òî
óïð
F
KH
= m
g
H
(ñèëà óïðóãîñòè, äåéñòâóþ-
ùàÿ ñî ñòîðîíû ïðóæèíû, ðàâíà ïî ìîäóëþ ñèëå òÿæåñ-
òè, äåéñòâóþùåé íà ïðèêðåïëåííûé ê íåé ãðóç); á) åñëè
ñèñòåìà ñâîáîäíî ïàäàåò (
a
H
=
g
H
), òî
óïð
F
KH
= 0 (äåôîðìà-
öèè ïðóæèí îòñóòñòâóþò, âñå ãðóçû íàõîäÿòñÿ íà îäíîì
óðîâíå).
62. Åñëè ïàðàøþòèñò ñïóñêàåòñÿ ñ ïîñòîÿííîé ñêîðî-
ñòüþ, òî ðàâíîäåéñòâóþùàÿ âñåõ ïðèëîæåííûõ ê íåìó
ñèë ðàâíà íóëþ: m
g
H
+
f
H
= 0; èëè ñ ó÷åòîì íàïðàâëåíèÿ
ñèë, mg f = 0, ñëåäîâàòåëüíî, f = mg = 784 Í.
63. Óðàâíåíèå âòîðîãî çàêîíà Íüþòîíà äëÿ ïîäúåìà
òåëà: m
g
H
+
f
H
= m
a
H
. Åñëè îñü íàïðàâèòü âåðòèêàëüíî
ââåðõ, òî â ñêàëÿðíîé ôîðìå ýòî óðàâíåíèå ïðèìåò âèä:
f
ó
mg = ma
ó
. Èç óðàâíåíèé êèíåìàòèêè äëÿ äâèæåíèÿ ñ
êîíå÷íîé ñêîðîñòüþ v = 0 ñëåäóåò, ÷òî a
ó
=
0
v
t
; îòñþäà
f
ó
= ma
ó
+ mg = m
0
v
g
t
−+
; f
y
= 88 ìÍ.
Çíàê «» îçíà÷àåò, ÷òî ñèëà
H
f
íàïðàâëåíà ïðîòèâîïîëîæíî îñè Y,
ò. å. âåðòèêàëüíî âíèç.
 äåéñòâèòåëüíîñòè ñèëà ñîïðîòèâëåíèÿ âîçäóõà íå-
ïîñòîÿííà. Ïðè ìàëûõ ñêîðîñòÿõ îíà ïðîïîðöèîíàëüíà
ñêîðîñòè äâèæåíèÿ òåëà, ïðè áîëüøèõ ñêîðîñòÿõ îíà
âîçðàñòàåò ïðîïîðöèîíàëüíî áîëåå âûñîêèì ñòåïåíÿì
ñêîðîñòè.
64.  íà÷àëå ïðèñåäàíèÿ ÷åëîâåê ðàññëàáëÿåò ìûøöû
íîã, äàåò âîçìîæíîñòü ñâîåìó òåëó «ïàäàòü» ñ íåêîòî-
ðûì óñêîðåíèåì
a
H
, íàïðàâëåííûì âíèç, è ñèëà íîðìàëü-
íîãî äàâëåíèÿ íà ïëàòôîðìó âåñîâ
F
KH
ä
(ðàâíàÿ ïî ìîäóëþ
ñèëå ðåàêöèè îïîðû
R
H
) ñòàíîâèòñÿ òàêîé ÷òî
mg R = ma, èëè F
ä
= R = mg ma (ò. å. F
ä
< mg).
"#
(Óðàâíåíèÿ íàïèñàíû ñ ó÷åòîì íàïðàâëåíèÿ ñèë è
çíàêîâ ïðîåêöèé âåêòîðîâ.)
 êîíöå ïðèñåäàíèÿ ÷åëîâåê íàïðÿãàåò ìûøöû íîã,
óâåëè÷èâàåò ñèëó íîðìàëüíîãî äàâëåíèÿ íà ïëàòôîðìó
è òåì ñàìûì ñîçäàåò óñêîðåíèå
a
H
, íàïðàâëåííîå ââåðõ.
Ïðè ýòîì óðàâíåíèå âòîðîãî çàêîíà Íüþòîíà ïðèìåò âèä
mg R = ma, èëè F
ä
= R = mg + ma (ò. å. F
ä
> mg).
65. Óñêîðåíèå ñòîëà âî âðåìÿ ðàçãîíà: à =
v
t
= 2 ì/ñ
2
.
Óðàâíåíèå âòîðîãî çàêîíà Íüþòîíà äëÿ äâèæåíèÿ ñòîëà
âî âðåìÿ ðàçãîíà: F f = ma, ãäå f = µmg ñèëà òðåíèÿ;
îòñþäà
F = f + òà = 333,2 Í.
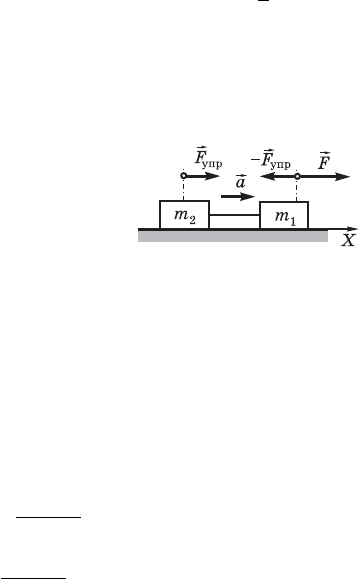
66. Äëÿ îïðåäåëåíèÿ ñèëû
íàòÿæåíèÿ
T
KH
(T = F
óïð
) íåîáõî-
äèìî çàïèñàòü óðàâíåíèÿ âòîðî-
ãî çàêîíà Íüþòîíà äëÿ êàæäîãî
èç áðóñêîâ â îòäåëüíîñòè. Íà
áðóñîê ìàññîé m
1
äåéñòâóþò ñèëû
F
KH
è
óïð
F
KH
, íà áðóñîê ìàññîé m
2
òîëüêî ñèëà
óïð
F
KH
(ðèñ.
193). Íàïðàâèì îñü X â íàïðàâëåíèè ñèëû
F
KH
è çàïèøåì
óðàâíåíèÿ âòîðîãî çàêîíà Íüþòîíà äëÿ äâóõ áðóñêîâ â
ñêàëÿðíîé ôîðìå ñ ó÷åòîì íàïðàâëåíèÿ âåêòîðîâ:
F F
óïð
= m
1
a, F
óïð
= m
2
a.
Ðåøåíèå ýòîé ñèñòåìû äàåò çíà÷åíèÿ èñêîìûõ âåëè-
÷èí:
a =
12
F
mm+
; a = 2 ì/ñ
2
,
F
óïð
=
2
12
mF
mm+
; T = F
óïð
= 0,6 Í;
à) F
max
≈ 17 Í, á) F
max
= 25 Í.
67. Ïîä äåéñòâèåì ñèëû
F
KH
âñÿ ñèñòåìà äâèæåòñÿ ñ
óñêîðåíèåì
a
H
. Óðàâíåíèÿ âòîðîãî çàêîíà Íüþòîíà äëÿ
Ðèñ. 193
"$
êàæäîãî èç áðóñêîâ â
ñêàëÿðíîé ôîðìå èìåþò
âèä:
F F
1
= ma,
F
1
F
2
= ma,
F
2
F
3
= ma,
F
3
= ma,
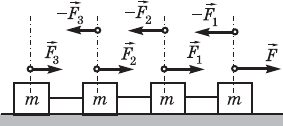
ãäå F
1
, F
2
, F
3
ìîäóëè ñèë óïðóãîñòè íèòè (ðèñ. 194).
Ðåøàÿ ýòó ñèñòåìó óðàâíåíèé, ïîëó÷èì
T
1
= F
1
= 0,75F, T
2
= F
2
= 0,5F, T
3
= F
3
= 0,25F.
68. Òÿæåëûé æåëåçíîäîðîæíûé ñîñòàâ òðóäíî ñäâè-
íóòü ñ ìåñòà, êîãäà ñöåïêè ìåæäó âàãîíàìè íàõîäÿòñÿ â
íàòÿíóòîì ñîñòîÿíèè.  ýòîì ñëó÷àå ñèëà òÿãè òåïëîâîçà
äîëæíà ñîîáùàòü óñêîðåíèå âñåìó ñîñòàâó ñðàçó. Åñëè
âíà÷àëå äàòü çàäíèé õîä, òî ñöåïêè ìåæäó âàãîíàìè áó-
äóò îñëàáëåíû è ïðè òîé æå ñèëå òÿãè òåïëîâîç ñìîæåò
ñîîáùàòü çíà÷èòåëüíî áîëüøèå óñêîðåíèÿ ñíà÷àëà áëè-
æàéøåé ê íåìó ÷àñòè ñîñòàâà, à çàòåì ïîî÷åðåäíî è âñåì
îñòàëüíûì âàãîíàì.
69. Åñëè ïåðåä íà÷àëîì äâèæåíèÿ âñå ñöåïêè â ñîñòà-
âå áûëè íàòÿíóòû, òî ðàçðûâ ìîæåò ïðîèçîéòè â ñöåï-
êàõ áëèæàéøèõ ê òåïëîâîçó âàãîíîâ. Ñèëà íàòÿæåíèÿ
ýòèõ ñöåïîê äîëæíà áûòü íàèáîëüøåé, òàê êàê îíà äîë-
æíà îáåñïå÷èâàòü ïîÿâëåíèå óñêîðåíèÿ ñðàçó ó âñåõ íà-
õîäÿùèõñÿ ñçàäè âàãîíîâ áîëüøîé ìàññû (ñì. ðåøåíèå
çàäà÷è 68).
Åñëè ïåðåä íà÷àëîì äâèæåíèÿ âñå ñöåïêè âàãîíîâ ñî-
ñòàâà ñæàòû, òî ðàçðûâ ìîæåò ïðîèçîéòè â ëþáîì ìåñòå
ñîñòàâà â çàâèñèìîñòè îò ñëó÷àéíûõ ñîîòíîøåíèé ñèë
óïðóãîñòè, âîçíèêàþùèõ â ñöåïêàõ ìåæäó îòäåëüíûìè
âàãîíàìè.
70. Âî âñåõ òðåõ ñëó÷àÿõ ñèñòåìà áóäåò äâèãàòüñÿ ñ
íåêîòîðûì óñêîðåíèåì
a
H
â ñòîðîíó äåéñòâèÿ áîëüøåé
ñèëû è äèíàìîìåòð áóäåò ïîêàçûâàòü ñèëó óïðóãîñòè F
óïð
,
äåéñòâóþùóþ ìåæäó ãðóçàìè. Äëÿ îòûñêàíèÿ ñèëû F
óïð
Ðèñ. 194

"%
íåîáõîäèìî íàïèñàòü óðàâíåíèå
âòîðîãî çàêîíà Íüþòîíà äëÿ êàæ-
äîãî ãðóçà â îòäåëüíîñòè.  ñëó÷àå
à) èìååì (ðèñ. 195):
F
1
F
óïð
= m
1
a, F
óïð
F
2
= m
2
a;
îòñþäà
a =
12
12
FF
mm
−
+
, F
óïð
= F
1
1
12
m
mm+
(F
1
F
2
).
 ñèëó òîãî, ÷òî m
2
n m
1
è
1
12
m
mm+
≈ 1, ìîæíî ñ÷è-
òàòü, ÷òî
F
óïð
≈ F
2
= 9,8 Í.
Àíàëîãè÷íî, ñîñòàâëÿÿ óðàâíåíèÿ âòîðîãî çàêîíà Íüþ-
òîíà è èñïîëüçóÿ óñëîâèÿ, âûðàæàþùèå ñîîòíîøåíèå
ìàññ, ìîæíî ðàññìîòðåòü è îñòàëüíûå ñëó÷àè:
á) F
óïð
≈ F
1
= 19,6 Í; â) F
óïð
=
12
2
FF+
= 14,7 Í.
71. Îáà ãðóçà äâèæóòñÿ ñ óñêîðåíèåì
a
H
. Íà ãðóç ìàñ-
ñîé ò
1
äåéñòâóþò ñèëà òÿæåñòè m
1
g
H
è ñèëà óïðóãîñòè
íèòè
F
KH
, íà ãðóç ìàññîé m
2
ñèëà óïðóãîñòè íèòè
F
KH
è
ñèëà òðåíèÿ
f
H
(f = µm
2
g).
Óðàâíåíèÿ âòîðîãî çàêîíà Íüþòîíà äëÿ êàæäîãî èç
ãðóçîâ â ñêàëÿðíîé ôîðìå èìåþò âèä:
m
1
g F = m
1
a, F µm
2
g = m
2
a.
Ðåøàÿ ýòó ñèñòåìó óðàâíåíèé, ïîëó÷èì
a =
12
12
mm
mm
−µ
+
g, T = F =
12
12
mm
mm+
g(1 + µ).
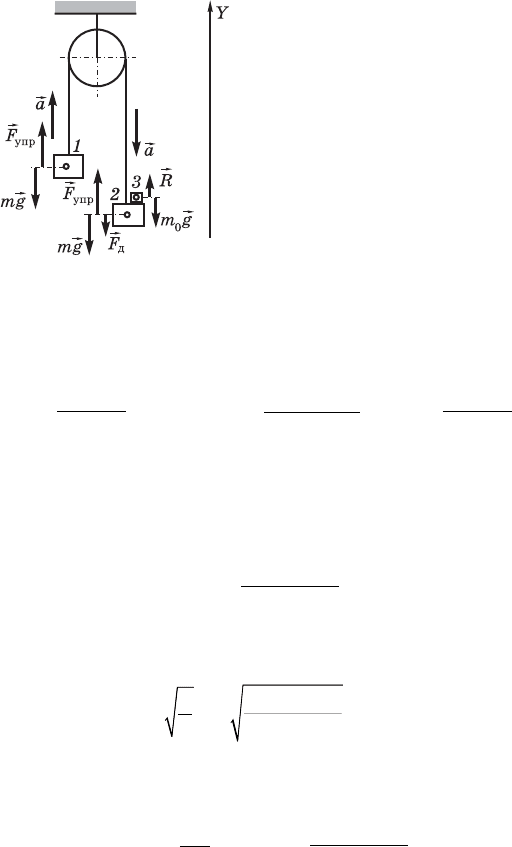
72. Âñå òåëà ñèñòåìû äâèæóòñÿ ñ óñêîðåíèåì
a
H
(ðèñ. 196).
Íà ãðóç 1 äåéñòâóþò ñèëà òÿæåñòè m
g
H
è ñèëà óïðóãîñòè
íèòè
óïð
F
KH
, íà ãðóç 2 ñèëà òÿæåñòè m
g
H
, ñèëà íîðìàëü-
íîãî äàâëåíèÿ ïåðåãðóçêà
g
F
KH
ä
è ñèëà óïðóãîñòè íèòè
óïð
F
KH
.
Ðèñ. 195
"&
Íà ïåðåãðóçîê 3 äåéñòâóþò
ñèëà òÿæåñòè m
0
g
H
è ñèëà ðå-
àêöèè
R
H
ñî ñòîðîíû ãðóçà 2,
ðàâíàÿ ïî ìîäóëþ ñèëå íîð-
ìàëüíîãî äàâëåíèÿ ïåðåãðóçêà
g
F
KH
ä
íà ãðóç 2.
Óðàâíåíèÿ âòîðîãî çàêîíà
Íüþòîíà äëÿ êàæäîãî èç òðåõ
ãðóçîâ â ïðîåêöèÿõ íà îñü Y,
íàïðàâëåííóþ âåðòèêàëüíî
ââåðõ, èìåþò âèä:
F
óïð
mg = ma, mg F
ä
+ F
óïð
= ma, m
0
g + F
ä
= m
0
a.
Ðåøåíèå ýòîé ñèñòåìû äàåò:
a =
0
0
2
m
mm+
g, T = F
óïð
=
0
0
2( )
2
mm m
mm
+
+
g, F
ä
=
0
0
2
2
mm
mm+
g.
Ñèëà äàâëåíèÿ íà îñü áëîêà ðàâíà óäâîåííîé ñèëå íà-
òÿæåíèÿ íèòè F = 2T.
73. Óñêîðåíèå
a
H
ãðóçîâ ïîëó÷èì èç óðàâíåíèé âòîðî-
ãî çàêîíà Íüþòîíà (ñì. ðåøåíèå çàäà÷è 72):
a =
21
12
()
mmg
mm
−
+
.
Âðåìÿ äâèæåíèÿ íàéäåì èç êèíåìàòè÷åñêèõ óðàâíå-
íèé ðàâíîóñêîðåííîãî äâèæåíèÿ áåç íà÷àëüíîé ñêîðîñòè:
t =
h
a
=
12
21
()
()
hm m
mmg
+
−
; t = 0,6 c.
74. ×åðåç âðåìÿ t êàæäûé èç ãðóçîâ ïåðåìåñòèòñÿ èç
íà÷àëüíîãî ïîëîæåíèÿ íà ðàññòîÿíèå
h =
2
2
at
, ãäå a =
12
12
()
mmg
mm
−
+
(ñì. ðåøåíèå çàäà÷è 72). Ïðè ýòîì öåíòð ìàññ ñèñòåìû
ãðóçîâ ñìåñòèòñÿ íà íåêîòîðîå ðàññòîÿíèå l èç ïåðâîíà-
Ðèñ. 196
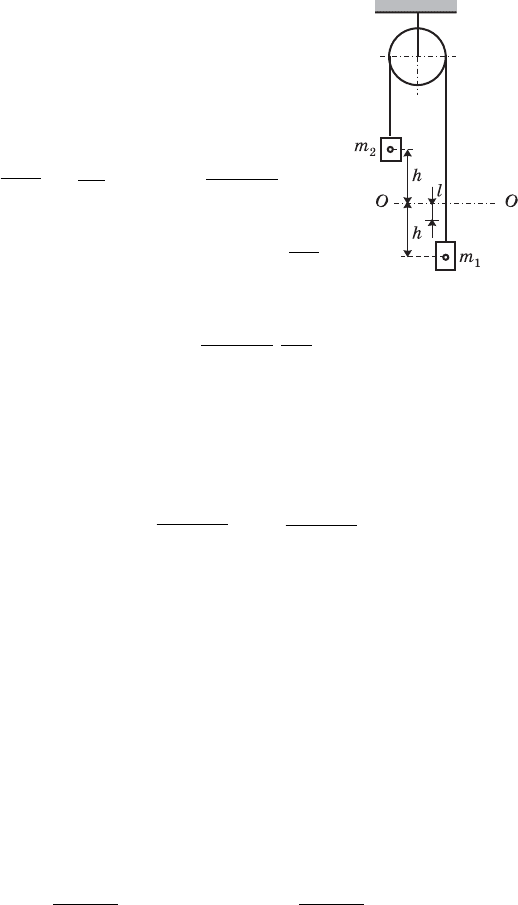
"'
÷àëüíîãî ïîëîæåíèÿ âíèç â ñòîðîíó
áîëüøåãî ãðóçà (ðèñ. 197). Òàê êàê
ðàññòîÿíèÿ îò ãðóçîâ äî öåíòðà ìàññ
ñèñòåìû äîëæíû áûòü îáðàòíî ïðî-
ïîðöèîíàëüíû ìàññàì ýòèõ ãðóçîâ,
ìîæíî çàïèñàòü:
hl
hl
+
−
=
1
2
m
m
, èëè l =
12
12
mm
mm
−
+
h.
Ïîäñòàâëÿÿ çíà÷åíèå h =
2
2
at
,
ïîëó÷èì
l =
12
12
mm
mm
−
+
2
2
at
.
Ñîïîñòàâëÿÿ ïîëó÷åííûé ðåçóëüòàò ñ ôîðìóëîé ïóòè
ðàâíîóñêîðåííîãî äâèæåíèÿ è ïîäñòàâëÿÿ çíà÷åíèå óñ-
êîðåíèÿ à ãðóçîâ, íàéäåì, ÷òî öåíòð ìàññ ñèñòåìû äîë-
æåí äâèãàòüñÿ âíèç ñ óñêîðåíèåì
a
ö.ì.
=
12
12
mm
mm
−
+
a =
−
+
2
12
12
mm
mm
g,
ò. å. óñêîðåíèå öåíòðà ìàññ ñèñòåìû ìåíüøå óñêîðåíèÿ
êàæäîãî èç ãðóçîâ â îòäåëüíîñòè.
75. à) Ìàêñèìàëüíàÿ ñèëà òðåíèÿ ïîêîÿ f = µm
0
g =
= 4,9 Í áîëüøå ñèëû F = 1,96 Í, ïðèëîæåííîé ê áðóñêó.
Ïîýòîìó ñèëà
F
KH
íå ìîæåò çàñòàâèòü áðóñîê ñêîëüçèòü ïî
òåëåæêå. Âñÿ ñèñòåìà áóäåò äâèãàòüñÿ êàê åäèíîå öåëîå ñ
îáùèì óñêîðåíèåì
a
H
, è ñèëó òðåíèÿ íóæíî îïðåäåëÿòü
èç óðàâíåíèé âòîðîãî çàêîíà Íüþòîíà äëÿ áðóñêà è òå-
ëåæêè:
F f = m
0
a, f = ma;
îòñþäà
a =
0
F
mm
+
; a = 9 ñì/ñ
2
, f =
0
mF
mm
+
; f ≈ 1,8 Í.
Ðèñ. 197
#
á) Ìàêñèìàëüíàÿ ñèëà òðåíèÿ f ìåíüøå ñèëû F. Ïî-
ýòîìó ñèëà
F
KH
âûçîâåò ñêîëüæåíèå áðóñêà ïî òåëåæêå.
Ó áðóñêà è òåëåæêè áóäóò ðàçíûå óñêîðåíèÿ
1
a
H
è
2
a
H
.
Ñèëà òðåíèÿ áóäåò èìåòü âî âðåìÿ äâèæåíèÿ ìàêñèìàëü-
íîå çíà÷åíèå f = µm
0
g = 4,9 Í. Óðàâíåíèÿ âòîðîãî çàêî-
íà Íüþòîíà äëÿ áðóñêà è òåëåæêè:
F µm
0
g = m
0
a
1
, µm
0
g = ma
2
;
îòñþäà
a
1
=
0
0
Fmg
m
−µ
; a
1
= 7,5 ì/ñ
2
, a
2
=
0
mg
m
µ
; a
2
= 0,25 ì/ñ
2
.
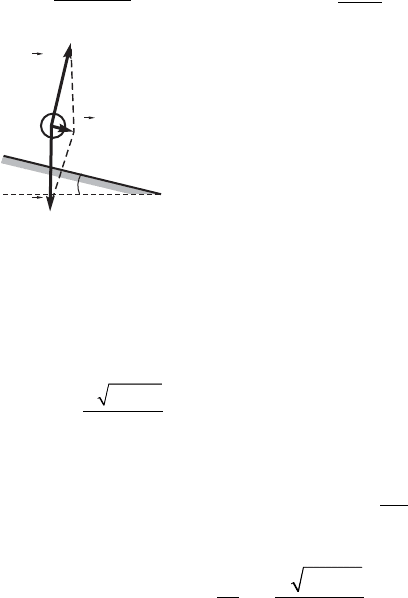
76. Òåëåæêà áóäåò ñêàòûâàòüñÿ ñ
óñêîðåíèåì, ðàâíûì ïî ìîäóëþ a =
= g sin α. Äëÿ òîãî ÷òîáû øàðèê èìåë
òàêîå æå óñêîðåíèå, íåîáõîäèìî, ÷òî-
áû ðàâíîäåéñòâóþùàÿ ñèëû òÿæåñòè
m
g
H
è ñèëû óïðóãîñòè íèòè
óïð
F
KH
, ïðè-
ëîæåííûõ ê øàðèêó (ðèñ. 198), áûëà
íàïðàâëåíà ïàðàëëåëüíî íàêëîííîé
ïëîñêîñòè è åå ìîäóëü áûë ðàâåí
F = òà òg sin α. À ýòî âîçìîæíî òîëüêî òîãäà, êîãäà
íèòü ïåðïåíäèêóëÿðíà ê íàêëîííîé ïëîñêîñòè.
77. Áðåâíî äâèæåòñÿ áåç óñêîðåíèÿ; ñëåäîâàòåëüíî, ñèëà òðå-
íèÿ ðàâíà ïî ìîäóëþ ãîðèçîíòàëüíîé ïðîåêöèè F
x
ñèëû
F
KH
,
ò. å. f =
22
Fl h
l
−
. Ñèëà íîðìàëüíîãî äàâëåíèÿ áðåâíà íà
çåìëþ
g
F
KH
ä
(ðàâíàÿ ïî ìîäóëþ ñèëå ðåàêöèè çåìëè)
F
ä
= R = mg F
ó
= mg
Fh
l
.
Êîýôôèöèåíò òðåíèÿ
µ =
ä
f
F
=
22
Fl h
mgl Fh
−
.
Èçìåíåíèå òî÷êè ïðèëîæåíèÿ ñèëû
F
KH
èçìåíÿåò ëèøü
òî÷êó ïðèëîæåíèÿ ñèëû íîðìàëüíîãî äàâëåíèÿ, íî íå
F
F
mg
óïð
m
Ðèñ. 198
