Зимина О.В., Кириллов А.И., Сальникова Т.А. Высшая математика. Решебник

Подождите немного. Документ загружается.

200 Гл.

Определенный

интеграл

вычисляется по формуле

У =

7г

[ (t;(x)2 - и{х)^) dx. (1)

Определяем область D. Если неравенства, определяюпще об-

ласть Z), неизвестны, т.е. неизвестны а и b и/или неизвестно, какая

из функций fi{x) и f2{x) больше другой на отрезке

[а,6],

то выпол-

няем следующие операции.

а) находим а и b как абсциссы точек пересечения графиков функ-

ций fi{x) и /2(2:), т.е. решаем уравнение

fi{x) = /2

(ж);

б) исследуем знак разности fi{x)

—

/2(3:) на [а,

Ь].

Для этого доста-

точно вычислить значение fi{x)

—

f2{x) в какой-нибудь точке из (а, Ь).

Если оно положительно, то fi{x) > /2(2^) и, следовательно, и{х) =

= /2(3:) и v{x) =

fi{x).

Если оно отрицательно, то /i(a;) < /2(2:) и,

следовательно, и{х) = fi{x) и v{x) = /2(2^)-

Вычисляем объем по формуле (1).

Записываем ответ, не забывая о размерности.

ЗАМЕЧАНИЕ. Аналогично решается задача, если тело образовано

вращением области вокруг оси О У или оси 0Z.

ПРИМЕР. Вычислить объем тела, образованного вращением об-

ласти, ограниченной графиками функций

у = х^ у = \/ж,

вокруг оси ох.

РЕШЕНИЕ.

Определяем область D :

а) находим абсциссы аиЬ точек пересечения графиков. Для этого

решаем уравнение

х^

= у/х.

Получаем

а = О, 6 = 1;

б) на отрезке [0,1] -Jx > х^. Следовательно, и{х)=х^ и у{х) = л/х.

8.12. Вычисление объемов тел вращения 201

Вычисляем объем по формуле (1):

У = 7Г / [(V^)2 - [x^f] dx =

f {х- X^) dx =

бтг

Ti'

Ответ. 57г/14 (ед. длины) .

Условия ЗАДАЧ. Вычислить объемы

теЛу

образованных враще-

нием вокруг оси ОХ областей, ограниченных графиками заданных

функций.

10.

= -а:2 + 1,

= х2,

у =

cos ж,

у = sin^ ж,

= е^,

у = \пх,

у = cos^ X,

= 0.

У = у/Х.

у = sin

ж,

= 0,

= 1,

у = о,

= 1,

= 0

?/ = sin (7гж/2), у = X.

у = a:^, ?/ = 2а;.

ж = 0 (0 < ж < 7г/4).

а; = 7г/2 (0<ж<7г/2).

а:=:1.

а: = е.

а; = 1.

(-7г/2

< X < 7г/2).

Ответы. 1. 1б7г/15. 2. (бтг^ - 48)/(б7г). 3. Зтг/Ю. 4. 1б7г/15.

7г2/4 - 1/2. 6. 37rVl6. 7. 7г(е2 - 4е + 5)/2. 8. 7г(е - 2).

9. 7г(3-41п2). 10. 37г78.

Глава 9

КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ

При изучении темы КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ вы по-

знакомитесь с понятиями криволинейных интегралов первого рода

(по длине дуги) и второго рода (по координатам) от функций двух и

трех переменных и научитесь вычислять их вдоль различных плоских

и пространственных кривых, заданных параметрически, в декарто-

вых и в полярных координатах, приводя криволинейные интегралы к

определенным.

С помощью пакета РЕШЕБНИК.ВМ вы можете вычислить про-

изводные функций, задающих кривую, решить системы уравнений,

определяющие граничные значения параметра, вычислить получен-

ные вами определенные интегралы и проверить правильность полу-

ченных вами результатов.

9.1.

Криволинейные интегралы

первого рода

ПОСТАНОВКА ЗАДАЧИ. Вычислить криволинейный интеграл

/ f{x,y,z)dl,

где L — часть гладкой кривощ заданной параметрически

X = a:(t),

y = y{t), ti<t<t2,

z = z{t),

и dl — дифференциал длины дуги.

9.1.

Криволинейные интегралы первого рода

203

ПЛАН РЕШЕНИЯ. Криволинейный интеграл первого рода по кри-

вой

определяется формулой

j f{x,y,z)dl

= j

f{x{t),y{t),z{t))^x'{tY + y'{tY-\-z'{tYdt.

(1)

Подчеркнем, что криволинейный интеграл первого рода

не

зависит

от направления обхода кривой

всегда

t\ <t2-

Вычисляем

x'{t), y'{t),

z'(t) и

y/x'{t)'^

y'{ty

z'{t)^

Вычисляем криволинейный интеграл по формуле (1)

записы-

ваем ответ.

ЗАМЕЧАНИЕ

Если граничные точки кривой

M{xi,yi,zi)

^{х2^У2,

Z2)

заданы

декартовых координатах, то

ti и

определяем,

решая системы уравнений

xi =x(ti), (

Х2 =x{t2),

yi = y{ti), I

2/2

2/(^2),

zi = ziti); [

2(^2).

ЗАМЕЧАНИЕ

Если кривая задана как линия пересечения двух

поверхностей:

Г Fi(x,2/,z)=0,

\ F2{x,y,z)

= 0,

то

ее

необходимо параметризовать.

ЗАМЕЧАНИЕ

Если плоская кривая задана уравнением

у = у{х)

(а

6),

то

дифференциал длины дуги равен

dl = yjl

-h

y'{xY dx

и формула (1) имеет вид

I /(х, y)dl

= I

/(х, у{х))

VI +

У\х)^ dx.

(Г)

Если плоская кривая задана

полярных координатах

{х =

gcostp,

QsiiKf) уравнением

д =

д{(р)

{а

(р

<Ь)^то дифференциал длины

дуги равен

^g{ip)''-{-g'{ipydip.

204 Гл.

Криволинейные интегралы

и формула (1) имеет вид

1 f{x,y)dl= / f{g{^) cos

V?, д{(р)

sin

(р)

у/д{(р)'^

Q'{(р^

dip.

{I")

ПРИМЕР

1. Вычислить криволинейный интеграл

х^

у^

dl,

где L — первый виток винтовой линии

X = cost,

y = smt, 0<t<27r.

z = t,

РЕШЕНИЕ.

Вычисляем: x'{t) = -sint, y'{t) = cost, z'{t) = 1, d/ =

y/2dt

Подставляем эти результаты в формулу (1) и вычисляем опре-

деленный интеграл:

27Г

Г _ 8V27r3

Ответ. / -^-—- dl =

J х^ Л-у^

L о

8\/27гЗ

ПРИМЕР

2. Вычислить криволинейный интеграл

{x~y)dl,

где L — отрезок прямой от точки

Л(0,0)

до точки

Б(4,3).

РЕШЕНИЕ.

В данном случае уравнение прямой есть у = Зж/4 (О < ж < 4)

и, следовательно, у'{х) = 3/4 и dl = 5/4

cZt.

9.1.

Криволинейные интегралы первого рода 205

Подставляем эти результаты в формулу (1') и вычисляем опре-

деленный интеграл:

1 {x-y)dl=

I (х- -жj

1^^=2'

L О

Ответ. {х - y)dl = -.

ПРИМЕР

3. Вычислить криволинейный интеграл

Г у

/ arctg

—

dl,

J X

где L — часть спирали Архимеда

—

^ (О < v^ < 7г/2).

РЕШЕНИЕ.

Вычисляем: ^'(^^) = 1, d/ = д/(/р2 -\r\d(p и f{x,y) = (/?, так как

arctg (tg

(р)

= (f при

< ip < 7г/2.

Подставляем эти результаты в формулу (1") и вычисляем опре-

деленный интеграл:

farctg^dl= /"^V^2 + ld^ = i(¥>2 +1)3/2

У^, (7г2 + 4)3/2-8

Ответ. / arctg-d/

J X 24

Условия ЗАДАЧ. Вычислить криволинейные интегралы.

/ 2/^(i/, I/ — часть кривой х = t

—

sint, у = 1

—

cost

(О < t < 27г) (ар?са циклоиды).

zdl^ L — часть кривой х = tcost, у = tsint, z = t

(О < t < 7г) {первый виток конической винт,овой линии).

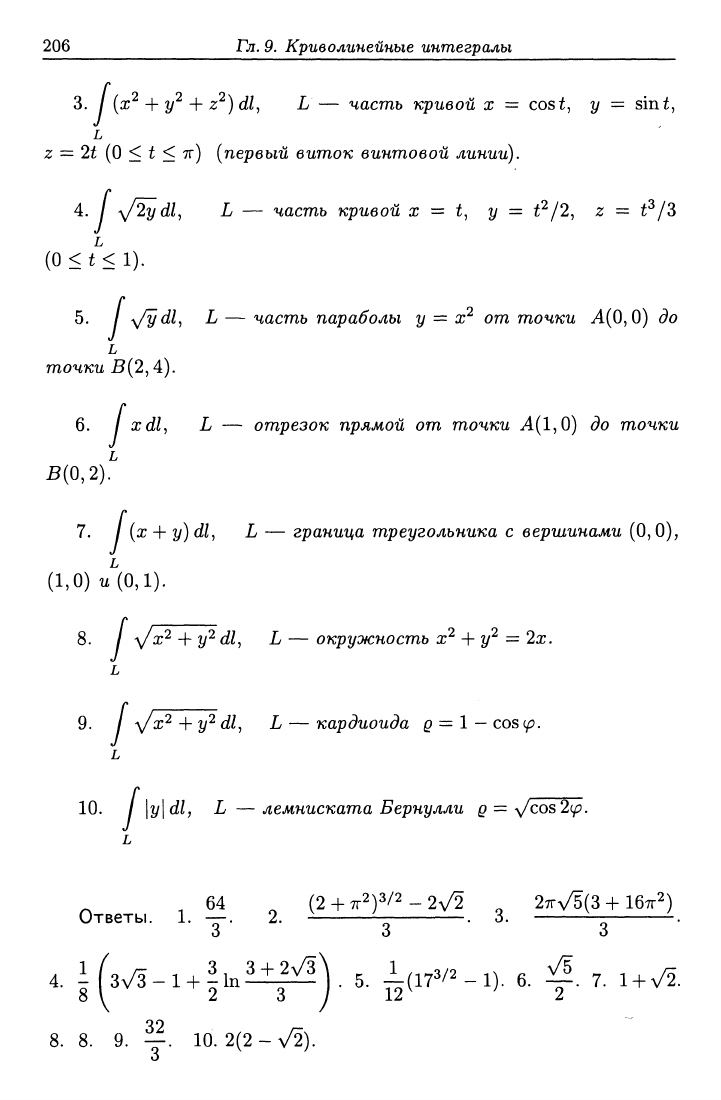
206 Гл.

Криволинейные интегралы

/ (ж^ + 2/^4- z^)

dl^

L — часть кривой х = cost, у = sint,

Z ~ 2t

{О

< t <

тт)

[первый виток винтовой линии).

A.j^ydl, L - паст, приео, . = t, у = f

12,

г = t^Z

{0<t< 1).

/ y/ydl^ L — часть параболы у — х^ от точки А(0,0) до

точки Б(2,4).

6. xdl, L — отрезок прямой от точки Л(1,0) до точки

B{Q,2Y

7. {х

-\-

у)

dl^

L — граница треугольника с вершинами (0,0),

(1,0)4о,1).

8. / л/хМ-^б?/, L — окруэюностъ х'^

-\-

у"^

= 2х.

10.

/ \у\ dl, L — лемниската Бернулли д = ^/cos2(p.

, 64 „ (2 + 7г2)3/2 _ 2\/2 , 27гч/5(3 + 1б7г2)

Ответы. 1. -. 2. ^ . 3. .

..^(3V3-i.ibilM).5.>--i).e.f.r.i.V2.

8. 8. 9. —. 10.2(2-72).

9.2. Криволинейные интегралы второго рода 207

9.2. Криволинейные интегралы

второго рода

ПОСТАНОВКА ЗАДАЧИ. Вычислить криволинейный интеграл

/ Р(ж,

2/,

z) dx + Q(x,

2/,

z) dy + R{x, y, z) dz

где L — часть гладкой кривой, заданной параметрически

= x{t),

у = y{t), ti<t< ^2,

z = z{t).

ПЛАН РЕШЕНИЯ. Криволинейный интеграл второго рода по кри-

вой L определяется формулой

/ Р(ж,

г/,

z) dx

-Ь

Q{x, у, z) dy + R{x, у, z) dz =

(1)

j[P{x{t)^),z{t))x\t)^-Q{x[t)^),z{t))y\t) +

Вычисляем

x'{t),

y'{t) и

z'[t).

Вычисляем криволинейный интеграл по формуле (1) и записы-

ваем ответ.

ЗАМЕЧАНИЕ 1. Если граничные точки кривой L M{xi,yi,zi) и

^{х2,2/2,

^2) заданы в декартовых координатах, то ti и

определяем,

решая системы уравнений

XI =x(ti), ( Х2 =x{t2),

2/1 =

y{ti),

I У2= 2/(^2),

Zl = Z{ti)] [

=z{t2).

ЗАМЕЧАНИЕ 2. Если кривая задана как линия пересечения двух

поверхностей:

Г Fi(a:,2/,z) = 0,

\ F2{x,y,z)=0,

то ее необходимо параметризовать.

208 Гл. 9. Криволинейные интегралы

ПРИМЕР

1. Вычислить криволинейный интеграл

/ - dx

—

Зх dy

-\- X

ПО

части кривой L, заданной параметрически

2 cos

y = 2smt, 0<t<~,

z = 1-2cost-2smt.

РЕШЕНИЕ.

Вычисляем: x'{t) =

—2sinf,

y'{t) = 2costH z\t) = 2sint-2cos 1

Вычисляем криволинейный интеграл по формуле (1):

—

Sxdy + xdz =

7г/2

= / ~ sint(-2sint) - 6cost(2cost) 4-2cost(2sint - 2cost) dt =

2//3 dx

—

3xdy + xdz = 2 —--тг.

ПРИМЕР

2. Вычислить криволинейный интеграл

I {х

—

y)dx-\- dy

-\-

zdz

от точки М(2,0,4) до точки 7V(—2,0,4) {у > 0) по кривой L, образо-

ванной пересечением параболоида z = x^ +у'^ и плоскости z = 4,

РЕШЕНИЕ. В сечении получается окружность

^2 4- 2/2 = 4,

2 = 4.

9.2. Криволинейные интегралы второго рода 209

Поэтому параметрические уравнения кривой L имеют вид

2 cos

у = 2sm t,

z = A.

Вычисляем: x\t) = -2sint, y'{t) = 2cost и z'{t) = 0.

Определяем ^i и ^2 из условий

2 = 2costi, ( —2 = 2cost2,

0 = 2sinti, I 0 = 2sint2,

4 = 4; [4 = 4.

Учитывая, что у > О, получаем ti =

и ^2 = тг.

Вычисляем криволинейный интеграл по формуле (1):

тг

I [х

—

y)dx-\- dy

-\-

zdz = / [(2cost - 2sint)(-2sint) + 2cost]c?t = 27г.

L 0

Ответ. / {x

—

y)dx-\- dy

-\-

zdz = 27Г.

Условия ЗАДАЧ. Вычислить криволинейные интегралы.

/(,^ - .^) .X + 2уг dy - .^ d., L - паст. .риеоП . = t,y = t^

Z = t^ от точки М{0,0,0) до точки N{1,1,1).

—

y)dx-\-xdy, L — арка циклоиды х = t

—

sint,

:l-cost (0<t<27r).

ydx + zdy-\-xdz, L — первый виток винтовой линии

•-

cost, у = sint, z

—

/(X 4- y)d. + (. - y)dy, L - оппжпосгп. (x - 1)^ + (, - 1)-4.

^ f (x

-{-

y)dx

—

y)dy _ 9 r>

/ -^^ :z :: , L — окруэюностъ x^

-\-

y^ = 1.

J x^ Л-у^