Зимина О.В., Кириллов А.И., Сальникова Т.А. Высшая математика. Решебник

Подождите немного. Документ загружается.

170 Гл.

Неопределенный

интеграл

ПЛАН РЕШЕНИЯ.

1. Чтобы избавиться

от

радикала, используем тригонометричес-

кие или гиперболические подстановки:

а)

X = asint или х = aiht]

б)

atgt или X = asht]

в)

х = или X = acht.

cost

Применив формулу замены переменной в неопределенном ин-

теграле, получим интегралы вида

Ri {sin t,

cos

t)dt.

Вычисляем последний интеграл с помощью известных подста-

новок или методом понижения степени.

Возвращаемся к переменной х и записываем ответ.

ПРИМЕР. Найти неопределенный интеграл

dx.

РЕШЕНИЕ.

Чтобы избавиться от радикала, воспользуемся подстановкой

ж = 3 sin t. Тогда dx =

cos t и \/9

—

x^ =

cos t.

Сделаем замену переменной в неопределенном интеграле:

Г х'^ ^ rdsiii^tScost ^^ л /* . 2.^.

/ . dx= —==== dt = 9

sm"^

t dt.

У V9-a;2 J V9-9sin2^ j

Применяя формулы понижения степени, получим

9 /* 9 9/* 9 9

sin^

tdt=-- / {l-cos2t)dt = -t-- / cos2t dt= -t--sm2t-i-C.

Возвращаемся к переменной x, подставляя t = arcsin(x/3):

..2

r.2

= - arcsm - - - sm

I 2

arcsm

•5-)

+ С

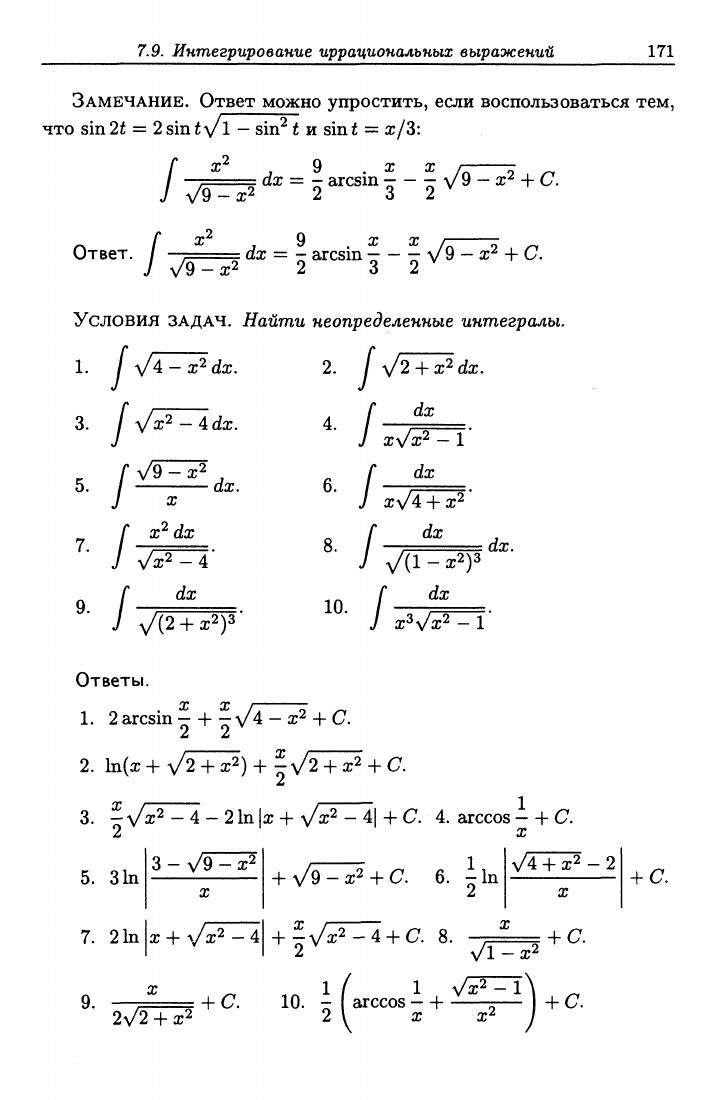
7.9. Интегрирование

иррациональных

выражений

171

ЗАМЕЧАНИЕ. Ответ можно упростить, если воспользоваться тем,

что sm2t = 2sintv 1 - sin^ t и sint = x/3:

/ ^'

dx = - axcsin - -

—

v 9

—

x'^

+ C.

Vg^T^ 2 3 2 "^

Ответ

•/

^ ^ ^ .XX /-—-

J ax = - arcsm

—

- -r v 9 - x^ + G.

v/9^:^

2 3 2 "^

Условия ЗАДАЧ. Найти неопределенные интегралы.

/* \/4 - х2 dx. 2. / \/2 + х2 dx.

/ V х^

— 4

dx.

х/(2 + х2)3

Ответы.

/ '^^ .

У х\/х2

—

6. /" /^

J XV 4 -f х^

8. / , dx.

f ^^

J WP^'

2arcsin - -f -\/4 - x2 + a

ln(x + V2 + x2) + -\/2 + x2 + C.

31n

x2-4-21n|

3 - \/9 - x2

x 4- л/х2

—

^ , r

2\/2

+ X2

-f \/x2 -

+ с 4. arccos —h С

- 1

+ \/9-x2 + a 6. ^in

+ ±,/^2_4 +

Г7.

8 i

\/4 + x2 - 2

L—+ Г7.

^ Vl-x2

10.

- arccos - + X— + C.

2 1 X x2 /

+ a

172 Гл.

Неопределенный

интеграл

7.10. Интегрирование

дифференциального бинома

ПОСТАНОВКА ЗАДАЧИ. Найти неопределенный интеграл

x'^{a

+ bx'')Pdx, (1)

где т, п и р — рациональные числа.

ПЛАН РЕШЕНИЯ. Выражение х^{а +

Ъх'^У

dx называется диффе-

ренциальным биномом. Условия его интегрируемости в элементар-

ных функциях получены П. Л. Чебышевым.

Условил Чебышева. Интеграл (1) выражается через конечную

комбинацию элементарных функций в следующих трех случаях:

1) р — целое число; в этом случае подстановка ж = z^, где s —

общий знаменатель дробей тип, приводит к интегралу от рацио-

нальной функции.

2) целое число; в этом случае подстановка а +

Ьх"^

= z^,

где S — знаменатель дроби р, приводит к интегралу от рациональной

функции.

. т-\-1 -г, 1

р — целое число; в этом случае подстановка ах " +

= 2^, где S — знаменатель дроби р, приводит к интегралу от рацио-

нальной функции.

ПРИМЕР. Найти неопределенный интеграл

Vx^

•

dx.

РЕШЕНИЕ. Перепишем интеграл в виде

J X

Ж^

Подынтегральное выражение имеет вид х'^{1 -h x^Y при

7 1 1 m+1

m=--, n=~, P=~, +p = -l.

5 3 5 n

Следовательно, имеет место третий случай интегрируемости.

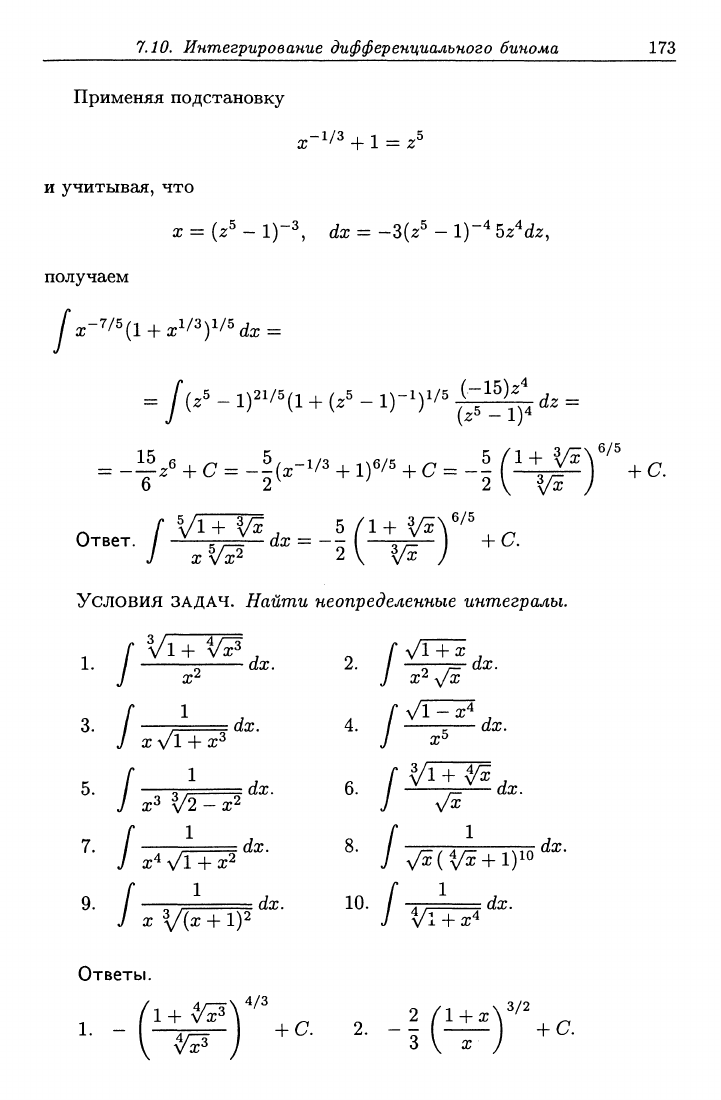
7.10. Интегрирование

дифференциального

бинома 173

Применяя подстановку

х-^1^

+ 1 = z^

и учитывал, что

x = {z^ ~ l)-^ dx = -3(г^ - 1)-'* bz^dz,

получаем

= /(/ - 1)""(1 + (.» - !)-')•"> i^

<i.

Условия ЗАДАЧ. Найти неопределенные интегралы.

__^_ dx, 4. / •

\/1 +

а;3

• ' J

/ dx. 4. / .'^ dx.

^- J xWl +

x^'^''-

^- /Т^^

9. / ^—= dx. 10. / д, dx.

V5+l)io'^'''

Ответы.

- Г иАГ I +а 2. -г(^^) 4-а

1Н-

V х-^ \ ^ ^ 2/1 + ж^'

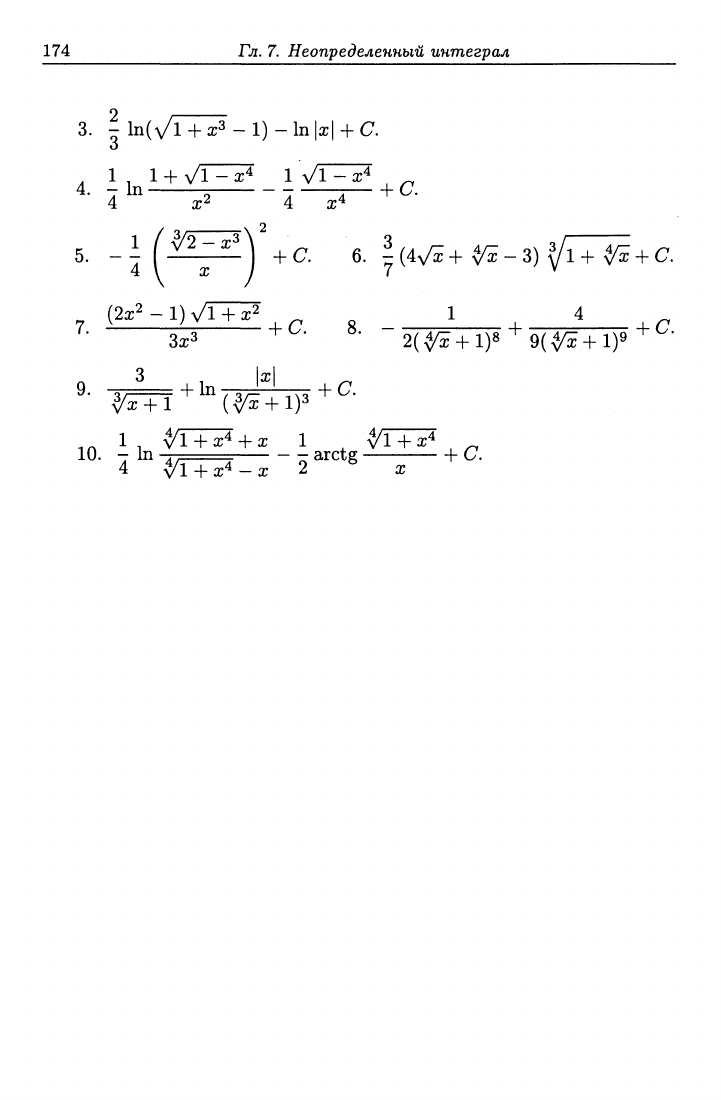
174 Гл.

Неопределенный

интеграл

- ln(vT+^-l)-ln|a;| + a

^ 1,1 + Vr^^ 1 VT^^ , ^

4 \ X

\ +С. 6. ^(4ч/г+-^-3)^1+-^ + а

(2х^-1)7ГГ^ 1,4

3x3 +^-- »• 2(^ + 1)8 ^9(^ + 1)9 ^^'•

3 |ж|

VaJ + l (^+1)3

1 ^/TTF+x 1 ^/TTF , ^

10.

- m ., arctg h С.

4 ^/ГТ^-а; 2 ^ a;

Глава 8

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

При изучении темы ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ вы познако-

митесь с формулой Ньютона-Лейбница и научитесь применять ее для

вычисления определенных интегралов, используя технику нахождения

первообразных. Вы научитесь применять определенные интегралы

для решения геометрических задач (вычисление площадей плоских

фигур, длин дуг кривых и объемов тел).

С помощью пакета РЕШЕБНИК.ВМ вы можете найти новые пре-

делы интегрирования (при использовании различных подстановок),

вычислить первообразные и применить формулу Ньютона-Лейбница,

выполнить все численные расчеты и проверить правильность полу-

ченных вами результатов.

8.1.

Интегрирование подведением

под знак дифференциала

ПОСТАНОВКА ЗАДАЧИ. Вычислить определенный интеграл

/ F{x)g{x) dx.

ПЛАН РЕШЕНИЯ. Пусть д{х) имеет очевидную первообразную

G(x),

а F{x) есть функция этой первообразной, т.е. F{x) = u{G{x)).

Тогда

6 6 (3

I F[x)g{x) dx= f u{G{x))G\x) dx = f u{G) dG,

a a a

где a = G(a), p = G{b).

Такого рода преобразование называется подведением под знак

дифференциала.

176 Гл.

Определенный

интеграл

Если метод избран удачно, то последний интеграл оказывается

табличным или известным образом сводится к табличному, после

чего применяем формулу Ньютона-Лейбница.

ПРИМЕР. ВЫЧИСЛИТЬ определенный интеграл

xdx

РЕШЕНИЕ.

Представим подынтегральное выражение в виде произведения

двух функций F{x)g{x), где д{х) имеет очевидную первообразную

G(x),

а F{x) есть функция этой первообразной, т.е. F{x) = u{G{x)).

В данном случае

П^)-^^^[^2)2^

^Н = 2х, G{x) = x\ F{x)

l^-^^u{G).

Тогда

11 1

Г xdx _1 f 1 2_1А 1

J ^^й^^2 J

(а:2)2 "^"^

^2 J TTG^"^^'

0 0 о

где G = ^2 и G(0) =

О,

G(l) = 1.

Последний интеграл является табличным. Применяем формулу

Ньютона-Лейбница:

^ г xdx 7Г

Ответ. / —т 7 = --.

J х^ + 1 8

Условия ЗАДАЧ. Вычислить определенные интегралы.

1 7г/4

ж , ^ f sin

а:

—

cos

а:

О о

X —

cos

а:

(cos

-Ь sinx)^

8.2. Интегрирование по частям 177

1 7г/4

У (а;4 + 4ж 4-2)2 J

о • ' Ь

\/2/2

/ ах. 6. / , ах.

X J vT^T^

1 о

7Г/2 1

/"ж

COS X

+ sin

, ^ /'2 arctg

а:

/ —7—: гз—ах. 8. / ——^ «^•

7г/4 о

г 9 яггстп т

-I-

•

dx.

4 1/2

3\/хН-1 , ^^ /*

arcsin

Н-X

fp^tLd..

10. / ^

У 2xv/i + x У х/ГГ^

1 о

Ответы.

1.1/4.

2.-1/4. 3.5/56. 4.1. 5.5/4. 6.7г/12. 7.14/7г2.

8. 7г2/16 + In

\/2.

9. 1п(20/3). 10. (тг^ - 18\/3 + 36)/36.

8.2. Интегрирование по частям

ПОСТАНОВКА ЗАДАЧИ. Вычислить определенный интеграл

/ F{x)g{x) dx.

ПЛАН РЕШЕНИЯ. Пусть на отрезке [а,

Ь]

функция ^(х) имеет оче-

видную первообразную G(x), а F{x) — дифференцируемая функция,

причем ее производная /(х) == F'{x) является более простой функ-

цией, чем F[x). Тогда применяем формулу интегрирования по час-

тям

ъ ь

I F{x)g{x) dx = F{x)G{x) \\- j f{x)G{x) dx.

a a

Если метод избран удачно, то интеграл в правой части этого ра-

венства оказывается табличным или известным образом сводится к

табличному, например повторным интегрированием по частям.

178 Гл.

Определенный

интеграл

ПРИМЕР. ВЫЧИСЛИТЬ определенный интеграл

х1п^

xdx.

РЕШЕНИЕ.

Представим подынтегральное выражение в виде произведения

двух функций F{x)g{x)^ где д{х) имеет очевидную первообразную

G(a:),

а F{x) — дифференцируемая функция, причем ее производная

f{x) = F'{x) является более простой функцией, чем F{x).

В данном случае

F{x)=ln'^x, д{х)=х, С(ж) = —, /(х) = F'(x) = 21пх •-.

Применяем формулу интегрирования по частям

2 о 2 2

х1п^

xdx = — In^

— / —

• 2

X • — б?ж

In^

—

dx.

1 У 2 X J

1 1 1

Последний интеграл не является табличным, но к нему можно

повторно применить формулу интегрирования по частям:

2 . .о 2

2 Г.2 , ^

/• х^ Г Гх^ 1

2 \^ J 2 X

= 21п2--7.

1 4

Ответ. / xln^xcia:^ 21n^2-21n2-f-.

I-

Условия ЗАДАЧ. Вычислить определенные интегралы.

1 1

fxe-''dx. 2. [ xdiTctgxdx.

о о

8.3. Интегрирование тригонометрических

выраоюений

179

2 27Г

/ Inxdx. 4. / x^cosxdx.

./....

.,/„....

1 о

е 7г/3

1п^жс/ж. 8. /

:r-dx.

J cos^

1 о

7г е '

9. e^cos^xdx. 10. / cos In

do:,

о 1

Ответы. 1. (е-2)/е. 2. (тг - 2)/4. 3.

21п2-1.

4. 47г. 5.7г/6-\/3+1.

6. 7г2/4 - 2. 7. е - 2. 8. 27г/3 - In tg(57r/12). 9. 3(е^ - 1)/5.

10.

(е^/2 - 1)/2.

8.3.

Интегрирование выражений

J?(sinx,cosx)

ПОСТАНОВКА ЗАДАЧИ. Вычислить определенный интеграл

/ i?(sina:,cosx) dx,

где R — рациональная функция двух переменных.

ПЛАН РЕШЕНИЯ.

Если а и b таковы, что функция tg {х/2) определена на [а,

6],

то

с помощью подстановки

интегралы от функций Я (sin

ж,

cos

ж)

приводятся к интегралам от ра-

циональных функций новой переменной t. Действительно, подставляя

в подынтегральное выражение