Зимина О.В., Кириллов А.И., Сальникова Т.А. Высшая математика. Решебник

Подождите немного. Документ загружается.

180 Гл.

Определенный

интеграл

получаем

/ 2t 1 —1'^\ 2

i?(sin

cos x)dx

—

R\ •- r, — ] dt

—

Ri (t) dt.

^ ^ \1 +

l + ^V 1 +

Подстановка t = tg(x/2) называется универсальной.

Находим новые пределы интегрирования

а _ Ь

« = tg-, i8 = tg-.

Применяем формулу замены переменной в определенном интег-

рале

г [21 1

—

t^\ 2

R{smx,cosx)dx =

J RyYTl^'TTt^j

ТТ^"^^'

a a

Вычисляем первообразную рациональной функции t и приме-

няем формулу Ньютона-Лейбница.

ЗАМЕЧАНИЕ. ЕСЛИ подынтегральная функция имеет специальный

вид, то лучше применить подстановки, требующие меньших вычис-

лений:

а) если- i?(sina;,cosx) = i?i(sina:,cos^ х) cosx, то применяем под-

становку t = sin

ж.

Действительно, подынтегральное выражение при-

обретает вид

Ri (sin

ж,

cos^ х)

cos

xdx = Ri

(t,

—t^) dt;

б) если R{sm x, cos x)

— R2

(sin

ж,

cos x) sin x, то применяем подста-

новку t ~ cos

Ж.

Действительно, подынтегральное выражение приоб-

ретает вид

Дз(sin^

cos х) sin xdx =

—R2 (1 —

t^, t) dt;

в) если i^(sinx,cosa:) = i^3(tgx), то применяем подстановку

t = tgx (при условии, что функция tgx определена на [а,

6]).

Дей-

ствительно, подынтегральное выражение приобретает вид

Rs{tgx)dx = R3{t)Y:^dt.

8.3. Интегрирование тригонометрических

выраэюений

181

ПРИМЕР 1. Вычислить определенный интеграл

7г/2

sinx

ах.

2 -h sin

РЕШЕНИЕ.

Поскольку функция tg (ж/2) определена на [0,7г/2], сделаем под-

становку

t = tg-.

Подставляя в подынтегральное выражение

2t , 2 ,

получим

«--

= -^±^^dt = ^. ^-L^^^dt.

2 + sina; „ , 2t 1 +

{f^ + t^ l){f^ + 1)

Находим новые пределы интегрирования

f(o)

t{l) =

Применяем формулу замены переменной в определенном интег-

рале

7г/2 1

г sin ж . _ f 2^ ,.

J 2 + sinx''''"~y (^2+^ + 1)(^2 + 1)^^-

о о

Вычисляем первообразную рациональной функции t и применя-

ем формулу Ньютона-Лейбница

2t , ^ Г 4 2t + l

—

2 arctg t

о v^"^*^-V3

7Г

27Г

О 2

Зл/3*

7Г/2

_ , sin ж , 7Г 27Г

Ответ. / : dx = •-

' I

2 + sina: 2 З^З'

182 Гл.

Определенный

интеграл

ПРИМЕР 2. Вычислить определенный интеграл

arccos(l/\/6)

3tg2x-l ,

—9

—

ах.

РЕШЕНИЕ.

Так как подынтегральная функция имеет вид R{tg х) и функция

tgx определена на [0,arccos(l/\/6)], сделаем подстановку tgx = t.

Подставляя в подынтегральное выражение

= t, ах =

1 + ^2'

получаем рациональную функцию t:

3tg2x-l , 3^2-1 1 ,

—о ах = —г — at.

tg2x + 5 t2-h5 1+^2

Находим новые пределы интегрирования:

tg(0) = 0, tg I arccos

—j=

j = У/Б.

Применяем формулу замены переменной в определенном интег-

рале:

arccos(l/\/6) л/5

J tg2a: + 5 J t^ +

l + t2

0 0

Вычисляем первообразную рациональной функции t и применя-

ем формулу Ньютона-Лейбница:

v/5

3^2-1 1 ,

dt = — arctgt

^2 + 5 1 +

^ 4 t

И—^arctg-

ч/5

V5 ^ ч/5

Ответ. /

^^C^^..

= -;=-arctg^/5.

= —^ - arctg VE.

о v5

arccos(l/\/6)

^2^

8.4. Интегрирование тригонометрических

выраоюений

183

Условия ЗАДАЧ. Вычислить определенные интегралы.

7г/2 7г/2

/ (]^х. 2. / dx.

J 5 -h 4 sin

а:

cos x J 3-f5sina:-f3 cos x

0 0

7Г/2 7Г/2

f cos^

, ^ /" cos

/ —5 аж. 4. / аж.

J sin''a:-h sin

J 3 + cosa:

7Г/6 n/3

7Г/2 7Г/2

/^-i ,dx. 6. /^dx.

У sina:(l+ cosx) J sin^a;

тг/З 7г/4

7. /i±^dx. 8. /

J sm 2x

4cos2x-2sin2x + sin2x

7Г/4 0

7Г/4 7Г/4

sin

cos

sin^

cos

X -\-9

cos^

0 0

dx.

9. / 7-dx. 10. / —о г-^2:.

J 5 + cos^

118 1 \/2 \/2 \/б

Ответы. 1. -. 2. - In-. 3. In2- -. 4. arctg-^ ^arctg—.

Ь.\

+ \ЫЪ. 6.1. 7.1(V^-l + lnV3). 8.1. 9.-i=arctgy|.

10.

In— + arctg-.

8.4. Интегрирование выражений

ПОСТАНОВКА ЗАДАЧИ. Вычислить определенный интеграл

/ sin^'^x cos^"'xdx,

где т и п — нат,уральные числа.

184 Гл.

Определенный

интеграл

ПЛАН РЕШЕНИЯ. Применяем формулы понижения степени

11 1

sin^ а; =-(1

—

cos2a;), cos^x =-(1 + cos2x), sin

cos

= -sin 2а;

A Zt £i

ДО тех пор, пока не придем к табличным интегралам или к интегра-

лам, которые известным образом сводятся к табличным.

ЗАМЕЧАНИЕ. Полезно иметь в виду, что

27Г 27Г

/ sin/cxdx = 0, /

COS

kxdx = 0 {к EN).

о о

ПРИМЕР. ВЫЧИСЛИТЬ определенный интеграл

27Г

/ sin^ Зх cos^ Зх dx.

РЕШЕНИЕ. Применяя формулы понижения степени, имеем

27Г 27Г

/ sin'* Зх

cos"*

Зх dx = 2~^ / (2 sin Зх cos

Зх)"*

dx =

о о

27Г 27Г

-4 / о^г,4^^ 1^ _ 0-6 / /

= 2"^ у sin^ бх dx = 2-^ [{1 - cos 12х)^ dx

о о

27Г 27Г 27Г

= 2~^ / с?х - 2~^ / cos 12х dx + 2"^ / cos^ 12х dx =

0 0 о

27Г

27Г 27Г

==:2-^7г + 2-^ f dx +

2r-'^

/^cos24xdx = 2-^7r + 2-^7r = ^.

27Г

Зтг

sin^ Зх

cos"*

Зх dx = —7.

8.5. Интегрирование

иррациональных выраоюений

185

Условия ЗАДАЧ. Вычислить определенные интегралы.

sin^

cos^

dx. 2. /

sin^ x cos^ x dx.

0 0

7Г

7Г/2

/ sin^ - cos^ - dx. 4. /

cos^

dx.

4 4 У

7г/2 7г/2

sin^

dx. 6. /

sin^ х cos^

dx.

о о

7г/2 7г/2

8. 1 sm^'^xdx.

/ sin^

cos^ х dx. 8. / si

о о

7г/2 7г/2

9. /cos-.... 10./si»-xcos-x.x.

Ответы. 1. 7Г. 2. 7г. 3. тг. 4. бтг. 5. бтг. 6. Зтг. 7. тг.

(2п-1)!!

7г (2т-1)!! тг (2гг-1)!! (2т-1)!! тг

(2п)!!

2* (2т)!! 2* (2n + 2m)!! 2'

8.5. Интегрирование выражений

щ^'^Ш'

ax+b а ax±b

cx-hd'

cx-\-d'

ПОСТАНОВКА ЗАДАЧИ. Вычислит^ъ определенный интеграл

где R — рациональная функция и

p,q^...

— нат,уральные числа.

186 Гл.

Определенный

интеграл

ПЛАН РЕШЕНИЯ. С помощью подстановки

ах -\-Ь

сх

-\-

<",

где п — общий знаменатель дробей 1/р,

1/д,...,

приходим к интегра-

лам от рациональных функций.

ПРИМЕР. ВЫЧИСЛИТЬ определенный интеграл

4V2

-х- VT+x

•

ах.

(VxT2 + 4:у/2-х){х + 2)2

РЕШЕНИЕ.

Чтобы сделать подстановку, приводящую к интегралу от ра-

циональной функции, нужно преобразовать подынтегральную функ-

цию так, чтобы она содержала корни любой степени, но из одного

и т о г о ж

выражения вида ^^ ^j

•

Поэтому преобразуем подынтег-

ральное выражение, выделяя

л , ;~ :

i^-

J'-'

Применяем подстановку = t :

2 -h ж

4 8^

Делая замену переменной в определенном интеграле, получаем

Jl^-i

f '^V2T^-^ ^^ /-4^-1(^^ + 1)7 Bl\

J ( [2^\, .„У 4f + l 16 1, (f2 + l)2J

dt.

^+^^/2Т^И^

2)^

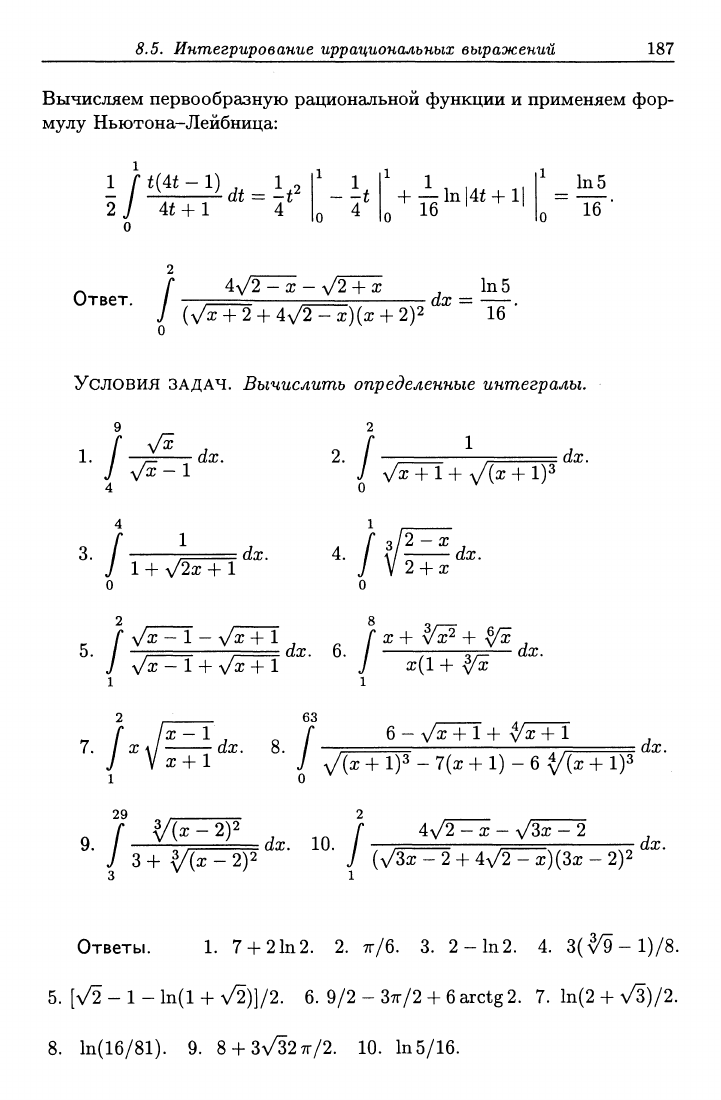
8.5. Интегрирование

иррациональных выраоюений

187

Вычисляем первообразную рациональной функции и применяем фор-

мулу Ньютона-Лейбница:

+ l 4

+ -lnl4t + l|

Тб"*

Ответ

•/

4V2 -

- V2 4-

_ In

Условия ЗАДАЧ. Вычислить определенные интегралы.

dx.

л/х

—

\/а;+ 1

ГУх-1

v^"=n:

/ , , da;. 6

. / \

J V^m+y/{x+l)^

dx.

f:(l+^

2 63

,|.^^. 8./-

б-ч/^ТТ+ \/5TT

V(x + 1)3 _ 7(^ + 1) _ 6 4/(x + l)3

У(^^^

з+У(х^^

dx. 10

4\/2 -

- V3x - 2

(V3x^^ + 4V2-i)(3x - 2)2

dx.

Ответы. 1. 7 4-2 In

2. тг/б. 3. 2-In

4. 3(v^-l)/8.

[\/2-l-ln(l

+ \/2)]/2. 6. 9/2-37r/2 + 6arctg2. 7. ln(2 + \/3)/2.

8. ln(16/81). 9. 8 + 3\/32

7г/2.

10. In5/16.

188 Гл.

Определенный

интеграл

8.6. Интегрирование выражений

R{x, (а^ ± х^/^) и R{x,

{х^

а^)!/^)

ПОСТАНОВКА ЗАДАЧИ. Вычислить определенные интегралы вида:

а) / R{xy \Jо?

—

ж^) dx\

б) f R{x,Va^ + x^)dx;

в) / R{x, v

ж^ —

а^) dx]

где R — рациональная функция.

ПЛАН РЕШЕНИЯ.

Чтобы избавиться от радикала, используем тригонометричес-

кие или гиперболические подстановки:

а) X = asint или х = atht]

б) X = atgt или X = asht;

в) х = или X = adit.

cost

Применив формулу замены переменной в определенном интег-

рале,

получим интегралы вида

/ Ri{sint^ COSt)dt или / Ri{sht, ch.t) dt.

ti tx

Вычисляем полученные интегралы с помощью известных под-

становок или методом понижения степени.

ПРИМЕР. ВЫЧИСЛИТЬ определенный интеграл

3/2

С х^

I . dx.

РЕШЕНИЕ.

Чтобы избавиться от радикала, используем подстановку

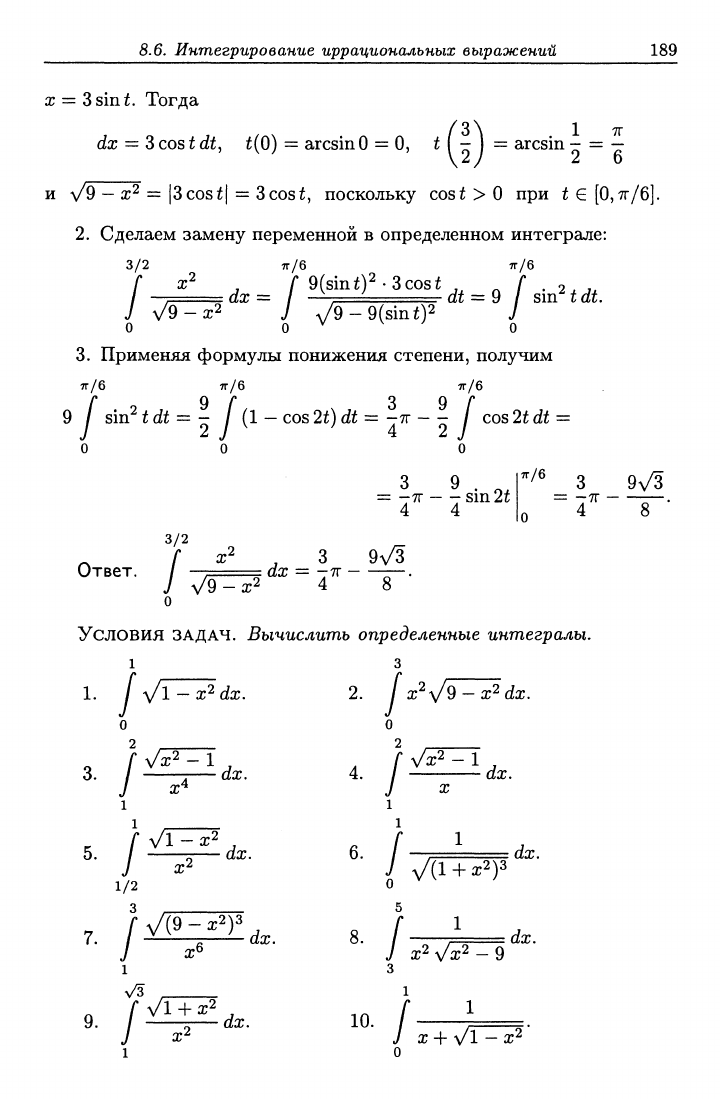
8.6. Интегрирование

иррациональных выраоюений

189

а: = 3sint. Тогда

dx = 3 cos t

dt^

t{0) = arcsin

= 0, м о I = arcsin - = 7-

V 2

/ 2 6

и y/9

—

x^= |3cost| = 3cost, поскольку cos^ > 0 при t G [0,7г/б].

Сделаем замену переменной в определенном интеграле:

3/2 7г/6 7г/6

/ х2 ^ /* 9(sint)2-3C0St ^^ п /" . 2.^.

/ , dx= \ ^ ==- dt = 9 sm^

d^.

л/9^^^

У л/9-9(8т^)2 У

о о ^ о

Применяя формулы понижения степени, получим

7г/6 7г/6 7г/6

9 / sin^ tdt = - / (1 - cos2t) dt = -тг - - / cos2tdt =

00 о

3 9 . ^ Г^^ 3 9\/3

= ~7Г Sin 2t = -7Г .

4 lo 4 8

3/2

Ответ. / , dx = -7г

—

'• /тг

4 8

Условия ЗАДАЧ. Вычислить определенные интегралы.

1 3

L. jy^T^^dx. 2. I

х'^у/\

1 1

1/2 о ^ ' '

3 , 5

у/(9-х2)з

da:.

J х^ J x^Vx^^

1 3

J x^ J x-hVl^

dx.