Зимин А.И., Сигаев Н.П., Сафонов Б.П. Сборник тестовых заданий и дидактических материалов по теоретической механике
Подождите немного. Документ загружается.

11
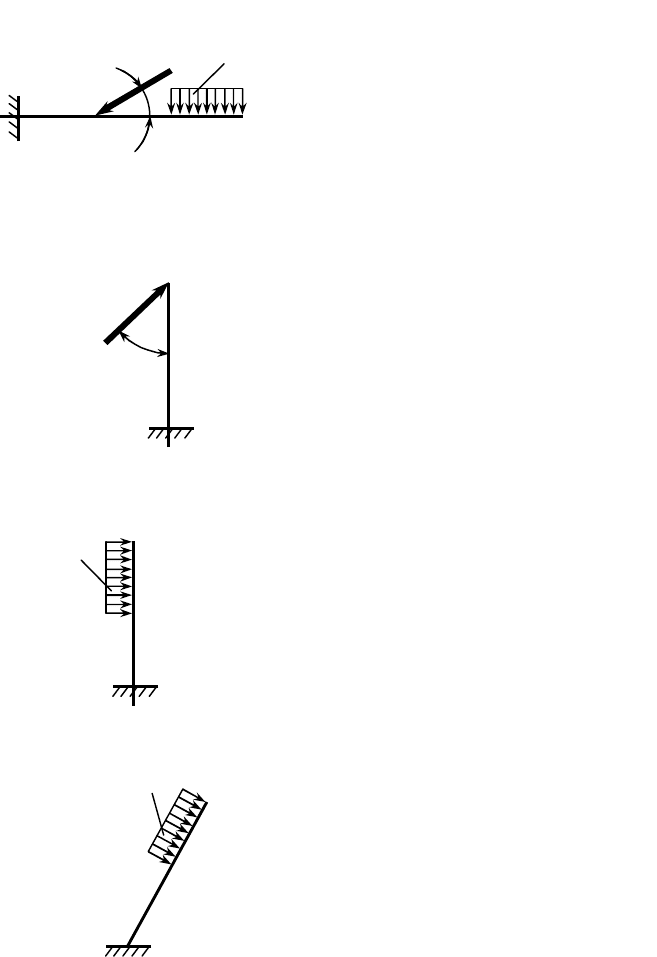
1.1.2.10.
1.1.2.11.
1.1.2.12.
1.1.2.13.
Определить величину силы
F
, при
которой момент в заделке
A
равен
мH
⋅
3700 , если интенсивность рас-
пределенной нагрузки мHq /200
=
;
размеры балки
мBCAB 2
=
=
,
мCD 3
=
. Определить также состав-
ляющие реакции заделки
A
X и
A
Y .
Определить силу
F
(в кН), при
которой момент в заделке
A
равен
мkH
⋅
56 , если расстояние
мAB 66,5
=
. Определить также
составляющие реакции заделки
A
X и
A
Y .
Определить интенсивность
q
распреде-
ленной нагрузки, при которой момент в за-
делке
A
равен мH
⋅
480 , если размеры
мAB 3
=
,
мAB 3
=
. Определить также
составляющие реакции заделки
A
X и
A
Y .
Определить длину участка
BC
, при которой момент в за-
делке
A
равен мH
⋅
180 , если
размер
мAC 2
=
и интенсив-
ность распределенной нагрузки
мHq /30
=
.
A
D
C
B
q
r
°
30
F
r
A
B
°
45
F
r
A
C
q
r
B
A
C
q
r
B
12
1.1.3. Равновесие системы двух тел под действием
произвольной плоской системы сил
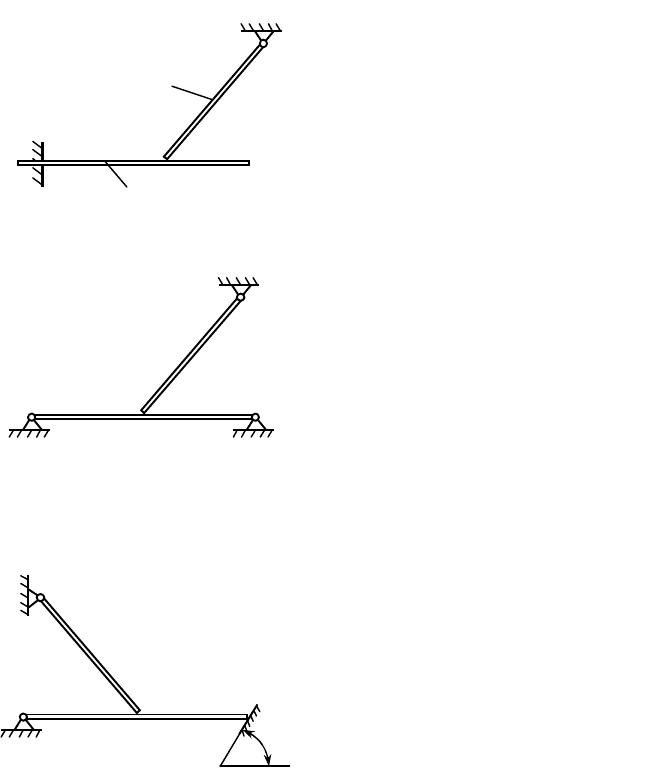
1.1.3.1.
1.1.3.2.
1.1.3.3.
Однородный брус 2 в
е
сом
H400 свободно опирается в точ-
ке
B
на однородную балку 1. Че-
му должен равняться вес балки 1,
для того чтобы момент в заделке
A
был равен мH
⋅
265 , если
размеры
мAB 1
=
, мBC 8,0
=
.
Однородная балка
AB
, вес
которой равен
кН
4
, в точке
B
свободно опирается на горизон-
тальный стержень
CD
. Опреде-
лить (в
кН
) реакцию подвижного
цилиндрического шарнира
D
, ес-
ли размеры
BDBC
=
. Весом
стержня
CD
пренебречь.
Однородная балка
AB
, вес ко
торой
H200
, свободно опирается в точке
B
на горизонтальную балку
CD
. Опре-
делить, с какой силой балка
CD
дей-
ствует на опорную плоскость в точке
D
, если расстояние
BDCB
=
, угол
°
=
60
α
. Весом балки
CD
пренеб-
речь.
A
B
C
2
1
A
B
C
D
B
A
B
C
D
°
60
13
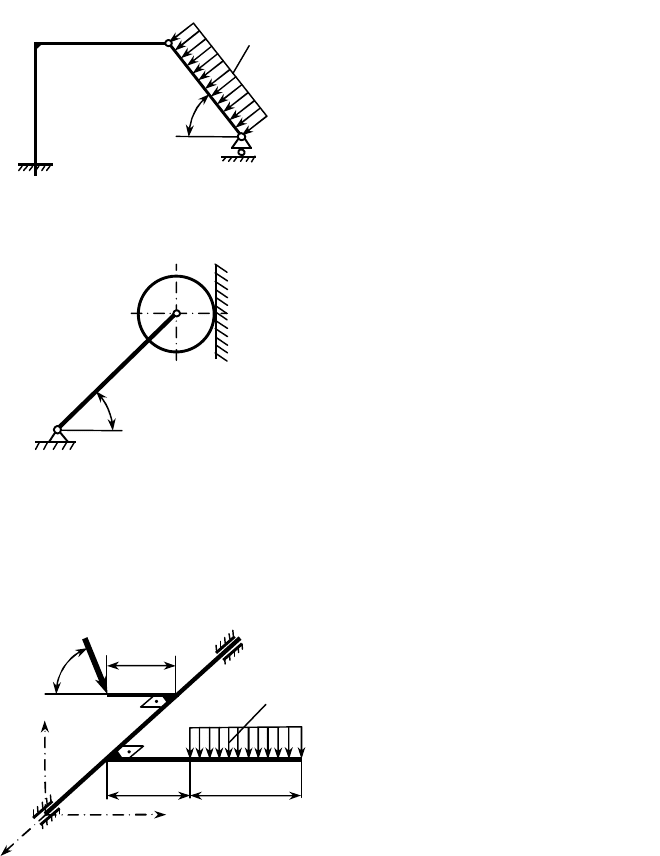
1.1.3.4.
1.1.3.5.
1.1.4. Равновесие тела под действием произвольной
пространственной системы сил
1.1.4.1.
Стержень
AB
, длина кото-
рого
м2
, нагружен равномерно
распределенной нагрузкой ин-
тенсивностью мHq /100
=
.
Определить реакцию опоры
A
.
На конце однородного стержня
AB
весом
H80
с помощью шарнира
B
установлен однородный диск весом
H200
. Диск опирается на вертикаль-
ную гладкую стену. Определить силу
воздействия диска на стену и состав-
ляющие реакции
A
X
и
A
Y опоры
A
.
B
A
q
r
°
45
B
A
°
45
К валу
OA
под прямым уг-
лом прикреплены стержни
BC
и
DE
. К стержню
DE
приложе-
на распределенная нагрузка
мHq /5,0
=
. Определить мо-
дуль силы
F
r
, уравновешиваю-
щей данную нагрузку, ес
ли
OxzF ||
r
.
x
y
z
O
A
q
r
E
C
D
F
r
°
60
м3
м4
м5
B

14
1.1.4.2.
1.1.4.3.
1.1.4.4.
Однородная квадратная
рама
OABC
со стороною
мa 5,0
=
и весом
HG 140
=
под действием наложенных
связей удерживается в горизон-
тальном положении. Опреде-
лить натяжение троса
BD
,
если угол
°
=
60
α
.
Cила HQF 1202
=
=
, при-
ложенная к шкиву, уравновешивает-
ся парой сил с моментом
мHM
⋅
=
18 . Определить состав-
ляющие реакции
A
X и
A
Y подшип-
ника
A
, если радиус шкива
мr 3,0
=
, расстояния мa 3,0
=
и
сила OyQF ||||
r
r
.
x
y
z
O
C
A
B
G
r
a3
α
a3
D
x
y
z
O
C
A
B
G
r
a
a
×
α
D
z
x
y
a
a
r
M
r
Q
r
F
r
Однородная плита
OABC
весом
HG 30
=
удерживается в горизонталь-
ном положении шарни
рами
AO, и тросом
BD
. Опре-
делить:
1) натяжение троса, ес
ли
мa 2
=
и угол
°
=
60
α
;
2) реакции шарниров
O
и
A
.

15
1.1.4.5.
1.1.5. Центр тяжести
1.1.5.1.
1.1.5.2.
Фигурная балка
OABD
находится в равновесии. Опре-
делить реакцию за
делки, если
дано: мOA 7,1
=
, ,2мAB
=
мBD 4,3
=
, OxBD ||
, сила
kHF 1
=
, интенсивность
распределен
ной нагрузки
мkHq
⋅
=
2
x
y
z
O
A
B
F
r
q
r
D
Определить коо
р-
динату
С
x центра тя-
жести площади круго-
вого сектора
OAB
,
если радиус мr 6,0
=
,
а угол
°
=
30
α
.
x
y
r
O
α
α
Определить координату центра
тяжести
C
y заштрихованной пло
щади
фигуры, если даны радиусы окружно-
стей: мR 99,0
=
, мr 33,0
=
.
x
y
O
R
r

16
1.1.5.3.
1.1.5.4.
Определить координату
C
z
центра тяже
сти однородного тела,
со
стоящего из конуса и цилиндра,
если высота мHH 4,02
1
== .
Определить координату
C
z
центра тяжести однородного тела,
состоящего из двух ци
линдров,
если высота ,2
1
HH =
радиус
,2rR
=
высота мH 5,0
=
.
x
y
z
O
H
1
H
x
y
z
O
H
1
H
r
R
17
1.2. Кинематика точки
1.2.1. Прямолинейное движение точки
1.2.1.1. Дано уравнение движения точки
tx
π
sin
=
. Определить
скорость в ближайший после начала движения момент времени
t
, когда ко-
ордината мx 5,0
=
. Определить ускорение точки в этот момент времени.
1.2.1.2. Точка движется по прямой с постоянным ускорением
2
/3,0 смa = . Определить начальную скорость точки, если через
6
секунд
после начала движения скорость точки стала равной
см /3
.
1.2.1.3. Точка движется по прямой с ускорением
2
/5,0 смa = .
Определить, за какое время будет пройдено расстояние
м9
, если при
0
0
=t скорость точки 0
0
=V . Какова будет скорость точки в этот момент
времени?
1.2.1.4. Сколько секунд должен работать двигатель, который сооб-
щает ракете ускорение g3 , чтобы скорость ракеты в прямолинейном дви-
жении возросла с
3
до
скм /5
?
1.2.1.5. Скорость автомобиля равна
часкм /90
. Определить тор-
мозной путь до полной остановки автомобиля, если среднее замедление его
при торможении равно
cм /3
.
1.2.2. Определение кинематических характеристик точки
при координатном и векторном способах задания движения
1.2.2.1. Заданы уравнения движения точки
tx 2
=
,
t
y
=
. Опреде-
лить время
t
, когда расстояние от точки до начала координат достигнет
м10
. Определить скорость точки в этот момент времени.
1.2.2.2. Заданы уравнения движения точки
tx 2
=
,
(
)
ty 1,0sin1−= . Определить ближайший момент времени, когда точка
пересечет ось
.Ox
Определить также скорость точки в этот момент времени.

18
1.2.2.3. Проекция вектора скорости точки на ось
x
(
)
tV
X
πcos2= .
Определить координату
1
x точки в момент времени ct 1
1
= , если при
0
0
=t координата .0
0
=x
1.2.2.4. Даны проекции вектора скорости точки на координатные
оси: tV
X
3= ,
2
2tV
Y
= ,
3
tV
Z
= . Определить модуль вектора ускорения в
момент времени ct 1
1
= с и его направление (направляющие косинусы). Рас-
стояния даны в метрах, время – в секундах.
1.2.2.5. Движение точки задано уравнениями
2
3,0 t
dt
dx
= и
3
2,0 ty = . Определить ускорение точки в момент времени
ct 7
=
и ско-
рость её в этот момент времени. Расстояния даны в метрах, время – в секундах.
1.2.2.6. Даны уравнения движения точки:
3
3,0 tx = ,
2
2ty = . Оп-
ределить, в какой момент времени
t
ускорение точки равно
2
/7 ссм . Опре-
делить также скорость точки в этот момент времени. Координаты
x
и
y
заданы в сантиметрах, время – в секундах.
1.2.2.7. Положение точки на плоскости определяется её радиус-
вектором jtitr
r
r
r
32
1,03,0 += . Определить модуль вектора ускорения точки
в момент времени ct 2
1
= с и его направление (по направляющим косину-
сам). Расстояния даны в метрах, время – в секундах.
1.2.2.8. Даны уравнения движения точки:
3
01,0 tx = ,
ty 10200
−
=
. Определить ускорение в момент времени, когда точка пере-
секает ось
Ox
. Как направлен вектор ускорения? Координаты
x
и
y
зада-
ны в метрах, время – в секундах.
1.2.3 Определение кинематических характеристик точки
при естественном способе задания движения
1.2.3.1. Точка движется по окружности согласно уравнению
.45,0
2
tts += Определить, в какой момент времени. Найти полное ускоре-
19
ние точки в момент времени, когда её скорость достигнет
см /10
. Радиус
окружности
мR 1
=
.
1.2.3.2. Касательное ускорение точки .2,0 ta =
τ
Определить мо-
мент времени
1
t , когда скорость
V
точки достигнет величины
cм /10
, если
при
0
t = 0 скорость смV /2
0
= . Какой путь пройдет точка за это время?
1.2.3.3. Проекции вектора скорости точки на оси координат опреде-
ляются выражениями:
2
2,0 tV
X
= , смV
Y
/3= . Определить касательное,
полное и нормальное ускорения точки в момент времени ct 5,2
1
= .
1.2.3.4. Точка движется по окружности согласно закону
2
4,05 tts −= . Определить момент времени
1
t , при котором нормальное
ускорение точки 0=
n
a , а также величину полного ускорения для этого
момента времени.
1.2.3.5. Дан закон движения точки по траектории:
ts 5
=
. Опреде-
лить радиус кривизны траектории в момент времени
1
t , при котором нор-
мальное ускорение точки смa
n
/3= , а также величину полного ускорения
точки в этот момент времени.
1.2.3.6. По окружности, радиус которой
мr 7
=
, движется точка со-
гласно закону
2
3,0 ts = . Определить момент времени
1
t , при котором нор-
мальное ускорение точки
2
/5,1 cмa
n
= , а также величину полного ускоре-
ния точки в этот момент времени.
1.2.3.7. Точка движется по окружности радиуса
мr 200
=
из со-
стояния покоя с постоянным касательным ускорением
2
/1 смa =
τ
. Опре-
делить полное ускорение точки в момент времени сt 20
1
= .
20
1.3. Кинематика твёрдого тела
1.3.1. Вращательное движение
1.3.1.1. При равномерном вращении маховик делает
4
оборота в се-
кунду. За сколько секунд маховик повернется на угол
π
ϕ
24
=
?
1.3.1.2. Ротор электродвигателя, начав вращаться равноускоренно,
сделал
100
оборотов за первые
5
секунд. Определить угловое ускорение
ротора и его угловую скорость через
10
секунд после начала вращения.
1.3.1.3. Тело вращается вокруг неподвижной оси согласно закону
2
3
+=tϕ . Определить угловую скорость тела в момент времени, когда
угол поворота рад10
=
ϕ
, а также его угловое ускорение.
1.3.1.4. Угловая скорость вращающегося тела изменяется согласно
закону
2
82 t−=ω . Определить промежуток времени от начала движения
до остановки тела, а также угол поворота тела за это время.
1.3.1.5. Угловое ускорение вращающегося тела изменяется согласно
закону
t2
=
ε
. Определить угловую скорость тела в момент времени
ct 4
1
= , если при 0
0
=t его угловая скорость равна нулю. Сколько оборо-
тов сделает тело за эти
4
секунды?
1.3.1.6. Тело вращается вокруг неподвижной оси согласно закону
3
24 t+=ϕ . Определить угловое ускорение тела в момент времени, когда
угловая скорость срад /6
=
ω
.
1.3.1.7.
1
d
2
M
Груз 1 поднимается с
помощью лебедки, барабан
2 которой вращается со-
гласно закону
3
25 t+=ϕ .
Определить скорость и ус-
корение точки
M
барабана
в момент времени ct 1
1
= ,
если ди
а
метр
м
d
6
,
0
=
.
