Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Нуриева С.Н., Дегтярева О.М. Математика в примерах и задачах
Подождите немного. Документ загружается.

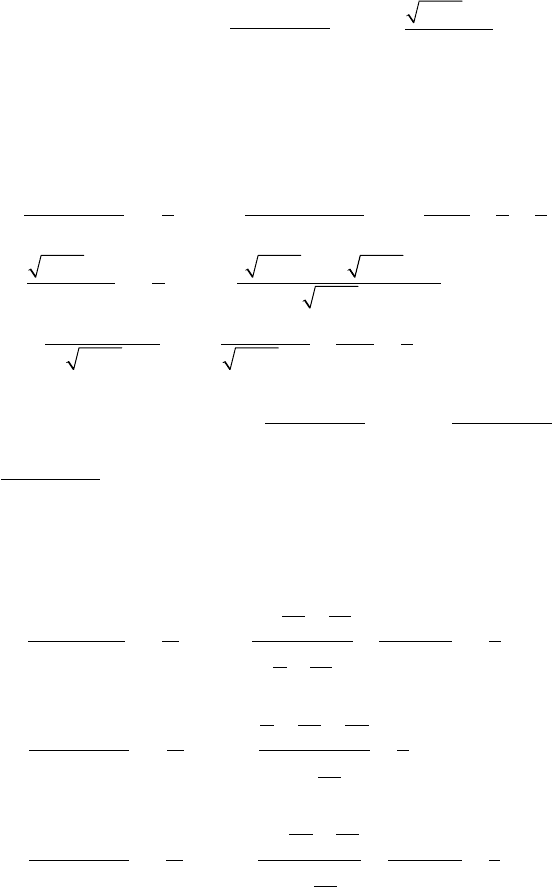
81
Задача 2. Вычислить: а)
lim;
x
x
xx
→
-
--
3
2
2
9
23
б)
lim.
x
x
x
→
+-
0
11
Решение: При подстановке предельного значения аргумента в
функцию в случаях а) и б) получаются неопределенности вида
{0/0}. Воспользуемся тем, что аргумент стремится к своему пре-
дельному значению, но не равен ему, и выполним тождественные
преобразования:
а)
limlim
()()
()()
lim
xxx
x
xx
xx
xx
→→
-
--
=
=
-+
+-
=
3
2
2
3
9
23
0
0
33
13
→→
+
+
==
3
3
1
6
4
3
2
x
x
;
б)
limlim
()()
()
lim
xx
x
x
x
xx
xx
→→
→
+-
=
=
+- ++
++
=
=
00
0
11 0
0
11 11
11
xx
xx x
x
+-
++
=
++
=
+
=
→
11
11
1
11
1
11
1
2
0
()
lim.
Задача 3. Вычислить: а)
lim;
x
xx
x
→∞
-+
-
3
2
23
5
б)
lim;
x
xx
xx
→∞
-+
+
3
4
23
2
в)
lim.
x
xx
x
→∞
-+
+
3
3
23
35
Решение: Имеем неопределенности вида {∞/∞}, которые можно
раскрыть, поделив числитель и знаменатель дробей на х
k
, где k —
старшая степень многочленов в числителе и знаменателе:
а)
limlim
xx
xx
x
xx
x
x
→∞ →∞
-+
-
=
∞
∞
=
-+
-
=
-+
-
=
3
2
23
3
23
5
1
23
15
100
00
11
0
=∞;
б)
limlim ;
xx
xx
xx
x
xx
x
→∞ →∞
-+
+
=
∞
∞
=
-+
+
==
3
4
34
3
23
2
12 3
1
2
0
1
0
в)
limlim
xx
xx
x
xx
x
→∞ →∞
-+
+
=
∞
∞
=
-+
+
=
-+
+
=
3
3
23
3
23
35
1
23
3
5
100
30
11
3
.
Переходя к общему случаю, получим правило:
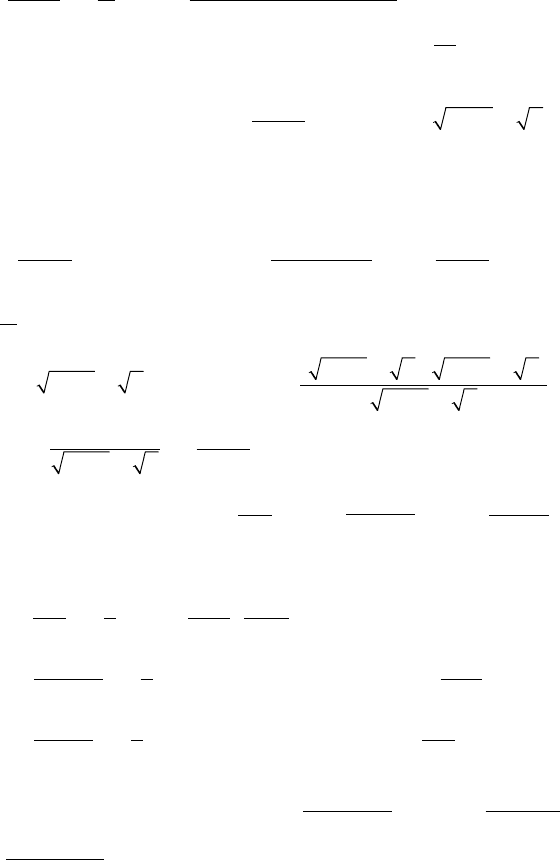
82
lim
()
()
lim
...
x
m
n
x
mm
m
n
Px
Qx
ax ax a
bx bx
→∞ →∞
-
=
∞
∞
=
+++
+
01
1
01
nn
n
b
mn
mn
a
b
mn
-
++
=
∞>
<
=
1
0
0
0
...
,,
,,
,.
Задача 4. Вычислить: а)
lim;
x
x
x
x
→∞
+
-
3
2
1
б)
lim( ).
x
xa x
→∞
+-
Решение: Имеем неопределенности вида {∞ - ∞}:
а) с помощью приведения к общему знаменателю переходим к
неопределенности вида {∞/∞}:
lim{}lim lim
xxx
x
x
x
xxx
x
x
x
→∞ →∞ →∞
+
-
=∞-∞ =
--
+
=
-
+
=
3
2
33
22
111
==
∞
∞
=
=
=
степень числителя
степень знаменателя
m
n
1
2
= 0;
б)
lim( ){ }lim
()()
()
lim
xx
x
xa x
xa xxax
xa x
xa
→∞ →∞
→∞
+- =∞-∞ =
+- ++
++
=
=
+
--
++
=
∞+∞
=
x
xa x
a
0.
Задача 5. Вычислить: а)
lim
tg
;
x
x
x
→0
б)
lim
arcsin
;
x
x
x
→0
в)
lim
arctg
.
x
x
x
→0
Решение: Имеем неопределенности вида {0/0}, которые раскры-
ваются сведением к I замечательному пределу (ОК, разд. 7.6):
а)
lim
tg
lim
sin
cos
;
xx
x
x
x
xx
→→
=
=⋅=⋅=
00
0
0
1
11 1
б)
lim
arcsin
arcsin ,
sin
lim
s
xy
x
x
xyy
xy
y
→→
=
=
=→
=
=
00
0
0
0
iin
;
y
= 1
в)
lim
arctg
arctg,
tg
lim
tg
xy
x
x
xyy
xy
y
y
→→
=
=
=→
=
==
00
0
0
0
11.
Задача 6. Вычислить: а)
lim
arcsin
;
x
x
xx
→
-
0
2
32
2
б)
lim
cos
sin
;
x
x
xx
→
-
0
1
3
в)
lim
tg sin
.
α
αα
α
→
-
0
3
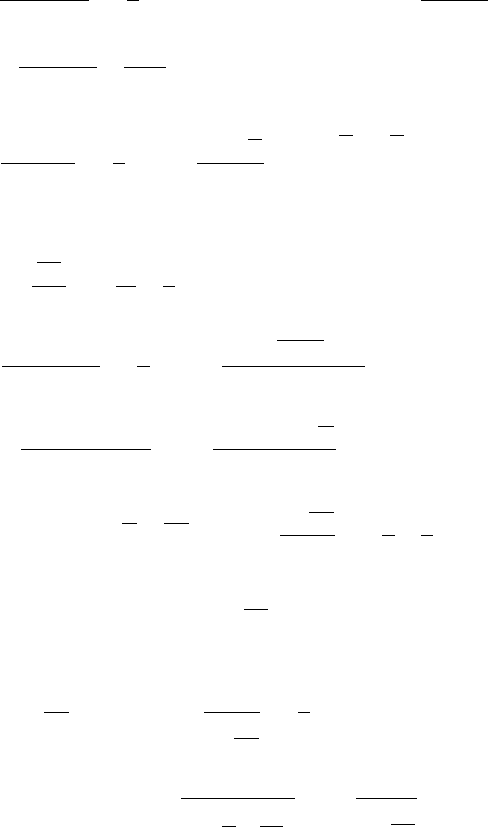
83
Решение: Имеем неопределенности вида {0/0}, которые легко
раскрыть, используя теорему об эквивалентных бесконечно малых
(б.м.) (разд. 7.7 ОК) и следующие б.м. (см. задачу 5): sin x ~ x,
tgx ~ x, arcsinx ~ x, arctgx ~ x при х → 0. Тогда:
а)
lim
arcsin arcsin (),
x
x
xx
xx
x
→
-
=
=
→
0
2
32
22
20
0
22
0
∼
=
-
=
=
-
=
-
=-
→
→
lim
lim
()
;
x
x
x
xx
x
xx
0
2
32
0
2
2
4
4
1
4
01
4
lim
arcsin arcsin (),
x
x
xx
xx
x
→
-
=
=
→
0
2
32
22
20
0
22
0
∼
=
-
=
=
-
=
-
=-
→
→
lim
lim
()
;
x
x
x
xx
x
xx
0
2
32
0
2
2
4
4
1
4
01
4
б)
lim
cos
sin
lim
sin
sin
sin
xx
x
xx
x
xx
xx
→→
-
=
==
00
2
2
1
3
0
0
2
2
3
22
∼
→
=
==⋅=
→
2
0
2
2
33
0
2
4
3
2
1
12
1
6
,
sin,
lim
xx
x
x
x
x
∼
;;
в)
lim
tg sin
lim
sin
cos
lim
αα
α
αα
α
α
α
α
→→
→
-
=
=
-
=
=
0
3
0
3
0
0
1
1
00
3
0
2
3
2
1
2
2
sin( cos)
cos
lim
sinsin
cos
sin,sin
αα
αα
α
α
αα
αα
α
-
=
⋅
=
=
→
∼
ααα
α
α
α
α
α
24
0
2
4
1
2
4
1
2
2
0
2
3
∼ ,
,
lim.
→
=
⋅
⋅= =
→
Задача 7. Вычислить
lim( )tg.
x
x
x
→
-
1
1
2
π
Решение: Имеем неопределенность {0 ⋅ ∞}, преобразуем ее к
виду {0/0} и сделаем замену переменных х - 1 = у, у → 0:
lim( )tg{}lim
ctg
,
xx
x
xx
x
xy
x
→→
-=⋅∞ =
-
=
=
=
-=
=
11
1
2
0
1
2
0
0
1
1
π
π
++→
=
-
+
=
-
-
=
=
→→
yy
y
y
y
y
y
yy
,
lim
ctg
lim
tg
tg
0
22
2
00
ππ
π
π
222
0
2
2
0
∼
π
π
π
y
y
y
y
y
,
lim.
→
==
→
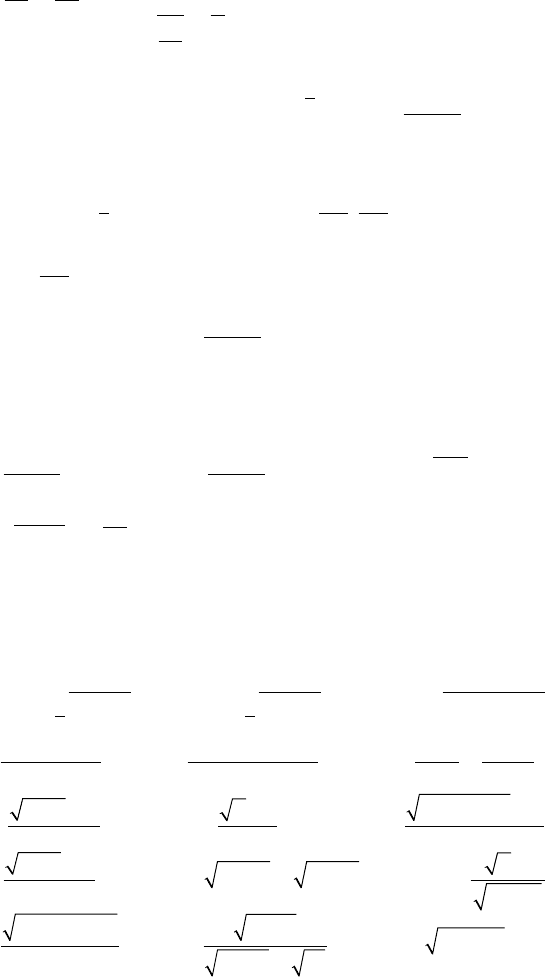
84
lim( )tg{}lim
ctg
,
xx
x
xx
x
xy
x
→→
-=⋅∞ =
-
=
=
=
-=
=
11
1
2
0
1
2
0
0
1
1
π
π
++→
=
-
+
=
-
-
=
=
→→
yy
y
y
y
y
y
yy
,
lim
ctg
lim
tg
tg
0
22
2
00
ππ
π
π
222
0
2
2
0
∼
π
π
π
y
y
y
y
y
,
lim.
→
==
→
Задача 8. Вычислить: а)
lim( sin);
x
x
x
→
+
0
1
1
б)
lim.
x
x
x
x
→∞
+
+
+
23
29
31
Решение: Имеем неопределенности вида {1
∞
}, которые раскры-
ваем, используя II замечательный предел (ОК, разд. 7.6):
а)
lim( sin) {} lim((sin ))
sin
sin
lim
s
x
x
x
x
x
x
xx
x
→
∞
→
+==+ =
=
→
0
1
0
1
111
0
e
iin
;
x
x
==ee
1
б) при вычислении
lim{}
x
x
x
x
→∞
+
∞
+
+
=
23
29
1
31
воспользуемся из-
вестной формулой
lim().
()
lim()( () )
xa
vx
vx ux
ux
xa
→
-
=
→
e
1
Имеем
limlim
lim(
x
x
x
x
x
xx
x
→∞
+
→∞
+
+
+
=-
+
=
→∞
23
29
1
6
29
31 31
3
e
xx
x
x
x
x
+-
+
--
+
-
-
=
===
→∞
1
6
29
18 6
29
18
2
9
)
lim
.eee
Задачи для самостоятельного решения
Вычислить следующие пределы:
5) а)
lim
sin
tg
;
x
x
x
→
+
π
4
1
б)
lim
sin
tg
;
x
x
x
→
-
π
4
1
6)
lim;
x
xx
xx
→
-
-+
2
2
2
2
44
7)
lim;
x
xx
x
→-
++
+
2
2
3
68
8
8)
lim;
x
xx
xxx
→
+-
--+
1
2
32
2
1
9)
lim;
x
x
x
→
-
-
-
1
3
1
1
3
1
10)
lim;
x
x
x
→
--
-
5
12
5
11)
lim;
x
x
x
→
-
-
1
4
1
1
12)
lim;
x
xx
x
→-
++ -
+
1
2
42
1
13)
lim;
x
x
x
→
--
-
9
3
12
9
14)
lim( );
x
xx
→∞
+- -
22
11
15)
lim;
x
xx
x
→∞
+
+
5
3
2
16)
lim;
n
nn
n
→∞
+-
+
231
2
2
17)
lim;
n
n
nn
→∞
+
++
4
5
5
4
3
1
3
18)
lim( );
x
xxx
→+∞
+-
2
4
85
19)
lim;
x
x
x
x
→∞
+
-
4
3
1
20)
lim
tg
sinsin
;
x
x
xx
→
⋅
0
2
2
35
21)
lim
cos
sin
;
x
x
xx
→
-
⋅
0
3
1
2
22)
lim
sin
;
x
x
x
→
+-
0
3
22
23)
lim
coscos
;
x
xx
x
→
-
0
2
αβ
24)
lim
cos
sin
;
x
x
x
→
-+
0
2
21
25)
lim
sin
sin
;
x
x
x
→π
3
2
26)
limtg;
x
xx
→
-
π
π
2
2
27)
lim
sin
;
x
x
x
→
-
-
π
π
2
2
1
2
28)
lim
sintg
;
x
xx
→
-
0
11
29)
lim( );
tg
x
xx
x
→
+
0
2
1
1
30)
lim;
n
n
n
n
→∞
-
+
1
5
2
1
31)
lim;
x
x
x
→∞
-
-
+
1
3
21
32
32)
lim;
x
x
x
x
→∞
+
-
+
34
32
1
3
33)
lim;
x
x
xx
xx
→∞
++
-+
2
2
54
37
34)
lim( tg );
x
x
x
→∞
+1
2
1
2
35)
lim(ln()ln ).
x
xx x
→+∞
+-1
Сравнить следующие бесконечно малые, пользуясь ОК
разд. 7.7:
36) α(x) = sin5x, β(x) = x + x
3
, x → 0; 37)
α() ,xx=+-611
β(x) = 3x, x → 0; 38)
α() ,x
x
x
=
-
+
1
1
β() ,xx=-1
x → 1;
39)
α() ,n
n
=
+
1
3
2
β() ,n
n
=
+
1
5
n → ∞; 40)
α() ,n
n
=
+
1
3
2
β() ,n
n
=
+
1
5
n → ∞; 41) α(x) = 3x sin x, β(x) = tg x, x → 0;
42) α(x) = x
2
- 2x - 3,
β()
()
,x
x
x
=
- 3
2
2
x → 3.
43) Первоначальный вклад в банк Q
0
денежных единиц. Банк
выплачивает ежедневно р% годовых. Найти размер вклада через
t лет при непрерывном начислении процентов.
Указание: Найти размер вклада Q
n
через t лет при начислении
процентов по вкладу n раз в году и перейти к пределу при n → ∞.
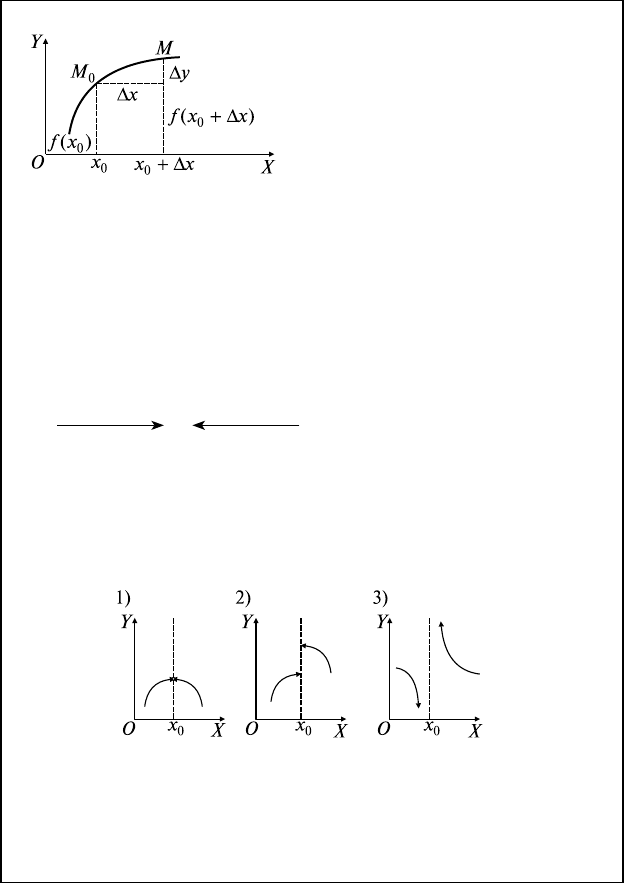
86
8. неПрерывные Функции одной Переменной
опорный конспект № 8
8.1. Определения непрерывности
∆y = f(x
0
+ ∆x) - f(x
0
) — прираще-
ние f(x) в точке х
0
О.1: f(x) непрерывна в т. x
0
⇔
1) f (x) определена в т. x
0
и ее
окрестности;
2)
lim
∆
∆
x
y
→
=
0
0
О.2: В О.1 вместо 2)
условие 2′)
lim()()
xx
fx fx
→
=
0
0
О.1 ~ О.2
(x
0
+ ∆x = x)
8.2. Точки разрыва (т.р.) — точки, в которых нарушается опреде-
ление непрерывности
lim()( )
xx
fx fx
→-
=-
0
0
0
0
— lim слева, x < x
0
;
lim()( )
xx
fx fx
→+
=+
0
0
0
0
— lim справа, x > x
0
:
x < x
0
x
0
x > x
0
Классификация т.р.:
1) устранимая т.р.: f(x
0
+ 0) = f(x
0
- 0), но f(x
0
)∃/;
2) т.р. 1-го рода: f(x
0
+ 0) ≠ f(x
0
- 0);
3) т.р. 2-го рода — остальные т.р.
8.3. Свойства функций, непрерывных в т. x
0
1
0
. ϕ(х), ψ(х) — непрерывны в т. х
0
87
⇒
+
⋅
≠
ϕψ
ϕψ
ϕψψ
() (),
() (),
() (),().
xx
xx
xxx 0
—непрерывны в т. x
0
.
2
0
.
y = ϕ(z) непрерывна в т. z
0
, z = ψ(x) непрерывна в т. x
0
,
z
0
= ψ(x
0
) ⇒ ϕ[ψ(x)] непрерывна в т. x
0
С л е д с т в и е: Элементарные функции непрерывны в областях
определения.
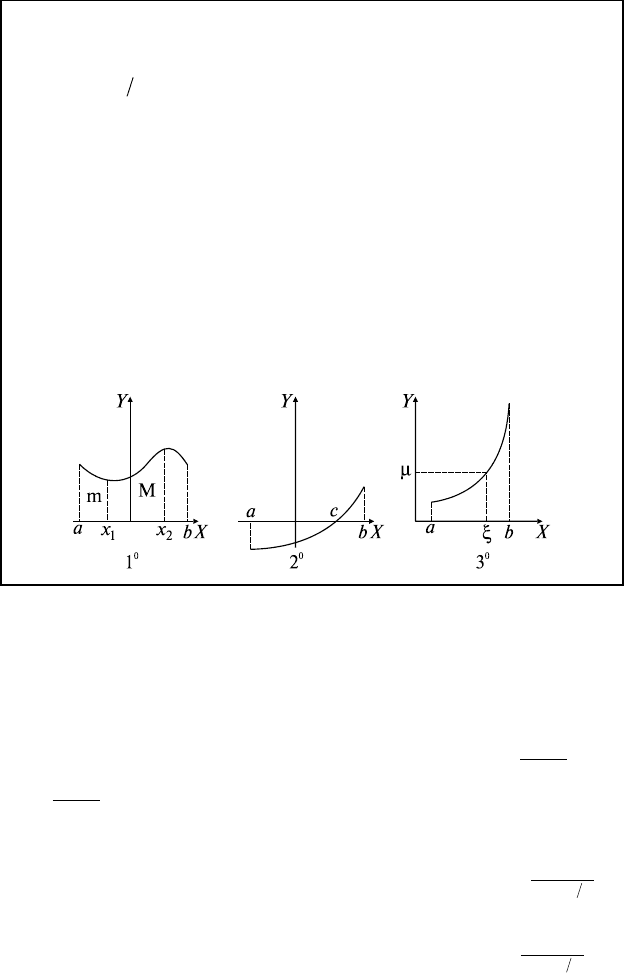
8.4. Свойства функций, непрерывных на [a, b]
(множество C
[a,b]
)
m — наименьшее, М — наибольшее значения f(x) на [a, b] ⇔
⇔ m ≤ f(x) ≤ M
1
0
. f(x) ∈ C
[a,b]
⇒ ∃x
1
, x
2
∈ [a, b]: f(x
1
) = m, f(x
2
) = M.
2
0
. f(x) ∈ C
[a,b]
, f(a) ⋅ f(b) < 0 ⇒ ∃c ∈ [a, b]: f(c) = 0.
3
0
. f(x) ∈ C
[a, b]
⇒ ∀µ между f(a) и f(b) ∃ξ ∈ [a, b]: f(ξ) = µ
Задачи к разд. 8
Задача 1. Показать, что при х = 4 функция у = х/(х - 4) имеет
разрыв.
Решение: Функция у = х/(х - 4) — элементарная, определенная
для х ∈ (-∞; 4) ∪ (4; ∞), в точке х = 4 она неопределена. Найдем
пределы функции в точке х = 4 слева и справа:
lim,
x
x
x
→+
-
=+∞
40
4
lim,
x
x
x
→-
-
=-∞
40
4
т.е. точка х = 4 — точка разрыва 2-го рода.
График функции показан на рис. 8.1.
Задача 2. Определить точку разрыва функции
fx
x
() .=
+
1
12
1
Решение: Точка, подозреваемая на разрыв, — это точка х = 0,
в которой функция неопределена. Тогда
lim,
x
x
→+
+
=
0
1
1
12
0
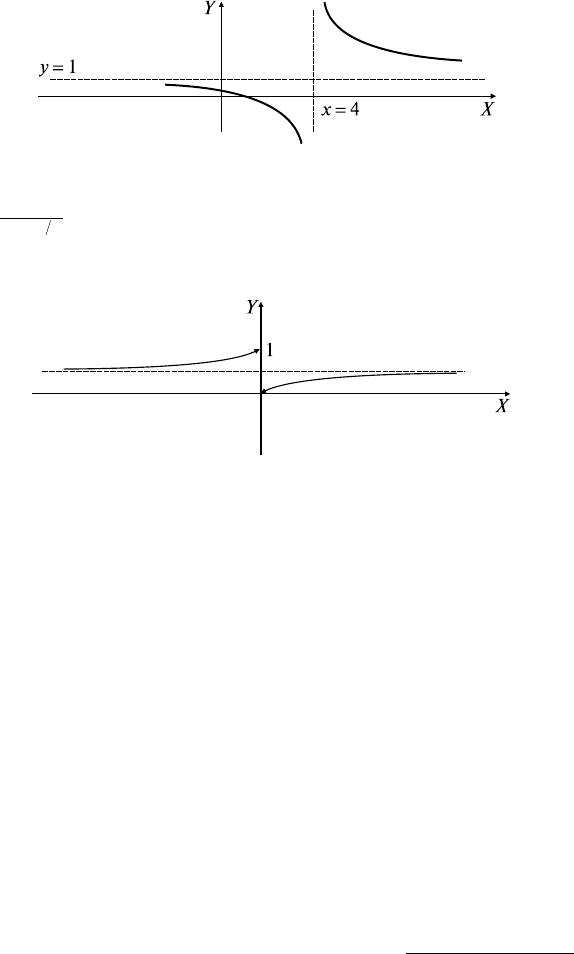
88
lim,
x
x
→-
+
=
0
1
1
12
1
т.е. в точке х = 0 — разрыв 1-го рода и функция
имеет скачок, равный 1 (рис. 8.2).
Задача 3. Найти точку разрыва функции
fx
xx
x
()
,,
,.
=
≠
=
2
2
12
Решение: Задана составная функция, определенная при
х ∈ (-∞, +∞). На разрыв подозреваем точку х = 2:
lim(),
x
fx
→-
=
20
4
lim(),
x
fx
→+
=
20
4
но f(2) = 1. Таким образом, точка х = 2 — точка
устранимого разрыва.
Задача 4. Исследовать на разрыв функцию
gx
xx
x
()
,,
,.
=
≠
=
2
2
42
Решение: Здесь g(2 - 0) = g(2 + 0) = g(2) = 4 ⇒ g(x) — непре-
рывна в точке х = 2 ⇒ точек разрыва нет.
Задачи для самостоятельного решения
Определить точки разрыва функций:
1) f(x) = x/|x|; 2) f(x) = arctg(1/x); 3)
fx
x
xxx
()
()()()
;=
+++
3
123
Рис. 8.2
Рис. 8.1

89
4)
fx
x
() ;
()
=
-
3
13
5) f(x) = lg(x
2
+ 3x).
варианты контрольной работы
Вариант № 1
1.
lim.
x
xx
xx
→
-+
-+
5
2
2
2115
710
Ответ: 3. 2.
lim
sin
.
x
x
x
→0
3
3
2
5
Ответ: 8/5.
3.
lim.
x
x
x
x
→∞
-
3
2
Ответ: e
-3/2
. 4.
lim.
x
x
xx
→∞
-
+-
34
231
5
73
Ответ: 0.
5.
limsin ctg.
x
xx
→
⋅
0
2
Ответ: 2.
Вариант № 2
1.
lim.
x
xx
xx
→
-+
-+
1
2
2
2
231
441
Ответ: ∞. 2.
lim.
x
xx
xx
→∞
++
-+
335
8710
3
3
Ответ: 3/8.
3.
lim
cos
tg
.
x
x
xx
→
-
0
71
24
Ответ: -49/16. 4.
lim( ).
x
x
x
→
+
0
5
110
Ответ: e
50
.
5.
lim( ).
x
xx
→∞
+- +
2
3
2
3
12 5
Ответ: ∞.
Вариант № 3
1.
lim.
x
x
x
→
+-
-
4
12 3
2
Ответ: 4/3. 2.
lim.
x
nnn
n
→∞
++
+
32
3
2
1
Ответ: 0.
3.
lim
arcsin()
.
x
x
xx
→-
+
+
2
2
2
2
Ответ: -1/2. 4.
lim( ).
x
x
x
→
-
-
3
2
3
38
Ответ: e
6
.
5.
lim.
x
x
x
x
x
→∞
-
-
+
3
2
2
21
21
Ответ: 1/4.
ответы к разд. 6, 7, 8
6.1. Элементы теории множеств
1) А ∪ B = {1, 2, 3, 4}, A ∩ B = {2, 3}, A\B = {1}; 2) a).
6.2. Функции
6.3. Основные элементарные функции. Элементарные функции
3) D( f ) = (-∞, ∞); 4) D( f ) = (-∞, 1) ∪ (1, 2) ∪ (2, +∞);
5) D( f ) = (-∞, -3) ∪ (2, +∞); 6) D( f ) = [-1/3; 1/4];
7) D( f ) = 1; 8) D( f ) = (2kπ, (2k + 1)π), k ∈ Z ;

9) E( f ) = (-∞, 3]; 10) E( f ) = (0, 1]; 11) [-2, 4]; 12) T = π;
13) T = 6π; 14) T = π; 15) Нечетная; 16) Четная; 17) Нечетная;
18) Четная; 19)
yx= sin;
2
20)
yx=+1
2
lg sin;
21) а) y = sinz,
z = cost,
tx= ;
б) y = lgz, z = tgt, t = 2
x
; в) y = arcsinz, z = e
t
,
tx=
3
;
22) а) f(ϕ(π/2)) = 0; б) ϕ( f(1)) = 0; в) f(ϕ(x)) = sin
3
2x -
- sin2x; г) f( f(x)) = (x
3
- x)
3
- x
3
+ x; д) ϕ( f(x)) = sin2(x
3
- x).
7.3–7.7. Бесконечно малые (б.м.) и бесконечно большие
функции. Леммы о б.м. Теоремы о пределах. неопределенности.
Cравнение б.м.
5) а)
2
/4; б) ∞; 6) ∞; 7) 1/6; 8) ∞; 9) -1; 10) 1/4; 11) 1/4;
12)
-
1
4
;
13)
1
12
;
14) 0; 15) ∞; 16)
2;
17) 0; 18) 2; 19) 0; 20) 4/15;
21)
3
4
;
22)
62;
23) (β
2
- α
2
)/2; 24)
2
/8; 25) -3/2; 26) 1; 27) 1/2;
28) 0; 29) е; 30) е
5
; 31) е
-9/2
; 32) е
-2/3
; 33) е
8
; 34) е
1/2
; 35) 1; 36) Од-
ного порядка; 37) α ~ β; 38) α ~ β; 39) α = o(β); 40) α ~ β;
41) α = o(β); 42) β = o(α); 43)
QQ
p
n
n
nt
=+
0
1
100
,
QQ
pt
=
0
100
e .
8. непрерывные функции одной переменной
1) х = 0 — разрыв 1-го рода, скачок равен 2; 2) х = 0 — разрыв
1-го рода, скачок равен π; 3) х = -1, х = -2, х = -3 — разрыв 2-го
рода; 4) х = 3 — разрыв 2-го рода; 5) х = 0, х = -3 — разрыв 2-го
рода.
