Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Нуриева С.Н., Дегтярева О.М. Математика в примерах и задачах
Подождите немного. Документ загружается.


71
Требуется:
а) написать уравнение прямой М
1
М
2
; б) найти угол ϕ между
прямыми М
1
М
2
и L; в) найти точку пересечения Q прямых М
1
М
2
и L; г) проверить на чертеже результат пункта в).
3. Даны четыре точки: М
0
(µ + 1; 1 - λ; ν + 1); М
1
(µ; -λ; ν + 1);
М
2
(2µ; -2λ; ν + 2); М
3
(µ + 1; 1 - λ; ν).
Требуется:
а) написать уравнение плоскости G, проходящей через точки
М
1
, М
2
, М
3
; б) найти расстояние d от точки М
0
до плоскости G;
в) написать уравнение плоскости G
1
, проходящей через точку М
0
и
параллельной плоскости G.
4. Даны плоскость G: (λ + 1)х + (1 - µ)y + z = ν(λ + 1) и прямая L:
λµ λν
µλν
xyz
xyz
-+=
++=++
,
.
Требуется:
а) найти направляющий вектор прямой; б) найти угол θ между
прямой и плоскостью; в) написать канонические и параметриче-
ские уравнения прямой; г) найти точку пересечения Q прямой и
плоскости, используя параметрические уравнения прямой.
5. Привести уравнения к каноническому виду и построить кри-
вые:
а) (µ + 1)х
2
+ (λ + 6)у
2
- 2(λµ + λ)х + 2(λµ + 6µ)у +
+ λµ(λ + µ - 6) + λ(λ - 6) + 6µ(µ - 6) - 36 = 0;
б) (λ + 1)х
2
- (µ + 1)у
2
- 2(λµ + µ)х + 2(λµ + λ)у +
+ λµ(-λ + µ - 4) + λ(λ + 4) + µ(µ - 4) - 4 = 0;
в) у
2
+ (µ + 1)х + 2λу + λ
2
- µ
2
- 3µ - 2 = 0;
г) х
2
- 2µх - (λ + 1)у - λ
2
+ µ
2
- 3 - 4λ = 0.
ответы к разд. 3, 4, 5
3.1.Прямая на плоскости
2) А ∈ L, B ∉ L; 3) arctg(8/9); arctg(4/3); arctg12; S = 12 кв. ед.;
4) М(-12; 5); 5) 77х - 33у + 133 = 0; 6) а) АВ = 15, АС = 25, ВС = 20;
б) АВ: 3х + 4у - 20 = 0; АС: 7х - 24у - 180 = 0; ВС: 4х - 3у + 15 = 0;
в) 24х + 7у - 35 = 0; г) x + 18y + 60 = 0; д) AE = 5
13
; е) 9x - 13y -
- 35 = 0; ж) S = 150 кв. ед.; з) cos∠C = 0,352; и) М(0; -10/3);
7) В(6; 0); 2x + 3y - 12 = 0.
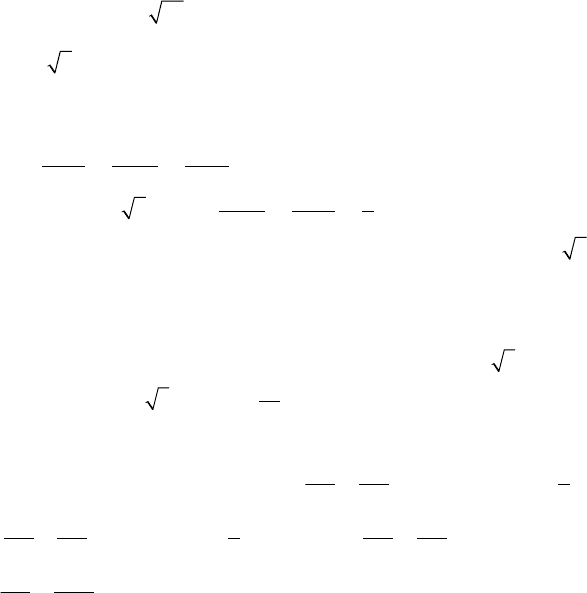
3.2. Плоскость в пространстве
8) θ = arccos(6/
95
); 9) x - 2y + z - 7 = 0; 10) x + y - 3 = 0;
11) a) z - 4 = 0; б) 3х + 2у = 0; в) 10х + z - 14 = 0;
12) 3/(2
6
); 13) y - z - 3 = 0; 14) (3; 5; 7).
3.3. Прямая в пространстве.
Взаимное расположение прямой и плоскости
15)
xyz+
=
-
=
-
-
1
4
2
0
3
8
;
x = 4t - 1, y = 2, z = -8t + 3;
16) ϕ = arccos(2
7
/7); 17)
xyz-
=
+
=
2
2
1
74
;
x = 2t + 2, y = 7t - 1,
z = 4t; 18) (2; 3; 1); 19) (7; 0; 1); 20) sinθ = 1/
6
;
21) A = -10, l = -1/5; 22) A = -1; 23) 16x - 27y + 14z -
- 159 = 0.
4. Аналитическая геометрия на плоскости: кривые II порядка
1) а) а = 5, b = 3, F
1,2
(±4; 0), e = 4/5; б) a =
5
, b = 2,
F
1,2
(±3; 0), e = 3
5
/5;
yx=±
2
15
;
в) b = 4, a = 3, F
1,2
(0; ±5),
e = 5/4, y = ±4x/3; 2) a) p = 2, F(-1; 0); б) p = 1/4, F(0; 1/8);
3) C(2; -3), R = 4; 4) a)
′
+
′
=
xy
22
95
1;
б)
′
=-
′
xy
2
1
2
;
в)
′
-
′
=
xy
22
45
1;
г)
′
=
′
yx
2
1
2
;
5) a)
-
′
+
′
=
xy
22
42
1,
ϕ = 45°;
б)
′
+
′
=
xy
22
2
3
2
1,
ϕ = 135°.
5. Аналитическая геометрия в пространстве:
поверхности II порядка
1) С(2; 1; -1), R = 5; 2) а) эллипсоид; б) гиперболический ци-
линдр; в) однополостный гиперболоид; г) двухполостный гипер-
болоид; д) эллиптический параболоид; е) гиперболический пара-
болоид.

73
Глава 2
введение в математический анализ
6. Функции одной Переменной.
Элементарные Функции
опорный конспект № 6
6.1. Элементы теории множеств
A ∪ B = {x: x ∈ A ∨ x ∈ B}
A ∩ B = {x: x ∈ A ∧ x ∈ B}
A\B = {x: x ∈ A ∧ x ∉ B}
B ⊂ A ⇒ A\B =
B
6.2. Функции
y = f(x), x ∈ X, y ∈ Y ⇔ X →: Y: ∀x ∈ X ∃! y ∈ Y, X = D( f ) — область
определения, Y = E( f ) — область значений, x — независимая пере-
менная (аргумент), y — зависимая переменная (функция),
R = (-∞, +∞)
6.3. Основные элементарные функции.
Элементарные функции
1) y = c, c — const
2) y = x
n
, n ∈ R\{0} — cтепенная, E( f )
форма графика зависят от n
3) y = a
x
, a > 0, a ≠ 1 — показательная,
D( f ) = (-∞, +∞), E( f ) = (0, +∞)
4) y = log
a
x, a > 0, a ≠ 1 — логарифмическая, D( f ) = (0, +∞),
E( f ) = (-∞, +∞)
5) Тригонометрические:
y = sinx, D( f ) = (-∞, +∞), E( f ) = [-1, +1];
y = cosx, D( f ) = (-∞, +∞), E( f ) = [-1, +1];
y = tgx, D( f ) = R\{π/2 + kπ}, k = 0, ±1, ±2, ..., E( f ) = (-∞, +∞);
y = ctgx, D( f ) = R\{kπ}, k = 0, ±1, ±2, ..., E( f ) = (-∞, +∞)
6) Обратные тригонометрические:
y = arcsinx, D( f ) = [-1, +1], гл. значение y ∈ [-π/2, π/2];
y = arccos x, D( f ) = [-1, +1], гл. значение y ∈ [0, π];
y = arctg x, D( f ) = (-∞, +∞), гл. значение y ∈ (-π/2, π/2);
y = arcсtg x, D( f ) = (-∞, +∞), гл. значение y ∈ (0, π)
Сложная функция (суперпозиция функций) y = ϕ[ψ(x)] ⇔
⇔ y = ϕ(z), z = ψ(x), x ∈ X, z ∈ Z, y ∈ Y

74
Элементарные функции (э.ф.) — записанные одной формулой,
составленной из основных э.ф. с помощью символов (+), (-), (×),
(:) и операции суперпозиции

75
Задачи к разд. 6.1
Задача 1. А — множество четных положительных чисел, В —
множество нечетных положительных чисел. Определить А ∩ В,
А ∪ В.
Решение: А ∩ В = ∅, А ∪ В = N = {1, 2, …, n, …}.
Задача 2. А — множество всех чисел, делящихся на 2, В — мно-
жество всех чисел, делящихся на 5. Определить А ∩ В.
Решение: А ∩ В определяет множество всех чисел, делящихся на
2 и на 5, т.е. А ∩ В — это множество всех чисел, делящихся на 10.
Задача 3. А = {1, 2, 3, 4, 5}, B = {3, 5}. Определить А\В, В\А.
Решение: А\В = {1, 2, 4}, B\A = ∅.
Задачи для самостоятельного решения
1) А = {1, 2, 3}, B = {2, 3, 4}; A ∪ B, A ∩ B, A\B — ?
2) Если А — множество студентов первого курса, В — множество
студенток первого курса, то какое из суждений верно: а) В ⊂ А;
б) А ⊂ В?
Задачи к разд. 6.2, 6.3
Задача 1. Найти области определения D( f ) функций:
а)
yx=-1
2
;
б)
y
xx
x
=
-+
-
25
8
2
3
lg()
.
Решение: а) функция определена для значений переменной х,
удовлетворяющей условию 1 - х
2
≥ 0, (1 - х)(1 + х) ≥ 0, т.е.
х ∈ [-1, 1] (рис. 6.1) ⇒ D( f ) = [-1, 1];
Рис. 6.1
б) переменная х должна удовлетворять условиям
x
x
x
xx x
x
x
+>
->
⇒
>-
-++>
>-
->
50
80
5
2240
5
20
32
,
,
,
()(),
,
,
>-
<
x
x
5
2,
т.е. D( f ) = (-5; 2).
Задача 2. Найти множество значений E( f ) функций:
а) y = x
2
- 6x + 5; б) y = 3 + 2sin x; в)
yx=-16
2
.

76
Решение: а) y = x
2
- 6x + 5 = (x - 3)
2
- 4 ⇒ y ∈ [-4, +∞), E( f ) =
= [-4, +∞);
б) поскольку -1 ≤ sin x ≤ 1 ⇒ -2 ≤ 2 sin x ≤ 2 ⇒ y ∈ [1, 5], E( f ) =
= [1, 5];
в) D( f ): 16 - x
2
≥ 0, x
2
≤ 16, -4 ≤ x ≤ 4, D( f ) =
= [-4; 4] ⇒ E( f ) = [0, 4]. Так как y
2
= 16 - x
2
⇒
⇒ y
2
+ x
2
= 16 — уравнение окружности ради-
усом 4,
yx=-16
2
— верхняя половина
окружности (рис. 6.2).
Задача 3. Найти основные периоды T функций: а) f(x) = cos8x;
б) f(x) = sin6x + tg4x.
Решение: а) период функции соsx T
1
= 2π ⇒ T = 2π/8 = π/4;
б) функции sin6x и tg4x имеют периоды T
1
= 2π/6 = π/3 и
T
2
= π/4 соответственно. Основной период функции f (x) =
= sin6x + tg4x есть наименьшее общее кратное чисел π/3 и π/4,
т.е. Т = π.
Задача 4. Установить четность или нечетность функций:
а) f(x) = 2
x
+ 2
-x
; б) f(x) = x
2
+ 5x; в)
fx
x
x
() lg .=
+
-
3
3
Решение: а) f(-x) = 2
-х
+ 2
x
= f(x) ⇒ функция четная;
б) f(-x) = x
2
- 5x ≠ -f(x) ≠ f(x) ⇒ функция f(x) ни четная, ни
нечетная;
в)
fx
x
x
x
x
x
x
x
x
fx()lg lg lg lg ()-=
-+
--
=
-
+
=
+
-
=-
+
-
=-
-
3
3
3
3
3
3
3
3
1
⇒⇒ fx()
⇒ f(x) — нечетная функция.
Задача 5. Записать элементарную функцию
y
x
= 2
2
sin
в виде це-
почки основных элементарных функций.
Решение: Обозначим sinx
2
= z, x
2
= t. Тогда имеем y = 2
z
,
z = sint, t = x
2
.
Задачи для самостоятельного решения
Найти области определения функций:
3) y = x
2
+ 2x - 5; 4)
y
xx
=
-+
1
32
2
;
5)
y
xx
=
+-
1
6
2
;
6)
yx
x
=-+
-
14
31
2
arcsin ;
7)
yx xx=-+-++11 1
2
;
8) y = lgsinx.
Рис. 6.2

77
Найти множества значений функций:
9) y = -x
2
+ 8x - 13; 10)
y
x
=
-
4
2
;
11) y = 1 - 3cosx.
Найти основные периоды функций:
12) f(x) = lgcos2x; 13) f(x) = -2cos(x/3) + 1; 14) f(x) = tg3x +
+ cos4x.
Установить четность или нечетность функций:
15)
fx xx x() sin;=+
2
3
2
16)
fx x
x
() ;=-5
2
e
17) f(x) = x
4
sin7x;
18) f(x) = lgcos x.
19) Дано
yz= ,
z = sint, t = x
2
. Найти у(х).
20) Дано y = sinx, ν = lg y,
u =+1
2
ν .
Найти u(x).
21) Следующие сложные функции представить в виде цепочки
из основных элементарных функций:
а)
yx= sin(cos);
б) y = lgtg2
x
;
в)
y
x
= arcsin .e
3
22) f(x) = x
3
- x, ϕ(x) = sin2x. Найти:
а) f(ϕ(π/2)); б) ϕ( f(1)); в) f(ϕ(x)); г) f( f(x)); д) ϕ( f(x)).
7. Пределы Функции одной Переменной
опорный конспект № 7
7.1. Предел последовательности
x
n
= f(n), n ∈ N,
lim
x
n
xa
→∞
=
⇔
⇔ ∀e > 0 ∃N = N(e):
n > N ⇒|x
n
- a| < e
Геометрически:
n > N ⇒ x
n
∈ (a - e, a + e)
7.2. Предел функции в точке
lim()
xa
fx b
→
=
⇔ ∀e > 0 ∃δ = δ(e):
0 < |x - a| < δ ⇒ | f(x) - b| < e
Геометрически:
x ∈ (a - δ, a + δ) ⇒
⇒ f(x) ∈ (b - e, b + e)
7.3. Бесконечно малые и бесконечно большие функции
α(x) - б.м., x → a ⇔
lim(),
xa
x
→
=α 0

78
f(x) - б.б., x → a (
lim()
xa
fx
→
=∞
) ⇔ ∀M > 0 ∃δ = δ(M):
|x - a| < δ ⇒ |f(x)| > M
Связь б.м. и б.б.: 1/0 = ∞, 1/∞ = 0
7.4. Леммы о б.м.
Л.1: α, β, γ — б.м., x → a ⇒ (α + β - γ) — б.м., x → a
Л.2: |f(x)| < M, α(x) — б.м., x → a ⇒ f(x)α(x) — б.м., x → a
7.5. Теоремы о пределах
Т.1:
lim,
xa
cc
→
=
c — const
T.2 (о связи функции с ее lim):
f(x) = b + α(x), α(x) — б.м., x → a ⇔
lim()
xa
fx b
→
=
Т.3:
lim[ () ()]lim () lim()
xa xa xa
fx fx fx fx
→→→
±= ±
12 12
Т.4:
lim[ () ()]lim ()lim()
xa xa xa
fx fx fx fx
→→→
⋅= ⋅
12 12
Т.5:
lim
()
()
lim()
lim()
,lim ()
xa
xa
xa
xa
fx
fx
fx
fx
fx
→
→
→
→
=≠
1
2
1
2
2
0
7.6. неопределенности
0
0
01
∞
∞
⋅∞ ∞-∞
∞
,,{},{ }, {}
I замечательный предел:
lim
sin
x
x
x
→
=
=
0
0
0
1
II замечательный предел:
lim{}lim()
n
n
n
n
n
ne
→∞
∞
→
+
== +=1
1
11
0
1
7.7. Сравнение б.м.
lim
()
()
(),
,,
xa
x
x
oxa
A
→
=
⇔= →
≠∞⇔
⇔
∃⇔
α
β
αβ
αβ
αβ
0
0 — одного порядка
1 ∼
ααβ,—несравнимы
Т: α(x) ~ α′(x), β(x) ~ β′(x), x → a ⇒
lim
()
()
lim
()
()
xa xa
x
x
x
x
→→
=
′
′
α
β
α
β

79
Задачи к разд. 7.1, 7.2
Задача 1. Доказать, что
lim.
n
n
n
→∞
+
=
1
1
Решение: Пусть e > 0: |x
n
- 1| < e, т.е.
n
nn
n
+
-=
+
<⇒>
-
1
1
1
1
1
e
e
e
.
n
nn
n
+
-=
+
<⇒>
-
1
1
1
1
1
e
e
e
.
Таким образом, за N можно взять целую часть числа (1 - e)/e,
т.е. N = [(1 - e)/e]. Неравенство |x
n
- 1| < e будет справедливо
при всех n > N, что и требовалось доказать.
Задача 2. Доказать, что
lim.
n
n
n
→∞
-
=
31
3
1
Решение: ∀e > 0
31
3
11
1
3
1
1
3
n
nnn
-
-=- -= <e,
3
n
> 1/e или
log
3
3
n
> log
3
(1/e) ⇒ n > log
3
(1/e); таким образом, если выбрать
N = [log
3
(1/e)], то при n > N будет выполняться неравенство
31
3
1
n
n
-
-<e,
что и требовалось доказать.
Задача 3. Доказать, что число 2 не является пределом последо-
вательности с общим членом
u
n
n
n
=
+
+
21
42
при n → ∞.
Решение: Рассмотрим величину
u
n
n
n
n
n
n
n
-=
+
+
-=-
+
+
=
+
+
2
21
42
2
63
42
63
42
.
u
n
n
n
n
n
n
n
-=
+
+
-=-
+
+
=
+
+
2
21
42
2
63
42
63
42
.
Решим относительно n неравенство
63
42
n
n
+
+
<e.
63
42
4221
42
1
1
2
1
n
n
nn
n
+
+
=
++ +
+
=+ >
()
, и следовательно, оно не мо-
жет быть меньше произвольно заданного e > 0, например
e = 0,5.
Следовательно, число 2 не является пределом последовательно-
сти
21
42
n
n
+
+
.
Задача 4. Доказать, что f(x) = 3x - 2 в точке х = 1 имеет пре-
дел, равный 1, т.е.
lim( ).
x
x
→
-=
1
321

80
Решение: ∀e > 0 |3x - 2 - 1| = |3(x - 1)| = 3|x - 1| < e ⇒
⇒ | x - 1| < e/3 ⇒ если взять δ ≤ e/3, то из |x - 1| < δ ⇒
⇒ |(3x - 2) - 1| < e, что и требовалось доказать.
Задача 5. Доказать, что
limsin
x
x
x
→
=
0
1
0
(х ≠ 0).
Решение: ∀e > 0 |xsin(1/x) - 0| = |xsin(1/x)| < e |xsin(1/x)| =
= |x||sin(1/x)| ≤ |x| < e (|sin(1/x)| ≤ 1 при х ≠ 0). Следовательно,
если взять δ ≤ e, то из |x| < δ будет вытекать |xsin(1/x)| < e, что и
требовалось доказать.
Задачи для самостоятельного решения
1) Доказать, что последовательность 1, 17/14, 37/29, 65/50,
101/77, …, (4n
2
+ 1)/(3n
2
+ 2) при n → ∞ имеет предел, равный
4/3.
2) Доказать:
а)
lim( );
n
n
→∞
+=2
1
2
б)
lim.
n
n
n
→∞
-
+
=
43
1
4
3) Доказать, что при n → ∞ последовательность 1, 1/3, 1/5, …,
1/(2n - 1) является бесконечно малой.
4) Доказать, что: а)
lim( );
x
x
→
-=
2
351
б)
lim.
x
x
→
=
2
2
4
Задачи к разд. 7.3–7.7
Задача 1. Вычислить: а)
lim;
x
x
x
→
+
+
1
52
23
б)
lim( );
x
x
x
→2
3
2
в)
lim.
x
x
x
→
+
-
1
2
31
1
Решение: а) пользуясь теоремами о пределах (разд. 7.5 опорного
конспекта (ОК)), для нахождения данного предела достаточно
подставить в функцию предельное значение аргумента:
lim
x
x
x
→
+
+
=
1
52
23
=
⋅+
⋅+
=
51 2
21 3
8
5
;
б) переходим к пределу в основании и показателе:
lim( )
x
x
x
→
=
2
3
2
===
→
→
lim( );
lim
x
x
x
x
2
4
361296
2
2
в) так как
lim( ),
x
x
→
- =-=
1
2
1110
то теорема о пределе частного
не подходит, но можно применить теорему о связи бесконечно
малой и бесконечно большой величин (разд. 7.3 ОК):
lim
x
x
x
→
+
-
=
1
2
31
1
=
=∞
4
0
.
