Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Нуриева С.Н., Дегтярева О.М. Математика в примерах и задачах
Подождите немного. Документ загружается.

91
Глава 3
диФФеренциальное исчисление
Функции одной Переменной
9. диФФеренцируемые Функции
одной Переменной
опорный конспект № 9
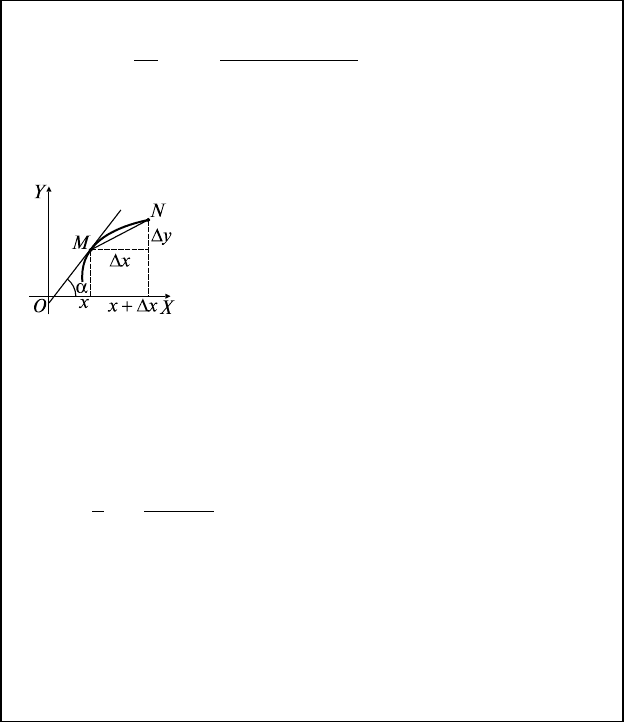
9.1. Определение производной, ее физический смысл
′
==
+-
→→
y
y
x
fx xfx
x
xx
limlim
()()
∆∆
∆
∆
∆
∆
00
s = s(t) — закон неравномерного прямолинейного движения ⇒
скорость v = s′(t)
9.2. Геометрический смысл y′
f ′(x) = tg α = k — угловой коэффициент каса-
тельной в т. М(x, y)
y - y
0
= f ′(x
0
)(x - x
0
) — касательная в
т. М
0
(x
0
, y
0
)
9.3. Существование производной и непрерывность
∃f ′(x) ⇒ f (x) — непрерывна
9.4. Свойства операции дифференцирования
1) (c)′ = 0, c = const;
2) (u + v - w)′ = u′ + v′ - w′;
3) (uv)′ = u′v + uv′, (cu)′ = cu′;
4)
u
v
uv vu
v
′
=
′
-
′
2
,
v ≠ 0
9.5. Производная сложной функции
(ϕ[ψ(x)])′ = ϕ′[ψ(x)]ψ′(x)
Логарифмическая производная (lny)′ = y′/y
Производная показательно-степенной функции
[u(x)
v(x)
]′ = v
.
u
v-1
u′ + u
v
lnu ⋅
v′

92
9.6. Производные основных элементарных функций
(x
n
)′ = nx
n-1
, (a
x
)′ = a
x
lna, (e
x
)′ = e
x
,
(log )
ln
,
a
x
xa
′
=
1
(lnx)′ = 1/x,
(sinx)′ = cosx, (cosx)′ = -sin x,
(tgx)′ = 1/cos
2
x, (ctgx)′ = -1/sin
2
x,
(arcsin) ,x
x
′
=
-
1
1
2
(arccos) ,x
x
′
=-
-
1
1
2
(arctg ),x
x
′
=
+
1
1
2
(arcctg) .x
x
′
=-
+
1
1
2
9.7. Дифференциал
dy = f ′(x)∆x или dy = f ′(x)dx, где dx = ∆x — обозначение
dy ~ ∆y, ∆x → 0 ⇒ f(x + ∆x) ≈ f(x) + dy
Свойства дифференциала:
1
0
. dc = 0, c = const.
2
0
. d(u + v) = du + dv.
3
0
.
d(uv) = vdu + udv.
4
0
. d(cu) = cdu.
5
0
.
d
ddu
v
vu uv
v
=
-
2
,
v ≠ 0.
6
0
. dϕ[ψ(x)] = ϕ′[ψ(x)]dψ(x) — инвариантность формы dy
9.8. Производные и дифференциалы высших порядков
f
(n)
(x) = [ f
(n-1)
(x)]′, d
n
y = d[d
n-1
y] = f
(n)
(x)dx
n
9.9. Производные параметрически заданной функции
xxt
yyt
y
yt
xt
y
y
xt
xx
xt
=
=
′
=
′
′
′′
=
′′
′
(),
(),
()
()
,
()
()
Задачи к разд. 9.1–9.6
Задача 1. Исходя из определения производной вычислить:
а) y′(8), если
yx=
3
;
б) y′(1), если
yx x
x
x
=+ -
+
()arcsin .1
1
Решение: а) по определению производной
′
=
′
==
+-
=
=
=
=
→→
yx
y
x
x
x
x
xx
() () limlim
lim
8
880
0
3
8
00
33
∆∆
∆
∆
∆
∆
∆∆
∆
∆
∆∆ ∆
∆∆
x
x
x
xx x
xx
→
→
+-
++++
=
=
+++
0
2
3
3
0
2
3
3
88
8284
1
828
(( ))
lim
(( ) ++
=
4
1
12
)
;
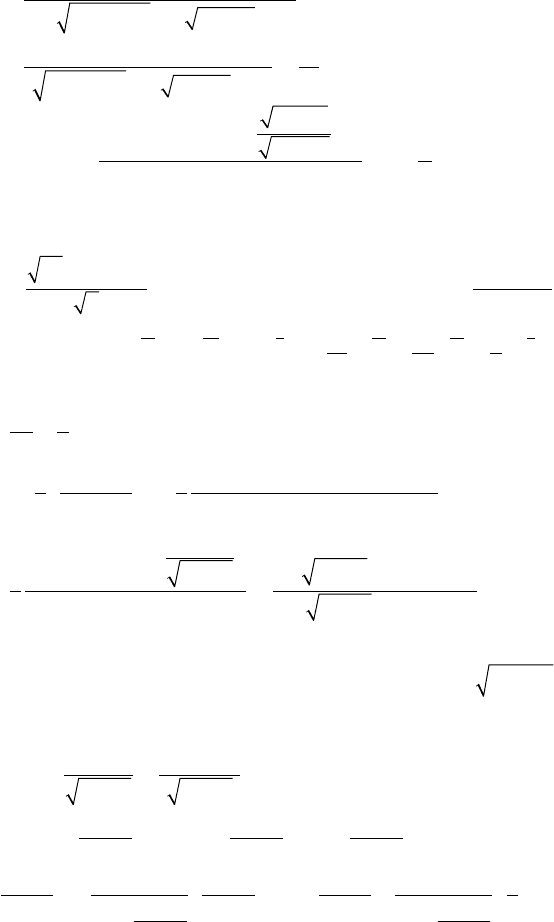
93
′
=
′
==
+-
=
=
=
=
→→
yx
y
x
x
x
x
xx
() () limlim
lim
8
880
0
3
8
00
33
∆∆
∆
∆
∆
∆
∆∆
∆
∆
∆∆ ∆
∆∆
x
x
x
xx x
xx
→
→
+-
++++
=
=
+++
0
2
3
3
0
2
3
3
88
8284
1
828
(( ))
lim
(( )
++
=
4
1
12
)
;
б)
′
=
++
+
+
-
=+
→
y
xx
x
x
x
x
() lim
arcsin
.1
1
1
2
1
1
4
0∆
∆∆
∆
∆
∆
π
Задача 2. Вычислить производные следующих функций, ис-
пользуя правила дифференцирования и таблицу производных:
а)
y
xx
x
=
+-
2
3
5
5
34
;
б) y = x
3
arctgx; y′(1) = ? в)
y
x
x
=
e
3arccos
.
Решение: а)
′
=+-
(
)
′
=++
-- -
yx xx xxx
7
15
24
5
1
5
8
15
19
5
6
5
34
7
15
72
5
4
5
;
б) y′ = (x
3
)′arctgx + x
3
(arctgx)′ = 3x
2
arctgx + x
3
/(1 + x
2
);
y′(1) =
3
4
1
2
π
+ ;
в)
′
=
′
=
′
-
′
=y
x
xx
x
xx x
1
3
1
3
2
ee e
arccos
()arccos(arccos)
arccos
==
--
-
=
-+
-
1
3
1
11
31
2
2
2
2
e
e
e
x
x
x
x
x
x
xx
x
arccos
arccos
(arccos)
aarccos
.
2
x
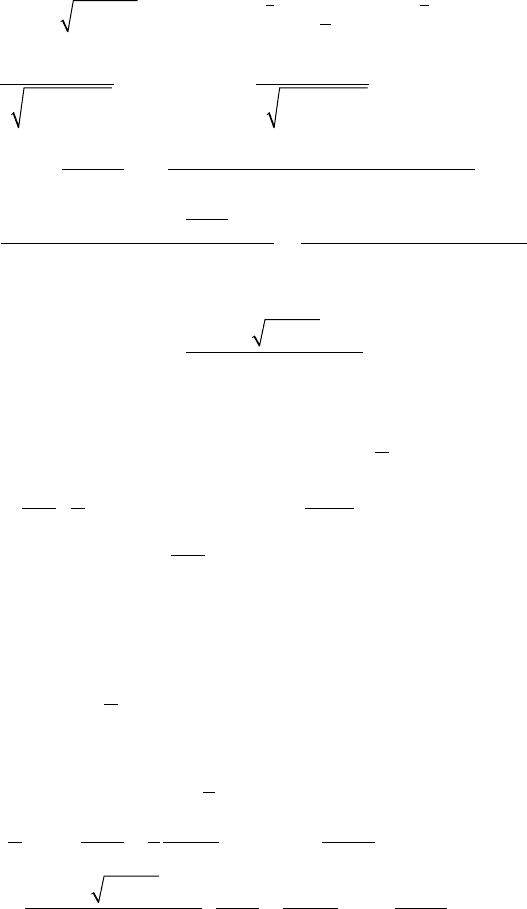
Задача 3. Вычислить производные сложных функций:
а) y = arcsin
2
x; б) y = x tg((3x + 1)/5); в)
yx
x
=+e
2
3
;
г) y = (x
3
+ 3)/lnsinx.
Решение: а) y′ = ((arcsinx)
2
)′ = 2arcsinx ⋅ (arcsinx)′ =
= 2arcsinx ⋅
1
1
2
1
22
-
=
-x
x
x
arcsin
;
б)
′
=
+
′
=
′
+
+
+
′
=yx
x
x
x
x
x
tg ()tg tg
31
5
31
5
31
5
=
+
+
+
+
′
=
+
+
+
⋅tg
cos
tg
cos
;
31
5
1
31
5
31
5
31
5
31
5
3
5
22
x
x
x
xxx
x
94
в)
′
=+
()
′
=+
(
)
′
=+
(
)
+
(
)
′
=
-
yx xxx
xx xx
ee ee
22 22
3
1
3
2
3
1
3
=
+
(
)
+
′
()
=
+
+
(
)
1
3
1
12
3
2
2
2
2
2
3
2
2
3
x
x
x
x
x
x
x
x
e
e
e
e
() ;
г)
′
=
+
′
=
+
′
-+
′
=y
x
x
xxxx
x
33 3
2
33 3
lnsin
()lnsin( )(lnsin )
ln sin
=
-+
=
-+
33
1
33
23
2
23
2
xxx
x
x
x
xxxx
lnsin( )
sin
cos
ln sin
lnsin( )ctg
ln s
iin
.
x
Задача 4. Вычислить производные функций:
а)
yx
x
= (ln);
2
б)
y
xx
x
x
=
+-⋅
-
()
()
.
13
1
32 2
25
e
Решение: а) первый способ — логарифмическое дифференциро-
вание:
ln ln(ln) (ln) (ln(ln )) ln(ln)yx yx x
y
yx x
x
=⇒
′
=
′
⇒⋅
′
=+
2
2
1
2
+⋅⇒
′
=+⇒
′
=x
xx
yyxxx
xx
y
22
11
2
1
ln
(lnln
ln
)
=+(ln)(lnln
ln
).xxx
x
x
x
2
2
Второй способ — производная показательно-степенной
функции:
′
=
()
′
=
′
+
′
=
-
yxxx xx xx
xx x
(ln) (ln) (ln) (ln) ln(ln)()
22 2
21 2
=+⋅= +
-
xx
x
xxxxxx
xx x21
22 2
1
22(ln) (ln) ln ln (ln) ln ln
+
-
xx
x
(ln) ;
2
1
б)
(ln) (ln( )ln( )lnln( ))yx xx x
′
=++-+- -
′
⇒31
1
2
32 51
22
e
⇒⋅
′
=
+
+
-
⋅+-
-
⋅
13
1
1
2
1
3
225
1
1
2
22
y
y
x
x
x
x
x;
′
=
+-⋅
-
+
+
-
+-
-
y
xx
x
x
x
x
x
x
x
()
()
.
13
1
3
1
3
2
10
1
32 2
25 22
e
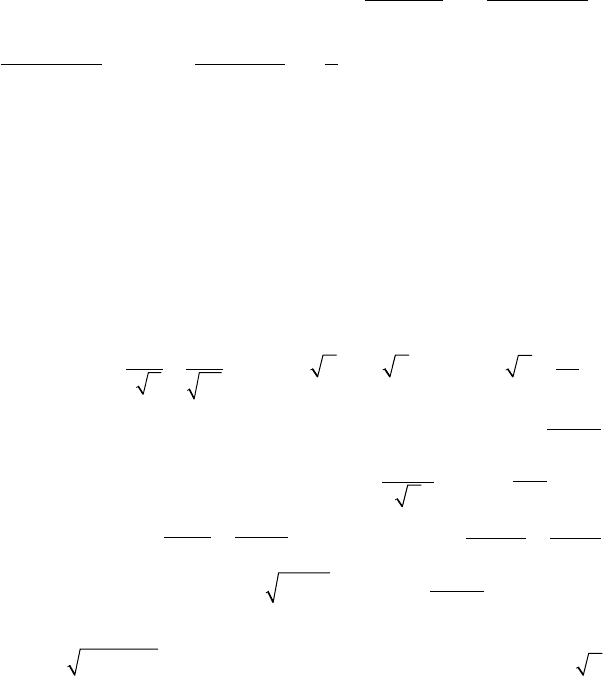
95
Задача 5. Тело массой 3 кг движется прямолинейно по закону
s = 1 + t + t
2
(s — в см, t — в с). Определить кинетическую энер-
гию тела через 5 с после начала движения.
Решение: Кинетическая энергия E = mv
2
/2, v = s′ = 2t + 1,
v(5) = 11 (см/с), E = 3 ⋅ 121/2 = 181,5 эрг.
Задача 6. Составить уравнение касательной и нормали к графи-
ку функции y = 8a
3
/(4a
2
+ x
2
) (a = const) в точке с абсциссой
2a.
Решение: Уравнение касательной приведено в ОК, разд. 9.2.
Вычисляем:
y(2a) = 8a
3
/(4a
2
+ 4a
2
) = a,
′
=
+
′
=
-⋅
+
=
-
+
y
a
ax
ax
ax
ax
ax
8
4
82
4
16
4
3
22
3
222
3
222
()()
,
′
=
+
′
=
-⋅
+
=
-
+
y
a
ax
ax
ax
ax
ax
8
4
82
4
16
4
3
22
3
222
3
222
()()
,
′
=
-⋅
=- ⇒ya
aa
a
()
()
2
16 2
8
1
2
3
22
y - a = -(x - 2a)/2 ⇒
⇒ y + x/2 - 2a = 0 — уравнение касательной.
Нормаль — прямая, перпендикулярная касательной, поэтому
угловой коэффициент нормали k
н
= -1/k
кас
= 2. Уравнение нор-
мали: y - a = 2(x - 2a) ⇒ y - 2x + 3a = 0.
Задачи для самостоятельного решения
Найти производную у′ заданной функции или у′(х
0
), используя
правила дифференцирования и формулу нахождения производной
сложной функции:
1)
yx
x
x
=- +2
1
5
3
3
2
3
;
2)
yxxx=+53
3
;
3)
yx
x
=-
×6
1
3
2
× (7x - 3); 4) y = 3x
4
+ 4x
3
- 5x
2
- 5x - 2, у′(0) = ? 5)
y
x
x
=
-
+
2
2
1
1
,
у′(1) = ? 6) y = xarctgx, y′(1) = ? 7)
y
x
x
=
sin
;
2
8)
y
x
x
=
ln
,
у′(e),
y′(1/e) = ?; 9)
y
x
x
=
+
+
+
1
2
3
1
2
,
у′(0) = ? 10)
y
x
x
=+
sin
sin
;
2
3
3e
3
11) y = cosx
5
ln
2
x; 12)
yx= tg ;
32
5
13)
y
x
x
=
sin
cos
,
5
3
y ′(π) = ?;
14)
y
x
= e
2
;
15)
y
x
=
-
10
15
3
;
16)
y
x
= 5
2
sin
;
17) y = x
2
e
-2x
, y′(1) = ?
18)
yx= arcsin ;
2
19) y = x
2
arctg
5
x; 20)
yx= arccos;
5
96
21)
yx
x
= arctg,
2
1
y′(1) = ?; 22)
y
x
x
=
ln
;
2
23)
yx x=+log( );
3
3
24) y = ln
4
sinx; 25) y = ln
2
(x
2
- 4x), y′(5) = ?
Найти y′(x) или y′(x
0
), используя логарифмическое дифферен-
цирование:
26) y = x
x+1
;
27)
yx
x
=
+
(arctg );
2
1
28)
yx
x
= () ,
cos
3
3
y ′(π) = ?;
29)
y
xx
x
=
+-
+
()()
()
;
6545
27
3
4
2
3
30)
y
xx
x
=
-
+
()cos
()
,
1
1
2
23
5
y ′(0) = ?;
31) y = x
sin2x
; 32)
y
x
xx
=
-
ln
sin
;
3
12
33)
y
x
x
=
1
arcsin
.
Найти y′(x) или y′(x
0
):
34)
yx
x
=-(sin );e
2
3
35)
y
x
xx
=
+
++
ln()
,
33
35
2
3
y ′(0) = ? ;
36)
y
x
x
xx
x
x
x
=+ -+
23 4
5
2
3
,
y ′(1) = ?; 37) y = xe
1+tgx
; 38) y =
= x
2
sinx + xlog
3
x, y′(1) = ?; 39)
yx
x
= (cos );
3
40)
y
x
=
3
2
4
3
arctg
,
y ′(2) = ?; 41)
ye
x
=
sin
;
42)
yx xx=+ --()() ;214
2
5
23
43)
y
xx
=---ee11arctg;
44)
y
x
=-
ln tg ;
π
42
45)
y
x
x
=+2
8
1
8
2
ln tg
cos
;
46) y = sin
2
(tgx); 47)
yx=+arcsin();21
3
48)
y
xx
x
=
-+
+
3121
15 1
3
5
;
49)
yx
x
= (sin ).
Показать, что функции y = f(x) удовлетворяют данным уравне-
ниям вида F(x, y, y′) = 0:
50) y = xsinx — уравнению y ′/cosx - x = tgx; 51) y = (x +
+ 1)e
x
— уравнению y′ - y = e
x
; 52)
yxxc=-+2
2
ln
— уравне-
нию xyy′ = 1 - x
2
.
Найти уравнения касательной и нормали к графику функции
y = f(x) в точке М
0
(x
0
, y
0
):
53) y = 2x
2
- 6x + 3, x
0
= 1; 54) y = 1/(1 + x
2
), x
0
= 2;
55)
yxx=+62
3
,
x
0
= 64.
97
56) Точка движется прямолинейно по закону s = t
3
/3 + 2t
2
- t,
s — расстояние (в м), t — время (в с). Найти скорость движения
через 1 с после начала движения.
57) Точка движется прямолинейно по закону s = (t
4
- 4t
3
+
+ 2t
2
- 12t)/4, s — расстояние (в м), t — время (в с). В какой мо-
мент времени точка остановится?
58) Тело массой 25 кг движется прямолинейно по закону
s = ln(1 + t
2
). Найти кинетическую энергию тела (mv
2
/2) через 2 с
после начала движения.
59) Определить силу тока в конце пятой секунды, если известно,
что количество электричества, протекшее через проводник начиная
с момента времени t = 0 дается формулой Q = 2t
2
+ 3t + 1 (куло-
нов).
Задачи к разд. 9.7–9.9
Задача 1. Найти дифференциал dу, если: a)
y
x
x
= 5
1
2
arccos;
б) y = x
arcsinx
.
Решение:
а)
ddy
x
x
x
x
x
x
xx
=
′
=
=⋅ +-
-
5
1
25 5
1
5
1
1
1
2
22
arccos
ln arccos
22
2
2
1
52 5
11
2
-
=
=+
-
x
x
x
x
xx
x
d
ln arccos
11
dx;
б)
ddyx x
xx xx
x
x
xx
=
′
=
=⋅⋅+
-
-
()
arcsin ln
arcsin
arcsin arcsin1
2
1
1
1
dx.
Задача 2. Вычислить приближенно arctg0,96.
Решение: Воспользуемся определением дифференциала (ОК,
разд. 9.7). Обозначим х
1
= х
0
+ ∆х = 0,96, х
0
= 1, тогда ∆х =
= -0,04. Так как f(x) = arctgx, то
′
=
+
fx
x
() ,
1
1
2
′
=f () ,1
1
2
f(0,96) =
= f(1) + f ′(1)∆x = arctg1 +
1
2
(-0,04) =
π
4
- 0,02 ≈ 0,765.
98
Задача 3. Найти производные указанного порядка:
а)
y
x
= e
2
,
y″ = ?; б) y = x
5
lnx, у′′′(1) = ? в) y = sin3x, y
(n)
= ?
Решение:
а)
′
=
(
)
′
=yx
xx
ee
22
2 ,
′′
=
′′
=
(
)
′
=+ ⋅= +yy xxxx
xxxx
() ();2222212
2222
2
eeee
′′
=
′′
=
(
)
′
=+ ⋅= +yy xxxx
xxxx
() ();2222212
2222
2
eeee
б) y ′ = (x
5
lnx)′ = 5x
4
lnx + x
5
1
x
= 5x
4
lnx + x
4
; y″ = (y′)′ =
= (5x
4
lnx + x
4
)′ = 20x
3
lnx + 9x
3
; y ′′′ = (y″)′ = (20x
3
lnx +
+ 9x
3
)′ = 60x
2
lnx + 20x
3
1
x
+ 27x
2
= 60x
2
lnx + 47x
2
; y ′′′(1) =
= 47;
в) y′ = cos3x ⋅ 3 = 3cos3x = 3sin(3x + π/2), y′′ = (3cos3x)′ =
= -9sin3x = 3
2
sin(3x + π), y′′′ = (-9sin3x)′ = -27cos3x =
= 3
3
sin(3x + 3π/2), y
IV
= (-27cos3x)′ = 3
4
sin(3x + 2π), …, y
(n)
=
= 3
n
sin(3x + nπ/2).
Задача 4. Найти дифференциал второго порядка d
2
y, если y =
= arcsin .x
Решение:
′
=
′
=
-
⋅=
-
yx
xx
xx
(arcsin) ;
1
1
1
2
1
2
2
d
2
y = y″dx
2
=
=
1
2
1
2
1
2
12
12
4
2
22
3
2
2
23
2
xx
xxxxx
x
xx
x
-
′
=- ⋅- -=-
-
-
-
ddd()()
()
..
Задача 5. Найти производные у′
х
, у′′
хх
параметрически заданной
функции:
а) x = acos
3
t, y = asin
3
t, a = const. Найти уравнение касатель-
ной в точке М
0
(х
0
, у
0
) при t
0
= π/4.
Решение: Используем формулы ОК, разд. 9.9:
′
=
′
′
=
′
′
=
-
=y
yt
xt
at
at
tt
tt
x
()
()
(sin )
(cos )
sincos
cos(sin)
3
3
2
2
3
3
--tg ,t
′′
=
′′
′′
=
-
′
′
=
-
-
y
yt
xt
t
at
t
at
xx
t
t
(())
(())
(tg)
(cos )
cos
cos(
3
2
2
1
3
ssin) cossin
.
tatt
=
1
3
4
Для определения уравнения касательной находим:
xxta
a
yyta
a
00
3
00
3
2
2
2
4
2
2
2
4
==
===
=() ,(),
′
=- =-yt
x
() tg ,
0
4
1
π
99
тогда уравнение касательной:
y
a
x
a
yx
a
-=--
⇒+-=
2
4
2
4
2
2
0.
Задачи для самостоятельного решения
Найти dy, если:
60) y = (1 + x - x
2
)
3
; 61) y = 5
lnsinx
; 62) y = (x
3
+ 1)
tg2x
;
63)
y
x
x
=
-
arctg;
3
2
2
1
64)
y
x
x
=
cos
.
Вычислить приближенно:
65)
801
3
,;
66) cos32°; 67) arcsin0,48; 68) lg10,08.
Найти производные указанного порядка:
69)
yx
x
=
-
e
2
,
y′′ = ?; 70) y = x
6
- 4x
3
+ 4, y
IV
(1) = ?;
71) y = e
2x
sin3x, y′′′(0) = ?; 72) y = ln
2
x, y ″ = ?; 73) y = e
3x
,
y
(n)
= ?; 74) y = sin
2
x, y
(n)
= ?
Найти дифференциалы второго порядка:
75) y = arctg3x; 76)
y
x
x
=
+1
;
77) y = tg(1 + x).
78) Показать, что функция y = 5e
-2x
- 3e
x
удовлетворяет урав-
нению y′′′ - 3y′ + 2y = 0.
79) Тело движется по прямой ОХ по закону x = t
3
/3 - 2t
2
+ 3t.
Определить скорость и ускорение движения. В какие моменты
времени тело меняет направление движения?
Найти у′
х
, у′′
хх
для функций, заданных параметрически:
80)
xatt
ya t
=-
=-
(sin ),
(cos );1
81)
xt
yt
=
=-
arcsin ,
ln();1
2
82)
xt
yt
t
t
=
=
e
e
cos,
sin.
83) Составить уравнения касательной и нормали к линии L:
x = sint, y = 2
t
при t
0
= 0.
100
10. исследование Функций
и Построение ГраФиков
опорный конспект №10
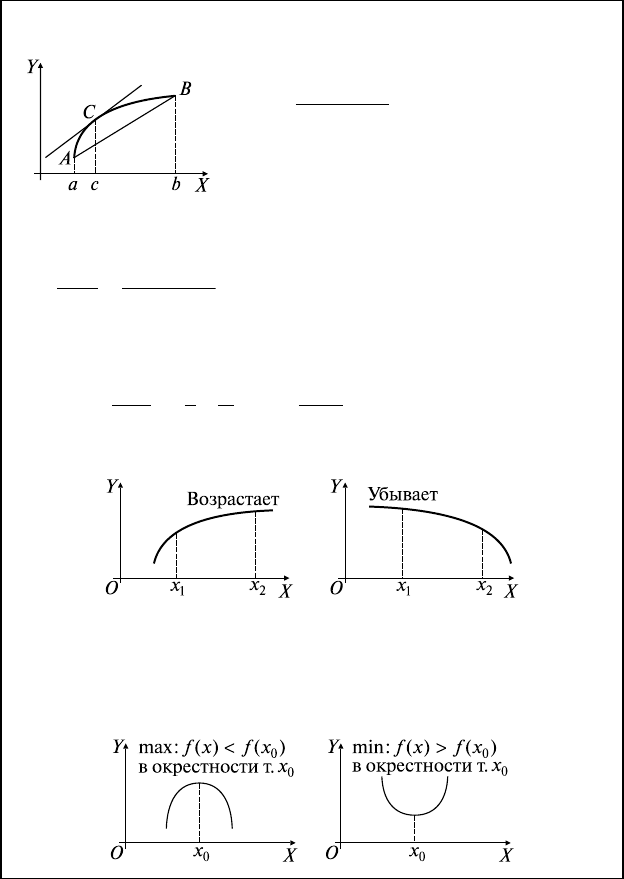
10.1. Основные теоремы дифференциального исчисления
Т. Лагранжа:
f(x) ∈ C
[a,b]
, ∃ f ′(x) ∀ x ∈ (a, b) ⇒ ∃с ∈ (a, b):
′
=
-
-
fc
fb fa
ba
()
() ()
Геометрическое истолкование:
k
кас. в т. С
= k
АВ
Т. Коши: f(x), g(x) ∈ C
[a,b]
, ∃ f ′(x), g′(x) ∀ x ∈ (a, b),
g′(x) ≠ 0 ⇒ ∃c ∈ (a, b):
′
′
=
-
-
fc
gc
fb fa
gb ga
()
()
() ()
() ()
10.2. Правило Лопиталя
Выполняются условия теоремы Коши в окрестности т. а ⇒
⇒=∨
∞
∞
=
′
′
→→
lim
()
()
lim
()
()
xa xa
fx
gx
fx
gx
0
0
10.3. Монотонность
Достаточный признак:
′
>⇒
<⇒
fx
ab fx
ab fx
()
(, )(),
(, )()
0
0
на
на
10.4. Экстремумы (э.)
