Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Нуриева С.Н., Дегтярева О.М. Математика в примерах и задачах
Подождите немного. Документ загружается.

111
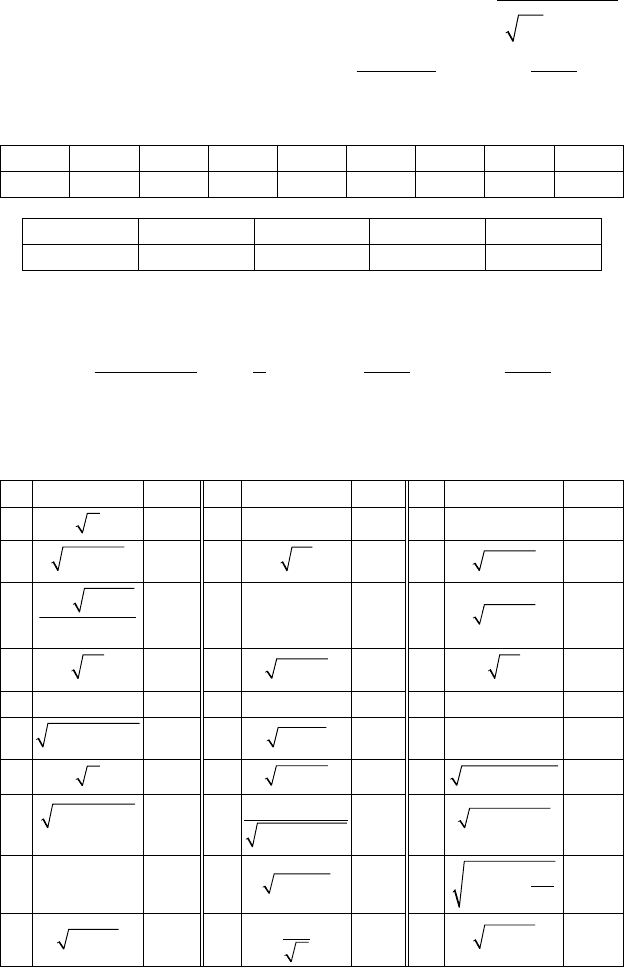
Задание 2. Вычислить производную функции
y
x
x
ij
k
=
+
(
)
-
ϕψ
σ
λ
[()]
,
()
1
1
где j, σ, k, a берутся из задания 1,
i
n
=
++
+
γδ
8
1;
λ
β
=
+
+
n
4
2,
а функции ϕ
i
(х), ψ
j
(х) находятся из таблицы:
i 1 2 3 4 5 6 7 8
ϕ
i
(x) sinx cosx tgx ctgx arcsinx arccosx arctgx arcctgx
j 1 2 3 4
ψ
j
(x) x
σ
a
x
log
a
x lnx
Задание 3. Написать уравнение нормали к y(х) = f(x) в точке
х
0
= ν, если:
fx
xx
x
r
nn n
r
r
() ,, ,=
++
+
=
+=
+
+=
+
+
µν
ν
µ
δ
ν
γ
7
2
6
1
3
11.
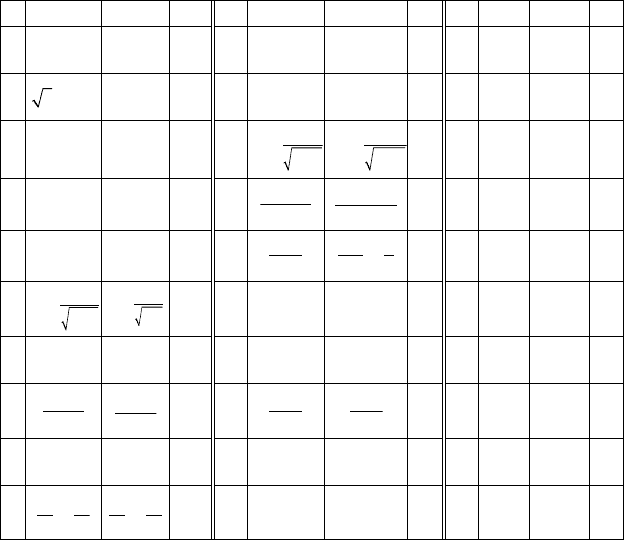
Задание 4. Приближенно с помощью дифференциала вычислить
значение y(х) в точке х
0
, если:
n y(x) x
0
n y(x) x
0
n y(x) x
0
1
x
3
0,98 11 x
23
0,998 21 x
7
2,003
2
xx
3
3
7+
1,012 12
x
3
4
15,95 22
43x -
2,98
3
xx+-5
2
2
0,98 13 x
6
2,007 23
57
3
x +
4,003
4
x
2
3
27,17 14
52
3
x +
4,93 24
x
3
5
31,94
5 arcsinx 0,007 15 x
7
1,996 25 ln(1 + 4x) 0,007
6
xx
2
3
25++
0,97 16
51
4
x +
2,993 26 x
4
3,998
7
x
5
31,87 17
45x +
4,97 27
1 ++xxsin
0,007
8
xx
2
3++
1,97 18
1
21
2
xx++
1,006 28
3
3
xx+ cos
0,005
9 x
11
1,008 19
13 1
3
x -
4,97 29
2
2
4
x
x
- sin
π
1,003
10
38
3
x -
2,97 20
1
x
8,97 30
x
2
5+
1,995
112
Контрольные вопросы к заданиям 1–4
1. Как определяется производная? Ее физический, геометри-
ческий смысл.
2. Каковы правила дифференцирования? Производные основ-
ных элементарных функций.
3. Как определяется дифференциал? Каковы его свойства и
применение в приближенных вычислениях?
Задание 5. L:
xxt
yyt
=
=
(),
().
Найти уравнение касательной в точке со
значением t = t
0
, если х(t), y(t), t
0
, определяются по таблице:
n x(t) y(t) t
0
n x(t) y(t) t
0
n x(t) y(t) t
0
1 asin3t acos
3
t π/3 11 atcost at sint π/2 21
t -
-tsint
tcost 0
2
3
⋅ cost
sint π/3 12 sin
2
t cos
2
t π/6 22 1/t
2
1 :
:(t
2
+1)
1
3 a(t-sint)
a ×
× (1-cost)
π/3 13
arcsin
t
t1
2
+
arccos
t
t1
2
+
1 23 3cos t 4sint π/4
4 2t - t
2
3t - t
3
1 14
tt
t
+ ln
2
32+ lnt
t
1 24 t - t
4
t
2
- t
3
1
5
cost +
+ sint
sin2t π/4 15
1
2
+ t
t
3
2
2
2
t
t
+
2 25 t
3
+ 1
t
2
+
+ t + 1
1
6
arcsin
t
t1
2
+
arccos
t
t1 +
-1 16 asin
4
t acos
4
t π/6 26 2cost sint π/3
7
t(tcost -
- 2sint)
t(tsint +
+ 2cost)
π/4 17
a(tsint +
+ cost)
a(sint -
- tcost)
π/4 27 2tgt
2sin
2
t +
+ sin2t
π/4
8
3
1
2
at
t+
3
1
2
2
at
t+
2 18
t
t
+ 1
t
t
- 1
-1 28 t
3
+1 t
2
-2
9
1 +
+ 2lnctgt
tgt +
+ ctgt
π/4 19 1 - t
2
t - t
3
2 29 sint e
t
0
10
tt
24
24
-
tt
24
24
+
0 20 ln(1 + t
2
) t-arctgt 1 30 sin t cos2t π/6
Задание 6. Найти производную m-го порядка от функции
y = f
µ
(x), если σ, a, b берутся из задания 1, λ — из задания 2, µ — из
задания 3, f
µ
(x) — из таблицы:

113
µ
1 2 3 4 5 6
f
µ
(x) sinax
e
ax b+
σ
log( )
a
xb+
xa
xb
+
+
1
ax b+
λ
ax b+
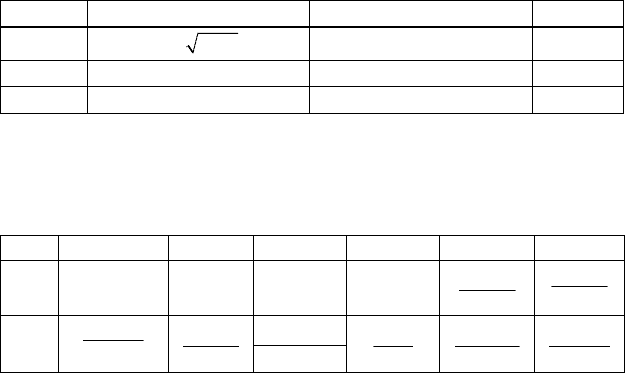
Задание 7. Применяя правило Лопиталя, найти
lim
()
()
,
xa
x
x
→
ϕ
ψ
если:
n ϕ(x) ψ(x) a
1 x - arctgx x
3
0
2 π - 2 arctgx ln(1 + 1/x)
∞
3 x - sinx x - tgx 0
4 π - 2 arctgx ln(x/(x + 1))
∞
5 π - 2arcsinx sin3(x - 1) 1
6 e
x
- e
-x
sinx cosx 0
7 1 - sin(πx/2) lnx 1
8 sin(πx/2) ln(1 - x) 0
9 xlnx - x + 1 (x - 1)lnx 1
10 a
2
- x
2
ctg(πx/(2a)) a
11
e
x
2
1-
cosx - 1 0
12 ln(sin2x) ln(sinx) 0
13 xcosx - xsinx x sinx 0
14
e
α x
- 1
sinβx
0
15 a
x
- b
x
xx1
2
-
0
16 1 - cos2x cos7x - cos3x 0
17 lnx 1 + 2ln(sinx) +0
18 e
3x
- 3x - 1 sin
2
5x 0
19 cosxln(x - 3) ln(e
x
- e
3
) 3 + 0
20 tg(πx/2) ln(1 - x) 1 - 0
21 e
x
- e
-x
- 2x x - sin x 0
22 e
2x
- 1 arcsinx 0
23 e
x
- 1 - x x(e
x
- 1) 0
24 (x - 2π)
2
tg(cosx - 1) 2π
25 cosx
(sin )1
2
3
- x
π/2
26 1 - sinx (π/2 - x)
2
π/2
27 tgx - x sinx - x 0
114
n ϕ(x) ψ(x) a
28
1 - cos x
sinx 0
29 lnx x
a
∞
30 ln(1 + x
2
) ln(π/2 - arctgx)
∞
Задание 8. Исследовать функции y = Ф
µ
(x), y = F
µ
(x) и постро-
ить их графики, если а берется из задания 1, r, µ — из задания 3;
Ф
µ
(x), F
µ
(x) — из таблицы:
µ
1 2 3 4 5 6
Ф
µ
(x)
(x - a)
2
(x - r)
ax
2
(x - r)
2
ax
2
(x
2
- r
2
) ax(x
2
- r
2
)
ax
xr
2
22
+
ax
xr
22
+
F
µ
(x)
ax r
xa
+
+()
2
ax
xr
2
22
-
()
()
xr a
ax r
++
+
22
ax
rx
3
-
xr
ax
33
2+
()xa
xr
+
-
2
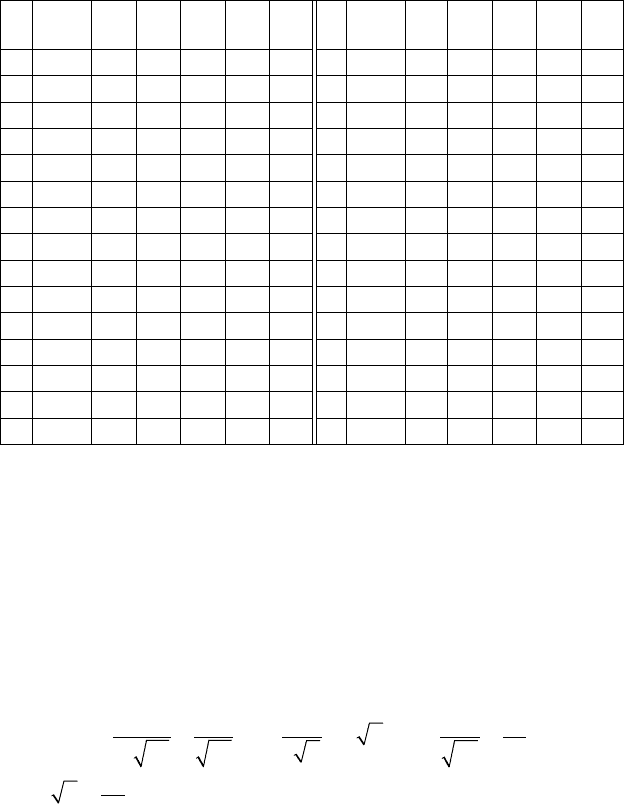
Задание 9. Решить задачу на экстремум.
1. Два тела движутся с постоянными скоростями v
1
(км/ч) и
v
2
(км/ч) по двум прямым, образующим угол π/2 в направлении к
вершине этого угла. В начале движения первое тело находилось от
вершины на расстоянии а (км), второе — на расстоянии b (км).
Через сколько минут после начала движения расстояние между
телами будет наименьшим?
2. Требуется изготовить закрытый цилиндрический бак вмес-
тимостью V (м
3
). Каковы должны быть размеры бака (радиус R и
высота H), чтобы на его изготовление пошло наименьшее количе-
ство материала?
3. Окно имеет форму прямоугольника с полукругом сверху.
Периметр окна равен а (м). Каковы должны быть его размеры
(ширина и высота), чтобы окно пропускало наибольшее количе-
ство света?
4. Требуется изготовить прямоугольный сосуд из прямоуголь-
ника со сторонами а (см) и b (см), вырезав углы и загнув края,
причем объем сосуда должен быть максимальным.
5. Требуется обтесать бревно с круглым сечением диамет-
ром а (см), чтобы получилась балка с прямоугольным сечением
наибольшей прочности. (В сопротивлении материалов установлено,
что прочность прямоугольной балки пропорциональна bh
2
, где b —
основание прямоугольника в сечении балки, h — его высота.)
115
6. Лодка находится на расстоянии а (км) от ближайшей точки
А берега. Пассажир лодки должен попасть в точку В на берегу, на-
ходящуюся на расстоянии b (км) от точки А. Известны скорость
лодки v
1
(км/ч), скорость пассажира v
2
(км/ч). К какому пункту на
берегу должна прибыть лодка, чтобы пассажир добрался до точки
В за кратчайшее время?
n
№
задачи
a b v
1
v
2
V n
№
задачи
a b v
1
v
2
V
1 1 20 30 50 60 16 4 70 40
2 2 8 17 5 21
3 3 14 18 6 2 4 5 6
4 4 40 30 19 1 50 40 30 20
5 5 30 20 2 32
6 6 3 5 4 5 21 3 17,5
7 1 40 20 10 30 22 4 50 32
8 2 16 23 5 24
9 3 10,5 24 6 3 6 3 5
10 4 50 18 25 1 40 50 10 40
11 5 27 26 2 64
12 6 4 5 3 6 27 3 42
13 1 30 20 40 60 28 4 70 55
14 2 4 29 5 33
15 3 7 30 6 2 3 4 6
Контрольные вопросы к заданиям 6–9
1. Как определяются производные и дифференциалы высших
порядков?
2. Запишите правило Лопиталя. Когда оно применяется?
3. Как производится исследование функций?
ответы к разд. 9, 10
9. Дифференцируемые функции одной переменной
1)
6
1
10
2
2
35
3
x
xx
+-;
2)
5
2
4
3
x
x+ ;
3)
22
7376
1
2
3
3
3
2
x
x
xx
x
+
-+ -
() ;
22
7376
1
2
3
3
3
2
x
x
xx
x
+
-+ -
() ;
4) - 5; 5) 1; 6) π /4 + 1/2;
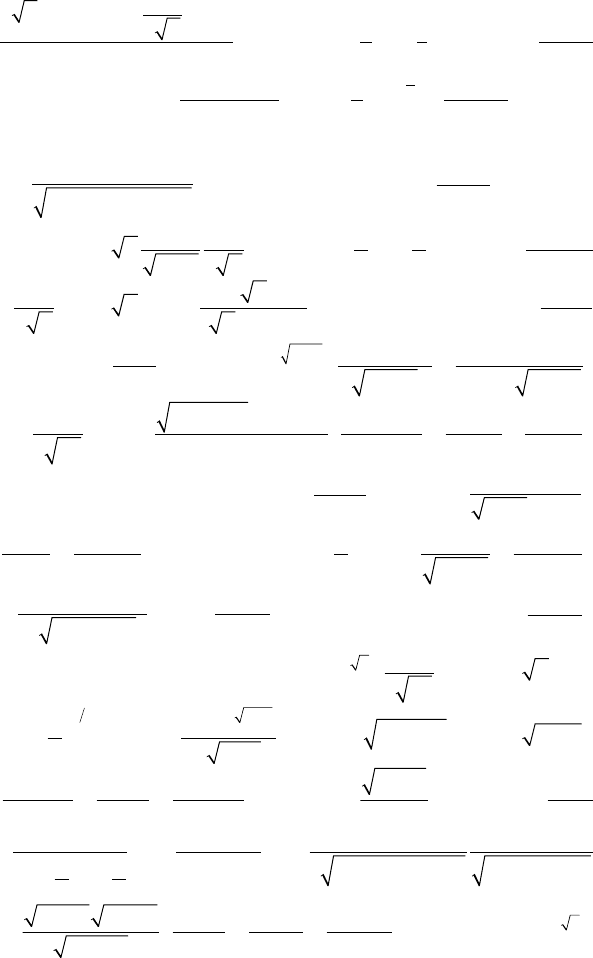
116
7)
2
1
2
2
xxx
x
x
x
sincos sin
;
-
8) 0; 2e
2
; 9)
-
1
4
;
10)
1
3
2
9
4
sin( )
cos
sin
;ee
xx
x
x
-
11)
-+5
2
452
5
xxx
xx
x
sinln
cosln
;
12)
6
5
1
2
5
2
22
xx
x
tg
cos
;
-
13) 0;
14)
2
2
x
x
e ;
15)
10 15 10
15 2
3
-
-
x
x()ln ;
16)
525
2
sin
sinln;
x
x
17) 0;
18)
x
xx()arcsin
;
1
42
-
19)
xx
x
x
xarctgarctg ;
4
2
5
1
2
+
+
20)
-
-
5
1
1
1
2
4
arccos;x
xx
21)
ππ
44
2
- ;
22)
ln
ln
;
x
x
- 2
3
23)
1
2
3
33
3
x
x
x
x
log( )
()ln
;++
+
24) 4ln
3
sinxctgx; 25)
12 5
5
ln
;
26)
xx
x
x
x +
+
+
1
1
ln ;
27)
(arctg )
lnarctg
arctg
;x
xx
xxx
x
2
1
22
1
1
1
+
+
+
+
28)
-
1
3
4
3
π
;
29)
()()
()
()
;
6545
27
9
26 5
8
45
6
27
3
4
2
3
xx
x
xxx
+-
+
+
+
-
-
+
30) 0; 31)
xxx
x
x
xsin
cosln
sin
;
2
22
2
+
32)
ln
sin
ln ()
ctg;
3
12
31
21
22
x
xx
xx x
x
-
×-
-
-
ln
sin
ln ()
ctg;
3
12
31
21
22
x
xx
xx x
x
-
×-
-
-
33)
-
-
+
1
1
2
x
x
x
x
x
xarcsin
ln arcsin
;
34)
21
3
3
(cos )
sin
;
-
-
ee
e
xx
x
x
35)
-33
25
ln
;
36) 8,5; 37)
e
1
2
1
+
+
tg
cos
;
x
x
x
38) 2sin1 + cos1 + 1/ln3; 39)
(cos )lncos tg ;x
x
xxx
x
3
1
3
2
3
3
-
40)
-
4
73
π
;
41)
cos
sin
;
sin
x
x
x
e
2
42)
()()
() ()
;xx x
x
x
x
x
+--×
+
+
-
+
-
214
2
52
6
1
1
24
2
5
23
2
()()
() ()
;xx x
x
x
x
x
+--×
+
+
-
+
-
214
2
52
6
1
1
24
2
5
23
2
43)
e
x
-1
2
;
44)
-
1
cos
;
x
45)
1
4
83
3
sincos
;
xx
46)
sin( tg )
cos
;
2
2
x
x
47)
1
321
2
12 1
2
3
2
(arcsin) ()
;
xx+-+
48)
3121
15 1
1
31
1
21
3
15 4
3
5
xx
x
xx x
-+
+
-
+
+
-
-
;
49)
(sin )
lnsin
ctg;x
x
x
xx
x
×+
2
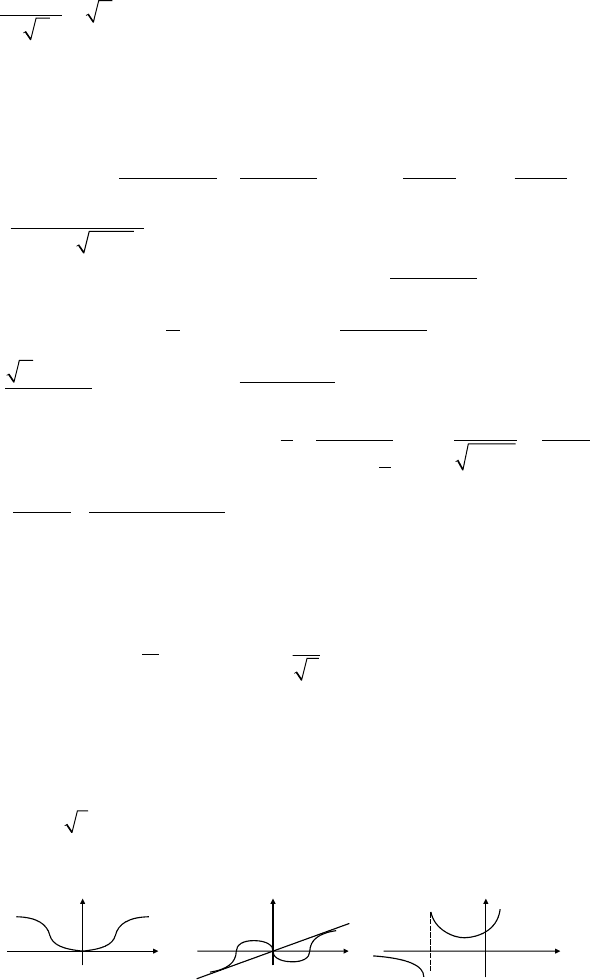
117
(sin )
lnsin
ctg;x
x
x
xx
x
×+
2
53) y = -2x + 1 — касательная; y = x/2 -
- 3/2 — нормаль; 54) 4x + 25y - 13 = 0 — касательная; 125x - 20y -
- 246 = 0 — нормаль; 55) y = x/4 + 2 — касательная; y = 296 -
- 4x — нормаль; 56) v(1) = 4 м/с; 57) 3 с; 58) 8 Дж; 59) 23A;
60) 3(1 + x - x
2
)
2
(1 - 2x)dx ; 61) 5
lnsinx
ctgx ln5dx ;
62)
()
ln()
cos
tg
;
tg
x
x
x
xx
x
x
x32
3
2
2
3
1
21
2
32
1
+
+
+
+
d
63)
6
1
2
1
2
2
2
+-x
x
x
xarctg;d
64)
2
2
cossin
coscos
;
xx x
xx
x
+
d
65) 2,008; 66) 0,849; 67) 0,5005; 68) 1,0035;
69)
223
2
2
xx
x
e
-
-();
70) 360; 71) 9; 72)
21
2
(ln)
;
- x
x
73) 3
n
e
3x
;
74)
-+
-
22
2
1n
xncos;
π
75)
dd
2
22
2
54
19
y
x
x
x=-
+()
;
76) d
2
y =
dd
2
3
2
3
4
y
xx
x
x=-
-()
;
77)
dd
2
3
2
21
1
y
x
x
x=
+
+
sin( )
cos( )
;
79) x ′ = t
2
- 4t + 3;
x″ = 2t - 4; t
1
= 1; t
2
= 3; 80)
ctg;
sin
;
t
a
t
2
1
4
2
4
-
81)
-
-
2
1
2
t
t
;
-
-
2
1
2
t
;
82)
1
1
+
-
tg
tg
;
t
t
2
3
e
t
tt(cos sin)
;
-
83) y - x ln2 - 1 = 0; y ln2 + x -
- ln2 = 0.
10. исследование функций и построение графиков
1) 1; 2) -π; 3)
m
n
a
mn-
;
4) 2; 5)
a
b
;
6) 0; 7) 0; 8) 0; 9) 1; 10) ∞;
11) а; 12) 0; 13) -2; 14) 1/6; 15) 0; 16) 1; 17) 1; 18) e
3
; 19) 1;
20) e
-1/2
; 21) y
min
= y(0) = 0; 22) y
max
= y(2kπ) = 0;
23) y
max
= y(1) = 1/2; y
min
= y(-1) = -1/2; 24) y
max
= y(1) = 1/e;
25) y
т.п
= y(b) = a; 26) т.п. нет; 27) y
1 т.п
= y(-1) = 2;
y
2 т.п
= y(1) = -2; 28) y
т.п
= y(2) = 0; 29) x = 0, y = 0, y = -1;
30) x = ±
3
; x + y = 0;
31) графики:
2) 3а) 3б)
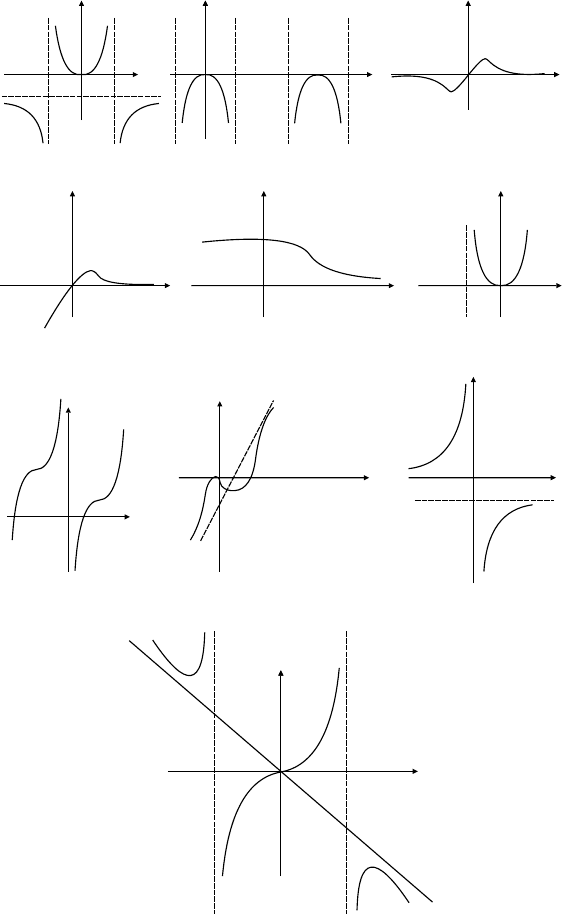
21) 22) 23)
24) 25) 26)
27) 28) 29)
30)
32) 12 ед. скорости; 33) 3; 34) H = R.

119
Глава 4
диФФеренциальное исчисление
Функций нескольких Переменных
11. диФФеренцируемые Функции
нескольких Переменных
опорный конспект № 11
11.1. Понятие функции нескольких переменных.
Элементы топологии в R
n
O: R
n
= {(x
1
,
x
2
,
...,
x
n
): x
i
∈ R, i =
1, n
}
y = f(x
1
,
x
2
, ..., x
n
), (x
1
,
x
2
, ..., x
n
) ∈ D ⊂ R
n
, y ∈ Y ⊂ R ⇔
⇔ D →: Y: ∀(x
1
, x
2
, ..., x
n
) ∈ D ∃! y ∈ Y ⊂ R
z = f(x, y), (x, y) ∈ D ⊂ R
2
— функция двух переменных;
f(x, y) = c, c = const — линии уровня
О: U
δ
(M
0
) = {M ∈ R
2
: |
MM
0
| < δ} — δ-окрестность т. M
0
(x
0
, y
0
)
D — открытая область ⇔ ∀M ∈ D ∃δ > 0: U
δ
(M) ⊂ D
11.2. Предел и непрерывность функций нескольких переменных
О: A =
lim(,)
MM
fxy
→
0
⇔ ∀e > 0 ∃ δ(e): M ∈ U
δ
(M
0
) ⇒
⇒ | f(x, y) - A| < e
О: z = f(x, y) непрерывна в т. М
0
(x
0
, y
0
) ⇔
1) f(x, y) определена в U
δ
(M
0
); 2)
lim(,)
MM
fxy
→
0
= f(x
0
, y
0
)
11.3. Частные приращения и частные производные
На примере z = f(x, y):
О: ∆
x
z = f(x + ∆x, y) - f(x, y), ∆
y
z = f(x, y + ∆y) - f(x, y) —
частные приращения по x и y
О:
∂
∂
=
→
z
x
z
x
x
x
lim,
∆
∆
∆
0
∂
∂
=
→
z
y
z
y
y
y
lim
∆
∆
∆
0
— частные производные
по x и y
11.4. Полное приращение и полный дифференциал,
применение в приближенных вычислениях
О: ∆z = f(x + ∆x, y + ∆y) - f(x, y) — полное приращение
функции z = f(x, y)
120
О: z = f (x, y) дифференцируема в т. M(x, y) ⇔ ∆z =
= A∆x + B∆y + ω(∆x, ∆y), ω = o(∆r) при
∆∆∆r= +→() () ,xy
22
0
dz
=
∂
∂
+
∂
∂
z
x
x
z
y
ydd
— полный дифференциал (dx = ∆x,
dy = ∆y).
f(x + ∆x, y + ∆y) ≈ f(x, y) +
∂
∂
+
∂
∂
f
x
x
f
y
y∆∆
— применение диф-
ференциала к приближенным вычислениям
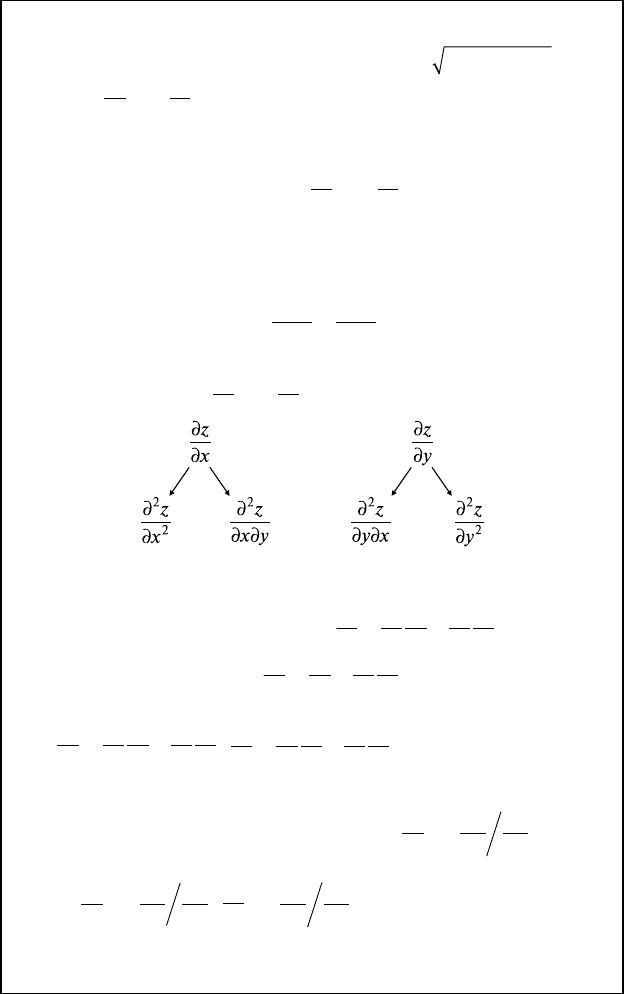
11.5. Частные производные и полные дифференциалы
высших порядков
В случае непрерывности
∂
∂∂
=
∂
∂∂
22
z
xy
z
yx
d
2
z = d(dz) — дифференциал 2-го порядка,
d
n
z = d(d
n-1
z) =
∂
∂
+
∂
∂
x
x
x
yz
n
dd.
11.6. Производные сложных функций
1) z = f(x, y), x = x(t), y = y(t):
d
d
d
d
d
d
z
t
z
x
x
t
z
y
y
t
=
∂
∂
+
∂
∂
;
2) z = f(x, y), y = y(x):
d
d
d
d
z
x
z
x
z
y
y
x
=
∂
∂
+
∂
∂
;
3) z = f(x, y), x = x(u, v); y = y(u, v):
d
d
z
u
z
x
x
u
z
y
y
u
=
∂
∂
∂
∂
+
∂
∂
∂
∂
,
d
d
z
v
z
x
x
v
z
y
y
v
=
∂
∂
∂
∂
+
∂
∂
∂
∂
11.7. неявные функции, их дифференцирование
1. F(x, y) = 0 задает неявно y = y(x) ⇒
d
d
y
x
F
x
F
y
=-
∂
∂
∂
∂
2. F(x, y, z) = 0 задает неявно z = z(x, y) ⇒
⇒
∂
∂
=-
∂
∂
∂
∂
z
x
F
x
F
z
,
∂
∂
=-
∂
∂
∂
∂
z
y
F
y
F
z
