Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Нуриева С.Н., Дегтярева О.М. Математика в примерах и задачах
Подождите немного. Документ загружается.


131
∂
∂
=
∂
∂
+
∂
∂
=
∂
∂
=
∂
∂
+
∂
∂
=
∂
∂
==
F
F
F
x
f
x
F
x
y
f
y
F
y
Fxy
λ
λ
λ
0
0
0
,
,
(, ),
()1
где Ф(х, у, λ) = f(x, y) + λF(x, y) — функция Лагранжа, λ ∈ R
Достаточные условия условного экстремума:
∆FF
0
00
00000
0
0
=-
′′
′′′′′
′′
FM FM
FM MM
FM
xy
xxxyx
y
() ()
() (,)(,)
()
λλ
′′ ′′
=
=
<⇒
>⇒
FF
yx yy
MM
M
M
(,)(,)
.max,
.
00 00
0
0
0
0
λλ
тт. усл.
тт. ус
—
— лл. min
М
0
(x
0
, y
0
), λ
0
— любое из решений (1)
12.3.Уравнения касательной плоскости и нормали к поверхности.
Линии как пересечение двух поверхностей
F(x, y, z) = 0 в т. М
0
(x
0
, y
0
, z
0
):
∂
∂
-+
∂
∂
-+
∂
∂
-=
F
x
xx
F
y
yy
F
z
zz
M
M
M
0
0
0
000
0() () ()
—
уравнение касательной плоскости
xx
F
x
yy
F
y
zz
F
z
M
M
M
-
∂
∂
=
-
∂
∂
=
-
∂
∂
000
0
0
0
— уравнение нормали
L
Fxyz
Fxyz
:
1
2
0
0
(, ,) ,
(, ,)
=
=
— линия пересечения двух поверхностей
SN N
ijk
F
x
F
y
F
z
F
x
F
y
F
z
M
=×=
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
12
111
222
0
— направляющий вектор
касательной к L
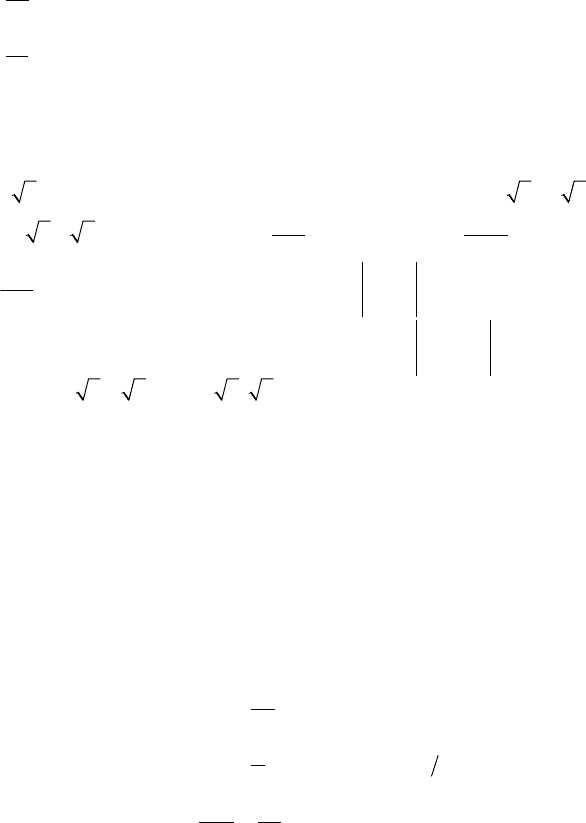
132
Задачи к разд. 12
Задача 1. Исследовать на экстремум функцию z = x
4
+ y
4
-
- 2x
2
+ 4xy - 2y
2
.
Решение: Область определения функции R
2
. Находим стацио-
нарные точки:
∂
∂
=-+=
∂
∂
=-+=
z
x
xxy
z
y
yyx
4440
4440
3
3
,
.
Получаем систему
xxy
yxy
xyxy
3
3
33
0
0
-+=
+-=
⇒=-⇒=-
,
,
.
Под-
ставляем у = -х в первое уравнение: x
3
- 2x = 0 ⇒ x
1
= 0, x
2,3
=
= ±
2
. Имеем три стационарные точки О(0, 0), М
1
(
2
, -
2
),
М
2
(-
2
,
2
). Находим
A
z
x
x=
∂
∂
=-
2
2
2
12 4,
B
z
xy
=
∂
∂∂
=
2
4,
C =
=
∂
∂
=-
2
2
2
12 4
z
y
y
и вычисляем
∆()M
AB
BC
=
(ОК, разд. 12.1):
∆(O) = 0 — сомнительный случай;
∆() ,
,
M
12
20 4
420
0=>
AM M
M
12
02222
12
,
(, ), (,)>⇒ --
AM M
M
12
02222
12
,
(, ), (,)>⇒ --
, — точки минимума, z
min
= 8.
В точке О(0, 0) проводим дополнительное исследование. Ис-
следуем знак приращения ∆z на линиях y = 0 и y = x. На у = 0
функция z = x
4
- 2x
2
имеет в точке О ∆z < 0. На у = х функция
z = 2x
4
имеет в точке О ∆z > 0. Таким образом, экстремума в точ-
ке О(0, 0) нет.
Задача 2. Найти условный экстремум функции z = x + 2y при
x
2
+ y
2
= 5.
Решение: Составляем функцию Лагранжа (ОК, разд. 12.2):
F(х, у, λ) = x + 2y + λ(x
2
+ y
2
- 5). Находим ∂F/∂х = 1 + 2λх,
∂F/∂λ = х
2
+ у
2
- 5, ∂F/∂y = 2 + 2λy и составляем систему
12 0
22 0
50
1
2
1
1
4
1
5
22
22
+=
+=
+-=
⇒
=-
=-
+=
λ
λ
λ
λ
λλ
x
y
xy
x
y
,
,
,
,
,
,
⇒=±=-
=- ==
λ
12 1
122
12 1
212
,
,,
,, .
x
yxy

133
y
1
= -2, x
2
= 1, y
2
= 2.
Итак, имеем две точки, подозрительные на условный экстре-
мум: М
1
(-1, -2) при λ = 1/2, М
2
(1, 2) при λ = -1/2. Находим
∂
2
F/∂х
2
= 2λ, ∂
2
F/∂х∂у = 0, ∂
2
F/∂у
2
= 2λ,
∂
∂
=+-
′
=
F
x
xy x
x
(),
22
52
∂
∂
=+-
′
=
F
y
xy y
y
()
22
52
и составляем (ОК, разд. 12.2)
∆FF
FF
=-
′′
′′′′′
′′′′′
0 FF
F
F
xy
xxxxy
yxyyy
,
т.е.
∆(,),M
11
024
21 0
40 1
0λ=-
--
-
-
>
∆(M
2
, λ
2
) =
∆(,).M
22
02 4
210
40 1
0λ=--
-
<
Функция имеет в точке М
1
условный min,
z
min
= -5, а в точке М
2
— условный max, z
max
= 5.
Задача 3. Определить, каковы должны быть размеры прямо-
угольного бассейна, чтобы при данной площади его поверхности S
объем бассейна был наибольшим.
Решение: Объем V = xyz, где х — длина, у — ширина, z — высо-
та бассейна. Так как задана площадь S = xy + 2zx + 2zy, то можно
выразить z через х, у и подставить в V: z = (S - xy)/(2x + 2y) ⇒
⇒ V = xy(S - xy)/(2x + 2y).
Ищем экстремум функции, учитывая, что x > 0, y > 0. Имеем
∂
∂
=
-
+
′
=
-+--
+
V
x
Sxyxy
xy
Sy xy xy Sxyxy
xy
x
22 222
2
2
2
()
()()()
(
))
() (
2
2223 22
2
2223
22
2
2
2
=
=
+- --+
+
=
--
+
SxySyxyxySxy xy
xy
Sy xy xy
xy
))
,
2
∂
∂
=
-
+
′
=
-+--
+
V
y
Sxyxy
xy
Sx yx xy Sxyxy
xy
y
22 222
2
2
2
()
()()()
(
))
()
.
2
2223
2
2
2
=
=
--
+
Sx xy yx
xy
Получаем систему
Sy xy xy
Sx xy yx
Sx xy
Sy yx
2223
2223
2
2
20
20
20
2
--=
--=
⇒
-- =
-- =
,
,
,
00
30
3
22 2
,
.
⇒
⇒=⇒=⇒- =⇒==xy xy Sx xy
S
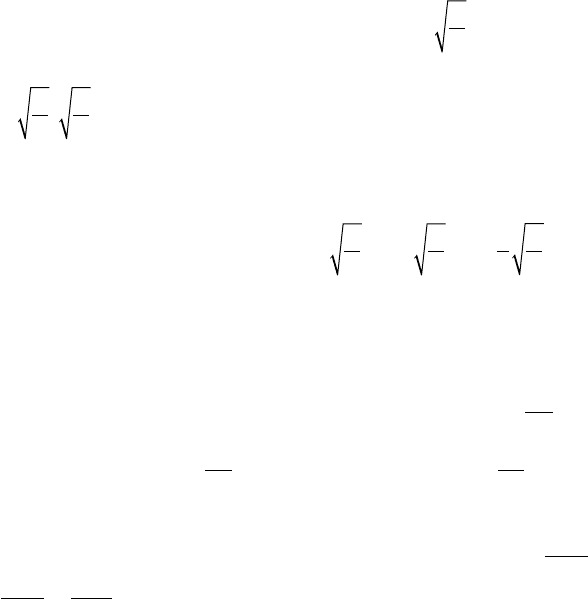
134
Sy xy xy
Sx xy yx
Sx xy
Sy yx
2223
2223
2
2
20
20
20
2
--=
--=
⇒
-- =
-- =
,
,
,
00
30
3
22 2
,
.
⇒
⇒=⇒=⇒- =⇒==xy xy Sx xy
S
Нашли одну стационарную точку в первом квадранте:
M
SS
33
,.
Так как функция V ≥ 0 для 0 ≤ xy ≤ S (V = 0 при
х = 0, у = 0, xy = S) и является непрерывной, то можно заклю-
чить, что в данной точке она имеет max. Данный вывод можно
проверить, используя достаточное условие экстремума (ОК,
разд. 12.1). Таким образом, при х =
S
3
,
у =
S
3
,
z =
1
23
S
,
объем
будет наибольшим.
Задача 4. Дана поверхность G: z = x
2
- 2xy + y
2
- x + 2y. Най-
ти уравнение касательной плоскости и нормали в точке
М
0
(1, 1, 1).
Решение: Имеем: F = x
2
- 2xy + y
2
- x + 2y - z,
∂
∂
=
F
x
M
0
=--=-(),2211
0
xy
M
∂
∂
=- ++ =
F
y
xy
M
M
0
0
2222(),
∂
∂
=-
F
z
M
0
1.
Уравнение касательной (ОК, разд. 12.3) -(х - 1) + 2(у - 1) -
- (z - 1) = 0 ⇒ x - 2y + z = 0; уравнение нормали
xyz-
-
=
-
=
-
-
1
1
1
2
1
1
.
xyz-
-
=
-
=
-
-
1
1
1
2
1
1
.
Задачи для самостоятельного решения
Исследовать на экстремум следующие функции:
1) z = 1 + 6x - x
2
- xy - y
2
; 2) z = x
2
+ y
2
- 2lnx - 12lny;
3) z = x
3
+ y
3
- 3xy.
Исследовать функции на условный экстремум:
4) z = 1 - 4x - 8y при x
2
- 8y
2
= 8; 5) z = xy при 2x + 3y -
- 5 = 0; 6) z = x
2
+ y
2
при x/4 + y/4 = 1.
7) Стоимость сооружения 1 м
2
стен фасада равна р, а 1 м
2
ос-
тальных стен — q, стоимость крыши за 1 м
2
ее основания — s. Ка-
ковы должны быть соотношения между длиной, шириной, высотой
для углового дома объемом V (м
3
), чтобы стоимость его стен и
крыши была минимальной?
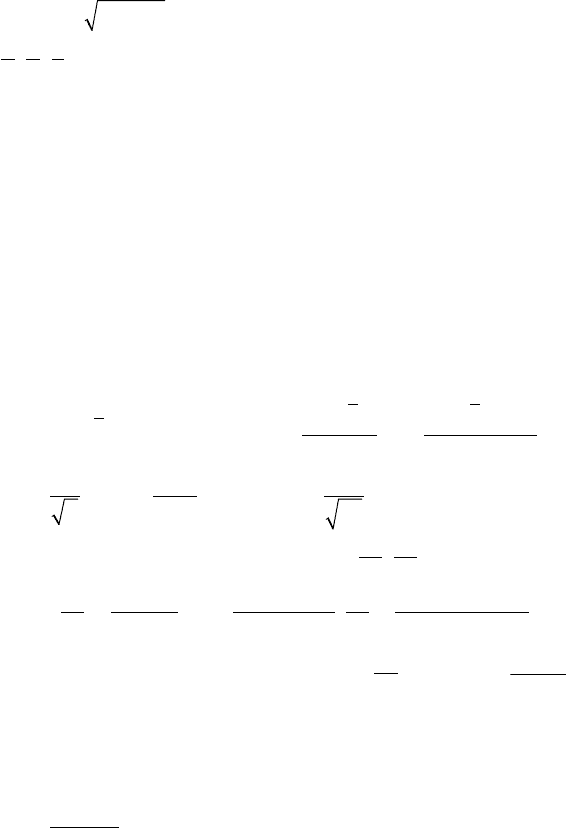
135
8) Палатка имеет форму цилиндра с насаженной на него кони-
ческой верхушкой. При каких соотношениях между линейными
размерами палатки для ее изготовления потребуется наименьшее
количество материала при заданном объеме V?
Для данных поверхностей найти уравнения касательных плос-
костей и нормалей в указанных точках:
9) G:
zxyxy=+-
22
,
M
0
(3; 4; -7); 10) G: z = sinx cosy,
M
0
44
1
2
ππ
;; ;
11) G: x
2
yz + 2x
2
z - 3xy + 2 = 0, M
0
(1; 0; -1).
Составить уравнение касательной прямой и нормальной плос-
кости для данных линий в указанных точках:
12)
L
yz
xy
:
22
22
25
10
+=
+=
,
,
M
0
(1; 3; 4); 13)
L
xyz
xyz
:
23 47
2
222
22
++=
+=
,
,
M
0
(-2; 1; 6).
Указание: В задачах 12), 13) воспользоваться формулой для на-
правляющего вектора
s
касательной прямой.
варианты контрольной работы
Вариант № 1
1.
zx
y
= (tg);
1
dz = ? Ответ:
dd dz
x
yx
x
xx
y
y
yy
=-
-
(tg)
cos
(tg)ln tg
.
1
1
2
1
2
2.
z
x
y
y
z
xy
=-
∂
∂∂
=
3
3
2
2
tg ;?
Ответ:
-
x
y
2
4
3
.
3. z = ln(x
3
+ 3y), x = utgv, y = 1/u
3
;
∂
∂
∂
∂
=
z
u
z
v
,?
Ответ:
∂
∂
=
+
-
+
∂
∂
=
+
z
u
x
xy
v
xyu
z
v
xu
xy v
3
3
9
3
3
3
2
334
2
32
tg
()
,
()cos
.
4. x
2
- x ⋅ 2
y+1
+ 4
y
- x + 2
y
+ 2 = 0;
d
d
y
x
= ?
Ответ:
1
22
y
ln
.
5. Найти экстремумы функции z = x
2
+ xy + y
2
- 3x - 6y.
Ответ: z
min
= z(0; 3) = -9.
Вариант № 2
1.
z
xy
xy
=
+
3
ln
;
dz = ?
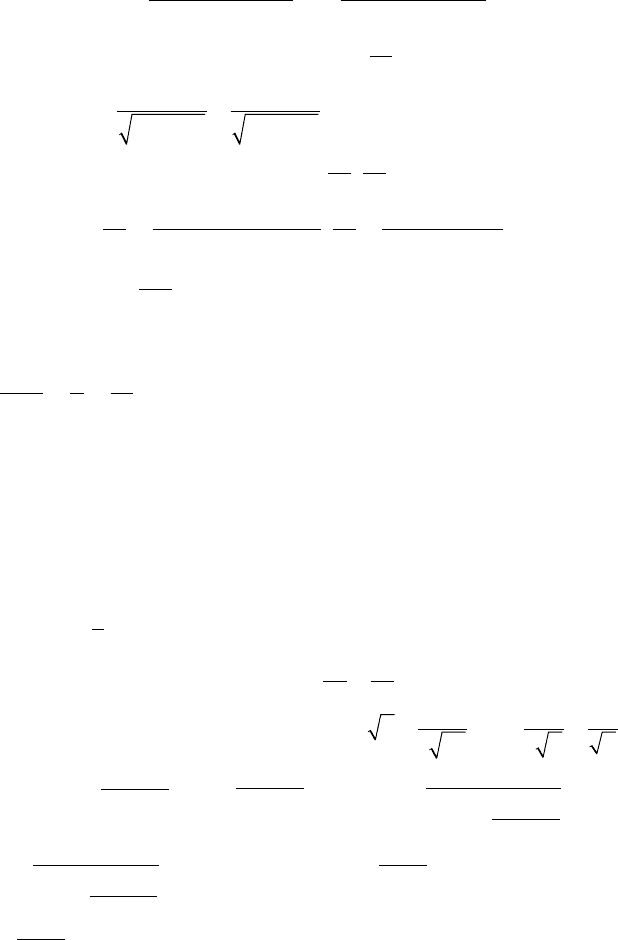
136
Ответ:
dddz
xy xy y
xy
x
xxxy
xy
y=
+
+
+
-+
+
23
22
2
433
2
ln
(ln)
ln
(ln)
.
2. z = arccosx
2
y, x = e
3t
, y = cos5t;
d
d
z
t
= ?
Ответ:
-
-
+
-
6
1
55
1
3
42
2
42
xy
xy
xt
xy
t
e sin
.
3. xsiny + ysinx + zsinx = z
3
;
∂
∂
∂
∂
=
z
x
z
y
,?
Ответ:
∂
∂
=
++
-
∂
∂
=
+
-
z
x
yyzx
zx
z
y
xy x
zx
sin( )cos
sin
,
cossin
sin
.
33
22
4. z = y
lnx
;
∂
∂
=
2
2
z
y
?
Ответ: lnx(lnx - 1)y
lnx-2
.
5. Найти касательную плоскость и нормаль к поверхности G:
z = ln(x
2
+ y
2
) в точке М
0
(1, 0, 0). Ответ: 2x - z - 2 = 0,
xyz-
==
-
1
201
.
Ответы к разд. 11, 12
11. Дифференцируемые функции нескольких переменных
1) D = {(x, y): x
2
+ 3y
2
≤ 3} (замкнутая ограниченная область);
2) D = {(x, y): y ≠ ±2х} (имеются две линии разрыва); 3) D =
= {(x, y): x ≥ 0,
y > 0}; 4) D = {(x, y): x + y > 0}; 5) D = {(x, y):
-1 ≤ x + y ≤ 1}; 6) D = {(x, y, z): x
2
+ y
2
< 2z}; 7) Окружности
xy
c
22
4
+=;
8) Прямые у = сх; 9) Гиперболы х
2
- у
2
= с; 10) Эл-
липтические параболоиды
zc
xy
=+ +
22
49
;
11) Гиперболоиды х
2
+
+ y
2
- z
2
= c; 12) 12; 13) 1/2; 14)
′
=-zy
y
x
x
3
4
3
;
′
=+z
x
yx
y
2
1
3
;
15)
′
=-
+
z
y
xy
x
22
;
′
=
+
z
x
xy
y
22
;
16)
′
=-
-
z
y
x
xy
x
x
2
22
2
3
cos
;
z ′
y
=
=-
-
2
3
2
2
y
x
xy
x
cos
;
17)
′
=++
+
zyxy
xy
xy
x
ln() ;
z ′
y
= x ln(x + y) +
+
+
xy
xy
;
18)
′
=+
-
zxxyx
x
xy
y
1
1(ln);
′
=zxxx
y
yx
y
ln ;
2
19) u ′
x
=
137
′
=
++
u
x
xyz
x
2
235
,
′
=
++
u
y
xyz
y
3
2
235
,
′
=
++
u
z
xyz
z
5
4
235
;
20) u ′
x
=
= yz(sinx)
yz-1
cosx; u′
y
= z(sinx)
yz
lnsinx; u′
z
= y(sinx)
yz
lnsinx; 21) u′
x
=
= y
2
z
3
t
4
+ 3; u′
y
= 2xyz
3
t
4
- 4; u′
z
= 3xy
2
z
2
t
4
+ 2; u′
t
= 4xy
2
z
3
t
3
+
+ 1; 22)
d
dd
z
xy xy yx
xy
=
-
-
4
222
()
()
;
23) du =
y
z
dx + (cos(y + 3z) +
+
x
z
)dy + (3cos(y + 3z) -
xy
z
2
)dz; 24) 0,005; 25) 8,29; 26) z ′′
xx
=
= 8cos(4x + 6y); z ′′
xy
= 12cos(4x + 6y); z ′′
yy
= 18cos(4x + 6y);
27)
′′
=-
+
z
y
xy
xx
4
3
()
;
′′
=
-
+
z
xy
xy
xy
2
3
()
()
;
′′
=
+
z
x
xy
yy
4
3
()
;
28) z ″
xx
=
′′
=
-
z
xy
xy
xx
3
223
1()
;
′′
=
-
z
xy
xy
1
1
223
()
;
′′
=
-
z
yx
xy
yy
3
223
1()
;
29) z ′′′
xxy
=
2y
3
(2 + xy
2
)
e
xy
2
;
30)
′′′
=u
z
xyz
1
2
;
33)
-+ -
+
yx xy xy xy
xxy
22 22
2
2
2
3
2
dddd
()
;
34) 2sin2y dx dy + 2x cos2y dy
2
; 35)
d
d
z
t
x
y
xt
xt
y
=+
ln cos;
36)
d
d
z
t
xy tyx
t
=+ ++()sin( )
cos
;222
1
2
37)
d
d
z
x
yx
yx
=
-+
++
(( ))
()
;
12 1
1
2
22
38)
∂
∂
=-+
-
z
u
u
v
uv
u
vu v
232
3
32
2
2
2
ln()
()
;
∂
∂
=
-
--
-
z
v
u
v
uv
u
vu v
2
32
2
32
2
3
2
2
ln()
()
;
∂
∂
=
-
--
-
z
v
u
v
uv
u
vu v
2
32
2
32
2
3
2
2
ln()
()
;
39)
∂
∂
=-
z
u
xy yv()cos;2
2
∂
∂
=- -+-
z
v
xy yu vx xy v()sin( )cos ;22
22
∂
∂
=- -+-
z
v
xy yu vx xy v()sin( )cos ;22
22
40)
∂
∂
=
u
t
-yz/x + z/(xt) + 2ty/x; 41) u ′
x
= 1 +
+ xt
2
(2 + 3xtv
3
); u′
t
= xt
2
(2 + 3xtv
3
); u′
v
= 3x
3
t
3
v
2
; 42)
-
x
y
;
43)
y
x
;
44)
yx
xy
2
2
1
1
(ln)
(ln)
;
-
-
45)
∂
∂
=
-
z
x
yz
xy
z
e
;
∂
∂
=
-
z
y
xz
xy
z
e
;
46)
∂
∂
=
+
z
x
z
y
1
1 ln
;
∂
∂
=
+
z
y
z
y
z
y
(ln)
;
1
47)
∂
∂
=
z
x
1;
∂
∂
=
-
-++
z
y
zx
zx yy()
.
22
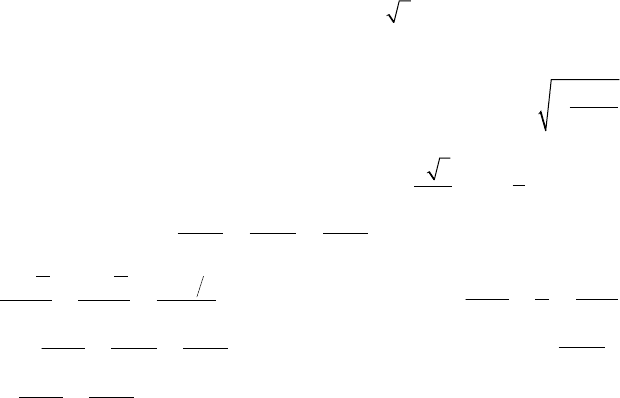
12. Приложения дифференциального исчисления
функций нескольких переменных
1) z
max
= z(4, -2) = 13; 2) z
min
= z(1,
6
) = 7 - 6ln6; 3) z
min
=
= z(1, 1) = -1; 4) z
max
= z(4, -1) = -7; z
min
= z(-4, 1) = 9;
5) z
max
= z(5/4, 5/6) = 25/24; 6) z
min
= z(36/25, 48/25) =
= 144/25; 7) Основание дома — квадрат со стороной
V
pq
s
+
3
;
8) R — радиус палатки, Н — высота цилиндрической части, h —
высота конической верхушки; тогда
R
h
=
5
2
,
H
h
=
2
;
9) 17х +
+ 11у + 5z = 60;
xyz-
=
-
=
+3
17
4
11
7
5
;
10) х - у - 2z + 1 = 0;
xy
z
-
=
-
-
=
-
-
ππ
4
1
4
1
12
2
;
11) 2х + 2у - z - 3 = 0;
xyz-
==
+
-
1
22
1
1
;
12)
xyz-
=
-
-
=
-1
12
3
4
4
3
;
12x - 4у + 3z - 12 = 0; 13)
xyz+
=
-
=
-2
27
1
28
6
4
;
xyz+
=
-
=
-2
27
1
28
6
4
;
27x + 28y + 4z + 2 = 0.
139
Глава 5
комПлексные числа.
Функции комПлексноГо ПеременноГо
13. комПлексные числа (к.ч.)
опорный конспект № 13
13.1.Алгебраическая форма к.ч.
z = x + iy, x, y ∈ R, i =
-1
, (i
2
= -1) —
мнимая единица, х = Re z, y = Imz — действи-
тельная и мнимая части
Равенство к.ч.: z
1
= z
2
⇔ Re z
1
= Re z
2
и
Im z
1
= Im z
2
z
= x - iy — комплексно-сопряженное к z
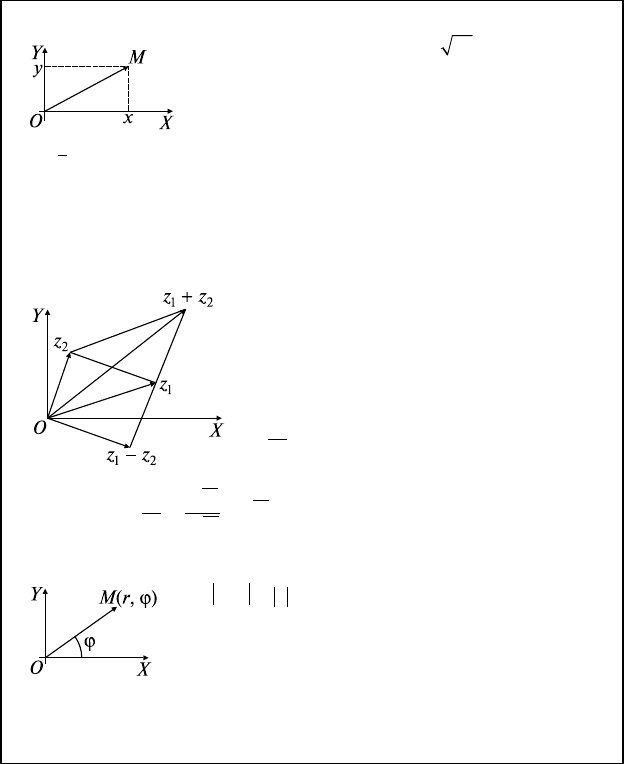
На комплексной плоскости:
z — точка М(х, y) или
OM
OX — действительная ось, OY — мнимая ось
13.2. Действие над к.ч. в алгебраической форме
z
1
= x
1
+ iy
1
, z
2
= x
2
+ iy
2
1) z
1
+ z
2
= (x
1
+ x
1
) + i(y
1
+ y
2
)
2) z
1
- z
2
= z ⇔ z + z
2
= z
1
3) z
1
z
2
= (x
1
x
2
- y
1
y
2
) + i(x
1
y
2
+ x
2
y
1
)
(по правилу умножения многочленов,
i
2
= -1)
4)
z
z
zzzz
1
2
21
=⇔ =
Правило:
z
z
zz
zz
zz xy
1
2
12
22
22 2
2
2
2
==+,
13.3. Тригонометрическая и показательная формы к.ч.
rOMz OX OM z====
,(,)Argϕ
Главное значение:
argz ∈ [0, 2π) или argz ∈ [-π, π) ⇒
Argz = argz + 2kπ, k = 0, ±1, ±2, ..., x =
= rcosϕ, y = rsin ϕ ⇒ z = r(cosϕ + i sinϕ),
сosϕ + isinϕ = e
iϕ
— формула Эйлера ⇒ z = re
iϕ
z
1
= z
2
⇔ |z
1
| = |z
2
|, Argz
1
= Argz
2
+ 2kπ
140
13.4. Умножение и деление в тригонометрической
и показательной формах
z
1
=
r
i
1
1
e
ϕ
= r
1
(cosϕ
1
+ isinϕ
1
), z
2
=
r
i
2
2
e
ϕ
1) z
1
z
2
= r
1
r
2
(cos(ϕ
1
+ ϕ
2
) + isin(ϕ
1
+ ϕ
2
)) = r
1
r
2
e
i()ϕϕ
12
+
2)
z
z
r
r
i
r
r
i
1
2
1
2
12 12
1
2
12
=-+-=
-
(cos()sin( ))
()
ϕϕ ϕϕ
ϕϕ
e
13.5. Возведение в степень n (n ∈ N) и извлечение корня
степени n из к.ч.
1)
zzzzrrnin
n
n
ninn
=⋅⋅⋅== +... (cos sin)
e
ϕ
ϕϕ
2)
zw wzwzrr
r
k
n
i
k
n
n
n
n
i
n
n
inkn
n
=⇔ ==== =
=
+
+
+
+
,
cossin
()
ee
ϕϕπ
ϕπ ϕπ
2
22
,
kn=-01,.
Задачи к разд. 13
Задача 1. Найти комплексные корни квадратного уравнения
z
2
- 4z + 5 = 0 и изобразить их на комплексной плоскости.
Решение: Используем формулу для корней квадратного уравне-
ния az
2
+ bz + с = 0, у которого ∆ = b
2
- 4ac < 0, т.е. в про-
странстве комплексных чисел
∆= -iacb4
2
.
Тогда
z
bi ac b
a
ii
i
12
2
4
2
42016
2
42
2
2
,
.=
±-
=
±-
=
±
=±
Строим комплексно-сопряженные числа z
1
= 2 + i, z
2
=
=
z
1
= 2 - i на комплексной плоскости (рис. 13.1).
Рис. 13.1
