Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Нуриева С.Н., Дегтярева О.М. Математика в примерах и задачах
Подождите немного. Документ загружается.


151
12)
dx
xa
xxac
22
22
±
=+±+
∫
ln ;
13)
dx
x
xc xc
2
1+
=+=- +
∫
arctgarcctg;
14)
dx
ax
x
a
c
22
-
=+
∫
arcsin ;
15)
dx
ax
a
x
a
c
22
1
+
=+
∫
arctg;
16)
dx
ax
a
ax
ax
c
22
1
2
-
=
+
-
+
∫
ln
15.4. Методы интегрирования
1. Метод разложения (3
0
, 4
0
)
2. Метод замены переменной
fx x
xt
xtt
ft tt()
(),
()
[()] ()
∫∫
=
=
=
′
=
′
d
dd
d
ϕ
ϕ
ϕϕ
3. Метод интегрирования по частям
∫udv = uv - ∫vdu.
Применяется для:
1)
Px
a
x
x
kx
() ,
∫
e
d
P(x) — многочлен,
Px
kx
kx
x()
sin
cos
,
∫
d
P(x) = u;
2)
Px xx Px
x
x
x
x
a
()log,()
arcsin
arccos
arctg
arcctg
d
∫∫
dx,
P(x)dx = dv;
3)
ed
ax
bx
bx
x
∫
sin
cos
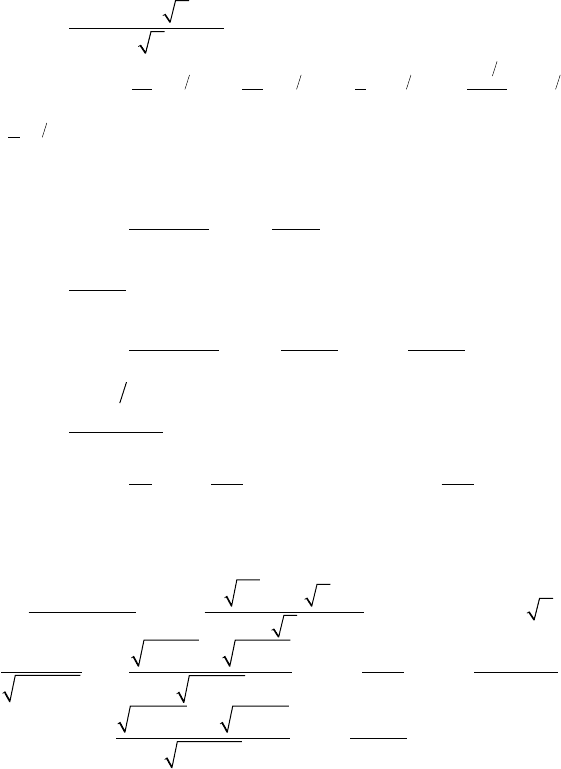
152
Задачи к разд. 15
1. Интегрирование методом разложения (непосредственное ин-
тегрирование)
Метод заключается в переходе от данного неопределенного
интеграла к табличным интегралам с помощью свойств 3
0
, 4
0
(ОК,
разд. 15.2).
Вычислить интегралы:
1.
J
xxx
x
x=
-+
∫
11 13 2
6
3
3
d .
Решение:
Jxxxxxx
x
x=-+=-+
∫∫∫
-
11
6
13
6
1
32
83 76 13
11 3
13 6
ddd
++
1
2
23
xc.
2.
Jxx=
∫
ctg.
2
d
Решение:
J
x
x
x
x
x
xxxc=
-
=-=- -+
∫∫∫
1
2
2
sin
sin
ctg.d
d
sin
d
2
3.
J
x
x
x=
+
∫
2
2
4
d .
Решение:
J
x
x
x
x
x
x
x
x
=
+-
+
=
+
+
-
+
=
∫∫∫
2
2
2
22
44
4
4
4
4
4
dd
d
=- +xxc22arctg( ).
4.
Jx
xx x
x
=
+
∫
23 12
6
d .
Решение:
Jx xx xx c
x
x
x
x
x
x
=+ =+ =+ +
∫∫ ∫
6
6
12
6
2
2
2
dd d
ln
.
Задачи для самостоятельного решения
1)
13 4
2
-+
∫
xx
x
xd ;
2)
13 74
4
5
4
xxx
x
x
-+
∫
d ;
3)
()();12-+
∫
xxxd
4)
dx
x73
2
-
∫
;
5)
xx
x
x
22
4
33
9
-- +
-
∫
d ;
6)
25
xx
x
x
e
d ;
∫
7)
12-
∫
cos
sin
;
x
x
xd
8)
tg ;
2
xx
∫
d
9)
434
16
22
4
+- -
-
∫
xx
x
;
10)
2
1
2
2
+
+
∫
x
x
xd .
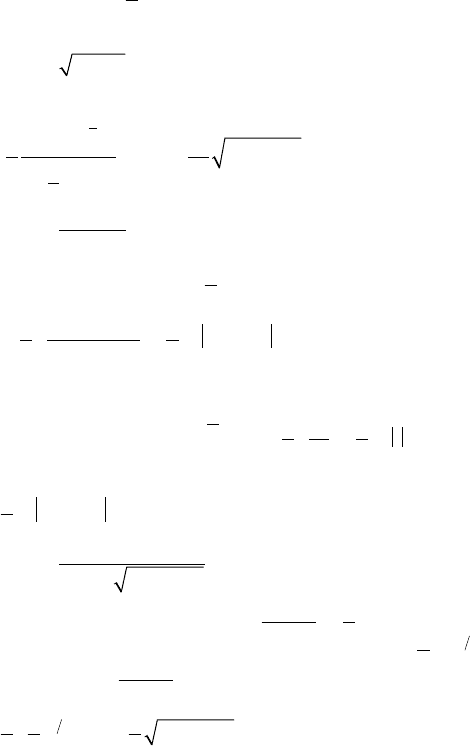
153
2. Интегрирование заменой переменных
Рассмотрим простейший случай метода замены переменной,
когда применима формула
fx xx
xt
xx xt
ft t[()] ()
() ,
() ()
() ,ϕϕ
ϕ
ϕϕ
∫∫
′
=
=
′
==
=d
dd d
d
(15.1)
причем интеграл справа является табличным. В этом случае метод
называется подведением под знак дифференциала. В частном слу-
чае, когда ϕ(x) = ax + b, пользуемся формулой
faxbx
a
Faxb c() ().+= ++
∫
d
1
(15.2)
Вычислить интегралы:
1.
Jxx=-
∫
12
5
d .
Решение: По формуле (15.2) получаем ax + b = -2х + 1, a = -2,
J
x
cxc=-
-
+
+=--+
+
1
2
12
1
5
1
5
12
12
1
5
1
6
5
()
().
2.
J
x
xa
x=
+
∫
22
d .
Решение: Так как
xx xadd=+
1
2
22
(),
то
J
xa
xa
xac=
+
+
=++
∫
1
2
1
2
22
22
22
d()
ln .
Или с помощью замены переменной по формуле (15.1):
J
xatxxt
xx t
t
t
tc
x
=
+= =
=
==+=
=
∫
22
1
2
2
1
2
1
2
1
2
,,
ln
ln
dd
dd
d
222
++ac.
3.
J
x
xx
=
+
∫
d
costg
.
2
3
32
Решение:
J
xt
x
x
t
x
xt
t=
+= =
=
=
-
∫
32
1
2
2
1
2
2
2
13
tg ,
cos
,
cos
d
d
dd
dtt =
=⋅ += ++
3
4
3
2
3
4
32
23
3
tc xctg .
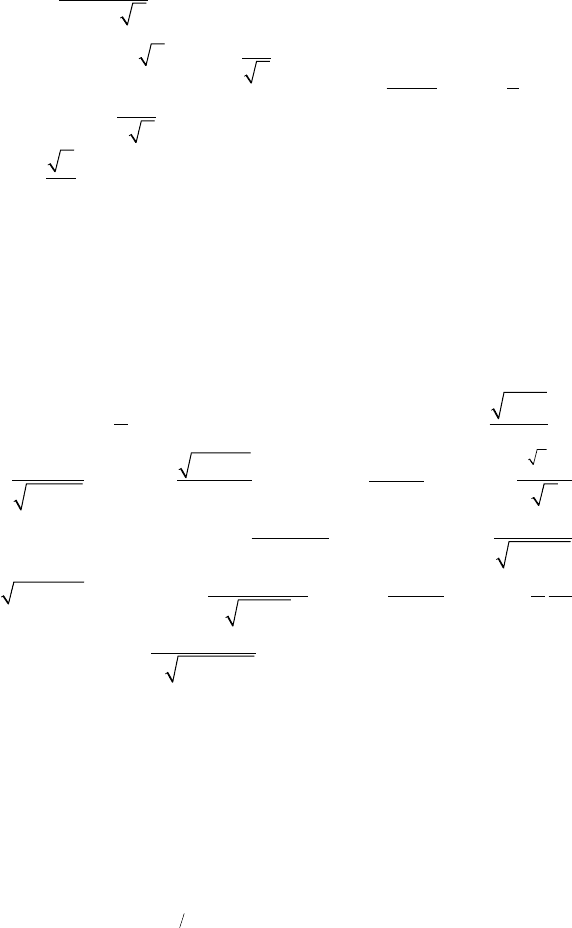
154
4.
J
x
xx
=
+
∫
d
()
.
4
Решение:
J
xt
x
x
t
x
xt
t
t
t
c=
==
=
=
+
=+=
∫
,,
arctg
d
d
dd
d
2
1
2
2
4
2
2
=+arctg.
x
c
2
5.
Jxx
x
=
∫
ed
cos
sin.
Решение:
J
xt xx t
xx t
=
==-
-=
=
cos,sin,
sin
dd
dd
=- =- +=-+
∫
ed ee
tt x
tc c
cos
.
Задачи для самостоятельного решения
11)
cos( );5
4
xx+
∫
π
d
12)
ed
-+
∫
23x
x;
13)
xx
x
ed
2
∫
;
14)
ln
;
3
4
x
x
xd
∫
15)
xx
x
d
4
2
-
∫
;
16)
arctg
;
x
x
x
3
2
1 +
∫
d
17)
dx
x35-
∫
;
18)
5
x
x
x
d
∫
;
19)
xxx
23
sin;
∫
d
20)
cos(ln )
;
x
x
xd
∫
21)
ed
e
x
x
x
2
5+
∫
;
22)
1 -
∫
sincos ;xxxd
23)
arcsin
;
x
x
x
-
-
∫
3
1
2
d
24)
xx
x
d
4
9+
∫
;
25)
cos;
1
2
x
x
x
d
∫
26)
ed
3
2
xx
x
+
∫
ln
;
27)
dx
xx4
2
-
∫
ln
.
3. Интегрирование по частям
Метод интегрирования по частям заключается в применении
формулы
uv uv vudd
∫∫
=-
(15.3)
в случаях, когда интеграл, записанный справа, проще для вычис-
ления, чем заданный. Наиболее важные случаи использования
формулы приведены в ОК, разд. 15.4.
Вычислить интегралы:
1.
Jxxx
x
=-+
∫
().
23
2e d
Решение: Имеем случай 1) из п. 3 ОК, разд. 15.4:

155
J
xx uuxx
xvvx
xxx
=
-+==-
===
=
=
∫
2
333
221
3
3
,(),
,
dd
ed dede
(()().2232 1
33
xx xx
xx
-+ --
∫
eed
После применения формулы интегрирования по частям степень
многочлена под знаком интеграла понизилась на единицу. Приме-
ним еще раз формулу (15.3), получим
J
xu ux
xvvx
xx
xxx
=
-= =
== =
=
=-+
∫
21 2
3
32
333
2
,,
,
(
dd
ed dede
))[() ]
()()
eeed
eee
xxx
xxx
xx
xx x
333
23 33
92 12
3292 154
---=
=-+--+ +
∫
cc.
2.
Jxx=
∫
arctg.4d
Решение: Имеем случай 2) из п. 3 ОК, разд. 15.4:
J
xu u
x
x
xv vxx
xx
=
==
+
===
=
=
∫
arctg, ,
,
arctg
4
4
116
4
2
dd
dd d
--
+
=
+=
=
=
=
=
∫
4
116
116
32
32
2
2
xx
x
xt
txx
xx t
x
d
dd
dd
,
,
arctg
44
4
32
1
8
4
1
8
116
2
x
t
t
xx tc
xx xc
-= -+=
=-++
∫
d
arctgln
arctgln( ).
3.
J
x
x
x=
∫
ln
.
5
d
Решение: Имеем случай 2) из п. 3 ОК, разд. 15.4:
J
xu
x
x
u
x
x
vv xx x
x=
==
== =
=
-
∫
ln ,,
,
d
d
d
dd
5
1
5
4
5
4
5
5
4
5
4
lln xx
x
x
-=
∫
5
4
4
5
d
=- =-+
-
∫
5
4
5
4
5
4
25
16
4
5
1
5
4
5
4
5
xx xx xx xcln ln .d
156
4.
Jxx
x
=
∫
ed
2
4cos.
Решение: Имеем случай 3) из п. 3 ОК, разд. 15.4:
Jxx
uux
xx vv xx
x
xx
==
==
== =
∫
∫
ed
eded
dd d
2
22
4
2
44
1
4
4
cos
,,
cos,cossin
xx
xxx
xx
=
=-
∫
1
4
4
1
2
4
22
sinsin .ee d
Применяя еще раз формулу (15.3), придем к первоначальному
интегралу.
J
uux
xx vv xx x
xx
=
==
== =-
∫
eded
dd d
22
2
44
1
4
4
,,
sin,sincos
==
=--+
∫
1
4
4
1
2
1
4
4
1
2
4
222
sincos cos,xxxx
xxx
eeed
Jx xxx
xxx
=+-
∫
1
4
4
1
8
4
1
4
4
222
sincos cos.eeed
Получили уравнение с неизвестной величиной J:
Jx xJ
xx
=+-
1
4
4
1
8
4
1
4
22
sincos ,ee
откуда
Jx xc
xx
=+ +
1
5
4
1
10
4
22
sincos .ee
Задачи для самостоятельного решения
28)
x
x
x
3
14-
⋅
∫
d ;
29)
xxx
∫
ln ;
2
d
30)
arcsin ;2xxd
∫
31)
xxx
2
2
∫
sin;d
32)
ed
2
3
x
x
x
∫
sin;
33)
arctg;xxd
∫
34)
xx
x2
ed
-
∫
;
35)
arctg
;
e
e
d
x
x
x
∫
36)
()ln();xxxx
2
1++
∫
d
37)
xxxtg ;
2
d
∫
38)
ln();1
2
+
∫
xxd
39)
xx
x3
2
ed
-
∫
;
40)
cos(ln ).xxd
∫
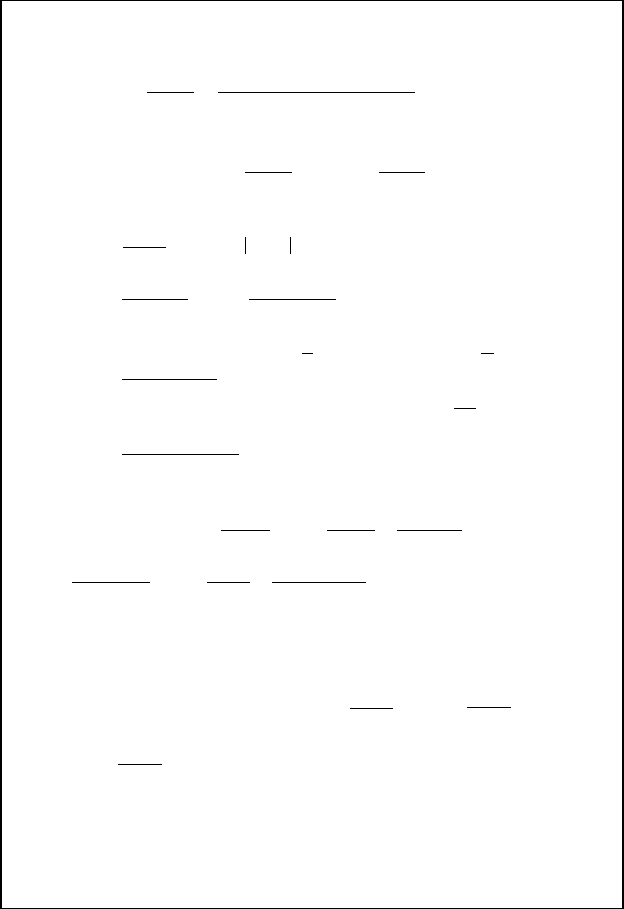
157
16. классы интеГрируемых Функций
опорный конспект № 16
16.1. интегрирование рациональных дробей
O:
Rx
Px
Qx
Bx Bx B
Ax Ax A
m
n
mm
m
nn
n
()
()
()
...
...
==
+++
+++
⇒
-
-
01
1
01
1
неправвильная
если
правильная
если
,
,
mn
mn
≥
<
Неправильная
Rx
Px
Qx
Lx
rx
Qx
m
n
l
k
n
()
()
()
()
()
()
,==+
k < n
Правильная R(x) = ∑ простейших дробей 1–4 типов:
1 тип:
A
xa
xAxa c
-
=-+
∫
d ln ,
2 тип:
A
xa
xA
xa
k
c
k
k
()
()
,
-
=
-
-+
+
∫
-+
d
1
1
3 тип:
Mx N
xpxq
x
txpx qx
p
xpxqtq
p
+
++
=
=++
′
=+
++=+-
∫
2
2
22
2
1
22
4
d
()
,
4 тип:
Mx N
xpxq
x
k
+
++
∫
()
.
2
d
Пусть Q
n
(x) = (x - a
1
) ... (x - a
l
)(x - b)
k
(x
2
+ px + q) ⇒
правильная
Rx
A
xa
A
xa
B
xb
l
l
k
k
() ...
()
=
-
++
-
+
-
+
1
1
+
-
++
-
+
+
++
-
-
B
xb
B
xb
Mx N
xpxq
k
k
1
1
1
2
()
...
16.2. интегрирование тригонометрических функций
1. ∫R(sinx, cosx)dx = ∫R*(t)dt,
если tg(x/2) = t, x = 2arctgt,
d
d
x
t
t
=
+
2
1
2
,
sin,x
t
t
=
+
2
1
2
cos.x
t
t
=
-
+
1
1
2
2
2. ∫sin
m
xcos
n
xdx, m, n ≥ 0, целые
а) m = 2p + 1 ⇒ cosx = t
n = 2q + 1 ⇒ sinx = t
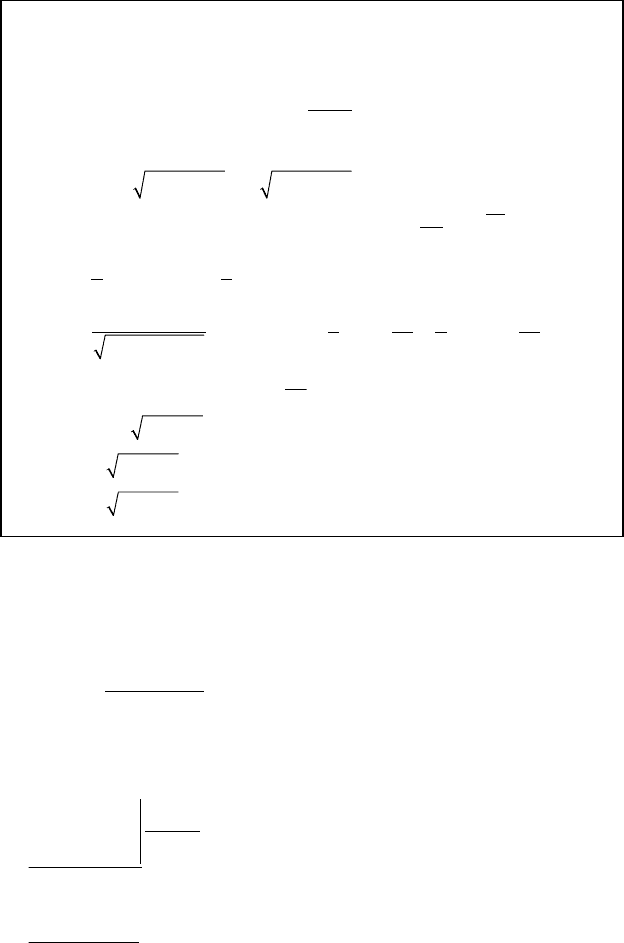
158
б) m = 2p, n = 2q ⇒ sin
2
x = (1 - cos2x)/2,
cos
2
x = (1 + cos2x)/2
3. ∫R(tgx)dx = ∫R*(t)dt,
если tgx = t, x = arctgt,
d
d
x
t
t
=
+1
2
.
16.3. интегрирование иррациональных функций
1.
Rx ax baxb xRtt
m
n
m
n
l
l
(, (),..., ())(),++=
∫∫
1
1
d*d
если ax + b = t
k
, k — общий знаменатель
m
n
j
j
,
jl= 1,,
x
a
tb
k
=-
1
(),
ddx
a
kt t
k
=
-
1
1
.
2.
Ax B
ax bx c
x
+
++
∫
2
d ,
замена
tx
bx
a
c
a
x
b
a
=++
′
=+
1
22
2
,
ax
2
+ bx + c = at
2
+ c -
b
a
2
4
.
3.
Rx axx(, ),
22
-
∫
d
замена х = asint,
Rx axx(, ,
22
+
∫
)d
замена x = atgt,
Rx xax(, ,
22
-
∫
)d
замена х = a/cost
Задачи к разд. 16.1
Вычислить интегралы:
1.
I
xx
x
x=
++
+
∫
32
2
5
3
d .
Решение: Под знаком интеграла — неправильная рациональная
дробь. Делим числитель на знаменатель для выделения целой час-
ти:
-
++
+
+
+
-
-+
+
-+
xx
xx
x
x
xx
x
x
32
3
2
2
2
5
3
3
1
35
3
32.
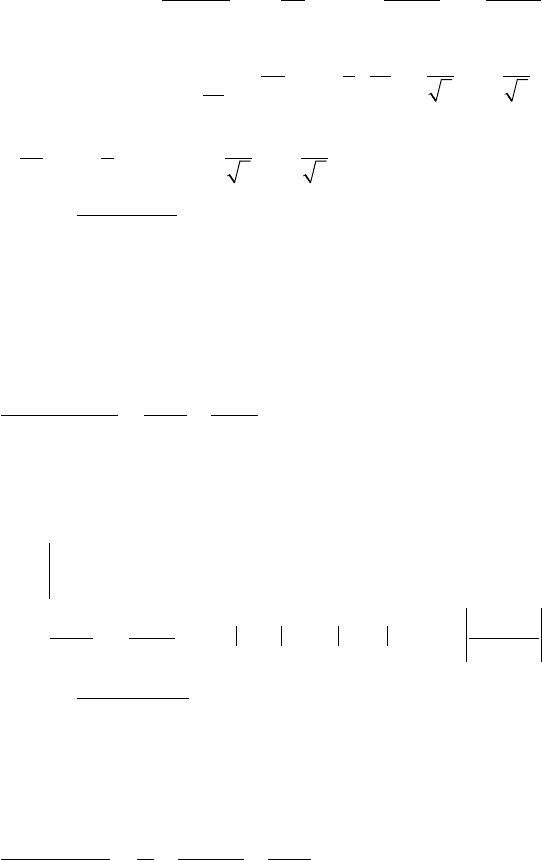
159
Тогда
Ixx
x
x
x
x
x
xx
x
x
x
xt
=+ +
-+
+
=+-
+
+
+
=
=
+=
∫∫ ∫∫
()
,
1
32
3
2
3
3
2
3
3
2
2
2
22
2
dd
dd
xxx txx
t
x
x
t
t
x
x
x
dd d
d
d
==
=+-+ =
=+-
∫
,
arctg
2
2
3
2
2
1
33
2
3
2
2
22
3
2
33
2
ln()arctg.x
x
c++ +
2.
I
xx
xx
=
-+
∫
d
2
32
.
Решение: Под знаком интеграла — правильная рациональная
дробь, причем знаменатель раскладывается на простые множители:
xx
xx
xx xx
2
12
2
320
12
32 12
-+=
==
⇒-+= --
,
,
()().
Тогда раскладываем дробь на сумму простейших дробей:
x
xx
A
x
B
x()()
.
--
=
-
+
-12 12
Неизвестные коэффициенты A и B находим, приводя дроби
справа к общему знаменателю и приравнивая числители справа и
слева. Получим тождество, справедливое при любых x:
A(x - 2) + B(x - 1) = x,
x
x
A
B
A
B
=
=
-=
=
⇒
=-
=
1
2
1
2
1
2
,
,
имеем
I
x
x
x
x
xxc
x
x
c=
-
-
+
-
=- -+ -+=
-
-
+
∫∫
dd
1
2
2
12 2
2
1
2
ln ln ln
()
.
3.
I
xx
xxx
x=
-+
-+
∫
233
2
2
32
d .
Решение: Знаменатель x
3
- 2x
2
+ x = x(x - 1)
2
имеет простой
корень x = 0 и корень x = 1 кратности 2, поэтому разложение на
простейшие дроби данной правильной рациональной дроби имеет
вид
233
11
1
2
22
xx
xx
A
x
B
x
C
x
-+
-
=+
-
+
-
⇒
() ()
A(x - 1)
2
+ Bx + Cx(x -
- 1) = 2x
2
- 3x + 3 ⇒ x
2
(A + C) + x(-2A + B - C) - A =
= 2x
2
- 3x + 3.
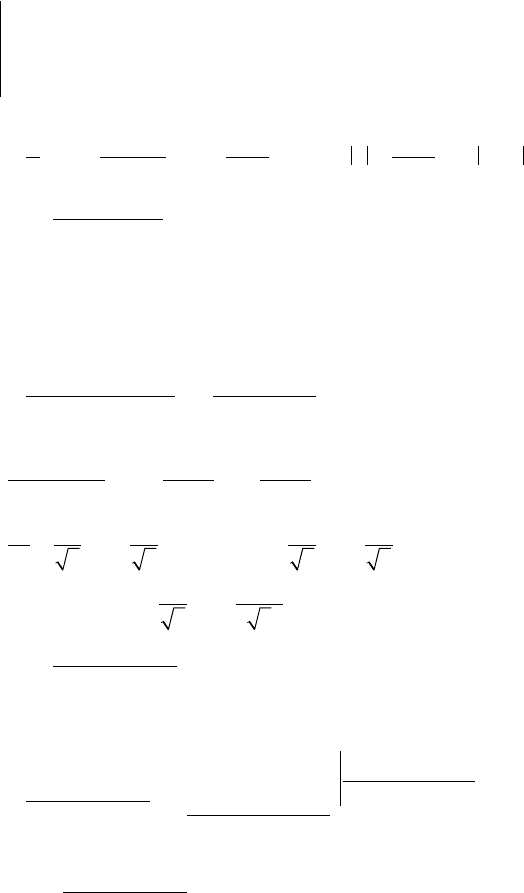
160
Приравниваем коэффициенты при одинаковых степенях x:
x
x
x
AC
ABC
A
C
BC
A
C
2
0
2
23
3
32
63
3
1
+=
-+-=-
=
⇒
+=
-+ -=-
=
⇒
=-,
,
,,
,B
A
+=
=
⇒13
3
⇒ A = 3, B = 2, C = -1 ⇒
I
x
x
x
x
x
xx
x
xc=+
-
+
-
-
=-
-
--+
∫∫ ∫
32
1
1
1
3
2
1
1
2
ddd
()
ln ln .
4.
I
xx
xx
=
-
++
∫
()
.
23
410
2
d
Решение: Дискриминант квадратного уравнения x
2
+ 4x + 10 =
= 0: ∆ = 16 - 40 < 0, поэтому знаменатель не имеет действитель-
ных корней. Под знаком интеграла — простейшая дробь третьего
типа:
I
xx
xx
xx
x
xt
xt
xt
=
-
+++
=
-
++
=
+=
=-
=
∫∫
()
()
()
()
,
,
23
446
23
26
2
2
22
dd
dd
=
=
--
+
=
+
-
+
=
+=
∫∫∫
223
6
2
6
7
6
6
2
222
2
() ,t
t
t
tt
t
t
t
tz
t
d
dd
dttz
z
z
t
t
t
c
x
=
=
=- =+-+=
=
∫
d
d7
66
6
7
66
2
arctgln( )arctg
ln(
22
410
7
6
2
6
++-
+
+x
x
c)arctg .
5.
I
xx
xx
=
+
++
∫
()
()()
.
3
2
3
11
d
Решение: Так как под знаком интеграла неправильная дробь, то
выделим целую часть:
I
xx
xx
x
xxx
xxx
xx
=
+
++
=
-
+
+++
+++
--+
∫
()
()()
3
2
3
32
32
2
3
11
3
1
1
1
2
d
=
=-
+-
++
∫∫
ddx
xx
xx
x
2
2
2
11()()
.
