Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Нуриева С.Н., Дегтярева О.М. Математика в примерах и задачах
Подождите немного. Документ загружается.

181
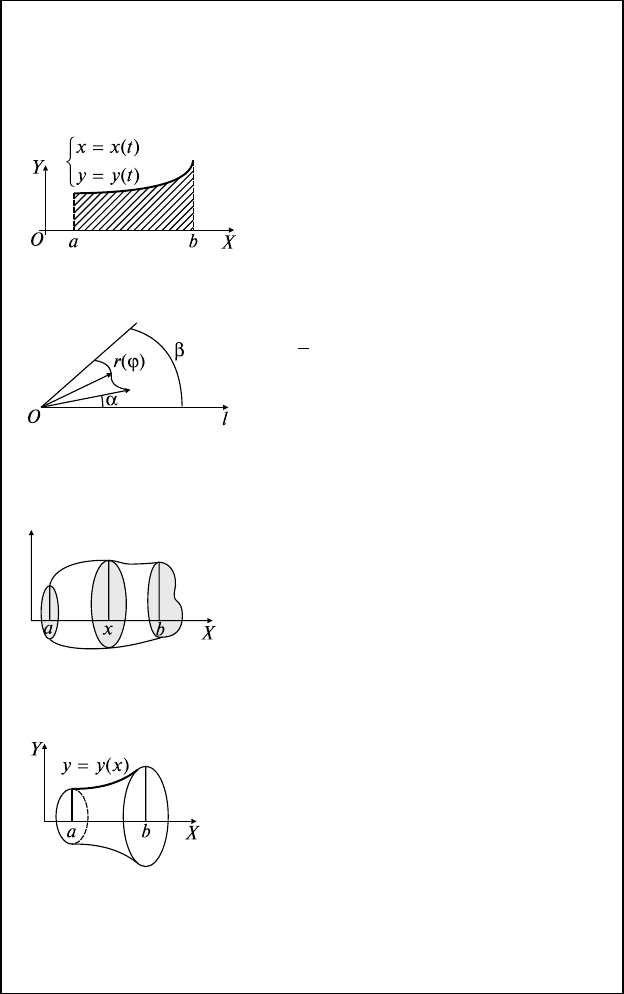
2. Площадь криволинейной трапеции при параметрическом зада-
нии кривой
∂
== ==
==<=
D
xxtyyt xaxb
xaxbab y
:
(),(), () ,()
,(),
αβ
0
Sytx t
Dt
=
′
∫
() d
α
β
3. Площадь криволинейного сектора в полярных координатах
∂D: r = r(ϕ), α ≤ ϕ ≤ β
Sr
D
=
∫
1
2
2
[( )]ϕϕ
α
β
d
18.2. Вычисление объемов тел
1. Объем тела Ω по известным площадям поперечных сечений
Известны площади сечений S(x) тела Ω плоскостями ⊥ OX,
axbV Sx x
D
a
b
≤≤⇒=
∫
()d
2. Объем тела вращения
Криволинейная трапеция D, ∂D: y = y(x), x = a, x = b (a < b),
y = 0, вращается вокруг оси ОХ ⇒ S(x) = π[y(x)]
2
,
Vyxx
x
a
b
=
∫
π [()]
2
d
Криволинейная трапеция D,
∂D: x = x(y), y = c, y = d (c < d), x = 0, вращается вокруг
оси ОY ⇒
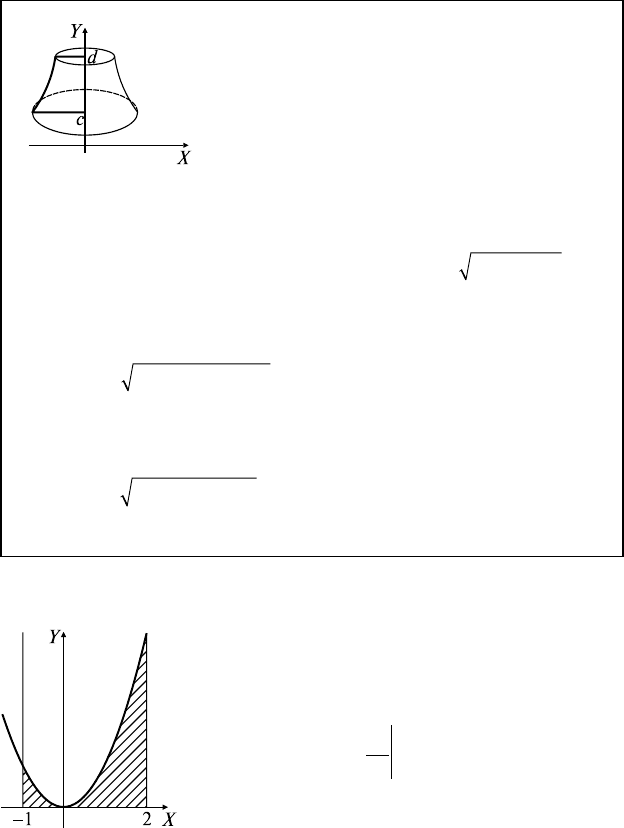
182
Sy xy Vxyy
y
c
d
() [()] ,[()]==
∫
ππ
22
d
18.3. Вычисление длины дуги кривой L
1. Длина дуги в прямоугольной системе координат
L: y = y(x), x ∈ [a, b], y′(x) ∈ C
[a,b]
⇒
lyxx
a
b
=+
′
∫
1
2
(()) d
2. Длина дуги при параметрическом задании L
L: x = x(t), y = y(t), t ∈ [α, β], x′(t), y′(t) ∈ C
[α,β]
⇒
⇒=
′
+
′
∫
lxtytt(()) (())
22
d
α
β
3. Длина дуги в полярных координатах
L: r = r(ϕ), ϕ ∈ [α, β], r′(ϕ) ∈ C
[α, β]
⇒
⇒
lr r=+
′
∫
22
() (())ϕϕϕ
α
β
d
Задачи к разд. 18.1
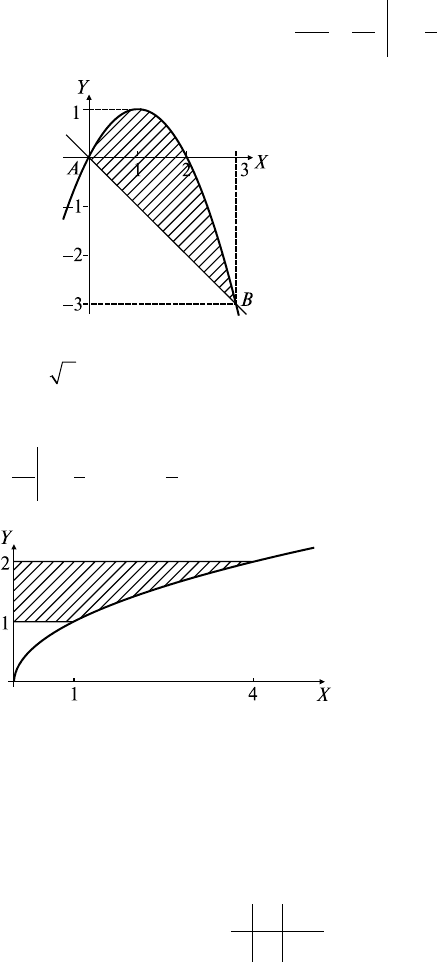
Задача 1. ∂D: y = x
2
, x = -1, x = 2, y = 0. Найти S
D
.
Решение: Граница области D (∂D) образо-
вана параболой y = x
2
, прямыми x = -1,
x = 2 и осью OX (рис. 18.1). Это криволиней-
ная трапеция, поэтому
Sxx
x
D
===
-
-
∫
2
1
2
3
1
2
3
3d .
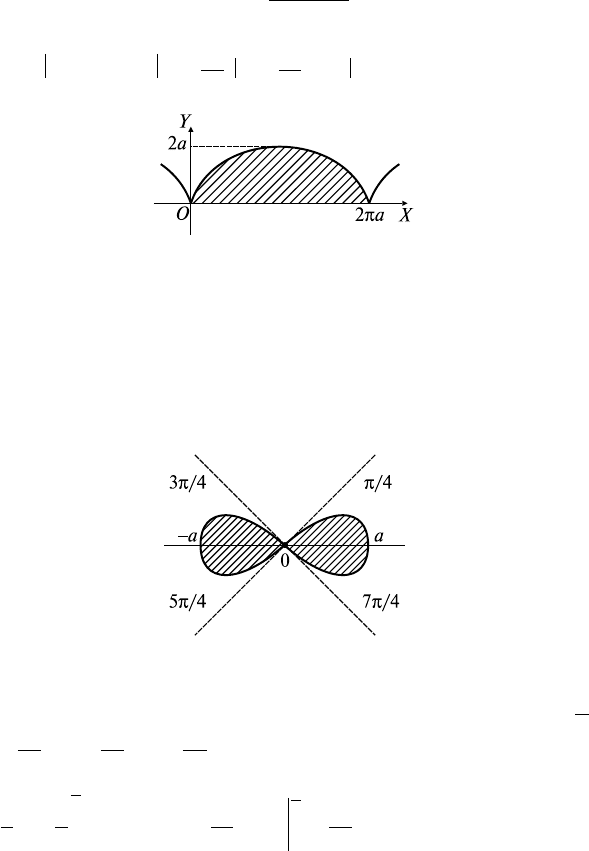
Задача 2. ∂D: y = -x, y = 2x - x
2
. Найти
S
D
.
Решение: Находим точки пересечения параболы y = 2x - x
2
и
прямой y = -x:
2x - x
2
= -x ⇒ x
2
- 3x = 0 ⇒ x
1
= 0, x
2
= 3 ⇒ A(0, 0),
B(3, -3).
Рис. 18.1
183
Строим область D (рис. 18.2) и вычисляем площадь:
Sxxxxxxx
xx
D
=--- =- =-
=
∫∫
[( )( )] () .23
3
23
9
2
2
0
3
2
0
3
23
0
3
dd
Рис. 18.2
Задача 3. ∂D: y =
x,
y = 1, y = 2, x = 0. Найти S
D
.
Решение: Имеем криволинейную трапецию, прилежащую к
оси OY (рис. 18.3):
Syy
y
D
===-=
∫
2
1
2
3
1
2
3
1
3
81
7
3
d ().
Рис. 18.3
Задача 4. ∂D: y = a(1 - cost), x = a(t - sint), y = 0,
0 ≤ x ≤ 2πa. Найти S
D
.
Решение: Область D ограничена первой аркой циклоиды и осью
OX (рис. 18.4). Это криволинейная трапеция при параметрическом
задании кривой:
Syx
ya txat t
xa tt
xa
t
D
a
==
=- =-
=-
∫
d
dd
0
2
1
1
02
0
π
π
(cos ), (sin ),
(cos ),
22π
=
184
=- =-+=
=-
∫∫
∫
atta ttt
ata
22
0
2
22
0
2
2
0
2
2
112
2
(cos )(coscos )
co
dd
d
ππ
π
ss
cos
sins
tt a
t
t
at at
a
t
a
dd
0
2
2
0
2
2
0
2
2
0
2
2
0
2
2
12
2
2
24
ππ
ππ
π
∫∫
+
+
=
=- ++
iin .23
0
2
2
ta
π
π=
Рис. 18.4
Задача 5. ∂D: (x
2
+ y
2
) = a
2
(x
2
- y
2
). Найти S
D
.
Решение: Кривая с данным уравнением называется лемнискатой
Бернулли. Для ее построения и вычисления ограниченной ею пло-
щади удобно перейти к полярной системе координат:
x = rcosϕ, y = rsinϕ ⇒ r
4
= a
2
r
2
(cos
2
ϕ - sin
2
ϕ) ⇒
⇒ r
2
= a
2
cos
2
ϕ.
Рис. 18.5
Для построения кривой (рис. 18.5) находим: r
max
= a при
cos2ϕ = 1, т.е. ϕ
0
= 0, ϕ
1
= π; r
min
= 0 при cos2ϕ = 0, т.е.
ϕ
π
0
4
= ,
ϕ
π
1
3
4
= ,
ϕ
π
2
5
4
= ,
ϕ
π
3
7
4
= .
Вычислим четвертую часть площади:
1
4
1
2
2
4
2
4
2
0
4
2
0
4
2
2
Sa
aa
Sa===⇒=
∫
cossin .ϕϕ ϕ
π
π
d
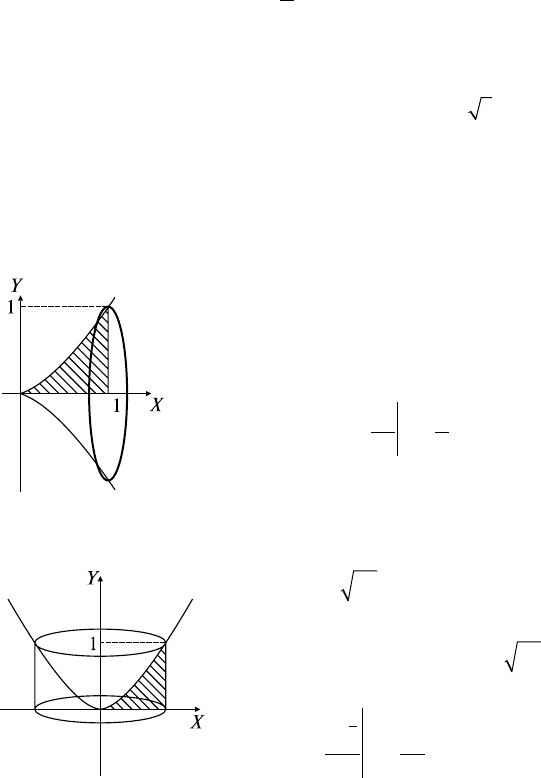
185
Задачи для самостоятельного решения
Найти площади S
D
областей со следующими границами:
1) ∂D: y = x
2
+ 1, x = 3, x = 0, y = 0;
2) ∂D: y = x
2
, y = 2x + 3; 3) ∂D: y = 3 - 2x - x
2
, y = 0;
4) ∂D: y = x
2
+ 4x, y = x + 4; 5) ∂D: y = 4 - x
2
, y = x
2
- 2x;
6) ∂D: xy = 1, x = 2, y = x; 7) ∂D: y
2
= 2x + 4, x = 0;
8) ∂D: y
2
= -x + 1,
y
x
2
4
1=- + ;
9) ∂D: y
2
= 2x + 1, x - y - 1 = 0;
10) ∂D: x = 3cost, y = 2sint; 11) ∂D: x = acos
3
t, y = asin
3
t;
12) ∂D: r = a(1 + cosϕ); 13) ∂D: r = 4sin
2
ϕ;
14) ∂D: x
2
+ y
2
= 1, x
2
+ y
2
= 4, y = x, y = x
3
(y > 0);
15) ∂D: x
2
+ y
2
- 2x = 0, y = x (y > 0).
Задачи к разд. 18.2
Задача 1. ∂D: y
2
= x
3
, x = 1, y = 0. Найти: а) V
x
; б) V
y
(объемы
тел, полученных при вращении D вокруг OX и OY соответ-
ственно).
Решение: а) при вращении области D вокруг
оси OX получаем тело, изображенное на
рис. 18.6, объем которого вычисляется по фор-
муле
Vxx
x
x
===
∫
ππ
π
3
0
1
4
0
1
44
d ;
б) объем тела вращения вокруг оси OY
(рис. 18.7) находится как разность объемов
V
y
1
цилиндра и
V
y
2
тела, образованного вращением
криволинейной трапеции с границей
∂D*:
xy=
2
3
,
y = 1, x = 0.
Тогда
VVVyyy
y
yyy
=-=- =
=- =
∫∫
12
0
1
2
3
2
0
1
7
3
0
1
3
7
4
7
ππ
ππ
π
dd()
.
Рис. 18.6
Рис. 18.7

186
Задача 2. ∂D: y = e
x
, x = 0, y = 0 (x < 0). Найти V
x
.
Решение: Имеем бесконечное тело вращения (рис. 18.8). Ис-
пользуя определение несобственного интеграла 1-го рода и фор-
мулу ОК, разд. 18.2, находим
Vx
x
xx
===-=
-∞
-∞
-∞
∫
π
ππ π
ed eee
2
0
2
0
0
22 2
().
Рис. 18.8
Задачи для самостоятельного решения
16) ∂D: y = x
3
, y = 0, x = 2. Найти: а) V
x
; б) V
y
.
17) ∂D: y = 2x - x
2
, y = 0. Найти V
x
.
18) ∂D: x
2
- y
2
= 4, y = ±2. Найти V
y
.
19) ∂D: y = 1 - x
2
, x + y = 1. Найти V
y
.
20) ∂D: x = acos
3
t, y = asin
3
t. Найти V
y
.
Задачи к разд. 18.3
Задача 1. Дана дуга AB:
yx=
3
;
A(0, 0), B(4, 8). Найти длину l
дуги AB.
Решение: Дуга задана в прямоугольной системе координат. Ее
длина
lxxxxxx=+
′
=+
=+
∫∫
11
3
2
1
9
4
3
2
2
0
4
1
2
2
0
4
0
4
ddd
∫∫
=
=
+
⋅= -
21
9
4
3
4
9
8
27
10 1
3
2
0
4
3
x
().
187
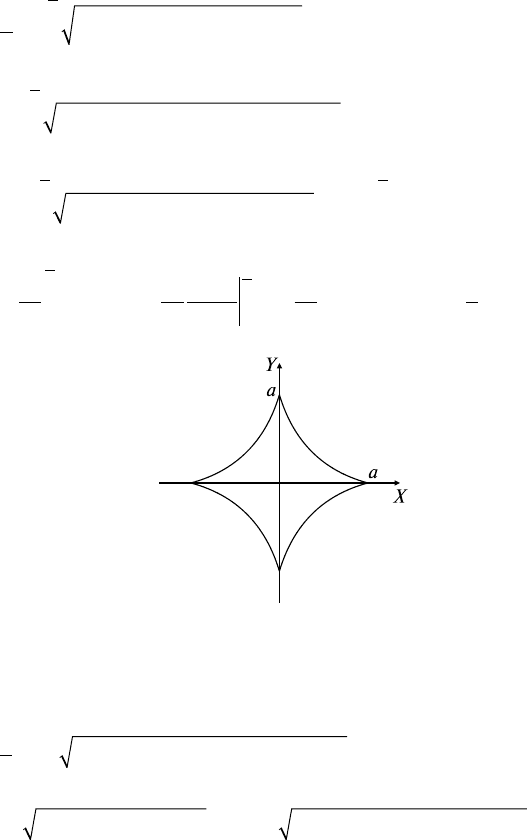
Задача 2. L: x = acos
3
t, y = asin
3
t. Найти l.
Решение: Находим длину четвертой части астроиды (рис. 18.9),
заданной параметрически:
1
4
33
3
2
3
2
0
2
22
latatt
att
=
′
(
)
+
′
(
)
=
=⋅+
∫
(cos )(sin)
(cos sin) (sin
d
π
222
0
2
22 22
0
2
33
ttt
attttt at
⋅=
=⋅⋅+ =
∫
∫
cos)
cossin (cos sin) sin
d
d
π
π
⋅⋅ =
==-=--
∫
∫
cos
sin
cos
(cos cos)
tt
a
tt
at a
d
d
0
2
0
2
0
2
3
2
2
3
2
2
2
3
4
0
π
π
π
π ==⇒=
3
2
6al a.
Рис. 18.9
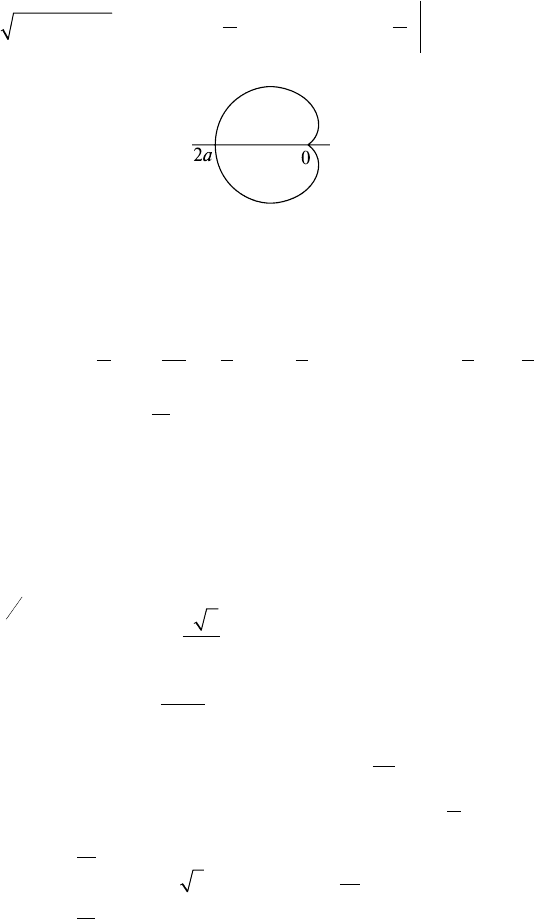
Задача 3. L: r = a(1 - cosϕ). Найти l.
Решение: Находим длину половины кардиоиды (рис. 18.10), за-
данной в полярных координатах:
1
2
11
1
22
0
22
0
la a
a
=- +-
′
=
-+ =
∫
∫
(( cos))((cos ))
(cos )sin
ϕϕϕ
ϕϕϕ
π
π
d
d
aa 12
22
0
-++=
∫
coscos sinϕϕϕϕ
π
d
188
aaaala21 2
2
22
2
48
00
0
(cos )sin cos.-= =⋅-
=⇒=
∫∫
ϕϕ
ϕ
ϕ
ϕ
ππ
π
dd
Рис. 18.10
Задачи для самостоятельного решения
Найти длины дуг следующих кривых:
21) L:
y
x
=
2
2π
π
lnsin,
1
2
3
2
≤≤x ;
22) L:
xy y=-
1
4
1
2
2
ln ,
1 ≤ y ≤ 2; 23)
x
t
t=-
3
3
,
y = t
2
+ 2, 0 ≤ t ≤ 3; 24) L: x =
= a(t - sint), y = a(1 - cost), 0 ≤ t ≤ 2π; 25) L: r = aϕ,
0 ≤ ϕ ≤ 2π.
варианты контрольной работы
Вариант № 1
1.
cos.
3
0
4
xxd
π
∫
Ответ:
52
2
.
2.
xx
x
ed
-
∫
0
1
.
Ответ:
e
e
- 2
.
3. ∂D: y = x
2
, y = 8 - x
2
. S
D
= ? Ответ:
64
3
.
4. ∂D: xy = 1, x = 2, x = 3, y = 0. V
x
= ? Ответ:
π
6
.
5. L:
x
t
y
t
t
=
=
≤≤
2
3
2
6
05
,
,
.
l = ? Ответ:
19
6
.
189
Вариант № 2
1.
sincos .
3
0
2
2
xxx
π
∫
⋅ d
Ответ:
2
15
.
2.
xxx
e
ln .d
1
∫
Ответ:
e
2
4
1
4
+ .
3. ∂D: y = -x
2
+ 4, y = 0. S
D
= ? Ответ:
10
2
3
.
4. ∂D: y = x, y = 2x, y = 1. V
y
= ?. Ответ:
π
4
.
5. L:
xt
yt
t
=
=
≤≤
1
3
1
2
03
3
2
,
,
.
l = ? Ответ:
7
3
.
Вариант № 3
1.
xxx
0
3
∫
arctg.d
Ответ:
2
3
3
2
π- .
2.
sincos .
2
0
2
xxx
π
∫
⋅ d
Ответ:
π
8
.
3. ∂D: y = e
x
, y = e
2x
, x = 1. S
D
= ? Ответ:
1
2
1
2
().e -
4. ∂D: x = -y
2
+ 1, x = 0. V
y
= ? Ответ:
406
15
π.
5. L:
xt
yt
t
=
=
≤≤
2
3
2
3
01
,
,
.
l = ? Ответ:
2
3
22 1().-
дополнительные задания к вариантам контрольной работы
1. Как вычисляется S
D
?
∂=
=
=<
==
D
yr
yr rr
1
21 2
(),
()(()()),
,.
ϕ
ϕϕ ϕ
ϕαϕβ
2. Как вычисляется V
x
?
∂=
=
=<<
==<
D
yfx
yfxfxfx
xaxbab
1
212
0
(),
()(()()),
,().

190
расчетное задание
Задание 1. Вычислить определенный интеграл:
а)
xxcx
mn
l
a
b
(( ))-+
∫
1
2
2
d
;
N m n l a b c
1 2 1 -1 0 1 4
2 4 2 -7 0 1 1
3 4 2 -7
2
2 -1
4 4 1 -7 0 1 2
5 2 2 -5 1 3 3
6 2 2 -5 2
2
2
-2
7 2 1 1 0 1 1
8 2 2 -5 0 2 4
9 0 2 -3 2
2
3
-3
10 2 1 -5 0 1 4
11 2 2 -7 0
6
6
2
12 0 2 -3 2
6
-3
13 0 1 3 0
3
3
14 0 2 -5 0
2
2
15 -2 2 -3 2
2
3
-3
16 0 1 -3 1
3
4
17 -2 2 -3 1
3
3
18 -4 2 1 1 2 -1
19 -2 1 -3 1
2
4
20 -2 2 -1
2
6
2
21 -6 2 3
2
2 -2
22 -2 1 1
3
3 12
23 -4 1 1 1 2 4
24 -4 2 1
2
6
6
25 -8 2 5 2 4 -4
26 -4 1 -1
2
2 8
27 -6 2 3
3
3 3
28 -8 2 3 1
2
-1
