Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Нуриева С.Н., Дегтярева О.М. Математика в примерах и задачах
Подождите немного. Документ загружается.


191
N m n l a b c
29 -4 2 -1 1
3
3
30 -6 2 1
3
2 -3
б)
()() .Cx Cx Cfxx
a
b
1
2
23
++
∫
d
N a b C
1
C
2
C
3
f(x)
1 3 4 0 2 -4 ln(x - 2)
2 0
3
3 6 0
arctg
x
3
3 0
π
4
0 2 -1 sin4x
4 0
π
0 2 3 cos3x
5 0 1 0 2 5 e
2x
6 4 5 3 2 0 ln(x - 3)
7 0 2 3 4 0
arctg
x
2
8 0
π
0 3 1 sinx
9 0
π
2
0 1 -3 cos2x
10 0 1 0 2 3 e
3x
11 5 6 3 1 0 ln(x - 4)
12 0 1 3 2 0 arctgx
13 0
π
2
0 -3 1
sin
x
2
14 0
π
0 2 5
cos
x
3
15 0 1 0 3 -4
e
x
4
16 2 3 -3 4 0 ln(x - 1)
17 0
2
3 6 0
arctg
x
2
18 0
π
6
3 -2 0 sinx
19 0
π
4
1 0 0 cos4x
20 0 1 0 3 -1 e
-x
21 3 4 1 0 -2 ln(x - 2)
22 0
3
3 4 0
arctg
x
3

192
N a b C
1
C
2
C
3
f(x)
23 0 1 1 -2 0
e
x
2
24 4 5 1 0 0 ln(x - 3)
25 0 2 1 0 0
arctg
x
2
26 0
π
3 4 0 sinx
27 0
π
2
3 6 0 cosx
28 0 1 3 2 0 e
-x
29 0
π
0 2 -3
sin
x
4
30 -1 0 0 2 1 ln(x + 2)
Задание 2.
Вычислить площадь фигуры, ограниченной линиями:
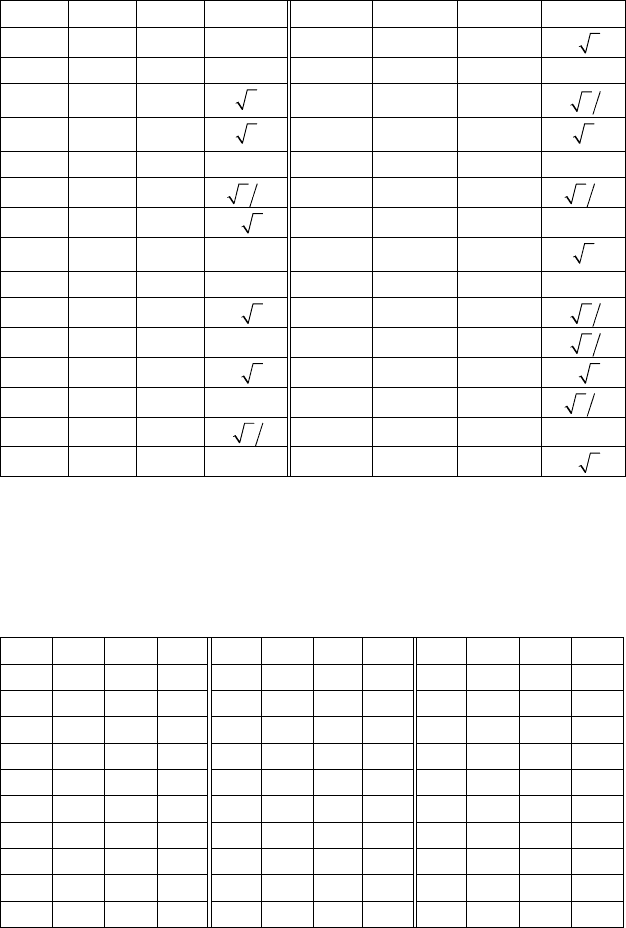
а) y = ax
2
+ bx + c, bx - 2y + 2c = 0;
N a b c N a b c
1 2 7 -4 16 4 -11 -3
2 3 8 -3 17 3 8 -4
3 2 9 4 18 -5 9 2
4 3 14 -5 19 -2 3 9
5 1 -1 6 20 -5 -8 4
6 1 -3 -10 21 -2 3 9
7 3 -7 -6 22 -4 -11 3
8 -2 9 -4 23 6 5 -1
9 -3 14 15 24 4 -3 -1
10 -1 -3 10 25 2 9 10
11 5 9 -2 26 2 5 3
12 2 3 -9 27 -2 7 -6
13 5 -8 -4 28 3 -10 3
14 3 4 -4 29 4 -13 3
15 2 3 -9 30 2 7 6
193
б) x
2
+ y
2
+ ax + by = 0, y = cx,
y + x + (-1)
n
y + (-1)
n+1
x = 0.
N a b c N a b c
1 1 2 1 16 5 -1
- 3
2 -2 1 -1 17 -1 5 -1
3 3 4
3
18 -4 3
- 33
4 -4 -3
3
19 1 3
3
5 1 -2 -1 20 -1 3 -1
6 3 2
33
21 3 1
33
7 2 -3
- 3
22 4 1 1
8 4 -1 -1 23 3 4
3
9 2 5 1 24 3 -5 -1
10 -5 2
- 3
25 5 -2
- 33
11 3 -2 -1 26 1 -3
- 33
12 2 -1
- 3
27 -1 4
- 3
13 4 -3 -1 28 -2 -1
33
14 -3 2
- 33
29 -3 1 -1
15 -4 -1 1 30 -2 3
- 3
Задание 3.
Определить объем тела, образуемого вращением фигуры D с
границей:
а) y = 0, x = b, x = c, y = (-1)
N
(Ae
ax
+ B); вокруг оси OX;
A, B — две цифры номера группы;
N a b c N a b c N a b c
1 -1 -1 1 11 4 2 3 21 -3 -5 0
2 -2 0 2 12 5 1 5 22 -4 -4 3
3 3 1 3 13 4 -4 0 23 -5 -3 5
4 -4 -2 1 14 -5 -3 1 24 3 -2 -1
5 5 -3 0 15 -1 3 5 25 4 -4 1
6 2 -4 -2 16 2 2 5 26 -5 0 5
7 -3 -1 2 17 -3 -3 3 27 4 -1 1
8 -4 0 4 18 -4 2 4 28 5 -4 4
9 -5 -1 3 19 5 -3 2 29 -1 -3 -2
10 3 -2 2 20 2 0 5 30 -2 -1 5

194
б)
xa t
yb tc
yb cy bc
t
=
=+
=+=+
≤≤
cos,
sin,
sin, sin,
;
βα
βα
вокруг оси OY.
N a b c
α β
N a b c
α β
1 1 2 -1 π/4 0 16 4 6 -4 -π/6 -π/2
2 2 3 1 π/3 0 17 5 6 2 π/3 π/6
3 3 4 2 π/2 π/6 18 3 2 -2 -π/6 -π/4
4 4 5 1 0 -π/3 19 4 3 1 π/2 π/3
5 1 3 -1 0 -π/4 20 5 4 1 -π/4 -π/2
6 2 4 -2 π/2 0 21 6 5 -1 -π/4 -π/3
7 3 5 2 -π/3 -π/2 22 4 2 1 π/4 0
8 1 4 3 0 -π/3 23 5 3 2 π/2 π/6
9 2 5 -3 π/3 π/4 24 5 2 -1 0 -π/2
10 3 4 1 π/6 0 25 6 4 3 -π/3 -π/2
11 1 5 1 π/2 π/4 26 6 3 1 π/2 -π/2
12 2 4 -1 -π/6 -π/3 27 6 2 -1 π/3 π/6
13 1 6 3 π/2 -π/2 28 4 4 3 -π/4 -π/2
14 2 6 3 π/4 π/6 29 2 4 2 π/3 0
15 3 6 4 0 -π/2 30 4 5 -2 0 -π/3
Задание 4.
Определить длину кривой
xat
ybtc
tm
=
=+
≤≤
3
2
0
5
3
,
,
,
где
m
b
a
= .
N a b c N a b c N a b c
1 4 2 1 11 -2 2 -3 21 19 1 4
2
19
1 -2 12 2 4 4 22 19 3 4
3 6 3 3 13 3 3 2 23 4 6 0
4
-
19
1 4 14 2 1 1 24 -4 4 6
5 2 2 5 15 -2 1 -1 25
2
19
4 -7
6 2 3 -1 16 -2 3 3 26 2 3 -8
7 1 3 3 17 4 6 -2 27 -2 3 0
8 1 6 -4 18 1 2 1 28
3
19
1 1
9 -1 3 -5 19 -4 6 3 29 3 1 2
10 -1 6 0 20 -1 2 -3 30 -3 6 -3
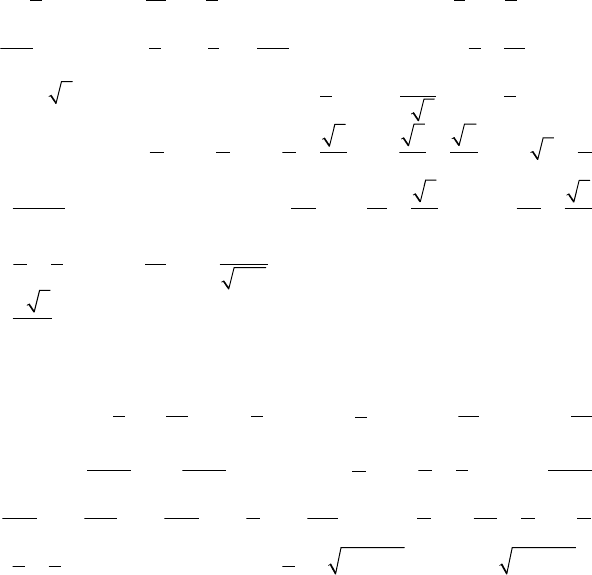
195
Теоретические вопросы
1. Дайте определение определенного интеграла.
2. Каковы свойства определенного интеграла?
3. Как связаны определенный и неопределенный интегралы?
4. Каковы методы интегрирования определенного интеграла?
5. Каковы приложения определенного интеграла?
ответы к разд. 17, 18
17. Определенный интеграл
1)
1
2
1
6
();e -
2)
π
12
;
3)
7
3
;
4) arctg3 - arctg2; 5)
33
1
3
;
6)
3
2
π;
7) 3π;
8)
248
9
;
9) 12; 10)
6
2
3
;
11)
3
8
2
2
π+
ln
;
12) 0,125 Дж; 13)
2
3
10
7
3ln +
ед.;
14)
ee- ;
15) π/6; 16) 2; 17)
2
7
;
18)
π
33
;
19)
3
2
41(ln);-
20) 7 + 2ln2; 21)
π
6
;
22)
π
6
;
23)
π
3
3
2
+ ;
24)
3
2
2
2
- ;
25)
3
3
-
π
;
26)
e
e
2
2
3
4
-
;
27) 3(ln12 - 1); 28)
-
2
3
π
;
29)
π
12
3
2
1+-;
30)
2
3
3
2
π
- ;
31)
π
4
1
2
- ;
32)
1
3
2
-
e
;
33)
2
2ln
;
34) Расходится; 35) Расходится;
36)
π 5
5
;
37) Расходится; 38) Расходится; 39) 6; 40) Расходится.
18. Геометрические приложения определенного интеграла
1) 12; 2)
10
2
3
;
3)
32
3
;
4)
20
5
6
;
5) 9; 6)
3
2
2- ln ;
7)
16
3
;
8) 4; 9)
16
3
;
10) 6π; 11)
3
8
2
πa
;
12)
3
2
2
πa
;
13) 6π; 14)
π
8
;
15)
π
4
1
2
- ;
16) а)
128
7
π
;
б)
64
5
π
;
17)
16
15
π
;
18)
64
3
π
;
19)
π
6
;
20)
32
105
3
πa ;
21)
43
8
4
8π
π
π
π
ln tg ln tg ;-
22)
3
4
1
2
2+ ln ;
23) 12; 24) 8a; 25)
a
2
214214
22
(ln( )).ππ ππ++ ++

196
19. Элементы теории Функций
и ФункциональноГо анализа
опорный конспект № 19
19.1. Мера Лебега. измеримые множества
R = (-∞, +∞), А ∈ R
О: M(m) — верхняя (нижняя) грань ⇔ a ≤ M (a ≥ m) ∀a ∈ A
M* = supA (m* = infA) — точная верхняя (нижняя) грань А
ℑ = [a, b] ∨ (a, b) ∨ [a, b) ∨ (a, b]
О: {ℑ} ⊂ R — покрытие А ⇔ ∀с ∈ A ∃ ℑ: c ∈ ℑ
О: Мера ℑ ⇔ µ(ℑ) = b - a
О: Внешняя мера А, А ⊂ [a, b] ⇔ µ*(A) =
inf().
∪ℑ ⊃
ℑ
∑
k
A
k
k
µ
Внутренняя мера А ⇔ µ*(A) = (b - a) - µ*(
A
),
A
= [a, b]\A
О: Ограниченное множество А измеримо с мерой µ(A) ⇔ µ*(A) =
= µ*(A) = µ(A)
19.2. измеримые функции. интеграл Лебега
О: f(x), x ∈ A, — измерима ⇔ А измеримо ∧ ∀ конечного с ∈ R
измеримо А( f(x) > c)
Т. (Лузина): f (x) — измерима и почти всюду конечна на
[a, b] ⇒ ∀δ > 0 ∃ϕ(x) ∈ C
[a,b]
: µA ( f(x) ≠ ϕ(x)) < δ
О:
fx E
E
y
ii
i
n
i
() lim()
max
dµηµ
∫
∑
=
→
=
∆ 0
1
— интеграл Лебега, где f(x) изме-
рима на измеримом Е,
m =
∈
inf(),
xE
fx
M =
∈
sup(),
xE
fx
[m, M] раз-
бивают на [y
i-1
, y
i
),
in= 1,,
∆y
i
= y
i
- y
i-1
, η
i
∈ [y
i
- y
i-1
),
E
i
= E (y
i-1
≤ f(x) < y
i
)
Т:
∃=
∫
fx xJ
a
b
()d
(Римана) ⇒
fx J
a
b
() .dµ
∫
=
19.3. Функции с ограниченным изменением (ФОи).
интеграл Стилтьеса
О: f(x), x ∈ [a, b], ФОИ ⇔ ∃с > 0: ∀ℑ
n
(a = x
0
< x
1
< ... < x
n
=
= b) ⇒
fx fx c
kk
k
n
() ();-≤
-
=
∑
1
1
Vf fx fx
a
b
kk
k
n
n
[] sup()().=-
ℑ
-
=
∑
1
1
О:
fx gx fgxgx
a
b
x
i
i
n
ii
i
() () lim()[ () ()]
max
d
∫
∑
=-
→
=
-
∆ 0
1
1
ξ
— интеграл Рима-
на—Стилтьеса, где f(x) ∈ C
[a,b]
, g(x) — ФОИ на [a, b], [a, b]
разбивается на [x
i-1
, x
i
],
in= 1,,
∆x
i
= x
i
- x
i-1
, ξ
i
∈ [x
i
- x
i-1
]
Задачи для самостоятельного решения к разд. 19.3
Показать, что для интеграла Стилтьеса выполняются свой-
ства:
1)
(()()) () () () () ();fx fx gx fx gx fxgx
a
b
a
b
a
b
12 12
+=+
∫∫∫
ddd
2)
fx gx gx fx gx fx gx
a
b
a
b
a
b
()(()()) () () () ();ddd
12 12
+= +
∫∫∫
3)
kf xkgx kk fx gx
a
b
a
b
12 12
()(()) () ().dd
∫∫
=

198
Глава 7
обыкновенные
диФФеренциальные уравнениЯ
20. обыкновенные диФФеренциальные уравнениЯ
I ПорЯдка
опорный конспект № 20
20.1. Основные понятия
F(x, y, y′, ..., y
(n)
) = 0 — ОДУ n-го порядка
y = ϕ(x) — решение ОДУ ⇔ F(x, ϕ(x), ϕ′(x), ..., ϕ
(n)
(x)) ≡ 0
20.2. ОДУ I порядка
F(x, y, y′) = 0 — ОДУ I порядка
y′ = f(x, y) — разрешенное относительно у′,
P(x, y)dx + Q(x, y)dy = 0 — другой вид
Задача Коши: y′ = f(x, y), y(x
0
) = y
0
Т: f(x, y), f ′
y
(x, y) — непрерывны в окрестности т. М
0
(x
0
, y
0
) ⇒
⇒ решение задачи Коши ∃! в окрестности т. х
0
Общее решение ОДУ при непрерывности f(x, y), f ′
y
(x, y) в D —
функция y = ϕ(x, c), c = const, если:
1) y = ϕ(x, c) — решение ОДУ ∀с;
2) ∀y(x
0
) = y
0
∃! c = c
0
: y = ϕ(x, c
0
) — решение задачи Коши,
(х
0
, у
0
) ∈ D
20.3. ОДУ с разделяющимися переменными
ОДУ, приводящиеся к виду f
2
(y)dy = f
1
(x)dx
а)
′
=⇔=y
fx
fx
y
x
fx
fy
1
2
1
2
()
()
()
()
d
d
(× f
2
(y)dx, интегрируем) ⇒
⇒
fyyfxx c
21
() () ;dd
∫∫
=+
б) P
1
(x)P
2
(y)dx + Q
1
(x)Q
2
(y)dy = 0
(:P
2
(y)Q
1
(x), интегрируем) ⇒
⇒
Px
Qx
x
Qy
Py
yc
1
1
2
2
()
()
()
()
dd
∫∫
=- +
20.4. Однородные ДУ I порядка
О: f(x, y) — однородная функция n-го измерения ⇔
⇔ f(λx, λy) = λ
n
f(x, y) для ∀λ
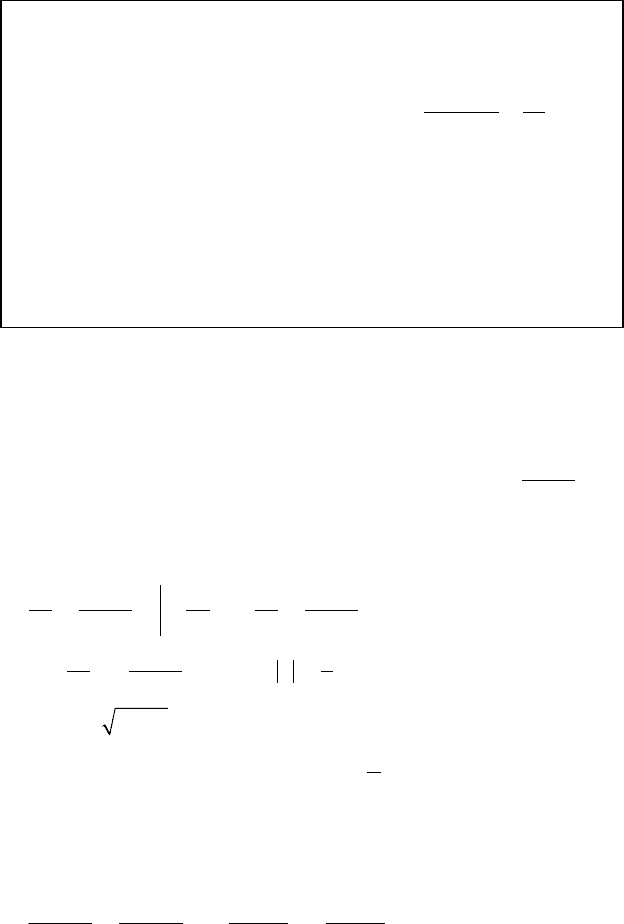
199
y′ = f(x, y) — однородное ДУ ⇔ f(λx, λy) = f(x, y) ⇔
⇔ f(x, y) = f *(y/x)
Замена y/x = u, y = xu ⇒ u + xu′ = f *(u)
ОДУ с разделяющимися переменными ⇔
d
*
du
fu u
x
x()
.
-
=
20.5. Линейные ДУ I порядка
y′ + p(x)y = q(x). Замена y = uv: y′ = u′v + uv′ ⇒
⇒ u′v + uv′ + p(x)uv = q(x) ⇔ u′v + u(v′ + p(x)v) = q(x)
1) v ′ + p(x)v = 0 — ОДУ с разделяющимися переменными,
ищем ∀ частное решение v = v(x)
2) u′v = q(x) — ОДУ с разделяющимися переменными, ищем
общее решение
Задачи к разд. 20.1–20.3
Решить следующие ОДУ I порядка:
1. y′(1 + x
2
) = xy.
Решение: Выразим из уравнения производную
′
=
+
y
xy
x1
2
.
Это
ОДУ с разделяющимися переменными (см. ОК, разд. 20.3а)). За-
меним производную отношением дифференциалов и затем разде-
лим переменные:
d
d
dddy
x
x
x
y
x
y
y
y
xx
x
=
+
⋅⋅
⇒=
+11
22
,
интегрируем ⇒
⇒=
+
+⇒ =++⇒
⇒= +
∫∫
dd
*
y
y
xx
x
cy xc
yc x
1
1
2
1
1
2
2
2
ln ln()ln
— решение данного ОДУ.
2. sinycosxdy = cosysinxdx;
y() .0
4
=
π
Решение: Это задача Коши для ОДУ с разделяющимися пере-
менными (см. ОК, разд. 20.2, 20.3 б)). Сначала найдем общее ре-
шение ДУ путем разделения переменных и последующего интег-
рирования:
sin
cos
sin
cos
cos
cos
cos
cos
yy
y
xx
x
y
y
x
x
c
dddd
*=⇒ =+⇒
∫∫
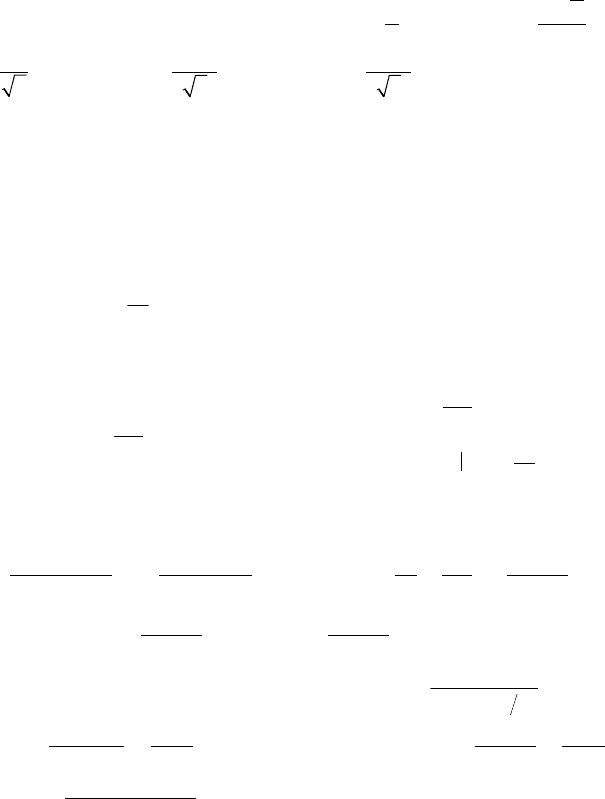
200
ln|cosy| = ln|cosx| + lnc ⇒ cosy = ccosx — общий интеграл.
Далее, используя начальное условие
y() ,0
4
=
π
находим
c
0
4
0
==
cos
cos
π
=
1
2
.
Тогда
cos
cos
y
x
=
2
или
y
x
= arccos
cos
2
— решение задачи
Коши, т.е. частное решение данного ОДУ, удовлетворяющее на-
чальному условию.
3. Торговыми учреждениями реализуется продукция B, о кото-
рой в момент времени t из числа потенциальных покупателей N
знает X покупателей. Скорость изменения числа знающих покупа-
телей пропорциональна как числу знающих, так и числу не зна-
ющих о продукции B покупателей. В начальный момент времени
о товаре знало
N
γ
человек. Найти X(t) (уравнение логистической
кривой).
Решение: Так как скорость изменения числа знающих поку-
пателей
V
X
t
=
d
d
,
то имеем задачу Коши:
d
d
X
t
kX NX
X
N
t
=-
=
=
(),
,
0
γ
где k > 0 — коэффициент пропорциональности. Получено ОДУ
1-го порядка с разделяющимися переменными. Умножаем его на
dd
d*
dd
*
t
kX NX
X
XN X
kt c
N
X
X
X
NX
kt c
X
() ()
ln
-
⇒
-
=+⇒+
-
=
=+⇒
∫∫ ∫∫
1
NNX
Nktc
X
NX
AAe
Nktc
-
=+⇒
-
==e ,.
Используя начальное условие, находим
N
NN
A
γγ()-
=⇒
⇒=
-
=
-
A
N
N()
,
γγ1
1
1
т.е. решение задачи Коши
X
NX
Nkt
-
=
-
e
γ 1
или
X
N
Nkt
=
+-
-
11()
.
γ e
4. Материальная точка массой m = 1 г движется прямолиней-
но под действием силы F, прямо пропорциональной времени t,
отсчитываемому от t = 0, и обратно пропорциональной скорости
движения v. Известно, что при t = 10 с скорость v = 0,5 м/с,
