Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Нуриева С.Н., Дегтярева О.М. Математика в примерах и задачах
Подождите немного. Документ загружается.


ние; 32)
xc c
kk
kk kk kk
rt rt
=++
++
12
24
13 24 15
12
ee ;
33)
x
V
t=
0
ω
ωsin,
ω
2
=
=
C
m
.
Указание: По закону Ньютона mx″ = -Cx, т.е. имеем задачу
Коши: x″ + ω
2
x = 0, x(0) = 0, x′(0) = v
0
.
22. ОДУ высших порядков и системы ДУ
1) y = c
1
cos3x + c
2
sin3x + c
3
; 2) x = c
1
e
-t
+ c
2
e
3t
, y =
= 2c
1
e
-t
- 2c
2
e
3t
; 3) x = e
t
(c
1
cos3t + c
2
sin3t), y = e
t
(-c
2
cos3t +
+ c
1
sin3t); 4) x = c
1
e
t
+ c
2
e
-t
+ tsht, y = c
1
e
t
- c
2
e
t
+ tcht + sht;
5)
xc c
t
tttt
=+++
-
-
12
33
14
16
eeee,
yc ct
tt tt
=-++ +
-
22
1
8
14
12
33
ee ee() ;
6)
k x
k
y
k
f(x
k
, y
k
)
0 -1 0,2000 5,000
1 -0,8 1,2000 0,6667
2 -0,6 1,33333 0,4500
3 -0,4 1,42333 0,2810
4 -0,2 1,47954 0,1352
5 0 1,50657 0,0000
6 0,2 1,50657 -0,1328
7 0,4 1,4800 -0,2703
8 0,6 1,42597 -0,4208
9 0,8 1,34182 -0,5962
10 1 1,22258 -0,81794
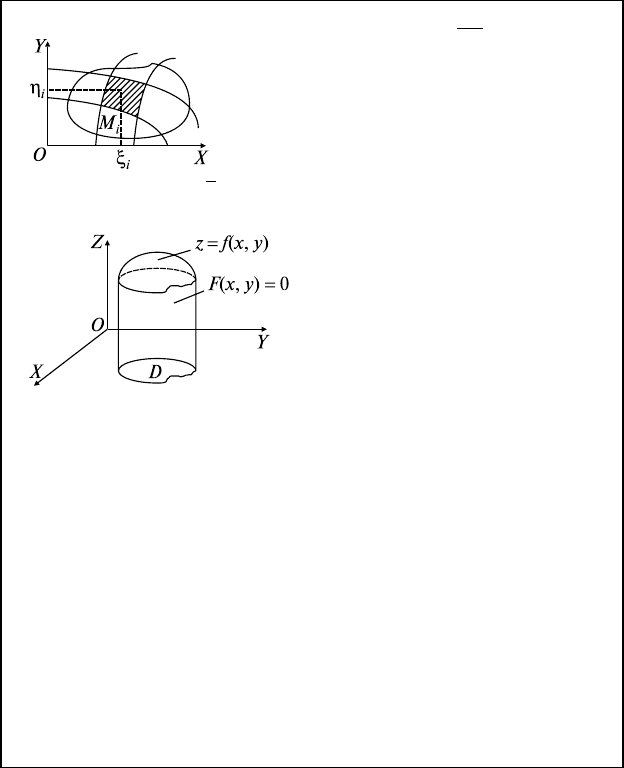
7)
x y x + h/2 k
1
y + k
1
/2 k
2
y + k
2
/2 k
3
y + k
3
k
4
0,00 1,00 0,100 0,200 1,100 0,260 1,130 0,153 1,153 0,311
0,20 1,223 0,300 0,325 1,385 0,397 1,421 0,262 1,4849 0,457
0,40 1,573 0,500 0,475 1,810 0,562 1,854 0,385 1,958 0,632
0,60 2,073 0,700 0,655 2,400 0,760 2,453 0,525 2,5982 0,840
0,80 2,750 0,900 0,870 3,185 0,997 3,249 0,685 3,4353 1,087
1 3,637
222
Глава 8
интеГрирование Функций
нескольких Переменных
23. двойной интеГрал
опорный конспект № 23
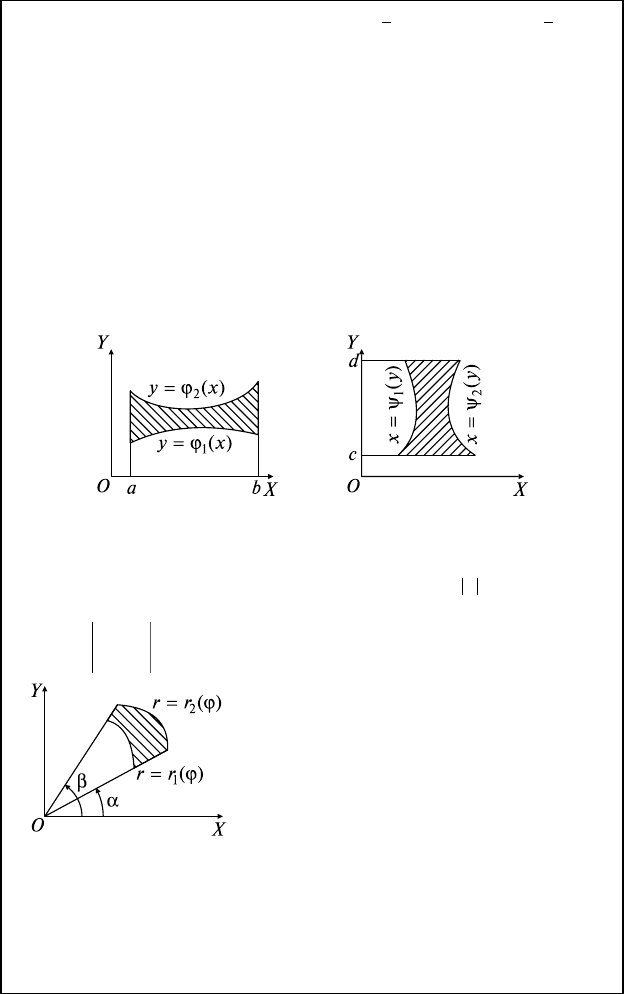
23.1. Определение Ди
D разбивается на ∆D
i
, i =
1,,n
с площадями ∆s
i
, ∆D
i
∩
∆D
j
= 0, i ≠ j,
M
i
(ξ
i
, η
i
) ∈ ∆D
i
⇒
⇒=
∫∫
∑
→
=
fxys fs
D
ii i
i
n
(, )lim (, )d
λ
ξη
0
1
∆
,
λ = maxdiam∆D
i
Т: f(x, y) непр. в
D
⇒ ДИ ∃
Цилиндрическое тело Ω ⇔ ∂Ω: z = f(x, y), z = 0, F(x, y) = 0 ⇒
⇒=
∫∫
Vfxy s
D
(, )d
23.2. Свойства Ди
1
0
.
[(,) (, )] (, )(,) .fxyxys fxys xy s
DDD
+= +
∫∫ ∫∫ ∫∫
ϕϕddd
2
0
.
cf xy scfxys
DD
(, )(,),dd
∫∫ ∫∫
=
c = const.
3
0
. D = D
1
+ D
2
⇒
fxys fxys fxys
DDD
(, )(,) (, ).ddd
∫∫ ∫∫ ∫∫
=+
12
4
0
.
dsS
D
∫∫
=
— площадь D.
5
0
. ϕ(x, y) ≤ ψ(x, y) в D ⇒
ϕψ(, )(,) .xy sxys
DD
dd
∫∫ ∫∫
≤
223
6
0
. Теорема о среднем: f(x, y) непр. в
D
⇒ ∃M(ξ, η) ∈
D
:
fxys fS
D
(, )(,).d
∫∫
=ξη
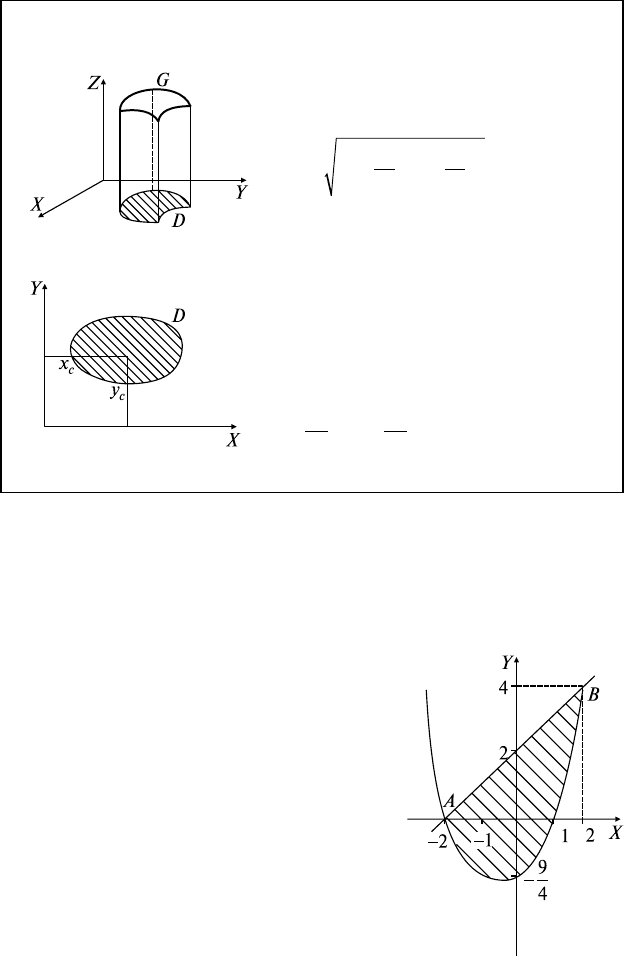
23.3. Вычисление Ди
∂D: y = ϕ
1
(x), y = ϕ
2
(x) (ϕ
1
(x) < ϕ
2
(x)), x = a, x = b (a < b) ⇒
⇒=
∫∫ ∫∫
fxys sfxy y
Da
b
x
x
(, )(,) ,
()
()
dd d
ϕ
ϕ
1
2
∂D: x = ψ
1
(y), x = ψ
2
(y) (ψ
1
(y) < ψ
2
(y)), y = c, y = d (c < d) ⇒
⇒=
∫∫ ∫∫
fxys yfxy x
Dc
d
x
x
(, )(,)
()
()
dd d
ψ
ψ
1
2
23.4. Ди в полярных координатах
xxuv
yyuv
DD fxys fuvJ uv
DD
=
=
↔⇒ =
∫∫ ∫∫
(, ),
(, ),
(, )(,)*d*dd
*
J
xx
yy
uv
uv
=
′′
′′
— якобиан
∂D: r = r
1
(ϕ),
r = r
2
(ϕ),
(r
1
(ϕ) < r
2
(ϕ))
ϕ = α, ϕ = β (α < β) ⇒
⇒= =
∫∫ ∫∫
fxys fr rrr
DD
(, )(cos,sin)dddϕϕ ϕ
=
∫∫
ddϕϕϕ
α
β
ϕ
ϕ
fr rrr
r
r
(cos ,sin )
()
()
1
2
224
23.5. Приложения Ди
1. Геометрические приложения
Вычисления площадей (см. разд. 23.2)
Вычисление объемов (см. разд. 23.1)
Вычисление площади поверхности G:
σ= +
∂
∂
+
∂
∂
∫∫
1
22
z
x
z
y
s
D
d .
2. Физические приложения
Статические моменты плоской пласти-
ны D:
µr µr
x
D
y
D
yxys xxys==
∫∫ ∫∫
(, ), (, ),dd
r — поверхностная плотность
Координаты центра масс D:
x
m
c
y
=
µ
,
y
m
c
x
=
µ
,
mxys
D
=
∫∫
r(, )d
—
масса D
Задачи к разд. 23.1–23.4
Вычислить двойные интегралы:
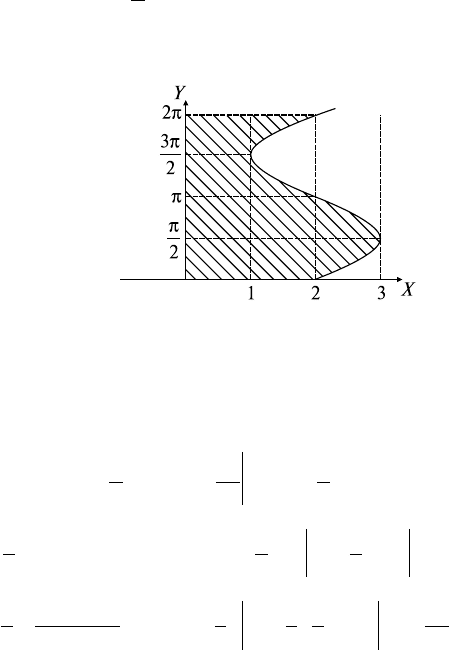
Задача 1.
Ixyxy
D
=-
∫∫
(),dd
∂D: y = x
2
+ x - 2, y = x + 2.
Решение: а) построим область D. Пер-
вая линия — парабола с вершиной в точ-
ке (-1/2; -9/4), проходящая через точки
(-2; 0), (1; 0).
Вторая линия — прямая. Решая со-
вместно данные уравнения, найдем ко-
ординаты точек пересечения:
х
2
+ x - 2 = х + 2 ⇒ x
2
- 4 = 0 ⇒
⇒ x = ±2 ⇒ А(-2; 0), В(2; 4)
(рис. 23.1).
Область D является правильной в на-
правлении оси ОУ, так как любая прямая,
параллельная данной оси, проходящая
Рис. 23.1
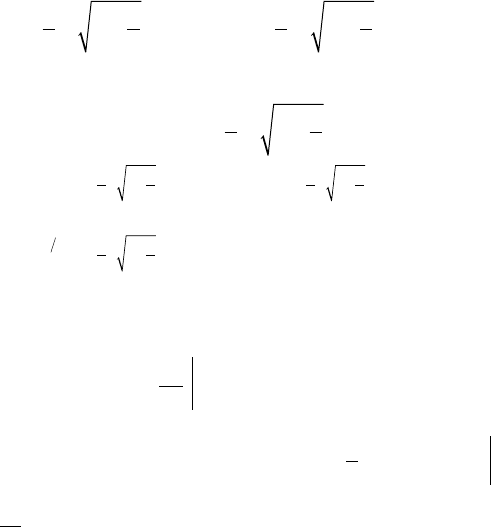
225
через внутренние точки области, пересекает границу ∂D только в
двух точках;
б) для данной области -2 ≤ х ≤ 2. Снизу область ограничена
параболой у = х
2
+ x - 2, сверху — прямой у = х + 2. Пользуясь
формулой
fxys xfxy y
Da
b
x
x
(, )(,) ,
()
()
dd d
∫∫ ∫∫
=
ϕ
ϕ
1
2
получим
Ix xyy
xx
x
=-
-
+-
+
∫∫
dd
2
2
2
2
2
().
При вычислении интеграла по формуле
fxys yfxy x
Dc
d
x
x
(, )(,)
()
()
dd d
∫∫ ∫∫
=
ψ
ψ
1
2
область D пришлось бы разбить на две части D
1
и D
2
с границами
∂D
1
и ∂D
2
соответственно:
∂=-- +Dx y
1
1
2
9
4
:
(слева),
xy=- ++
1
2
9
4
(справа),
-9/4 ≤ у ≤ 0;
∂D
2
: x = y - 2 (слева),
xy=- ++
1
2
9
4
(справа), 0 ≤ у ≤ 4.
Тогда
Iy xyxy xyx
y
y
y
y
=-+-
-
-- +
-+ +
-
-+ +
∫∫ ∫∫
dddd
94
0
1
2
9
4
1
2
9
4
0
4
2
1
2
9
4
() ()..
В данном
случае удобнее пользоваться первой формулой;
в) вычисляем внутренний интеграл (х считается постоян-
ным):
()() ,
(,
xyyxy
y
xxx
I
xx
x
xx
x
-=-=---⇒
⇒=
+-
+
+-
+
∫
d
2
2
2
2
2
2
2
42
2
05 244
05
xxxxx xxxx
42
2
2
532
2
2
24401
2
3
24
20
4
15
---= ---=
=-
-
-
∫
)(,)
.
d
226
Задача 2.
I
x
xy
D
=
∫∫
2
dd,
∂D: x = 2 + siny, x = 0, y = 0, y = 2π.
Решение: а) строим область D (рис. 23.2);
б) область D является правильной только в направлении OX,
поэтому переходим к повторному интегралу, пользуясь формулой
ОК, разд. 23.3:
Iy
x
xy
x
yy
y
y
===+ =
=
∫∫ ∫∫
+
+
dddd
0
2ππ π
24
1
4
2
1
0
2
0
2
2
0
2
2
0
2
sin
sin
(sin )
44
42
1
4
4
1
4
1
4
12
2
2
0
2
0
2
0
2
0
2
(sin sin) cos
cos
++ =⋅ -+
+
-
∫
yyyy y
y
y
d
d
πππ
ππππ
π
π
∫
=+ -⋅ =2
1
8
1
8
1
2
2
9
4
0
2
0
2
yysin.
Задача 3.
xxy
D
dd
∫∫
,
D: x
2
+ y
2
< 2x, y > 0.
Решение: а) строим область D. Это половина круга (x - 1)
2
+
+ y
2
= 1 (рис. 23.3), поэтому удобно перейти к полярной системе
координат.
Используем формулы x = rcosϕ, y = rsinϕ, тогда ∂D: r = 2cosϕ,
ϕ = 0 (0 ≤ ϕ ≤ π/2). Интеграл в полярной системе координат
примет вид (см. ОК, разд. 23.4):
Ir rr rr
DD
=⋅=
∫∫ ∫∫
coscos .ϕϕ ϕϕdd dd
2
;
б) переходим к повторному интегралу (ОК, разд. 23.3):
Рис. 23.2
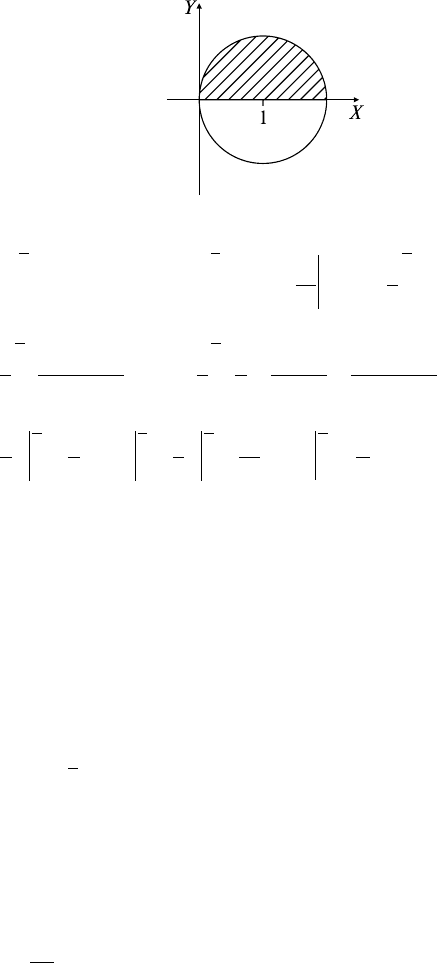
227
Irr
r
====
∫∫ ∫∫
ddddϕϕϕϕ ϕϕ
π
ϕ
π
ϕ
π
0
2
2
0
2
0
2
3
0
2
4
0
2
3
8
3
coscos cos
cos
cos
==
+
=+ +
+
∫∫
8
3
12
2
8
3
1
4
2
2
14
8
2
0
2
0
2
coscos cosϕ
ϕ
ϕϕ
ϕ
ππ
dd==
=+ ++ =
2
3
2
3
2
1
3
1
12
4
2
0
2
0
2
0
2
0
2
ϕϕϕϕ
π
ππππ
sinsin .
Задачи для самостоятельного решения
Вычислить интегралы:
1)
(),yxy
x
D
+
∫∫
edd
D — четырехугольник АВСD: A(2; 1), B(3; 1),
C(2; 4), D(3; 4).
2)
()xxy
D
-
∫∫
2d d:
а) ∂D: y = x, y = 3x, x = 1; б) ∂D: y = x,
y = 3x, y = 1.
3) а)
edd
x
y
D
xy
∫∫
,
∂D: x = y
2
, x = 0, y = 1; б)
cos( ),xyxy
D
+
∫∫
dd
∂D: x = 0, y = x, y = π.
4) а)
(),xyxy
D
+
∫∫
2dd
∂D: y = x
2
, y = 5x - 6; б)
(),2xyxy
D
-
∫∫
dd
∂D: y
2
= 4 - x, y
2
= x.
5)
x
y
xy
D
2
2
dd
∫∫
,
∂D: yx = 1, y = x, x = 2.
Рис. 23.3

228
6)
2xy xy
D
dd
∫∫
,
D — треугольник ABC с вершинами A(1; 1),
B(3; 3), C(2; -2).
7)
(),xyxy
D
-
∫∫
dd
D: x
2
+ y
2
< 9, x > 0, y > 0.
8)
1
22
--
∫∫
xyxy
D
dd,
D: x
2
+ y
2
< 1, x < y, x > -y.
9)
xxy
D
dd
∫∫
,
∂D: x
2
+ y
2
= 4y.
10)
ddxy
xy
D
22
1++
∫∫
,
∂D:
yx=-1
2
,
y = 0.
11)
yxy
D
dd
∫∫
,
∂D: x
2
+ y
2
= -2x, x
2
+ y
2
= -4x, y = 0 (y ≥ 0).
12)
sin
,
xy
xy
xy
D
22
22
+
+
∫∫
dd
∂D:
xy
22
2
9
+=
π
,
x
2
+ y
2
= π
2
.
13)
xxy
D
dd
∫∫
,
∂D: x
2
+ y
2
= 2x, x
2
+ y
2
= 2y.
Изменить порядок интегрирования:
14)
ddxfxy y
x
x
0
1
3
2
∫∫
(, );
15)
ddxfxy y
x
x
0
38
∫∫
(, );
16)
ddxfxy y
x
-
-
∫∫
2
2
0
4
2
(, );
17)
ddddyfxy xyfxyx
yy
-
-
-+
-
--
∫∫ ∫∫
+
2
1
2
0
1
00
(, )(,) ;
18)
ddddyfxy xyfxyx
y
y
0
10
1
2
0
2
2
∫∫ ∫∫
-
-
+(, )(,) ;
ddddyfxy xyfxyx
y
y
0
10
1
2
0
2
2
∫∫ ∫∫
-
-
+(, )(,) ;
19)
ddddxfxy yxfxyy
x
x
-
-
--
-
∫∫ ∫∫
+
2
1
2
0
1
00
2
(, )(,) .
Задачи к разд. 23.5
Задача 1. ∂D: y = x
2
- 1, y = 2. Найти S
D
.
Решение: а) строим область D (рис. 23.4);
б) площадь вычисляется по формуле (см. ОК, разд. 23.2, свой-
ство 4
0
)
Sxy
D
=
∫∫
dd,
причем удобнее в силу симметрии вычислить
1
2
S.
Переходим к повторному интегралу:
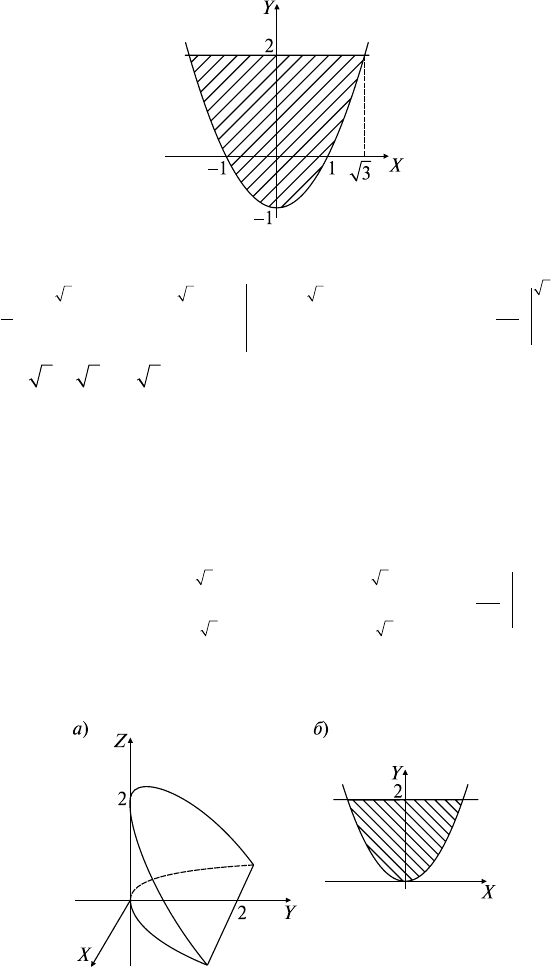
229
Рис. 23.4
1
2
33
3
0
3
1
2
0
3
1
2
2
0
3
3
0
3
2
2
Sxyxyxxx
x
x
x
==⋅=-=-
=
∫∫ ∫∫
-
-
dd dd()
==-=33 323.
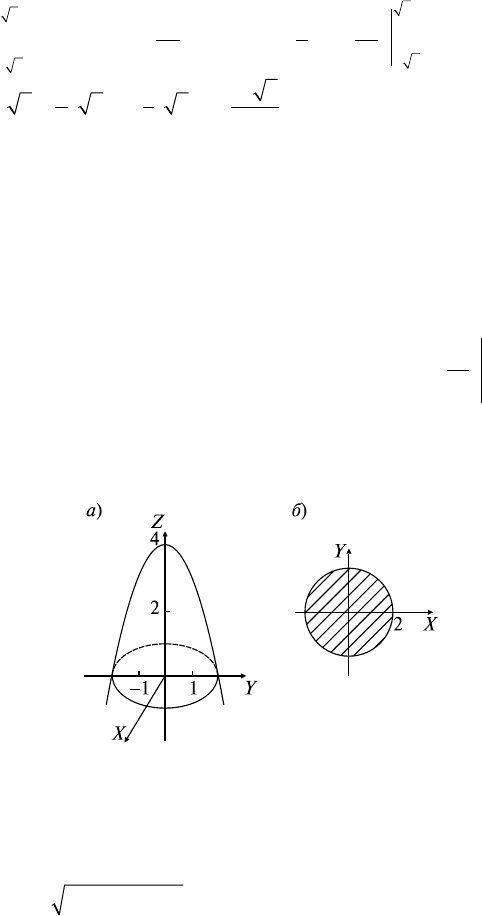
Задача 2. ∂Ω: y + z = 2, y = x
2
, z = 0. Найти V
Ω
.
Решение: Имеем цилиндрическое тело с накрывающей z = 2 - y
плоскостью и боковой цилиндрической поверхностью y = x
2
(рис. 23.5, а) Основанием его D является проекция тела на плос-
кость z = 0, т.е. ∂D: y = x
2
, y = 2 (рис. 23.5, б).
По формуле ОК, разд. 23.1
Vyxy xyyxy
y
D
x
x
=- =-=-
=
∫∫ ∫∫ ∫
--
() ()222
2
2
22
2
2
2
2
2
2
dd ddd
Рис. 23.5
230
=--+
=-+
=
-
-
∫
422
2
2
2
310
2
4
2
2
3
5
2
2
x
x
xxx
x
d
=- +=42
4
3
2
1
5
2
32 2
15
35
() () .
Задача 3. ∂Ω: z = 4 - x
2
- y
2
, z = 0. Найти V
Ω
.
Решение: Имеем цилиндрическое тело Ω с накрывающей
z = 4 - x
2
- y
2
(рис. 23.6, а), проекция D на плоскость z = 0 —
круг с границей ∂D: x
2
+ y
2
= 4 (рис. 23.6, б). Для вычисления
Vxyxy
D
=--
∫∫
()4
22
dd
переходим к полярной системе координат,
в которой ∂D: r = 2:
Vrrr rrrr
r
D
=- =-=-
=
∫∫ ∫∫ ∫
() ()442
4
2
0
2
2
0
2
2
4
0
2
0
2
dd dd dϕϕ ϕ
ππ
===
∫
48
0
2
dϕπ
π
.
Задача 4. Вычислить площадь σ поверхности G: z = x
2
+ y
2
,
0 ≤ z ≤ 9.
Решение: Так как z′
x
= 2x, z′
y
= 2y, то по формуле ОК, разд. 23.5,
п. 1,
σ= ++
∫∫
14 4
22
xyxy
D
dd
(рис. 23.7, а). Проекция D поверхно-
сти G на плоскость XOY — круг с границей x
2
+ y
2
= 9 (рис. 23.7,
б). Переходя к полярным координатам, получим
Рис. 23.6
