Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Нуриева С.Н., Дегтярева О.М. Математика в примерах и задачах
Подождите немного. Документ загружается.


251
Задачи для самостоятельного решения
Вычислить криволинейные интегралы:
1)
() ,xy yxxy
L
-+
∫
2
dd
где L: у = 2х
2
от т. А(0; 0) до т. В(1; 2);
2)
2
2
xy xxy
L
dd
∫
+ ,
где L: а) отрезок прямой АВ; б) y = x
2
;
в) x = y
2
; г) y = x
3
от А(0; 0), В(1; 1);
3)
()(),32
22
xyxx yy
L
++-
∫
dd
где L: ломаная АВСА: А(0; 0),
В(1; 0), С(0; 1);
4)
xy x
L
d
∫
,
где L — дуга синусоиды y = sinx от х = 0 до х = π;
5)
yx zy xz
L
ddd
∫
++,
если: а) L — ломаная ОАВС: О(0; 0; 0),
А(1; 0; 0), В(1; 1; 0), С(1; 1; 1); б) L — отрезок прямой ОС;
6)
ed d
xy
L
xyy
+
∫
+ ,
где L — ломаная ОАВ: О(0; 0), А(4; 0),
В(0; 2);
7)
xx xy y
L
2
dd
∫
+ ,
где L — дуга окружности x = cost, y = sint,
0 ≤ t ≤ π/2;
8)
xy yx
xy
22
53 53
dd-
+
∫
,
где L — часть астроиды х = аcos
3
t, y = asin
3
t,
0 ≤ t ≤ π/2;
9)
()()(),yzxzxy xyz
L
-+-+-
∫
ddd
где L — виток винтовой ли-
нии x = 2cost, y = 2sint, z = 3t, 0 ≤ t ≤ 2π.
10) Найти работу, совершаемую силой F{y, -x}вдоль эллипса
x = acost, y = bsint, 0 ≤ t ≤ 2π.
Задачи к разд. 26.5
Задача 1. Используя формулу Грина, вычислить криволинейный
интеграл
(sin())( sin( )) ,xyxxyx xy yxyy
L
3233 233
22-+ ++++
∫
dd
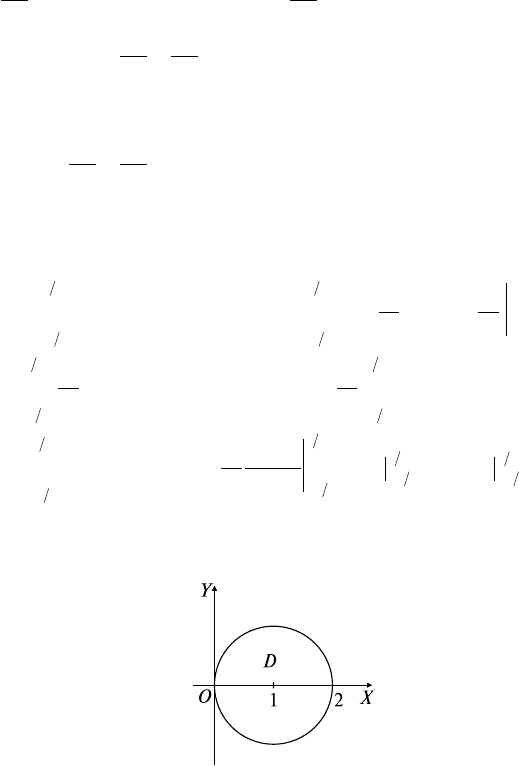
где L — окружность х
2
+ у
2
= 2х, пробегаемая против хода часовой
стрелки.
252
Решение: С помощью элементарных преобразований приведем
уравнение окружности х
2
+ у
2
= 2х к виду (х - 1)
2
+ у
2
= 1. От-
сюда следует, что центр окружности находится в точке С(1; 0),
а радиус равен 1 (рис. 26.2). Для нашего интеграла
Р(х, у) = х
3
- 2у + х
2
sin(x
3
+ y
3
), Q(x, y) = 2xy +
+ y
2
sin(x
3
+ y
3
),
тогда
∂
∂
=- ++⋅
∂
∂
=+ +⋅
P
y
xxyy
Q
x
yy xy x2323
2332 2332
cos( ), cos( ),
следовательно,
∂
∂
-
∂
∂
=+
Q
x
P
y
y22.
Для вычисления исходного интеграла используем формулу
Грина
I
Q
x
P
y
xy xxy
DD
=
∂
∂
-
∂
∂
=+
∫∫ ∫∫
dd dd().22
Так как область D — круг, перейдем к полярным координатам:
х = rcosϕ, у = rsinϕ, dxdy = rdrdϕ. Уравнение заданной окруж-
ности в полярной системе координат имеет вид r = 2cosϕ. Тогда
Irrr
rr
=+=+
--
∫∫ ∫
dddϕϕ ϕϕ
π
π
ϕ
π
π
2
2
0
2
2
2
32
0
2
22 2
3
2
2
(sin )[sin]
cos
co
ss
(cos sincos )cos cos
ϕ
π
π
π
π
ϕϕ ϕϕ ϕϕ
=
=+=- +
+
--
∫∫
16
3
4
16
3
2
32
2
2
3
2
2
dd
((cos )
cos
sin.12
16
34
222
2
2
4
2
2
2
2
2
2
+=-++=
-
-
--
∫
ϕϕ
ϕ
ϕϕπ
π
π
π
π
π
π
π
π
d
Рис. 26.2
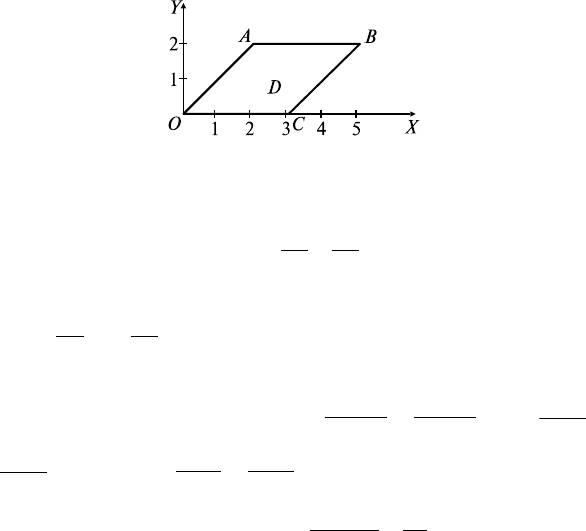
253
Задача 2. Вычислить криволинейный интеграл
()(),
coscos
22
x
L
y
xy xxyy++-
∫
dd
где L — контур четырехугольника с вершинами О(0; 0), А(2; 2),
В(5; 2), С(3; 0), указанными в порядке обхода (рис. 26.3).
Рис. 26.3
Решение: Так как обход контура интегрирования проводится в
отрицательном направлении, то формула Грина имеет вид
Pxyx Qxyy
Q
x
P
y
xy
LD
(, )(,) .dd dd
∫∫∫
+=-
∂
∂
-
∂
∂
В нашем случае Р(х, у) = 2
cosx
+ xy, Q = 2
cosy
- xy. Следова-
тельно,
∂
∂
=
∂
∂
=-
P
y
x
Q
x
y,
и
Ixyxyxyxy
DD
=- -- =+
∫∫ ∫∫
() ().dd dd
Находим уравнения ОА и СВ как уравнения прямых, проходя-
щих через две заданные точки:
xx
xx
yy
yy
-
-
=
-
-
1
21
1
21
;
OA:
xy
xy
-
-
=
-
-
⇒=
2
02
2
02
;
xy
xy
-
-
=
-
-
⇒=
2
02
2
02
;
CB:
xy
xy
-
-
=
-
-
⇒=+
5
35
2
02
3.
Значит
Iyxyx
yy
yy
y
y
=+=
+
-+
=
∫∫ ∫
+
dd d
0
2
3
22
0
2
3
22
321()
()
.
Задачи для самостоятельного решения
Вычислить с помощью формулы Грина:
11)
xy yxyx
L
22
dd
∫
- ,
где L — окружность x
2
+ y
2
= a
2
;
12)
() ,22
2
xy xx xy
L
-+
∫
dd
L — контур фигуры, ограниченной
линиями у = 2х
2
, у = 4;
13)
yx xy y
L
22
dd
∫
++(),
L — контур треугольника АВС с верши-
нами А(2; 0), В(2; 2), С(0; 2);
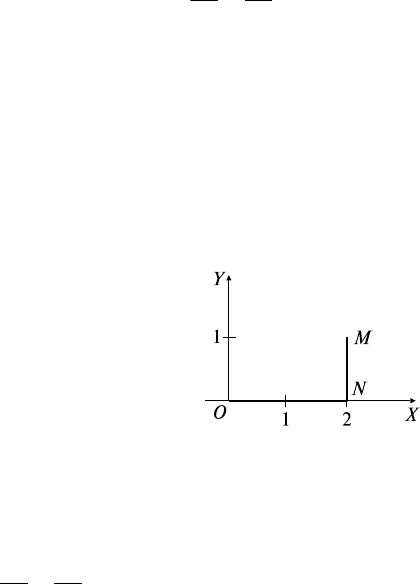
254
14)
()(),xy xx xy xy y
L
23 32
++ +
∫
dd
где L — контур фигуры, огра-
ниченной линиями y = x
2
, y = 1, x = 0, пробегаемый в положи-
тельном направлении;
15)
edd
-+
∫
+
xy
L
xy xxyy
22
22
(cos() sin( )),
где L: х
2
+ у
2
= R
2
.
Задачи к разд. 26.6–26.8
Задача 1. Вычислить
2
00
21
2
xy xxydd
(;)
(;)
.
∫
+
Решение: Так как
∂
∂
=
∂
∂
=
P
y
Q
x
x2 ,
то криволинейный интеграл не
зависит от пути интегрирования. В качестве пути интегрирования,
связывающего точки (0; 0) и (2; 1), возьмем ломаную ONM
(рис. 26.4).
ON: у = 0, dу = 0, 0 ≤ х ≤ 2; NM: х = 2, dх = 0, 0 ≤ у ≤ 1.
Следовательно,
2024
00
21
22
0
1
xy xxyydd d
(;)
(;)
∫∫
+=+=
(на звене ОN ломаной подынтегральное выражение равно нулю).
Рис. 26.4
Задача 2. Найти первообразную функцию U(х, у), если dU =
= (у + ln(х + 1))dx + (х + 1 - е
у
)dу.
Решение: Имеем Р(х, у) = у + ln(х + 1), Q(х, у) = х + 1 - е
у
,
∂
∂
=
∂
∂
=
P
y
Q
x
1.
Пусть х
0
= 0, у
0
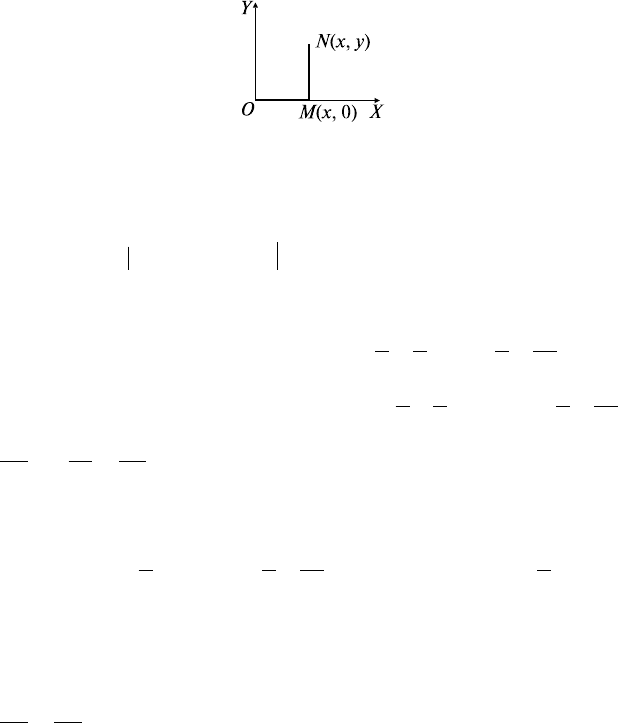
= 0 и контуром L является ломаная ОMN
(рис. 26.5). Тогда
255
Uxyxxx yc xx x
x
x
y
y
(, )ln( )( )(ln()
ln())
=+++-+=+-+
++
∫∫
11 1
1
00
0
ded
xx
y
y
y
xy ycxxxxy
yc
++-+=+ +-++
+- ++
()()ln()
.
e
e
0
11
1
Задача 3. Найти U(х, у), если
dddU
xy
x
y
x
y
y=+
+-
11 2
2
.
Решение: В этом случае
Pxy
xy
(, ),=+
11
Qxy
y
x
y
(, ),=-
2
2
∂
∂
=- =
∂
∂
P
y
y
Q
x
1
2
.
В качестве начальной точки (х
0
, у
0
) возьмем, например,
т. А(1; 1). Тогда
Uxy
x
x
y
x
y
yc xy
x
y
c
x
y
(, )lnln=+
+-
+= ++-+
∫∫
1
1
2
21
1
2
1
dd ..
Задача 4. Решить дифференциальное уравнение (4х
3
у
3
-
- 3у
2
+ 8)dх + (3х
4
у
2
- 6ху - 1)dу = 0.
Решение: Р(х, у) = 4х
3
у
3
- 3у
2
+ 8, Q(х, у) = 3х
4
у
2
- 6ху - 1,
∂
∂
=
∂
∂
=-
P
y
Q
x
xy y12 6
32
.
Следовательно, Рdх + Qdу = dU. Таким образом, dU = 0 ⇒
⇒ U = c. Пусть (х
0
, у
0
) = (0; 0). Тогда
Uxxy xy yc
x
y
=+ -- =
∫∫
8361
0
42
0
dd(),
т.е. 8x + x
4
y
3
- 3xy
2
- y = c.
Рис. 26.5
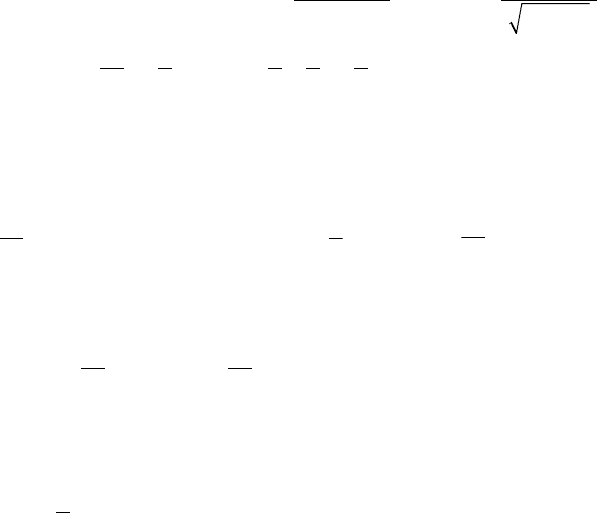
256
Задачи для самостоятельного решения
Вычислить криволинейные интегралы:
16)
xy yxdd
(,)
(,)
;
-
∫
+
12
23
17)
yx xy
x
dd-
∫
2
21
12
(,)
(, )
;
18)
xx yy
xy
dd+
+
∫
22
10
68
(, )
(,)
;
19)
1
2
2
1
2
-
++
∫
y
x
y
x
x
y
x
y
x
y
x
ycossin cos;
(, )
(,)
dd
π
π
20)
ed ed
2
10
21
2
21
yy
xx y
(, )
(,)
().
∫
++
+ (2xe
2y
+ 1)dy.
Установить существование первообразной u(х, у) и найти ее для
дифференциальных выражений:
21) (4x
3
y
3
- 3y
2
+ 5)dх + (3х
4
y
2
- 6xу - 4)dу; 22) (3х
2
y -
-
y
3
3
)dх + (x
3
- xу
2
)dу; 23) (3х
2
y +
1
y
)dх + (x
2
-
x
y
2
)dу.
Найти первообразную функцию u(x, y) по ее полному диффе-
ренциалу:
24) du = (e
2y
- 5y
3
e
x
)dx + (2xe
2y
- 15y
2
e
x
)dy; 25) du =
=+
+-
12
1
4
2
2
2
3
3
xy
y
xx
x
y
ydd;
26) du = (e
x+y
+ cos(x - y))dx +
+ (e
x+y
- cos(x - y) + 2)dy.
Решить дифференциальные уравнения:
27) (3x
2
y + 1)dx + (x
3
- 1)dy = 0; 28)
(ln)2
2
xy yx
x
ed++
+++
=eed
xy
x
y
y
2
0;
29) (x + y + 1)(e
x
- e
y
)dx + (e
x
- (x + y +
+ 1)e
y
)dy = 0.
257
27. Поверхностные интеГралы
опорный конспект № 27
27.1. Поверхности в R
3
G: z = z(x, y), М(x, y) ∈ R
2
, z(x, y), z ′
x
, z′
y
— непрерывны в
D ⇔ G — гладкая поверхность, являющаяся двусторонней.
Единичный вектор нормали
n
= {cosα, cosβ, cos γ},
α=(, ),
ni
β
= (, ),
nj
γ=(, ),
nk
n
(M) — непрерывная функция т. М
27.2. Пи Iр
1. Определение ПИ Iр
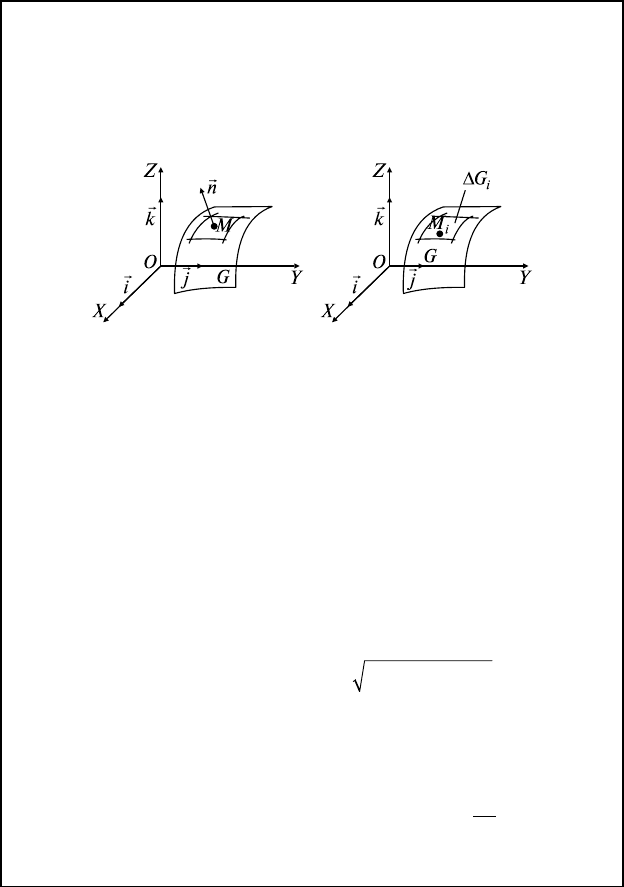
f(x, y, z) непрерывна в Ω, G ⊂ Ω, G
i
∩ G
j
= ∅,
GG
i
i
n
=
=
∆
1
∪
,
∆σ
i
— площадь ∆G
i
,
MGfxyz f
ii ii i
G
iiii
i
n
(, ,) (, ,) lim((, ,) )ξηζσξηζσ
λ
∈⇒ =
∫∫
∑
→
=
∆∆d
0
1
,,
λ = maxdiam∆G
i
, µ(M) — поверхностная плотность G ⇒ m =
=
∫∫
µσ(, ,)xyz
G
d
— масса G
2. Вычисление ПИ Iр
G: z = z(x, y), (x, y) ∈ D — гладкая поверхность ⇒
⇒= +
′
+
′
∫∫ ∫∫
fxyz fxyzxy zz
GD
xy
(, ,) (, ,(,))()()ddσσ1
22
27.3. Пи IIр
1. Определение ПИ IIр
P(x, y, z), Q(x, y, z), R(x, y, z) непрерывны в Ω ⊂ R
3
,
G ⊂ Ω — двусторонняя ориентированная поверхность, ∆D
i
xy
=
= пр
XOY
∆G
i
, ∆D
i
xz
= пр
XOZ
∆G
i
, ∆D
i
yz
= пр
YOZ
∆G
i
,
in= 1,;
∆S
i
xy
, ∆S
i
yz
,
∆S
i
xz
— (±) площади ∆D
i
xy
, ∆D
i
yz
, ∆D
i
xz
; M
i
(ξ
i
, η
i
, ζ
i
) ∈ ∆G
i
⇒

258
⇒++=
∫∫
PyzQxz Ryx
G
dd dd dd
=++
→
=
∑
lim()()().
λ 0
1
PM SQMS RM S
ii
yz
i
n
ii
xz
ii
yx
∆∆∆
Связь ПИ Iр и ПИ IIр:
PyzQxz RyxP QR
GG
dd dd dd d
∫∫ ∫∫
++=++(cos coscos )αβγσ
v
(x, y, z) = {P, Q, R} — скорость жидкости, протекающей че-
рез G ⇒ поток жидкости
Π
G
GG
PyzQxz Ryxvn=++=⋅
∫∫ ∫∫
dd dd dd d
σ
2. Вычисление ПИ IIр
D
xy
= пр
XOY
G, D
xz
= пр
XOZ
G, D
yz
= пр
YOZ
G,
G: z = z(x, y) ∨ y = y(x, z) ∨ x = x(y, z) ⇒
⇒++=±±
±
∫∫ ∫∫
PyzQxz RxyPxyzyzyz
Qxyxz
GD
yz
dd dd dd dd((,),,)
(, (,), zzxzRxyzxyxy
DD
xz xy
)(,,(, )) ,dd dd
∫∫ ∫∫
±
где (+) — для острых углов
(,),
ni
(, ),
nj
(, ),
nk
; (-) — для тупых
27.4. Фомула Остроградского—Гаусса
P(M), Q(M), R(M) — непрерывны вместе с частными производны-
ми в Ω, ∂Ω = G — ориентированная поверхность ⇒
PyzQxz Rxy
P
x
Q
y
R
z
xyz
G
dd dd dd
ddd
∫∫
∫∫∫
++=
=
∂
∂
+
∂
∂
+
∂
∂
Ω
259
27.5. Формула Стокса
P(M), Q(M), R(M) — непрерывные вмес-
те с частными производными на ориен-
тированной поверхности G, L = ∂G —
гладкая ⇒
Px Qy Rz
Q
x
P
y
xy
R
y
Q
z
yz
LG
ddddd
dd
∫∫∫
++=
∂
∂
-
∂
∂
+
+
∂
∂
-
∂
∂
++
∂
∂
-
∂
∂
P
z
R
x
xzdd
Задачи к разд. 27
Задача 1. Вычислить
Jzxy
G
=++
∫∫
2
4
3
dσ,
где G:
xyz
234
1++=
(x ≥ 0, y ≥ 0, z ≥ 0).
Решение: Так как
z
xy
=--
41
23
,
z′
x
= -2,
′
=-z
y
4
3
,
то по фор-
муле ОК, разд. 27.2, п. 2,
J
xy
xy xy
D
=--
++
+- +-
=
=
∫∫
41
23
2
4
3
12
4
3
46
2
2
() dd
11
3
ddxy
D
∫∫
.
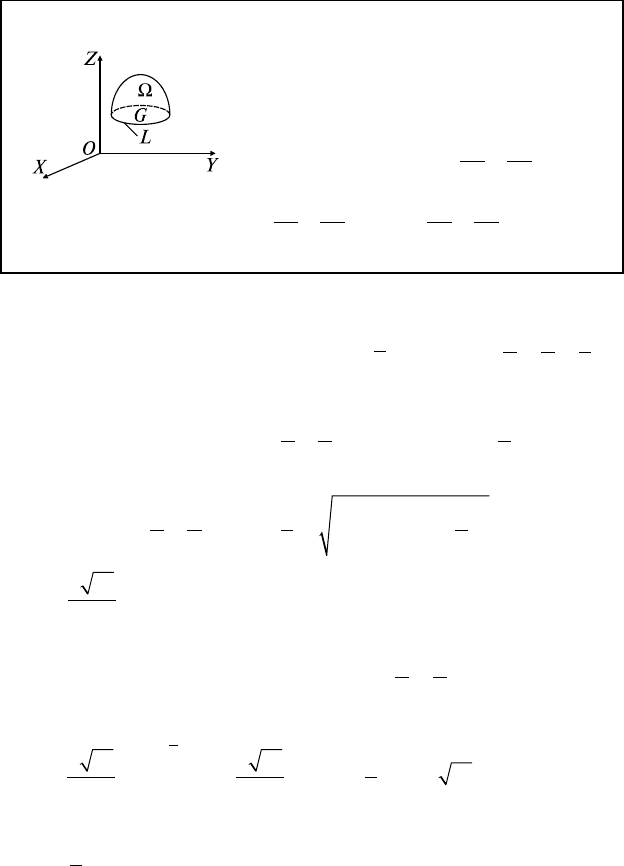
Граница области D — проекции плоскости G на плоскость XOY —
треугольник с границей ∂D: x = 0, y = 0,
xy
23
1+=
(рис. 27.1).
Переходим к повторному интегралу:
Jxyxx
x
==-
=
∫∫ ∫
-
461
3
461
3
3
3
2
461
0
2
0
3
3
2
0
2
dd d .
Двойной интеграл можно вычислить проще, так как
ddxy
D
∫∫
=
==⋅⋅=S
D
1
2
23 3.
Задача 2. Вычислить
Ixyz yxzzxy
G
=++
∫∫
dd dd dd
,
где G —
внешняя сторона куба, составленного плоскостями x = 0, y = 0,
z = 0, x = 1, y = 1, z = 1.

260
Решение: 1-й способ. Пользуясь свойством аддитивности интег-
ралов, разобьем интеграл I на сумму шести слагаемых по каждой
грани куба:
I = I
1
(x = 0) + I
2
(y = 0) + I
3
(z = 0) + I
4
(x = 1) + I
5
(y = 1) +
+ I
6
(z = 1).
Рассмотрим каждое слагаемое, пользуясь ОК, разд. 27.3, п. 2:
Ixyz yxzzxy yz
Gx D
yz
1
0
1
0000=++=-⋅ --=
=
∫∫ ∫∫
dd dd dd dd
()
,
где учтено, что нормаль к поверхности x = 0 составляет тупой угол
с осью ОX (знак минус перед интегралом) и что слагаемые y dxdz и
zdxdy равны нулю, так как на грани х = 0 они при проектировании
не дают области (рис. 27.2).
Аналогично I
2
= I
3
= 0.
Ix xyzyxz zxyyz
GD
xyz
4
1100
41
() ,
()
== ++=+ ⋅++
=
∫∫ ∫∫
dd dd dd dd
где D
yz
— единичный квадрат на плоскости YOZ и учтено, что нор-
маль к поверхности x = 1 составляет острый угол с осью OX.
Рис. 27.2
Рис. 27.1
