Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Нуриева С.Н., Дегтярева О.М. Математика в примерах и задачах
Подождите немного. Документ загружается.

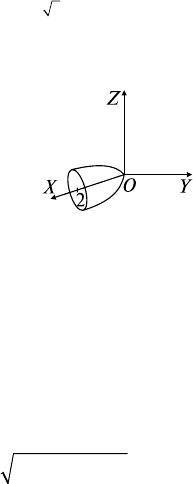
261
Так как
ddyz
D
yz
∫∫
— площадь области D
yz
, т.е. квадрата с длиной
стороны, равной 1, то I
4
= 1. Аналогично I
5
= I
6
= 1. Окончатель-
но I = 3.
2-й способ. По формуле Остроградского—Гаусса (ОК, разд. 27.4)
имеем
Ixyz xyz===
∫∫∫ ∫∫∫
33
0
1
0
1
0
1
dddddd
Ω
.
Задача 3. Вычислить
Ixyz
G
=
∫∫
dd,
где G — внешняя сторона
части параболоида x = y
2
+ z
2
, отсеченная плоскостью x = 2.
Решение: По формуле ОК, разд. 27.3, п. 2, имеем
Iyzyz
D
yz
=+
∫∫
(),
22
dd
где D
yz
: y
2
+ z
2
= 2 (рис. 27.3).
Переходим к полярным координатам:
Irrr rr
D
yz
====
∫∫ ∫∫ ∫
2
0
2
3
0
2
0
2
24dd dd dϕϕ ϕπ
ππ
.
Рис. 27.3
Задачи для самостоятельного решения
Вычислить поверхностные интегралы I рода:
1)
xyz
G
dσ
∫∫
,
G: x + y + z = 1 (x ≥ 0, y ≥ 0, z ≥ 0);
2)
x
G
dσ
∫∫
,
G: x
2
+ y
2
+ z
2
= R
2
(x ≥ 0, y ≥ 0, z ≥ 0);
3)
y
G
dσ
∫∫
,
G:
zRxy=--
222
.

262
Вычислить поверхностные интегралы II рода:
4)
xyzxy
G
22
dd
∫∫
,
G: x
2
+ y
2
+ z
2
= R
2
(z ≤ 0, внешняя сторо-
на);
5)
xyzyxz zxy
G
dd dd dd
∫∫
++,
G: x + y + z = а (верхняя сторо-
на в I октанте);
6)
zxy
G
dd
∫∫
,
G:
x
a
y
b
z
c
2
2
2
2
2
2
1++=
(внешняя сторона);
7)
xz xy xyyz yz xz
G
dd dd dd
∫∫
++,
G: x = y = z = 0, x + y + z =
= 1(внешняя сторона);
8)
yz xy xz yz xy xz
G
dd dd dd
∫∫
++,
G: x = y = z = 0, z = H, x
2
+
+ y
2
= R
2
(в I октанте, внешняя сторона).
28. скалЯрное и векторное ПолЯ
опорный конспект № 28
28.1. Скалярное поле (СП)
1. Определение СП. Линии и поверхности уровня СП
u(M), M(x, y) ∈ D ⊆ R
2
или M(x, y, z) ∈ Ω ⊆ R
3
u(x, y) = c, c = const — линии уровня,
u(x, y, z) = c — поверхности уровня
2. Производная по направлению СП
l = {cos ,cos ,cos }||αβγ
прямой L, т. М, M
1
∈ L ⇒
∂
∂
=
-
=
∂
∂
+
∂
∂
+
∂
∂
→
u
l
uM uM
MM
u
x
u
y
u
z
MM
lim
() ()
coscos cos
1
1
1
αβγ
3. Градиент СП
О:
gradu
u
x
i
u
y
j
u
z
ku=
∂
∂
+
∂
∂
+
∂
∂
=∇
Т:
∂
∂
=⋅
u
l
ulgrad
,
(grad)u
M
0
направлен по нормали к поверхно-
сти уровня u(x, y, z) = c

263
28.2. Векторное поле (ВП)
1. Определение ВП. Векторные линии
ВП:
vM vM vM vM
xyz
(){( ), (),()},=
M ∈ Ω ⊂ R
2
∨ M ∈ Ω ⊂ R
3
Векторные линии ВП
vM(),
M ∈ Ω — кривые L: касательные
к L в т. М совпадают с
vM(),
их уравнения
dddx
v
y
v
z
v
xyz
==
2. Поток и дивергенция ВП
О: Поток ВП
vM(),
M ∈ Ω:
Π
G
G
vM nM=⋅
∫∫
()()dσ
О: Дивергенция ВП
vM(),
M ∈ Ω:
div( )lim ,
vM
V
V
G
=
→0
Π
где M ∈ Ω* ⊂ Ω,
G = ∂Ω*, V — объем Ω*
Т:
div( )()
vM
v
x
v
y
v
z
vM
x
y
z
=
∂
∂
+
∂
∂
+
∂
∂
=∇
Векторная запись формулы Остроградского—Гаусса:
vM nM vM v
G
()() div( )
∫∫ ∫∫∫
⋅=ddσ
Ω
3. Циркуляция и ротор ВП
О: Циркуляция
vM(),
M ∈ Ω, по L:
Цdddd
L
L
x
L
yz
vM rvxvyvz==++
∫∫
()
O: Ротор
vM(),
M ∈ Ω:
rot( )()
vM vM
ijk
xyz
vvv
xyz
=∇×=
∂
∂
∂
∂
∂
∂
Векторная запись формулы Стокса:
Цd d
L
LG
vM rvMnM=⋅=⋅
∫∫∫
() rot( )() σ
264
4. Простейшие ВП
а) O: Трубчатое соленоидальное ВП ⇔
vM(),
MvM∈=Ω: div( );
0
б) O: Потенциальное (безвихревое) ВП ⇔
vM(),
MuMvMuM∈∃ =Ω,()()grad( );:
в) O: Гармоническое ВП ⇔
vM(),
MvMvM∈==Ω: rot( ),div( )
00
Для гармонического ВП ∃u(M): ∆u = 0,
где
∆=
∂
∂
+
∂
∂
+
∂
∂
2
2
2
2
2
2
xyz
— оператор Лапласа
Задачи к разд. 28.1
Задача 1. Найти
∂
∂
u
l
в точке M
0
(1; -1; 2) по направлению
l
:
a
= {2; -1; 0}, если u = 2x
3
yz + x
2
+ y
3
+ z
3
.
Решение: Воспользуемся формулой ОК, разд. 28.1, п. 2. Имеем
∂
∂
=+=- +=-
u
x
xyzx
M
M
0
0
62 12 210
2
() ,
∂
∂
=+ =+=
u
y
xz y
M
M
0
0
23 437
32
() ,
∂
∂
=+ =- +=
u
z
xy z
M
M
0
0
23 21210
32
() .
Находим направляющие косинусы вектора
a
:
cos
()
;cos ;cos .αβγ==
+- +
===
-
==
a
a
a
a
a
a
x
y
z
2
210
2
5
1
5
0
22
Следовательно, получаем
∂
∂
=- +-
+⋅=-
u
l
10
2
5
7
1
5
10 0
27 5
5
.
Задача 2. Найти величину наибольшей производной по направ-
лению в точке М
0
(1; 1; 2) скалярного поля u = x
2
y
2
z - ln(z - 1).
265
Решение: Так как
∂
∂
=⋅
u
l
ulgrad
(ОК, разд. 28.1, п. 3), то
∂
∂
=
u
l
u
наиб
grad .
Находим
(grad)u
M
0
по формуле (ОК, разд. 28.1,
п. 2. Имеем
∂
∂
==
u
x
xy z
M
M
0
0
24
2
() ,
∂
∂
==
u
y
xyz
M
M
0
0
24
22
(),
∂
∂
=-
-
=
u
z
xy
z
MM
00
22
1
1
0.
Тогда
(grad) ,uij
M
0
44=+
∂
∂
=+=
u
l
наиб
16 16 42.
Задачи для самостоятельного решения
Найти
∂
∂
u
l
в точке М
0
по направлению
l
:
1) а)
u
y
x
= arctg,
M
0
(1; 3),
l
:
ai j=+34;
б) u = xy
2
+ z
2
- xyz,
M
0
(1; -1; 2),
l
:
a
= {-2; 4; -1}.
Найти
∂
∂
u
l
в точке М
0
по направлению
MM
01
:
2) а)
uxyx
y
z
=++ln();
2
2
3
M
0
(1; -1; 2), М
1
(2; 1; 1); б) u =
=+e
x
xy z
3
2
2();
M
0
(0; 1; 1), M
1
(1; 1; 2).
Найти gradu в точке М
0
:
3) а)
uxy=++4
22
,
M
0
(2; 1); б) u = sin
2
(xy - 2xz + 3yz),
M
0
1
4
0;; .
π
4) Найти угол между градиентами скалярных полей u(x, y, z) и
v(x, y, z) в точке М:
u
xyz
=
1
,
v = x
2
+ 9y
2
+ 6z
2
,
M 1
1
3
1
6
;; .
5) Найти градиент скалярного поля потенциала
ϕ=
e
r
электро-
статического заряда e, помещенного в начале координат, если r —
расстояние от точки M(x, y, z) до заряда e.
6) Дано скалярное поле u = x
2
yz
2
- 4y. Найти направление и
величину наибольшей скорости изменения поля в т. М(3; 0; 4).
266
Задачи к разд. 28.2
Задача 1. Найти векторные линии векторного поля
vxiyjzk=-+2 .
vxiyjzk=-+2 .
Решение: По формуле ОК, разд. 28.2, п. 1, имеем дифференци-
альные уравнения векторных линий:
dddx
x
y
y
z
z2
=- =
или
dd
dd
dd
dd
x
x
y
y
x
x
z
z
x
x
y
y
c
x
x
z
z
c
2
2
2
2
1
=-
=
⇒
=- +
=+
∫∫
∫∫
,
,
ln ,
ln
22
.
Таким образом, получаем уравнения линий:
ln ln ,
ln ln ,
,
.
x
c
y
xcz
y
c
x
z
x
c
=
=
⇒
=
=
1
2
1
2
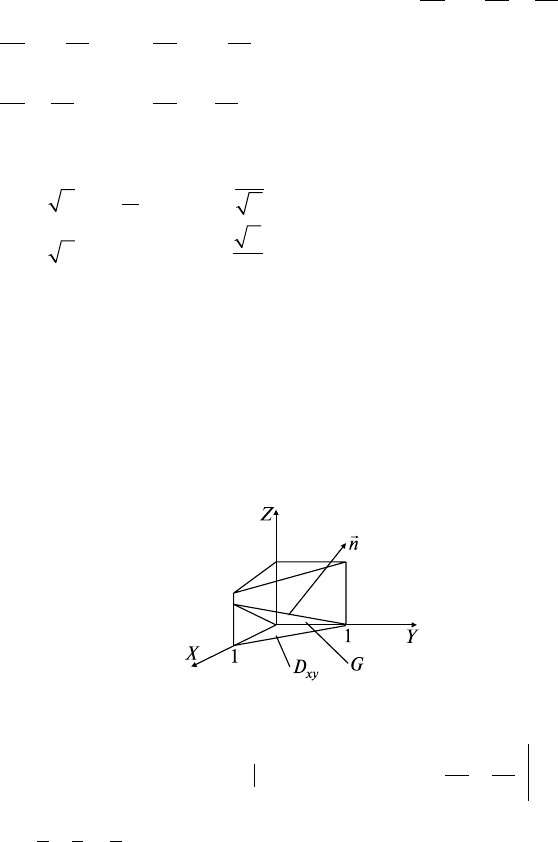
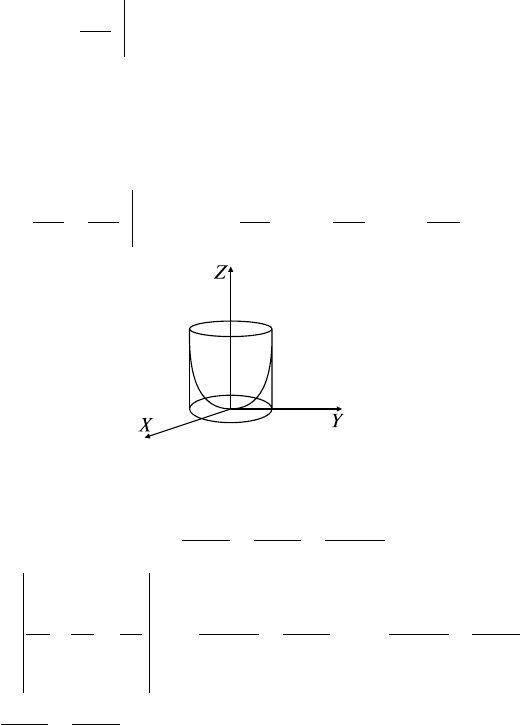
Задача 2. Найти поток векторного поля
v
= {0; 0; z} через часть
плоскости z = x, расположенную внутри цилиндра x = 0, y = 0,
x + y = 1, если угол между нормалью
n
к плоскости и осью OZ —
острый.
Решение: По формуле ОК, разд. 28.2, п. 2, используя для вычис-
ления ОК, разд. 27.2, п. 2, имеем
Π= =
∫∫ ∫∫
zxy xxy
GD
xy
dd dd,
где ∂D
xy
:
x = 0, y = 0, x + y = 1 (рис. 28.1).
Рис. 28.1
Переходим к повторному интегралу:
Π= =⋅=- =-
=
=
∫∫ ∫∫
-
-
dd ddxxyxxy xxx
xx
x
x
0
1
0
1
0
1
0
1
0
1
23
0
1
1
23
()
11
2
1
3
1
6
-=.
267
Задача 3. Найти поток векторного поля
vxyi xz jzk=- ++()3
222
через замкнутую поверхность G: z = x
2
+ y
2
, z = 0, x
2
+ y
2
= 4.
Решение: Найдем
div( )()()
vxyxzz z
xy z
=-
′
+
′
+
′
=+3438
22
и вос-
пользуемся векторной записью формулы Остроградского—
Гаусса:
Π
ΩΩ
==+= +=
∫∫∫ ∫∫∫ ∫∫ ∫
+
div()()
vV zxyz xy zz
xy
D
xy
dddd dd d
dd
38 38
0
22
DD
xy
D
z
z
xy xy xy
∫∫ ∫∫
+
=+++
+
3
8
2
34
2
0
22 222
22
(( )( )) .dd
Так как ∂D: x
2
+ y
2
= 4 (рис. 28.2), переходим к полярным ко-
ординатам:
Π= +=+=
=+
∫∫ ∫∫
∫
() ()34 34
3
4
4
6
24
0
2
35
0
2
0
2
46
rrrr rrr
rr
D
dd dd
d
ϕϕ
ϕ
π
π
=+
=⋅=
∫
0
2
0
2
12
128
3
164
3
2
328
3
dϕππ
π
.
Рис. 28.2
Задача 4. Вычислить дивергенцию и ротор векторного поля
v
= {xy, xz, -yz}.
Решение: Имеем
div
() () ()
.
v
xy
x
xz
y
yz
z
yy=
∂
∂
+
∂
∂
+
∂-
∂
=+-=00
rot
()() (
v
ijk
xy z
xy xz yz
i
yz
y
xz
z
j=
∂
∂
∂
∂
∂
∂
-
=
∂-
∂
-
∂
∂
-
∂
--
∂
-
∂
∂
+
+
∂
∂
-
∂
∂
=---
yz
x
xy
z
k
xz
x
xy
y
izxj
)()
() ()
()
(()()
()().
-- +-=
=- ++-
00
kz x
xzizxk
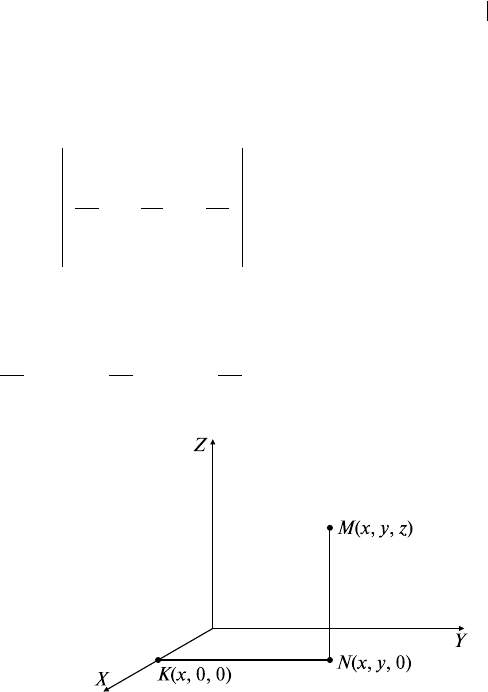
268
Следовательно, поле
v
является соленоидальным (ОК, разд. 28.2,
п. 4):
Задача 5. Найти циркуляцию векторного поля
v
= {y; -x; z}
вдоль окружности x = Rcost, y = Rsint, z = 1 (0 ≤ t ≤ 2π).
Решение: Используем определение циркуляции (см. ОК,
разд. 28.2, п. 3):
Цddd
dd
dd=-+=
==-
==
=
∫
yx xy zz
xR txRtt
yR tyRtt
z
L
cos, sin,
sin, cos,
110
0
2
2
0
d
dd
z
RtRtRtRttRt
=
=
--⋅=-
∫
,
(sin (sin )cos cos)
π 22
2
0
2
2
2
π
π
π
∫
=- =-Rt R .
Задача 6. Показать, что поле
vyzi xzjxyk=+ ++ ++()()()
потенциально, и найти его потенциал.
Решение: Находим
rot()( )().
v
ijk
xyz
yzxzxy
ijk=
∂
∂
∂
∂
∂
∂
+++
=---+-=11 11 11 0
Следовательно, поле
v
потенциально. Также
div
v =⇒0
поле
v
гармоническое.
Потенциал u(M) удовлетворяет условию grad u(M ) =
v
(M ),
т.е.
∂
∂
=+
∂
∂
=+
∂
∂
=+
u
x
yz
u
y
xz
u
z
xy,,,
du = (y + z)dx + (x + z)dy +
Рис. 28.3

269
+ (x + y)dz,
uyzx xzyxyz
xyz
=+++ ++
∫
()()().
(,,)
(,,)
ddd
000
Так как интег-
рал не зависит от пути интегрирования, то берем путь, изображен-
ный на рис. 28.3:
uxxy xyzc xy xyzc
x
y
z
=+++ += ++ +
∫∫∫
0
000
dd d() ().
Задачи для самостоятельного решения
7) Найти векторные линии поля
vM xyjxxj() ().=- -21
Найти поток векторного поля
v
через поверхность G:
8)
v
= {0; 0; -z}, G: z = y, в цилиндре x = 0, y = 0, x + y = 2
(, )
nOZ
— тупой;
9)
vxzi zxjxyk=- +- ++()()(),2345
G — верхняя сторона
АВС с вершинами A(1; 0; 0), B(0; 1; 0), C(0; 0; 1);
10)
v
= {x, y, z}, G: x
2
+ y
2
= R
2
, z = x, z = 0 (z ≥ 0) —
замкнутая поверхность;
11)
vxiyjzk=+ ++() ,12
G: x
2
+ y
2
= z
2
, z = 4 (z ≥ 0) — замк-
нутая поверхность;
12)
v
= {0; 0; z
2
}, G: x
2
+ y
2
+ z
2
= 1.
Вычислить дивергенцию и ротор векторного поля:
13)
vxyz iyxz jzxy k=- +- +-()()();85 85 85
14)
vyzi zxjxyk=+ ++ ++()()();
22 22 22
15)
v
= grad(x
2
+ y
2
+ z
2
).
16) Дано векторное поле
v
= (y - x
2
)
i
+ (z - y)
j
+
+
x
z
k+
1
.
Найти graddiv
v
(M
0
), где M
0
(1; 1; 1).
17) Дано скалярное поле u = x
2
yz
3
. Найти divgradu(M
0
), где
M
0
(-1; 1; 1).
Проверить, являются ли следующие векторные поля потенци-
альными или соленоидальными:
18)
v
= (x + y
2
)
i
- (x
2
+ y
3
)
j
+ z(3y
2
+ 1)
k
;
19)
v
= e
x
siny
i
+ e
x
cosy
j
+
k
.
Найти циркуляцию векторного поля вдоль контура L:
20)
v
= z
i
+ x
j
+ y
k
, L:
xy
z
22
4
0
+=
=
,
;
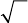
270
21)
v
= {x + y, x - z, y + z}, L — контур ABC, A(1; 0; 0),
B(0; 1; 0), C(0; 0; -1);
22)
v
= y
i
- x
j
+ (x + y)
k
, L:
zx y
z
=+
=
22
1
,
.
Доказать, что векторное поле является потенциальным, и най-
ти его потенциал:
23)
v
= (yz + 1)
i
+ xz
j
+ xy
k
;
24)
v
= (2xy + z)
i
+ (x
2
- 2y)
j
+ x
k
.
варианты контрольной работы
Вариант № 1
1. Вычислить криволинейный интеграл
()(),xyxx yy
L
++-
∫
dd3
где L — ломаная АВС: А(1; 2), В(2; 4), С(3; 0). Ответ: 8.
2. Вычислить криволинейный интеграл
() ,xyxxy
L
-+
∫
2d d
где
L — четверть эллипса х = 2cost, у = 4sint, 0 ≤ t ≤ π/2. Ответ:
6π - 2.
3. Найти первообразную функцию u(x, y) по ее полному диф-
ференциалу du = (x
2
- 2xy
2
+ 3)dx + (y
2
- 2x
2
y + 3)dy. Ответ:
u = x
3
/3 + y
3
/3 - x
2
y
2
+ 3x + 3y + c.
4. Используя формулу Грина, вычислить
(sin )2
2
xy xx
xy
L
ed++
∫
+-+(),xyxy
xy222
2
ed
где L — контур треугольника с вершинами в
точках А(0; 0), В(1; 1), С(1; 0), указанными в порядке обхода.
Ответ: -2/3.
5. Дано скалярное поле
ux
xyz
= e
23
.
Найти величину наибольшей
скорости изменения поля в точке M(0; 1; 1). Ответ: 1.
6. Найти поток векторного поля
vxiyjzk=++
через замкну-
тую поверхность x
2
+ y
2
= 4 - z, z = 0 (z ≥ 0). Ответ: 8π.
Вариант № 2
1. Вычислить криволинейный интеграл
()xy
L
-
∫
3
dх + (у -
- 2х)dу, где L — ломаная АВС: А(1; 0), В(2; 1), С(3; 3). Ответ:
-12.
