Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Нуриева С.Н., Дегтярева О.М. Математика в примерах и задачах
Подождите немного. Документ загружается.

241
2. Вычислить двойной интеграл
(),xyxy
D
+
∫∫
5dd
где ∂D: x = y
2
,
x + 7y + 12 = 0. Ответ: -0,85.
3. Найти объем тела Ω, если: а) ∂Ω: z = 4 - x
2
- y
2
, z = 0,
x
2
+ y
2
= 1; б) ∂Ω: x = z
2
, x = 4 - z
2
, y = 0, y = 6. Ответ:
а) 9π/2; б)
32 2.
4. Изменить порядок интегрирования
ddyfxy x
y
y
-
-
∫∫
2
1
2
2
(, ).
Ответ:
ddddxfxy yxfxyy
x
x
x
x
0
1
1
42
∫∫ ∫∫
--
-
+(, )(,) .
расчетное задание
Здесь n — номер студента по списку группы, αβγδ — четыре
цифры номера группы,
λ
α
=
+
+
n
4
1;
µ
β
=
+
+
n
5
1;
ν
γδ
=
++
+
n
5
1;
l
n
=
+
3
4
;
k
n
=
+
3
2
.
]...[ — остаток от деления, [...] — целая часть от деления.
1. Вычислить двойной интеграл
(( ())(() )) ,λλµµ+- ++-
+
∫∫
11
1nn
D
xyxydd
D — треугольник АВО: О(0; 0),
A
n
v
n
2
2
2
2
ν
ππ
sin;cos,
B
nn nn
ν
ππ
ν
ππ
sincos ;cos
()
sin
()
.
22
1
2
1
2
+
+
+
+
2. Вычислить двойной интеграл
(),xy xy
D
22
+
∫∫
λ
dd
D:
xy
x
n
y
n
yx
ln
22 2
22
11
+≤
≤
-≤-
µ
ππ
,
sincos ,
() ().
242
3. Найти объем V
Ω
:
∂
=- -
+-
+
+-
+
Ω:
zl x
n
y
n
x
nn
2
1
22
11
2
11
2
µ
π
λ
π
cossin ,
() ()
yyx
n
y
n
z
=+
=
λ
π
µ
π
22
22
0
sincos ,
.
4. Найти координаты центра тяжести однородной пластинки D,
если
∂
=
-
+-+++
=
-
D
y
x
l
n
xlxl
n
y
x
l
:
sinsin (( ))cos,
()
sin
λπ
λλλ
π
λ
π
π
2
2
2
2
22
nnlxn
x
k
22 2
10
-
-
->
()
cos,
() .
λπ
5. Вычислить
11
2
11
2
2
1
2
+-
+
+-
+
∫∫∫
() ()
,
nn
xz yz xyzddd
Ω
∂
==+
++-=
==
Ω:
zz
xy
n
xy
n
xy
λµ
ππ
ν
,,
()sin()cos ,
,.
3
22
00
6. Найти массу тела Ω: x
2
+ y
2
≤ z ≤ 2ν
2
- x
2
- y
2
, если его
плотность r = (µ + (-1)
n
µ)x
2
+ (λ + (-1)
n+1
λ)y
2
.
Ответы к разд. 23, 24
23. Двойной интеграл
1)
15
2
3
32
+-();ee
2) а) -4/3; б) -14/27; 3) а) 1/2; б) -2;
4) а)
51
20
;
б)
64 2
3
;
5) 9/4; 6) 12; 7) 0; 8)
π
6
;
9) 0; 10)
π
2
2ln ;
11) 0;
12) 3π; 13)
π
4
1
2
- ;
14)
ddyfxy x
y
y
0
1
3
∫∫
(, );
15)
ddddyfxy xyfxyx
y
y
y0
3
83
24
8
3
∫∫ ∫∫
+(, )(,) ;
ddddyfxy xyfxyx
y
y
y0
3
83
24
8
3
∫∫ ∫∫
+(, )(,) ;
16)
ddyfxy x
y
y
0
4
4
4
∫∫
--
-
(, );
17)
ddxfxy y
x
x
-
-
-
∫∫
1
0
2
2
2
(, );
18)
ddxfxy y
x
x
-
-
∫∫
1
02
2
2
(, );
19)
ddyfxy x
y
y
-
--
∫∫
1
0
2
2
(, );
20)
16 15
3
;
21) 7,5 -
- 8ln2; 22)
42
2
3
;
23)
12
4
21
;
24)
44
15
2
13
3
+ ;
25)
20
3
;
26)
2
3
3
am
;
27) 8ln2; 28)
43
3
π a ;
29)
45
64
15
8
π+ ;
30) 13; 31)
();73 14626-
32)
42π;
33)
25513π();-
34)
16
15
64
21
;;
35)
4
3
1
π
;;-
36)
5
14
38
35
;;
37)
-+
-
-
-
242
82 2
2
82 2
ππ
()
;
()
.
24. Тройные и n-кратные интегралы
1) 2; 2) 1/6; 3)
81
4
;
4)
-+
32 16
32
ππ
;
5) 8; 6) 0; 7) 2π; 8)
π
2
;
9)
272
15
π
;
10)
64
3
π
;
11)
3
20
;
12) 4/3; 13)
4
3
π
;
14) (0; 0; 4); 15)
1
12
1
24
1
36
;; ;
16)
0
3
23 1
0;
()
;;
π-
17)
2
0
3
22
π
;; ;
18)
-
1
2
0
5
4
;; .
244
Глава 9
векторный анализ
25. криволинейный интеГрал
По длине дуГи (I рода)
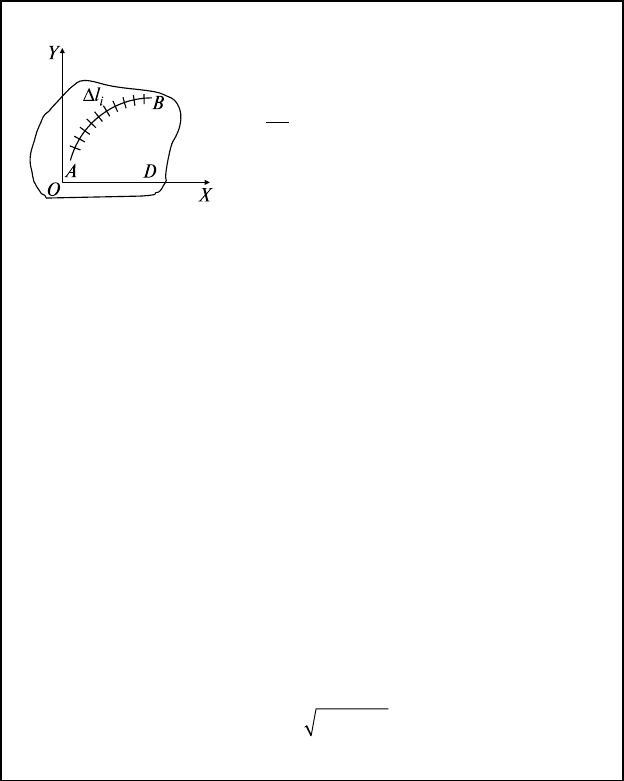
опорный конспект № 25
25.1. Понятие Ки Iр
О: f(x, y) непр. в D,
AB D
∪
⊂ ,
AB
∪
разбивается на
AA
ii-
∪
1
длиной
∆l
i
,
in= 1,,
M
i
(ξ
i
, η
i
) ∈ ∆l
i
⇒
fxyl fl
AB
l
ii i
i
n
i
(, )lim (, )
max
d
∪
∫
∑
=
→
=
∆
∆
0
1
ξη
r(x, y) — линейная плотность
AB
∪
⇒
mfxy l
AB
=
∪
∫
(, )d
— масса AB
25.2.Свойства Ки Iр
1
0
.
((,) (, )) .fxyfxy lflfl
AB AB AB
12 12
+=+
∪∪∪
∫∫∫
ddd
2
0
.
cf xy lcfxyl
AB AB
(, )(,),dd
∪∪
∫∫
=
c = const.
3
0
.
LL Lfxy lflfl
LLL
=+⇒=+
∫∫∫
12
12
(, ).ddd
4
0
.
dll
L
∫
=
— длина L.
5
0
.
fxyl fxyl
AB BA
(, )(,)dd
∪∪
∫∫
=
25.3. Вычисление Ки Iр
а)
AB
∪
:
х = х(t), y = y(t) — непр. дифф. на [α, β] ⇒
⇒=
′
+
′
∪
∫∫
fxyl fxtytx yt
AB
(, )((),()) ;dd
α
β
22
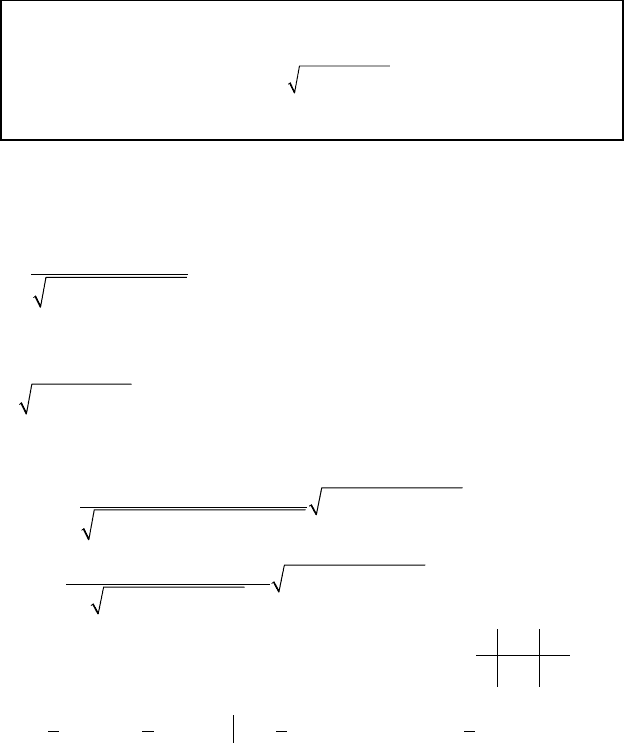
245
б)
AB
∪
: у = у(х) — непр. дифф. на [а, b] ⇒
⇒= +
′
∪
∫∫
fxyl fxyx yx x
AB
a
b
(, )(,()) (())dd1
2
Задачи к разд. 25
Задача 1. Вычислить криволинейный интеграл J =
J
xyl
xxy
y
L
=
-
++
∫
()
,
2
2
3
27 982
ed
где L — дуга кубической параболы у = х
3
- 9х,
заключенная между точками А и В с абсциссами, равными -3 и -2
соответственно.
Решение: Элемент дуги dl вычисляется по формуле dl =
ddlyxx=+
′
1
2
(()) .
Так как у′ = 3х
2
- 9, то 1 + (у′(х))
2
= 1 + (3х
2
-
- 9)
2
= 9х
4
- 54х
2
+ 82. Подставляя выражение для у и dl, полу-
чим (см. ОК, разд. 25.3)
J
xxx
xxxx
xx x
x
xx
L
=
--
+-+
-+ =
=
-
∫
()()
()
(
23 9
23
42
2
39
27 9982
95482
3
e
d
---
-+
-+ =
=--
-
-
-
∫
39
95482
95482
3
39
42
3
2
42
23
3
)( )
()(
xx
xx
xx x
xx
xx
e
d
99
9
39
32
010
3
9
3
2
3
2
xx
xxt
xxt
x
t
xx
)
,
(),
ed
dd
-
-
-
∫
=
-=
-=
--
==
==-= -+=+
∫
1
3
1
3
1
3
10
1
3
91
0
10
0
10
10 10 010
tt teee e
ttt
ed ee()()().
Задача 2. Вычислить
(),xyl
L
+
∫
d
где L — контур треугольника
АВО с вершинами А(1; 0), В(0; 1), О(0; 0).
Решение: Уравнение прямой, проходящей через точки А и В,
имеет вид у = 1 - х, 0 ≤ х ≤ 1, уравнение прямой ОВ — х = 0,
0 ≤ у ≤ 1, уравнение прямой ОА — у = 0, 0 ≤ х ≤ 1.
Тогда
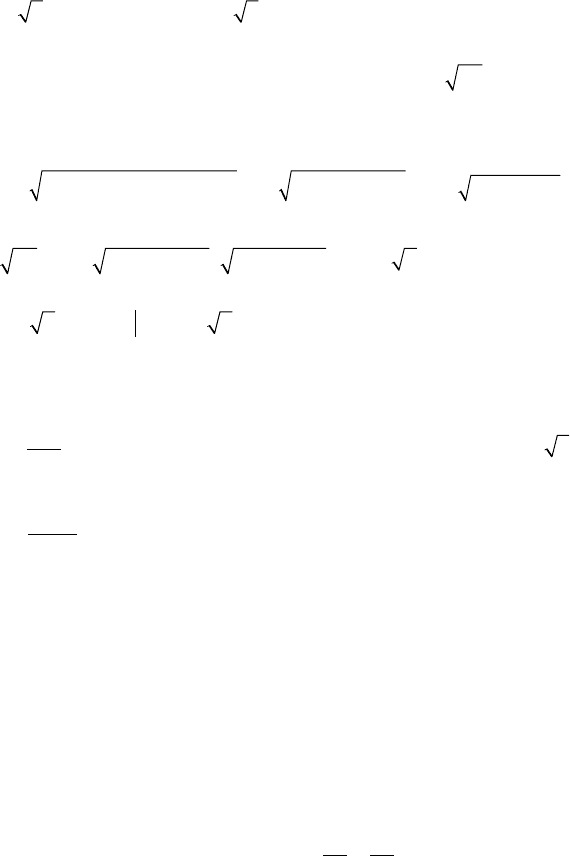
246
() () () ()xylxyl xylxyl
xyy
L
AB BO OA
+= +++++=
=+
∫∫∫∫
∫
∪∪∪
dddd
dd2
0
1
0
11
0
1
21
∫∫
+=+xxd .
Задача 3. Вычислить криволинейный интеграл
2yl
L
d
∫
,
где L —
дуга циклоиды х = а(t - sint), y = a(1 - cost), 0 ≤ t ≤ π.
Решение: Находим
ddddla ta tt atta tt=-+=-=-
2222 2
12221(cos )sin (cos )(cos) .
В исходный интеграл подставляем выражение для у и dl:
2212121
2
00
yl atattaatt
aat
L
ddd
∫∫ ∫
=- -= -=
=-
(cos )(cos) (cos )
(s
ππ
iin ).taa
0
2
π
π=
Задачи для самостоятельного решения
Вычислить криволинейные интегралы:
1)
xl
y
L
d
∫
,
где L — дуга параболы y
2
= 2x между точками А(1;
2
),
В(2; 2);
2)
dl
xy
L
+
∫
,
где L — отрезок прямой y = x + 2, соединяющий
точки А(2; 4), В(1; 3);
3)
xy l
L
d
∫
,
где L — контур прямоугольника, ограниченного пря-
мыми x = 0, y = 0, x = 4, y = 2;
4)
xl
L
d
∫
,
где L —
отрезок прямой, соединяющий точки А(0; 0) и
В(1; 2);
5)
yl
L
3
d
∫
,
где L — первая арка циклоиды х = а(t - sint), y =
= a(1 - cost);
6)
xy l
L
d
∫
,
где L — четверть эллипса
x
a
y
b
2
2
2
2
1+=,
лежащая в пер-
вом квадранте;
247
7) С помощью криволинейного интеграла найти длину астро-
иды x = acos
3
t, y = asin
3
t.
8) Найти массу m дуги окружности x = cost, y = sint
(0 ≤ t ≤ π), если линейная плотность ее в точке (х, у) равна у.
26. криволинейный интеГрал
По координатам (ки II рода)
опорный конспект № 26
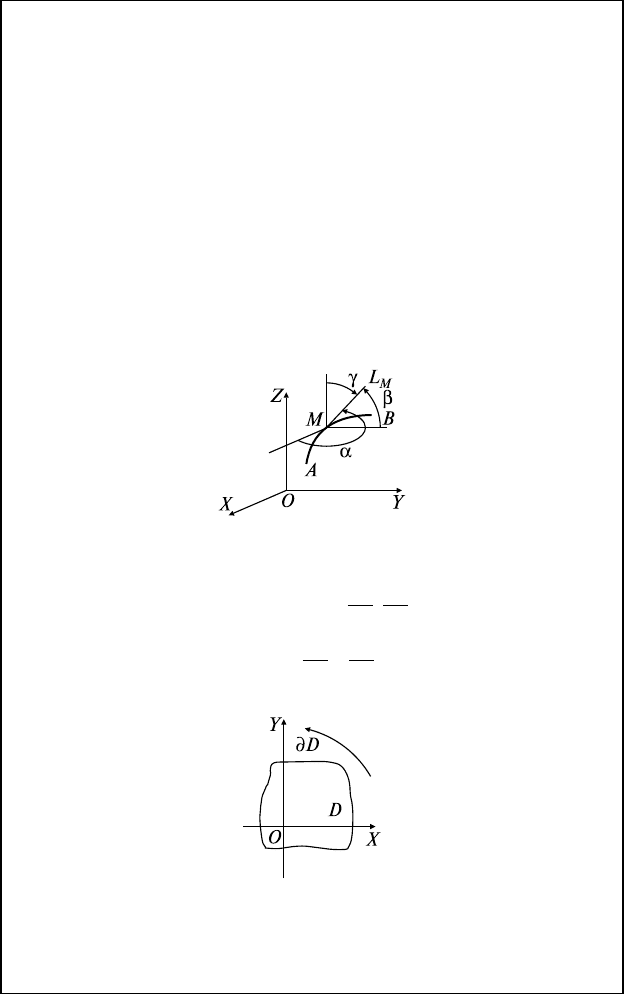
26.1. Определение Ки IIр. Задача о работе
a
= {P(x, y), Q(x, y)}
P(x, y), Q(x, y) — непр. в D,
AB D
∪
⊂
AB
∪
разбивается на
AAin
ii-
∪
=
1
1,,,
AA xyMAA
ii ii ii ii--
∪
=∈
11
{, }, (, ),∆∆ ξη
ar Px Qy PxQ
AB AB
xy
ii i
i
i
ii
⋅= += +
∪∪
∫∫
∑
→
ddd lim(,) (
max,
()
∆∆
∆
0
ξη ξ ,,)η
ii
y∆
WPxQyFr
AB AB
=+=⋅
∪∪
∫∫
dd d
— работа силы
F
= {P(х, y),
Q(x, y)} на
AB
∪
,
d
r
= {dx, dy}
26.2. Свойства Ки IIр
1
0
.
Px Qy Px Qy
AB BA
dd dd
∪∪
∫∫
+=-+.
2
0
.
AB AC CB Px Qy Px Qy Px Qy
AB AC CB
∪∪∪
=+⇒+=+++
∪∪∪
∫∫∫
dd dd dd.
3
0
. D = D
1
+ D
2
, ∂D
1
= L
1
, ∂D
2
= L
2
, ∂D = L ⇒
⇒+=+
∫∫∫
Px Qy
LLL
dd
21
26.3. Вычисление Ки IIр
1)
AB
∪
: x = x(t), y = y(t) — непр. дифф. на [α, β] ⇒
⇒+=
′
+
′
∪
∫∫
Px Qy PxtytxtQxt yt yt t
AB
dd d(((),()) () ((), ())())
α
β
248
2)
AB
∪
: y = y(x) — непр. дифф. на [a, b] ⇒
⇒+=+
′
∪
∫∫
Px Qy Pxyx Qx yx yx x
AB
a
b
dd d((,()) (, ())())
26.4. Связь между Ки Iр и IIр
L
M
— касательная к
AB
∪
в т. М,
αβγ===⇒(, ), (, ), (, )LOXLOY LOZ
MMM
⇒++=
∪
∫
Pxyz xQxyzy Rx yz z
AB
(, ,) (, ,) (, ,)ddd
=++
∪
∫
(cos coscos )PQRl
AB
αβγ d
26.5. Формула Грина
P(x, y), Q(x, y) непр. в D вместе с
∂
∂
∂
∂
P
y
Q
x
,,
LD Px Qy
Q
x
P
y
xy
LD
=∂ ⇒+=
∂
∂
-
∂
∂
∫∫∫
dd dd
249
26.6. Условия независимости Ки IIр от контура интегрирования
1.
Px Qy LD
L
dd *
*
∫
+=∀⊂⇔0
2.
Px Qy
AB
dd
∪
∫
+
не зависит от
AB D
∪
⊂⇔
3. Pdx + Qdy = du, u = u(x, y), (x, y) ∈ D ⇔
4.
∂
∂
=
∂
∂
P
y
Q
x
в D
26.7. интегрирование полных дифференциалов
Px Qy uuxy Px Qy c
cPxy
xy
xy
CBAC
ddddd+=⇒= ++=
=++=
∫
∫∫
(, )
(,
(,)
(,)
00
0
))(,)ddxQxy yc
x
x
y
y
00
∫∫
++
26.8. Уравнения в полных дифференциалах
P(x, y)dx + Q(x, y)dy = 0,
∂
∂
=
∂
∂
⇒+=
∫∫
P
y
Q
x
Pxyx Qx yy c
x
x
y
y
(, )(,)
0
00
dd
— общий интеграл
Задачи к разд. 26.1–26.3
Задача 1. Вычислить интеграл
xy xxyy
L
dd
∫
++(),
принимая за
линию L:
а) отрезок прямой, соединяющий точки О(0; 0) и А(1; 1);
б) дугу параболы у = х
2
, соединяющую эти же точки;
в) ломаную ONA: O(0; 0), N(1; 0), A(1; 1) (рис. 26.1).
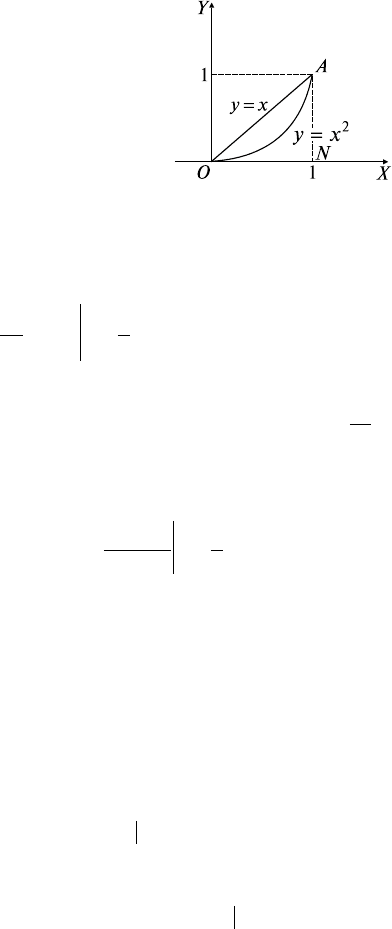
250
Решение: а) кривой интегрирования L служит прямая у = х,
следовательно, dx = dу и (см. ОК, разд. 26.3)
Ixxx
x
x=+ =+
=
∫
() ;
2
0
1
3
2
0
1
2
3
4
3
d
Ixxx
x
x=+ =+
=
∫
() ;
2
0
1
3
2
0
1
2
3
4
3
d
б) интегрирование ведется по параболе у = х
2
. Поэтому
dу = 2хdx и
Ixxx xx=++⋅ =
∫
(( )) ;
32
0
1
2
17
12
d
в) контур интегрирования L разбиваем на две части. На участке
ON y = 0, dy = 0; на участке NA x = 1, dx = 0. Поэтому I =
Iyy
y
=+ =
+
=
∫
()
()
.1
1
2
3
2
0
1
2
0
1
d
Задача 2. Вычислить интеграл
yx xy
L
dd-
∫
,
где L — первая арка
циклоиды х = 2(t - sint), у = 2(1 - cost), 0 ≤ t ≤ 2π.
Решение: Так как dx = 2(1 - cost)dt, dy = 2sintdt, то (см. OK,
разд. 26.3)
Ittttt tt tt=- -- =--=
∫∫
[( cos) (sin )sin ](cossin )41 4422
2
0
2
0
2
dd
ππ
==- -
∫
42 2
0
2
0
2
[( sin) sin].tt ttt
π
π
d
Интегрируя последний интеграл по частям, получим
Ittt=--+ =16 424
0
2
ππ
π
(cos sin) .
Рис. 26.1
