Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Нуриева С.Н., Дегтярева О.М. Математика в примерах и задачах
Подождите немного. Документ загружается.

141
Задача 2. Записать комплексное число
z
i
i
i=
+
-
++
23
45
7
41
19
41
в
алгебраической форме.
Решение: Применим правила умножения, деления и сложения
комплексных чисел в алгебраической форме (ОК, разд. 13.2):
z
i
i
i
ii
ii
i=
+
-
++ =
++
-+
++ =
=
23
45
7
41
19
41
2345
4545
7
41
19
41
()()
()()
(
22345
16 25
7
41
19
41
8101215
16 25
7
41
19
41
2
2
++
-
++ =
+++
+
++
ii
i
i
iii)( )
ii
i
iiiii
=
=
-+ +
++ =- +++==
8151012
41
7
41
19
41
7
41
22
41
7
41
19
41
41
41
()
..
Задача 3. Выполнить действия, используя показательную форму
комплексного числа:
wi
i
=-+().333
4
2
5
e
π
Решение: Запишем число z = -3 + 3
3
i в показательной форме
z = re
iϕ
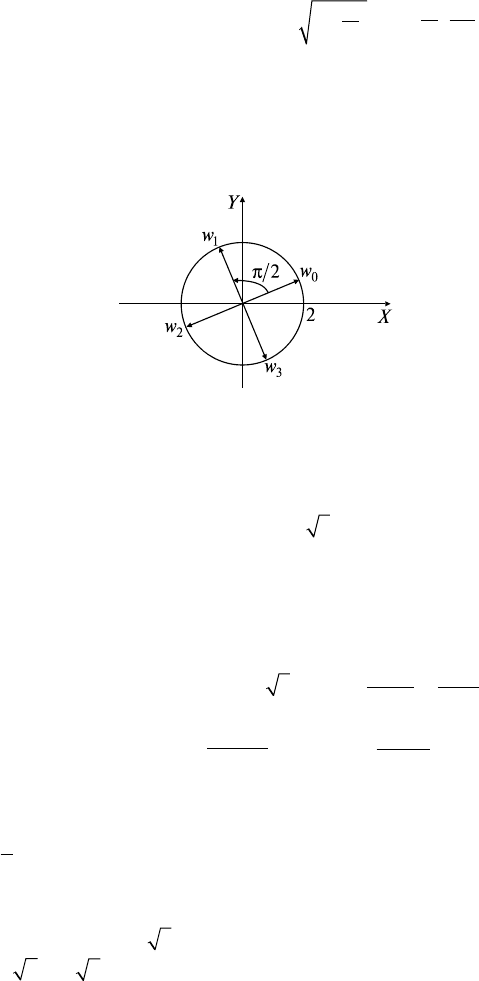
, используя формулы ОК, разд. 13.3. Модуль числа z, изо-
браженного на комплексной плоскости вектором
OM
, равен r =
= |
OM
| =
927+
= 6.
Для аргумента z имеем tgϕ = 3
3
/(-3) = -
3
. Поскольку
OM
находится во второй четверти, то ϕ = 2π/3 (рис. 13.2). Таким обра-
зом, z = 6e
2πi/3
.
Находим w = z
4
e
2πi/5
= 6
4
e
8πi/3
e
2πi/5
= 1296e
(8π/3+2π/5)i
=
= 1296e
46πi/15
= 1296e
(2π+16π/15)i
= 1296e
16πi/15
.
Рис. 13.2
Задача 4. Найти все значения
wi=-16
4
.
Решение: Найдем показательную форму комплексного числа
z = -16i. Определяем
r =+-=01616
2
() ,
tgϕ ∃/ в силу расположе-
ния чисто мнимого числа -16i, аргумент ϕ = 3π/2.
142
Таким образом, z = 16e
3πi/2
,
w
i
k
i
==
+
16 2
3
2
4
3
8
2
4
ee
π
ππ
.
Имеем
четыре различных значения w при k = 0, 1, 2, 3: w
0
= 2e
3πi/8
,
w
1
= 2e
i(3π/8+π/2)
= 2e
7πi/8
, w
2
= 2e
i(3π/8+π)
= 2e
11πi/8
, w
3
=
= 2e
i(3π/8+3π/2)
= 2e
15πi/8
. Полученные значения располагаются на
комплексной плоскости на окружности с центром в начале коор-
динат и радиусом 2 (рис. 13.3).
Рис. 13.3
Задачи для самостоятельного решения
1) Построить на комплексной плоскости комплексные числа:
z = -3 + 5i, z = 4 - i, z = 3i, z =
3
+ i и им сопряженные.
2) Найти комплексные корни следующих квадратных уравне-
ний и изобразить их на комплексной плоскости:
а) 4z
2
- 2z + 1 = 0; б) 2z
2
+ 4z + 3 = 0.
3) Записать в алгебраической форме следующие комплексные
числа:
а) (1 - i)
2
(5 + 8i); б) (1 + i
3
)
3
; в)
1
13
1
4+
+
-ii
;
г) i
12
+ i
17
; д)
23
1
2
+
+
i
i()
;
е)
i
i
5
19
2
2
1
+
+
.
4) Записать в алгебраической форме следующие комплексные
числа:
а)
1
2
e
iπ
;
б) е
4+πi/2
; в) 6е
πi/3
; г) 3е
-πi/4
; д) е
1+2πi/3
.
5) Представить в тригонометрической и показательной формах
следующие комплексные числа:
а) -1 + i; б)
3
+ i; в) -5i; г) 7;
д) -
2
+ i
6
; е) -tgα + i; ж) cos(π/7) + isin(π/7).
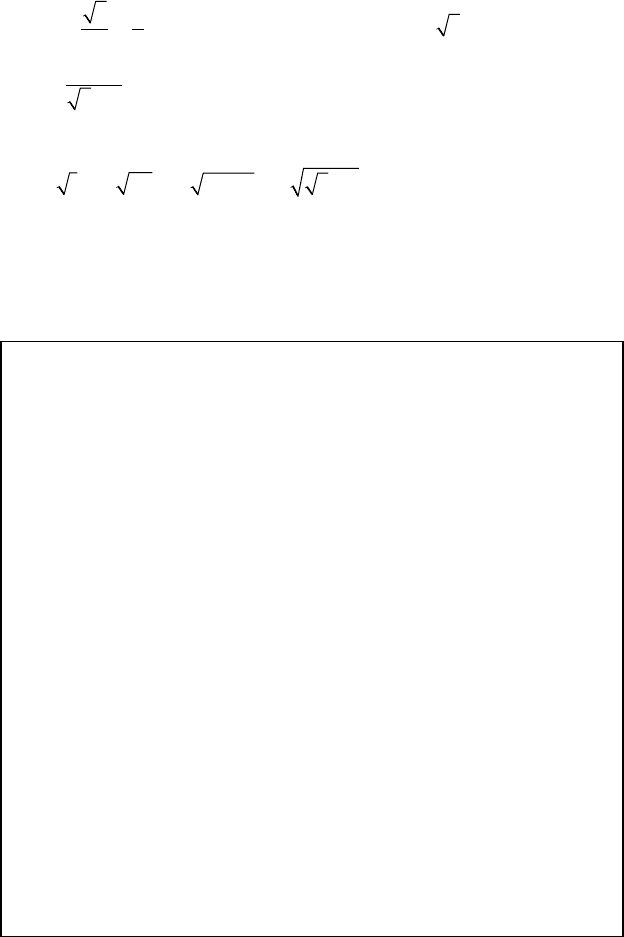
143
6) Используя показательную форму комплексного числа, вы-
полнить указанные действия:
а)
-+
3
2
3
2
6
i ;
б) (2 + 2i)
5
; в) (1 - i)
3
(-2
3
+ 2i);
г)
1
3
4
-
+
i
i
.
7) Найти все значения следующих корней и изобразить их на
комплексной плоскости:
а)
i
3
;
б)
-8
6
;
в)
-+1
5
i;
г)
3
4
+ i.
14. Функции комПлексноГо ПеременноГо (ФкП)
опорный конспект № 14
14.1.Области и линии на комплексной плоскости Z.
Понятие ФКП
Комплексная плоскость вместе с z = ∞ — расширенная ком-
плексная плоскость Z
О: Окрестность U
δ
(z
0
) ⇔ z: |z - z
0
| < δ
О: w = f(z), z ∈ D ⊂ Z, w ∈ G ⊂ W ⇔ D →:
→: G: ∀ z ∈ D ∃ w ∈ G
W = f(z) — однозначная или многозначная ФКП
W = f(z): D ↔ G ⇔ f(z) — однолистна
z = x + iy, w = u + iv ⇒ w = f(z) = u(x, y) + iv(x, y),
u(x, y) = Ref(z), v(x, y) = Imf(z)
z = re
iϕ
⇒ w = f(z) = u(r, ϕ) + iv(r, ϕ)
14.2. Предел и непрерывность ФКП
О: a =
lim()
zz
fz
→
0
⇒ ∀e > 0 ∃ δ = δ(e): 0 < |z - z
0
| < δ ⇒
⇒ | f(z) - a| < e
Т:
lim()lim (,),
(,)(,)zz xy xy
fz auxy a
→→
=⇔ =
000
1
lim(,) ,.
(,)(,)xy xy
vx yaaa ia
→
==+
00
212
О: w = f(z) непрерывна в т. z
0
⇔
1) f(z) определена в U
δ
(z
0
);
2)
lim()().
zz
fz fz
→
=
0
0
Непрерывность f(z) в т. z
0
⇔
непрерывности u(x, y), v(x, y) в т. (x
0
, y
0
)

144
14.3. Производная ФКП. Условия Коши—Римана
О: w = f(z) — однозначная ФКП,
′
==
+-
→→
fz
w
z
fz zfz
z
zz
() limlim
()()
∆∆
∆
∆
∆
∆
00
Т: f (z) = u(x, y) + iv(x, y) — дифференцируема
в т. z = x + iy ⇔
∂
∂
=
∂
∂
∂
∂
=-
∂
∂
u
x
v
y
u
y
v
x
,
(условия Коши—Римана)
′
=
∂
∂
+
∂
∂
=
∂
∂
-
∂
∂
=
∂
∂
-
∂
∂
=
∂
∂
+
∂
∂
fz
u
x
i
v
x
v
y
i
u
y
u
x
i
u
y
v
y
i
v
x
()
14.4. Понятие аналитической функции.
Сопряженные гармонические функции
О: Однозначная функция w = f(z) аналитическая
в т. z = z
0
⇔ f(z) дифференцируема в U
δ
(z
0
)
Однозначные функции w = z
n
, n ∈ N, z ≠ 0, w = e
z
,
w = sinz, w = cosz аналитичны в Z
О: u(x, y), (x, y) ∈ D, — гармоническая в D ⇔
∂
∂
∂
∂
2
2
2
2
u
x
u
y
,
— не-
прерывны и
∂
∂
+
∂
∂
=
2
2
2
2
0
u
x
u
y
Т: f(z) = u(x, y) + iv(x, y) — аналитическая в D ⇒ u(x, y),
v(x, y) — гармонические в D
О: u(x, y), v(x, y) — сопряженные гармонические функции при
выполнении условий Коши—Римана
Т: u(x, y) — гармоническая в D ⇒ ∃ сопряженная к ней гар-
моническая функция v(x, y) такая, что f(z) = u(x, y) + iv(x, y) —
аналитическая в D
Задачи к разд. 14
Задача 1. Какие множества точек комплексной плоскости зада-
ются:
а) равенством ||z — z
1
| - |z - z
2
|| = 2a;
б) неравенством 0 < argz < π/4?
Решение: а) модуль разности двух комплексных чисел равен
расстоянию между точками, изображающими эти числа:
|z - z
1
| = |(x - x
1
) + i(y - y
1
)| =
()(),xx yy-+-
1
2
1
2
поэтому,
обозначая точки М(z), M
1
(z
1
), M
2
(z
2
), получаем ||MM
1
| - |MM
2
|| = 2a.

145
Используя определение гиперболы, делаем вывод, что это гипер-
бола с фокусами в точках M
1
, M
2
и действительной полуосью а;
б) используя определение argz как главного значения Argz,
заключаем, что это угол π/4 с вершиной в точке z = 0, расположен-
ный выше оси ОХ, которая является одной из его сторон.
Задача 2. Найти значения функций: а) sin2i; б) ln(1 + i).
Решение: а) по определению тригонометрической функции
sin z
i
iz iz
=
-
-
ee
2
имеем
sin;
() ()
2
222
2222 22
i
ii
i
ii ii
=
-
=
-
=
-
-- -
ee eeee
б) по определению логарифмической функции Lnz = ln|z| +
+ iArgz; Ln(1 + i) = ln|1 + i|| + iArg(1 + i) = ln
2
+ iarg(1 + i) +
+ 2πk = ln
2
+ i(π/4 + 2πk).
Задача 3. Найти действительную и мнимую части функции
w = sinz.
Решение: По определению при z = x + iy имеем
sin
(cos sin) (cos s
z
ii
xi xxi
iz iz ix yixy
yy
=
-
=
-
=
=
+- -
---+
-
ee ee
ee
22
iin )
cos( )sin ()
sin
()
cos
y
i
xix
i
xix
yy yy
yy
2
2
2
=
=
-+ +
=
=
+
-
--
-
ee ee
ee
(()
.
ee
-
-
yy
2
Обозначим
ee
yy
y
+
=
-
2
ch
— гиперболический косинус,
ee
sh
yy
y
-
=
-
2
— гиперболический синус. Тогда Rez = sinxchy,
Imz = cosxshy.
Задача 4. Установить, дифференцируемы ли функции, и найти
производные, если они существуют: а) w = 1/z; б) w = |z|. Явля-
ются ли функции аналитическими?
Решение: Выделим действительную и мнимую части функций и
проверим выполнение условий Коши—Римана:
а)
wz
xiy
xiy
xy
==
+
=
-
+
1
1
22
,
146
(Re)
()()
,w
x
xy
xy x
xy
yx
xy
x
x
′
=
+
′
=
+-
+
=
-
+
22
22 2
222
22
222
2
(Re)
()
,w
x
xy
xy
xy
y
y
′
=
+
′
=
-
+
22 222
2
(Im)
()
,w
y
xy
xy
xy
x
x
′
=
-
+
′
=
+
22 222
2
(Im)
()()
.w
y
xy
xy y
xy
yx
xy
y
y
′
=
-
+
′
=
-- +
+
=
-
+
22
22 2
222
22
222
2
Итак,
∂
∂
=
∂
∂
Re Im
,
w
x
w
y
∂
∂
=-
∂
∂
Re Im
.
w
y
w
x
Функция w = 1/z ана-
литическая при z ≠ 0 и w′(1/z)′ = -1/z
2
;
б)
wz xy== +
22
— действительная функция,
∂
∂
=
∂
∂
=
+
Re
,
w
x
w
x
x
xy
22
∂
∂
=
∂
∂
=
+
Re
,
w
x
w
x
x
xy
22
∂
∂
=
Im
.
w
y
0
Функция не является аналитической.
Задача 5. Определить аналитическую функцию по известной
действительной части u = x
2
- y
2
+ 2x.
Решение: Если z
0
— точка аналитичности w = f (z), то
fz u
zzzz
i
ux yic() ,(,) ,=
+-
-+2
22
00
00
c — const. Полагая z
0
= 0,
имеем
w
zz
i
zicz zic=
-
++=++2
22
22
22
2
.
Задачи для самостоятельного решения
1) Выяснить, какие множества точек комплексной плоскости
задаются:
равенствами: а) |z - z
1
| + |z - z
2
| = 2a; б) Imz = 3; в) Re(1/z) =
= 1/2; г) |z| = 1 - Rez;
неравенствами: д) 1 < |z - 2| < 3; е) 1 < Rez < 2.
2) Найти значения функций: а) сos(1 + 3i); б) Ln(
3
+ i);
в) tg5i.
3) Используя уравнения z = sinw, z = tgw, вывести формулы:
Arcsin (),ziiz z=- +-Ln 1
2
Arctg.z
iiz
iz
=-
-
+2
Ln
4) Найти действительную и мнимую части функций:
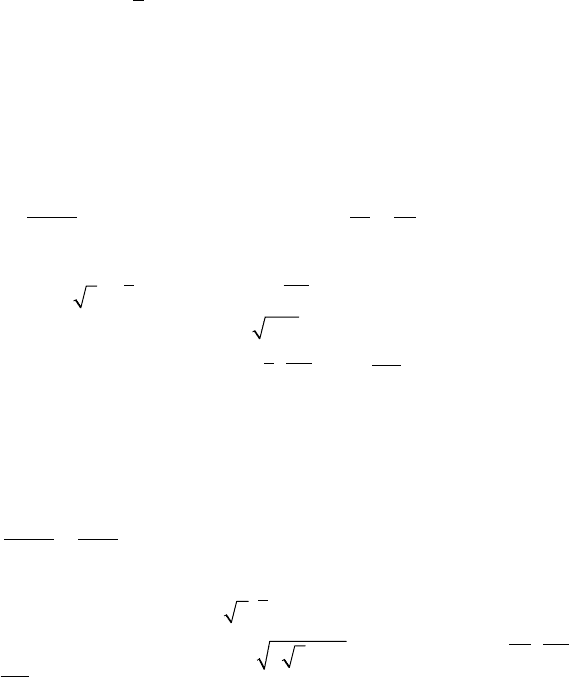
147
а) w = z
3
- 2z
2
; б)
w
z
= e
2
;
в) w = tgz.
5) Установить, являются ли аналитическими функции, и найти
в случае положительного ответа производные: а) w = z
2
- 2iz;
б)
w
iz
= e
2
;
в)
wz= .
6) Определить аналитическую функцию по известной действи-
тельной части: а) 3x
2
y - y
3
+ 5x; б) x
3
+ 6x
2
y - 3xy
2
- 2y
3
.
варианты контрольной работы
Вариант № 1
1. Записать комплексное число в алгебраической форме:
z
i
i
ii=
-
++ +
17
32
212()().
Ответ:
zi=- +
2
13
68
13
.
2. Записать комплексное число в показательной форме:
wi
i
=-
-
().13
5
e
π
Ответ:
w
i
= 2
22
15
e
π
.
3. Найти все значения
w =-32
5
и изобразить их на комплекс-
ной плоскости. Ответ:
wk
k
k
i
==
+
204
5
2
5
e
ππ
,,.
4. Найти значение функции w = z
3
+ 2z при z = 1 + i.
Ответ: 4i.
Вариант № 2
1. Записать комплексное число в алгебраической форме:
z =
23
213
7
-
-
-
-
i
i
i
i
.
Ответ: -1,7 + 0,1i.
2. Записать комплексное число в показательной форме:
w = (1 + i)
9
. Ответ:
w
i
= 16 2
4
e
π
.
3. Найти все значения
wi=-43 4
3
.
Ответ:
w
k
k
i
=
+
8
11
18
2
3
e
ππ
,
k = 02,.
4. Найти значение функции w = z
2
+ 2/z при z = 1 - i.
Ответ: 1 - i.
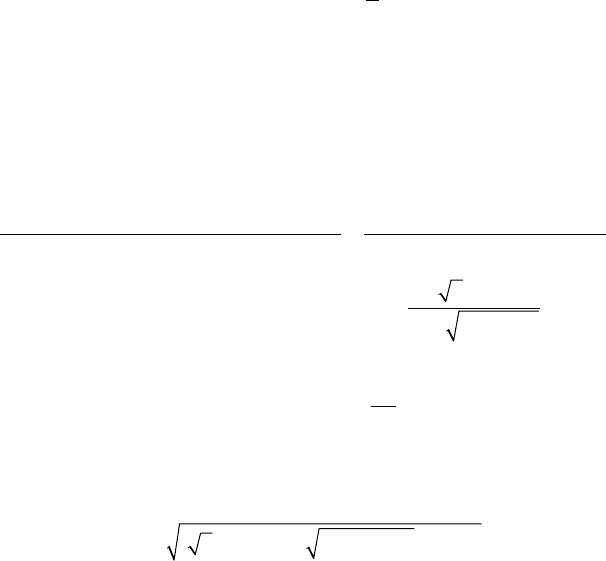
расчетное задание
теоретические вопросы
1. Алгебраическая форма комплексного числа, его изображения
на комплексной плоскости, действия над комплексными числами
в алгебраической форме.
148
2. Тригонометрическая и показательная формы комплексного
числа.
3. Умножение, деление и возведение в целую положительную
степень комплексных чисел, заданных в тригонометрической или
показательной форме.
4. Извлечение корня целой положительной степени из комп-
лексного числа.
задания
Введены следующие обозначения: n — номер студента в списке,
λ = [n/4] — целая часть дроби, µ =
n
4
— остаток при делении
числа на 4, ν — последняя цифра в номере группы.
Задание 1. Найти комплексные корни квадратного уравнения и
изобразить их на комплексной плоскости: (ν + 1)
2
z
2
- 2z(λ +
+ µ)(ν + 1) + 2λ
2
+ µ
2
+ 1 + 2λ(µ + 1) = 0.
Задание 2. Выполнить действия над комплексными числами в
алгебраической форме:
5947312
84
11
1
22 22
λµ λµ λµ
λµ
λννλ
λ
--++---
-- -
+
--++++
+
i
i
i()
()
(())
+++i()
.
ν 1
Задание 3. Дано комплексное число
z
i
i
=
++-
+
()
()
2
121
λµν
λ
:
а) записать его в алгебраической, тригонометрической и пока-
зательной формах;
б) вычислить произведение
wz
i
=
+
3
1
e
π
µ
,
используя показатель-
ную форму числа z, ответ записать в тригонометрической форме
со значением аргумента 0 ≤ argw < 2π.
Задание 4. Найти все значения корня и изобразить на комплекс-
ной плоскости:
()(()).221
11 1
3
λµνλµν
µ
+++++
+
+- +ii
Задание 5. Определить величину тока I в цепи (рис. 14.1), к ко-
торой подведено напряжение 220 В частотой 50 Гц, если активное
сопротивление R = λ + µ (Ом), а индуктивность L = 0,012 +
+ (10(µ + 1) + ν) ⋅ 10
-3
(Гн).
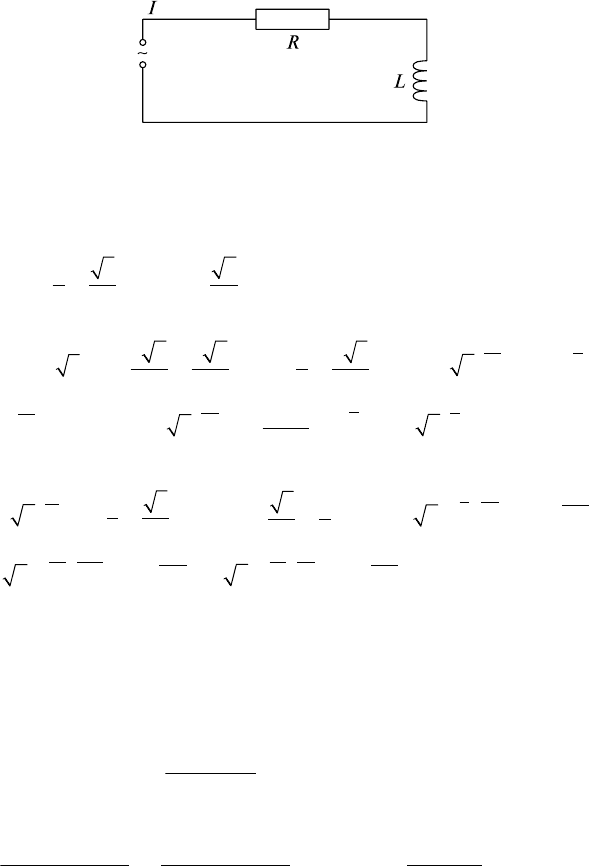
Ответы к разд. 13, 14
13. Комплексные числа
2) а)
1
4
3
4
± i;
б)
-±1
2
2
i;
3) а) 16 - 10i; б) -8; в) 57/170 -
- 41i/170; г) 1 + i; д) 1,5 - i; е) -2 + 1,5i; 4) а) -0,5; б) i e
4
;
в) 3 + 3
3
i; г)
32
2
32
2
- i;
д)
-+
ee
2
3
2
i;
5) а)
2
3
4
e
π
i
;
б)
2
6
e
π
i
;
в)
5
3
2
e
π
i
;
г) 7е
i⋅0
; д)
22
2
3
e
π
i
;
е)
1
2
cos
;
α
α
π
e
±
i
ж)
2
7
e
π
i
;
тригономет-
рическая форма: re
iα
= r(cosα + isinα); 6) a) 27; б) -128 - 128i;
в)
82
12
e
πi
;
г)
1
8
3
8
+ i;
7) а)
±+-
3
22
i
i,;
б)
2
63
e
i
kππ
+
,
k = 05,;
в)
2
10
3
20
2
5
e
i
kππ
+
,
k = 04,;
г)
2
4
24 2
e
i
kππ
+
,
k = 03,.
14. Функции комплексного переменного
1) а) эллипс с фокусами z
1
, z
2
; б) прямая y = 3; в) окружность
(x - 1)
2
+ y
2
= 1; г) парабола y
2
= 1 - 2x; д) кольцо между
окружностями с центрами в начале координат; е) полоса между
прямыми х = 1, x = 2; 2) а) cos1ch3 - i sin1sh3; б) ln2 +
+ iπ(1/6 + 2k); в)
ee
ee
-
-
-
-
55
55
i()
;
4) а) (x
3
- 3x
2
y - 2x
2
+ 2y
2
) +
+ i (3x
2
y - y
3
- 4xy); б)
ee
xy xy
xy ixy
22 22
22
--
+cos( )sin();
в)
tg (th)
tg th
th (tg)
tg th
,
xy
xy
i
yx
xy
1
1
1
1
2
22
2
22
-
+⋅
+
-
+⋅
где
th ;y
yy
yy
=
-
+
-
-
ee
ee
5) а) w =
= 2z - 2i; б) w = 2ie
2iz
; в) не аналитическая; 6) а) -iz
3
+ 5z + ic;
б) z
3
(1 - 2i) + ic.
Рис. 14.1

150
Глава 6
интеГральное исчисление Функции
одной Переменной
15. неоПределенный интеГрал (н.и.)
опорный конспект № 15
15.1. Понятие первообразной и н.и.
∫f(x)dx = F(x) + c — cовокупность первообразных,
F′(x) = f(x), c = const
15.2. Свойства н.и.
1
0
. (∫f(x)dx)′ = f(x).
2
0
. ∫dF(x) = F(x) + c.
3
0
. ∫(f
1
(x) ± f
2
(x))dx = ∫f
1
(x)dx ± ∫f
2
(x)dx.
4
0
. ∫cf(x)dx = c∫f(x)dx.
5
0
. ∫f[ϕ(t)]dϕ(t) = F(ϕ(t)) + c
Частный случай
faxbx
a
Faxb c() ()+= ++
∫
d
1
15.3. Таблица интегралов
1)
xx
x
n
c
n
n
∫
=
+
+
+
d
1
1
,
n ≠ -1;
2)
dx
x
xc
∫
=+ln ;
3) ∫sinxdx = -cosx + c;
4) ∫cosxdx = sinx + c;
5)
dx
x
xc
cos
tg ;
2
∫
=+
6)
dx
x
xc
sin
ctg;
2
∫
=- +
7) ∫tgxdx = -ln|cos x| + c;
8) ∫ctgxdx = ln|sinx| + c;
9)
ax
a
a
c
x
x
∫
=+d
ln
;
10) ∫e
x
dx = e
x
+ c;
11)
dx
x
xc xc
1
2
-
=+=- +
∫
arcsin arccos;
