Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Нуриева С.Н., Дегтярева О.М. Математика в примерах и задачах
Подождите немного. Документ загружается.

61
2
2
2
82
32
2
2
2
42
32
2
22
′
+
=
′
-
⇔
′
+
=
=
′
-
yxy
x .
Производим параллельный перенос системы координат Х′ОY′:
′′
=
′
-
′′
=
′
+
′
-
xx
yy
O
32
2
2
2
32
2
2
2
,
,
,,
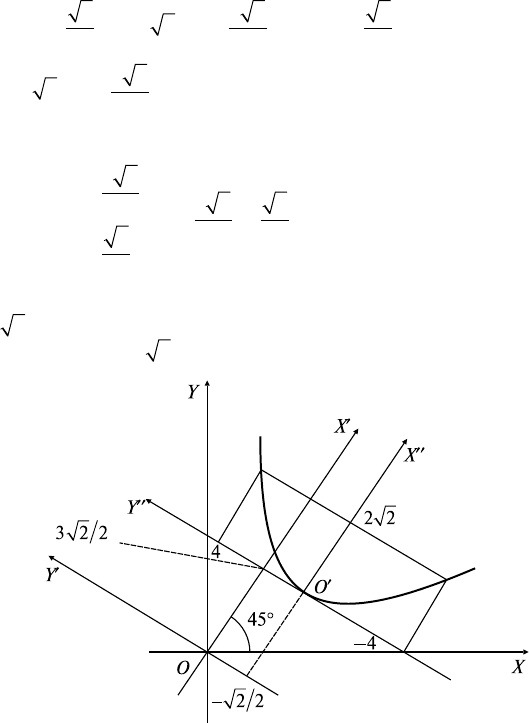
тогда получаем каноническое уравнение в системе Х′′О′Y′′: y′′
2
=
= 4
2
x′′. Парабола симметрична относительно оси O′X′′ и проходит
через точки М
1,2
(2
2
, ±4) в системе X′′O′Y′′ (рис. 4.3).
Задачи для самостоятельного решения
1) Построить кривые: а) 9х
2
+ 25y
2
= 225; б) 4x
2
- 5y
2
= 20;
в) 16х
2
- 9y
2
= -144.
Найти их полуоси, координаты фокусов, эксцентриситеты,
асимптоты (для гиперболы).
2) Построить параболы. Найти параметр р, координаты фокуса:
а) y
2
= -4х; б) x
2
= y/2.
Рис. 4.3
62
3) Найти центр и радиус окружности x
2
+ y
2
- 4x + 6y - 3 = 0.
4) Привести уравнения к каноническому виду и построить кри-
вые:
а) 5x
2
+ 9y
2
- 30x + 18y + 9 = 0; б) 2x
2
- 12x + y + 13 = 0;
в) 5x
2
- 4y
2
+ 30x + 8y + 21 = 0; г) 2y
2
- x - 12y + 14 = 0.
5) Найти канонические уравнения кривых второго порядка с
помощью преобразования поворота и построить кривые: а) x
2
-
- 6xу + y
2
= 8; б) x
2
+ ху + y
2
= 1.
5. аналитическаЯ ГеометриЯ в Пространстве:
Поверхности II ПорЯдка
опорный конспект № 5
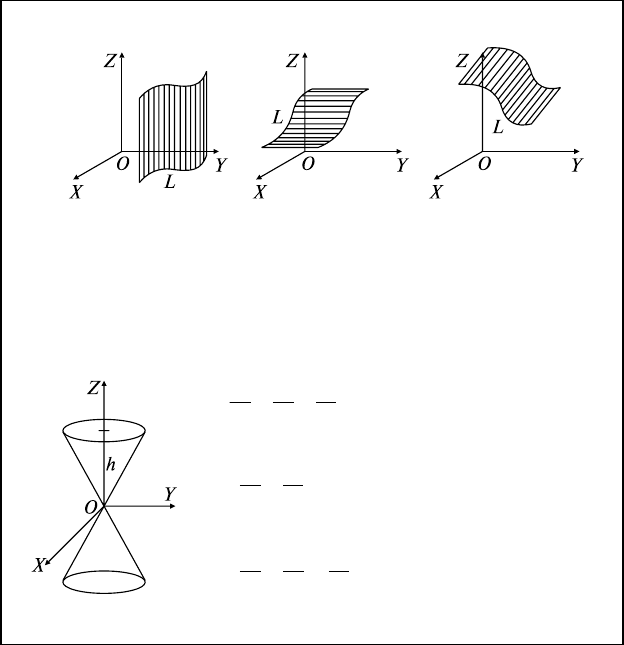
5.1. Цилиндрические поверхности
Направляющая L:
образующие || OZ образующие || OY образующие || OX
L
z
Fxy
:
=
=
0
0
,
(, ),
L
y
Fxz
:
=
=
0
0
,
(,),
L
x
Fxz
:
=
=
0
0
,
(,)
5.2. Конус 2-го порядка
x
a
y
b
z
c
2
2
2
2
2
2
0+-=
x
y
b
z
c
=
-=
0
0
2
2
2
2
,
— прямые
zh
x
a
y
b
h
c
=
-=
,
2
2
2
2
2
2
— эллипсы
63
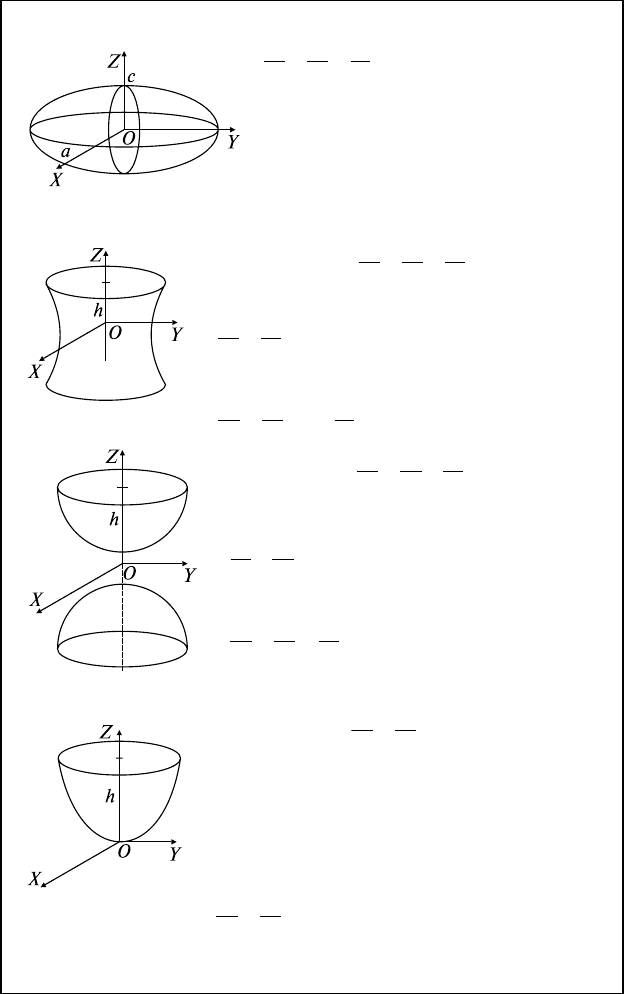
5.3. Эллипсоид
x
a
y
b
z
c
2
2
2
2
2
2
1++=
В сечениях x = h, y = h, z = h — эллипсы.
Частный случай — сфера:
С(x
0
, y
0
, z
0
) — центр,
R — радиус ⇒
⇒ (x - x
0
)
2
+ (y - y
0
)
2
+ (z - z
0
)
2
= R
2
5.4. Гиперболоиды
Однополостный:
x
a
y
b
z
c
2
2
2
2
2
2
1+-=
x
y
b
z
c
=
-=
0
1
2
2
2
2
,
— гипербола
zh
x
a
y
b
z
c
=
+=+
,
2
2
2
2
2
2
1
— эллипсы
Двуполостный:
x
a
y
b
z
c
2
2
2
2
2
2
1+-=-
x
z
c
y
b
=
-=
0
1
2
2
2
2
,
— гипербола
zh
x
a
y
b
h
c
=
+=-
,
2
2
2
2
2
2
1
— эллипсы
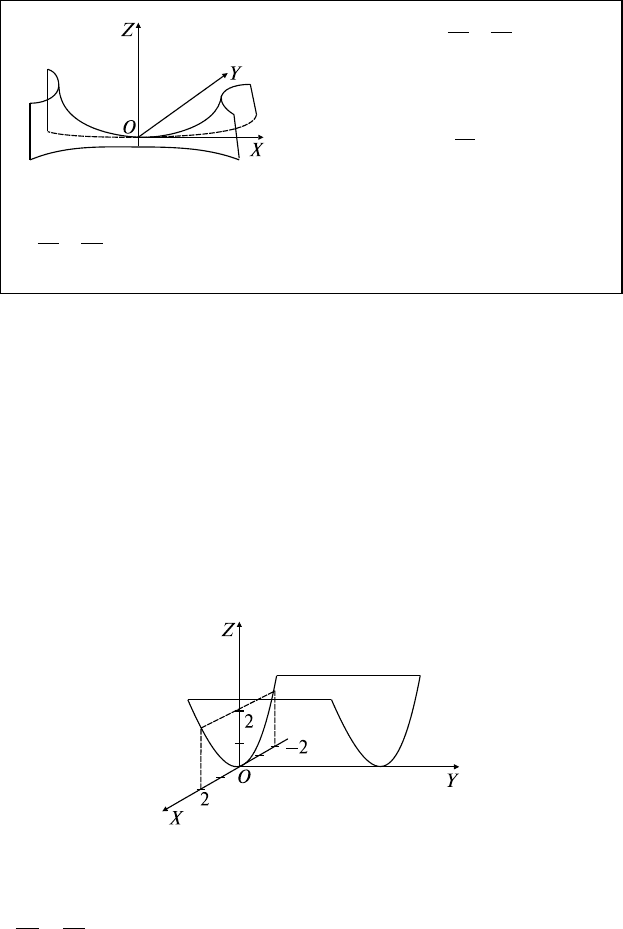
5.5. Параболоиды
Эллиптический:
x
p
y
q
z
22
2+=,
p, q — одного знака
p, q > 0
x
yqz
=
=
0
2
2
,
— парабола
zh
x
p
y
q
h
=
+=
,
22
2
— эллипсы
64
Гиперболический:
x
p
y
q
z
22
2-=,
p, q — одного знака
y
xpz
xh
yq
h
p
z
=
=
=
=-
0
2
2
2
2
2
,
;
,
— пара-
болы
zh
x
p
y
q
h
=
-=
,
22
2
— гиперболы
Задачи к разд. 5
Задача 1. Построить поверхность, заданную уравнением
х
2
= 2z.
Решение: Так как уравнение не содержит у, то оно определяет
цилиндрическую поверхность, образующие которой параллельны
оси OY, а направляющая L:
xz
y
2
2
0
=
=
,
лежит в плоскости XOZ и яв-
ляется параболой. Это параболический цилиндр. Парабола в плос-
кости у = 0 симметрична относительно OZ и проходит через
точки О(0; 0; 0) (вершина), М(±2; 0; 2) (рис. 5.1).
Рис. 5.1
Задача 2. Построить поверхность, заданную уравнением y =
=
xz
22
49
+ .

65
Решение: Применим метод параллельных сечений. В сечениях
плоскостями x = 0, z = 0 имеем параболы:
y
z
x
y
x
z
=
=
=
=
2
2
9
0
4
0
,
,
,
соот-
ветственно. В сечениях плоскостями y = h, h > 0, получаем эллипсы
x
h
z
h
yh
22
49
1+=
=
,
.
Таким образом, данное уравнение является уравнени-
ем эллиптического параболоида, расположенного вдоль оси OY,
с вершиной О(0; 0; 0) (рис. 5.2).
Задачи для самостоятельного решения
1) Найти центр и радиус сферы х
2
+ у
2
+ z
2
- 4x - 2y + 2z - 19 = 0.
2) Построить поверхности, заданные уравнениями:
а)
xyz
222
9259
1++= ;
б)
yz
22
94
1-=;
в)
xy
z
22
2
418
1-+= ;
г)
x
yz
2
22
44
1-+=-;
д) 8х = y
2
+ z
2
;
е)
x
yz
2
2
4
2-=.
Разные задачи
1) Найти уравнение проекции прямой
4710
210
xy z
xyz
-- +=
++-=
,
на
плоскость 4y - z = 0.
Ответ:
xyz+
==
1
17 14
.
Рис. 5.2

66
2) При каком значении параметра λ плоскость x + 2y + 4z - 1 = 0
будет перпендикулярна плоскости, проходящей через точки
М
1
(1, -1, λ), М
2
(2, -1, 1), М
3
(1, 2, 2)?
Ответ: λ = -1.
3) Найти уравнение проекции прямой
xyz
xyz
-+-=
--=
230
20
,
на
плоскость XOZ.
Ответ:
xyz
10
1
1
==
-
.
4) Найти уравнение плоскости, проходящей через линию пере-
сечения плоскостей x + 4y - 3z - 1 = 0, 2x - y + 3z + 1 = 0 и точку
М(1, -1, 0) .
Ответ: x + y = 0.
5) Найти расстояние от точки М(2, 1, 2) до прямой
xyz
xz
-++=
-+=
430
10
,
.
Ответ: 1.
6) Показать, что плоскость 2x + 2y - 3z + 3 = 0 проходит через
линию пересечения плоскостей x - 3y + z - 2 = 0 и 3x - y - 2z + 1 = 0.
7) Даны три точки: А(1; 0; 1); В(-1; 1; 0); С(0; 2; 1). Составить
уравнение плоскости, проходящей через точку М(1, 1, 1) и парал-
лельной плоскости, содержащей треугольник АВС.
Ответ: 2x + y - 3z = 0.
8) Найти проекцию точки М(2, 0, 2) на прямую
yx
yz
-=
-=
0
20
,
.
Ответ: (1; 1; 2).
9) Составить уравнение плоскости, проходящей через точки
М
1
(1; 2; -1), М
2
(1; 3; 1) и перпендикулярной плоскости x + 2y -
- 2z + 3 = 0.
Ответ: 6x - 2y + z - 1 = 0.
10) Найти проекцию точки М(0; 1; 5) на плоскость x - 4z +
+ 3 = 0.
Ответ: (1; 1; 1).
11) Даны точки М
1
(1; 2; -3) и М
2
(3; 0; -1). Найти координаты
точки пересечения прямой М
1
М
2
с плоскостью x + z = 0. Как рас-
положена эта точка относительно точек М
1
, М
2
?
Ответ: (2; 1; -2). Эта точка является серединой отрезка М
1
М
2
.

67
12) Даны точки А(1; 1; 1), В(-1; 0; 2), М(0; 0; 1). АМ — медиана
в треугольнике АВС. Найти уравнение прямой АС.
Ответ:
xyz-
==
1
011
.
13) При каком значении параметра λ угол между плоскостями
λх + у - 7 = 0 и x - λz + 8 = 0 будет равен 60°?
Ответ: λ = 1.
14) Написать уравнение плоскости, проходящей через прямую
xyz-
=
-
=
+1
11
1
2
перпендикулярно к плоскости 6x + y + 5z - 1 = 0.
Ответ: x - y - z - 2 = 0.
15) Показать, что прямые
30
210
xz
yz
-=
++=
,
и
xyz
xy
--=
-+=
880
440
,
компланарны. Пересекаются ли они?
Ответ: Пересекаются.
16) Найти параметрические уравнения прямой, проходящей
через точку М(0; -4; 3) и параллельной прямой
230
10
xyz
xyz
-+-=
+++=
,
,
выбрав параметр t таким образом, чтобы точке М соответствовало
значение t = -1.
Ответ:
xt
yt
zt
=- +
=- +
=+
21
5
32
(),
(),
().
17) Найти уравнения плоскостей, параллельных плоскости 2x -
- 6y - 3z + 1 = 0 и отстоящих от нее на расстояние d = 2.
Ответ: 2x - 6y - 3z + 15 = 0, 2x - 6y - 3z - 13 = 0.
18) Показать, что прямые
320
210
xy
xyz
-+=
+-+=
,
и
xz
yx
--=
-=
10
0
,
пе-
ресекаются, и найти уравнение плоскости, проходящей через эти
прямые.
Ответ: x - 2y + z + 1 = 0.
19) Показать, что прямые
xyz
xy
+-+=
--=
10
230
,
и
xyz
yz
-++=
--=
250
3250
,
параллельны, и написать уравнение плоскости, проходящей через
эти прямые.
Ответ: 10x + 7y - 8z + 5 = 0.

68
20) Найти уравнение перпендикуляра, опущенного из начала
координат на прямую
xyz+
=
+
-
=
4
2
3
10
.
Ответ:
xyz
120
==.
21) Найти точку пересечения прямой
xyz-
=
+
=
-
-
1
1
1
1
3
2
и пер-
пендикуляра, опущенного из начала координат на эту прямую.
Ответ: (2; 0; 1).
22) Написать уравнение плоскости, проходящей через прямую
xyz-
-
=
+
=
3
1
3
20
и точку пересечения прямой
xyz-
-
=
+
=
3
1
3
21
с
плоскостью у = х.
Ответ: 2x + y - 3 = 0.
23) Написать уравнение плоскости, проходящей через ось OZ и
точку пересечения прямой
xyz+
=
+
=
-
2
2
1
12
с плоскостью
ХОY.
Ответ: x - 2y = 0.
ВАРиАнТы КОнТРОЛьнОй РАБОТы
Вариант № 1
1. Найти уравнение прямой L, проходящей через т. М
1
(4; 3) и
через точку пересечения прямых L
1
: 2x + 5y - 8 = 0, L
2
: x - 3y + 4 =
= 0.
Ответ: 17x - 40y + 52 = 0.
2. Найти угол между плоскостями G
1
: 4x - 5y + 3z - 1 = 0, G
2
:
x - 4y - z + 9 = 0.
Ответ: θ = arccos0,7.
3. Привести уравнение к каноническому виду и построить кри-
вую 16x
2
+ 25y
2
+ 32x - 100y - 284 = 0.
Ответ:
′
+
′
=
xy
22
25 16
1.
4. Построить поверхность, заданную уравнением
xy
22
49
1-=.
Ответ: Гиперболический цилиндр.
69
Вариант № 2
1. Через точку М
0
(2; -5; 3) провести прямую, параллельную
прямой
2310
54 70
xy z
xyz
-+ -=
+--=
,
.
Ответ:
xyz-
-
=
+
=
-2
11
5
17
3
13
.
2. Вычислить угол между прямыми: L
1
: 2x + y - 5 = 0, L
2
: 6x -
- 2y + 7 = 0.
Ответ: θ = 3π/4.
3. Привести уравнение к каноническому виду и построить кри-
вую 4x
2
- 8x - y + 7 = 0.
Ответ:
′
=
′
xy
2
1
4
.
4. Построить поверхность, заданную уравнением
-++=
x
yz
2
22
4
1.
+ z
2
= 1.
Ответ: Однополостный гиперболоид.
Вариант № 3
1. Найти ординату точки С, лежащей на прямой, проходящей
через точки А(-8; -6), В(-3; -1), если абсцисса точки С: х = 5.
Ответ: y = 7.
2. Написать уравнение плоскости, проходящей через т. М(2;
1; 4) и перпендикулярной прямой
xyz
xy
+-=
-+=
0
220
,
.
Ответ: x + 2y + 3z - 16 = 0.
3. Привести уравнение к каноническому виду и построить кри-
вую 16x
2
- 9y
2
- 64x - 18y + 199 = 0.
Ответ:
′
-
′
=
yx
22
16 9
1.
4. Построить поверхность, заданную уравнением
x
yz
=+
22
49
.
Ответ: Эллиптический параболоид.
70
расчетное задание
теоретические вопросы
1. Общее уравнение прямой на плоскости. Особые случаи об-
щего уравнения.
2. Уравнение прямой с угловым коэффициентом. Геометриче-
ский смысл параметров k и b.
3. Общее уравнение плоскости. Геометрический смысл пара-
метров А, В, С. Особые случаи общего уравнения плоскости.
4. Канонические и параметрические уравнения прямой в про-
странстве. Направляющий вектор прямой.
5. Общие уравнения прямой. Их геометрический смысл. Вы-
числение направляющего вектора прямой, заданной общими урав-
нениями.
6. Определение эллипса. Его каноническое уравнение. Геомет-
рический смысл параметров a, b, c и основное соотношение между
ними.
7. Определение гиперболы и ее асимптот. Каноническое урав-
нение гиперболы и уравнения ее асимптот. Геометрический смысл
параметров a, b, c и основное соотношение между ними.
8. Определение параболы. Ее канонические уравнения. Геомет-
рический смысл параметрa р.
9. Формулы параллельного переноса осей координат на плос-
кости.
задания
Ниже используются следующие обозначения: αβγδ — цифры
номера группы, n — номер студента по списку, λ - 1 = ](n + γ + δ)/5[;
µ - 1 = ](n + β)/4[; ν - 1 = ](n + α)/3[, где ]...[ — остаток от деления.
1. Даны точка М
0
(3 + λ + ν; 3 + µ - ν) и прямая L: (λ + 1)х +
+ (µ + 1)у = 2 - λ
2
- µ
2
+ (λ - µ)ν.
Требуется:
а) найти расстояние d от точки М
0
до прямой L; б) написать
уравнение прямой L
1
, проходящей через точку М
0
и перпендику-
лярной прямой L; в) найти проекцию Р точки М
0
на прямую L;
г) проверить на чертеже результат пункта в).
2. Даны две точки: М
1
(ν - 3; λ - 3µ + 6); М
2
(ν - 1; λ - µ + 1) и
прямая L: (2µ - 3)х - 2у + 2λ - 5 + ν(3 - 2µ) = 0.
