Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Нуриева С.Н., Дегтярева О.М. Математика в примерах и задачах
Подождите немного. Документ загружается.


31
()()() .
abbcca abc+++=2
56) Установить, образуют ли векторы
abc,,
базис в простран-
стве R
3
, если
a
= {3; -2; 1},
b
= {2; 1; 2},
c
= {3; -1; 2}.
57) Показать, что векторы
aijk=- ++32,
bi jk=--23 4 ,
cijk=- ++3126
компланарны. Разложить
c
по векторам
a
и
b
.
58) Показать, что точки А(2; -1; -1); В(1; 2; 1); С(2; 3; 0);
D(1; 6; 2) лежат в одной плоскости.
59) При каком λ векторы
a
= {λ; 3; 1},
b
= {5; -1; 2},
c
= {-1; 5; 4}
будут компланарны?
60) Найти объем параллелепипеда, построенного на векторах
ai j=+34,
bjk=- +3 ,
cjk=+25.
61) Вычислить объем и высоту треугольной пирамиды АВСD,
опущенную из вершины D, если А(1; 1; 1), В(2; 0; 2), С(2; 2; 2),
D(3; 4; -3).
Задачи к разд. 2.8
Задача 1. Найти базис и размерность подпространства решений
однородной системы линейных уравнений
32 40
23 20
4490
1234
1234
12 34
xxxx
xx xx
xx xx
-+-=
--+=
-+ -=
,
,
.
Решение: Применяя метод Гаусса, найдем общее решение сис-
темы:
xxx
xxx
214
314
8
7
4
5
7
2
=-
=- +
,
,
где x
1
, x
4
принимают любые действительные значения. Рассмотрим
два частных решения u и v, положив x
1
= 1, x
4
= 0, затем x
1
= 0, x
4
= 1:
u
= (1; 8/7; -5/7; 0),
v
= (0; -4; 2; 1). Любое решение тогда представ-
ляется в виде x = x
1
u
+ x
4
v
, что проверяется подстановкой координат
u
и
v
. Таким образом, мы можем утверждать, что векторы
u
и
v
об-
разуют базис, если докажем их линейную независимость. Послед-
няя следует из того, что равенство x
1
u
+ x
4
v
= 0 может иметь место
32
лишь при x
1
= 0, x
4
= 0. По определению размерность такого линей-
ного пространства решений системы равна двум.
Задача 2. Показать, что векторы
x
1
= (1; 2,1; 2),
x
2
= (-1; 3; 2,1),
x
3
= (-13; -1,2; -11) линейно зависимы. Найти эту зависимость.
Решение: Составим линейную комбинацию λ
1
x
1
+ λ
2
x
2
+ λ
3
x
3
= 0.
Это векторное уравнение эквивалентно следующей системе урав-
нений:
λλ λ
λλλ
λλλ
λλ λ
12 3
123
123
12 3
13 0
23 0
220
2110
-- =
+-=
++=
+- =
,
,
,
.
Решая ее методом Гаусса, находим: λ
1
= 8λ
3
; λ
2
= -5λ
3
. Состав-
ленная линейная комбинация примет вид 8x
1
- 5x
2
+ x
3
= 0. Это
равенство и доказывает линейную зависимость данной системы
векторов.
Задача 3. Проверить ортогональность векторов
e
1
= {1; -2; 1; 3},
e
2
= {2; 1; -3; 1} и дополнить их до ортогонального базиса в R
4
.
Решение:
ee
12
⋅
= 2 - 2 + 3 - 3 = 0. Пусть
e
3
= {α
1
; α
2
; α
3
; α
4
}, тогда
из
ee
13
⋅
= 0;
ee
23
⋅
= 0 получаем систему
αααα
αα αα
1234
12 34
230
23 0
-++=
+- +=
,
.
Находим ее любое решение, это и будет
e
3
, например
e
3
= {-4; 2;
-1; 3}. Пусть
e
4
= {β
1
; β
2
; β
3
; β
4
}, тогда из
e
1
⋅
e
4
= 0,
e
2
⋅
e
4
= 0,
e
3
⋅
e
4
= 0
получаем систему
ββββ
ββ ββ
ββββ
1234
12 34
1234
230
23 0
42 30
-++=
+- +=
-+ -+ =
,
,
.
Находим любое ее решение, это и будет
e
4
, например
e
4
=
= {2; 4; 3; 1}.
Задачи для самостоятельного решения
62) Образуют ли следующие векторы базис пространства R
3
?
а)
x
1
= (3; 0; 2),
x
2
= (7; 0; 9),
x
3
= (4; 1; 2);
б)
x
1
= (1; 1; 0),
x
2
= (3; 0; 1),
x
3
= (5; 2; 1).

33
63) Показать, что векторы
e
1
,
e
2
,
e
3
образуют базис, и найти ко-
ординаты
x
в этом базисе:
e
1
= (1; 1; 1),
e
2
= (1; 1; 2),
e
3
= (1; 2; 3),
x
=
= (6; 9; 14).
64) Найти базис и размерность подпространства решений од-
нородной системы линейных уравнений:
а)
2453 0
36 42 0
4817 11 0
1234
1234
12 34
xxxx
xx xx
xx xx
-++=
-++=
-+ +=
,
,
;
б)
35 20
4750
40
2960
123
123
12 3
123
xx x
xxx
xx x
xxx
++=
++=
+- =
++=
,
,
,
.
65) Найти угол между векторами
a
= (1; 0; 1; 0),
b
= (1; 1; 1; 1).
66) Проверить ортогональность векторов в евклидовом про-
странстве R
n
и дополнить до ортогональных базисов:
а)
e
1
= (2/3; 1/3; 2/3),
e
2
= (1/3; 2/3; -2/3), n = 3;
б)
e
1
= (1; 1; 1; 2),
e
2
= (1; 2; 3; -3), n = 4.
Задачи к разд. 2.9
Задача 1. Найти собственные значения и собственные векторы
линейного преобразования, заданного матрицей
A =
-
-
-
320
210
15 74
.
Решение: Характеристическое уравнение
--
--
--
=⇔ -++=
320
21 0
15 74
04 210
2
λ
λ
λ
λλ λ()().
Таким образом, λ
1
= 4, λ
2
= λ
3
= -1 — спектр матрицы А. Соб-
ственные векторы находим, решая систему
() ,
() ,
() .
-- +=
-+-=
-+-=
320
21 0
15 74 0
12
12
12 3
λ
λ
λ
xx
xx
xx x

34
При λ
1
= 4 она имеет вид
-+ =
-- =
-=
72 0
23 0
15 70
12
12
12
xx
xx
xx
,
,
.
Тогда первый собственный вектор получается равным
u
=
= k(0; 0; 1), где k — любое действительное число (k ≠ 0). Второй
собственный вектор определяется из системы при λ = -1:
-+ =
-+ =
-+=
22 0
22 0
15 75 0
12
12
123
xx
xx
xxx
,
,
.
Ее общее решение x
1
= x
2
, x
3
= -
8
5
x
2
, т.е.
v
= l(1; 1; -8/5), где l —
любое действительное число.
Задача 2. Найти диагональную форму матрицы А и новый базис,
если
A =
111
111
111
.
Решение: Матрица А симметрическая, поэтому ее можно диаго-
нализировать. Находим спектр матрицы А: λ
1
= 3, λ
2
= λ
3
= 0, затем
собственные векторы, решая системы
-++=
-+=
+- =
20
20
20
123
123
12 3
xxx
xxx
xx x
,
,
;
x
1
+ x
2
+ x
3
= 0.
Решение первой системы x
1
(1; 1; 1), второй — (-(x
2
+ x
3
); x
2
; x
3
).
Тогда можно взять в качестве базиса
e
1
= (1; 1; 1),
e
2
= (-1; 1; 0),
e
3
=
(-1; 0; 1). Диагональная форма матрицы
300
000
000
.
Задача 3. Привести квадратичную форму f(x
1
, x
2
) = 3x
1
2
+ 10x
1
x
2
+
+ 3x
2
2
к каноническому виду.
Решение: Матрица квадратичной формы
A =
35
53
.
Находим ее
собственные значения:
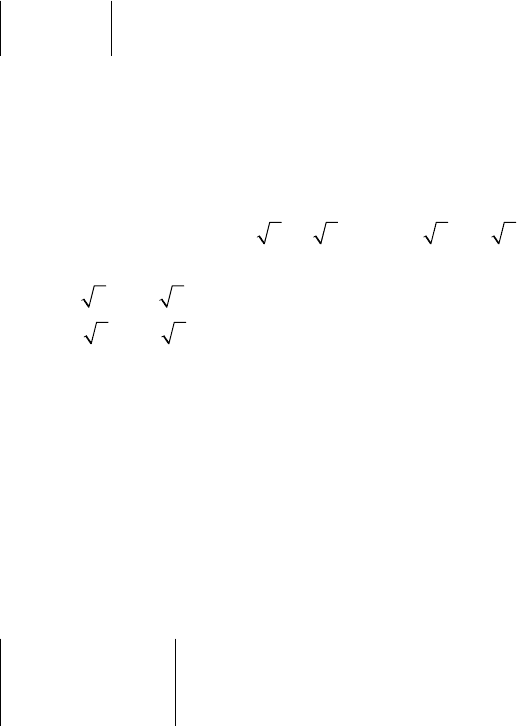
35
35
53
082
12
-
-
=⇒ ==-
λ
λ
λλ,.
Собственные векторы получаются из систем:
-+ =+=
-=
55 05 50
55 0
12 12
12
uu uu
uu
,,
.
Решение первой u
1
= u
2
, второй — u
1
= -u
2
, собственные векторы
a
1
= u
1
(1; 1),
a
2
= u
1
(1; -1). Ортогональный базис (1; 1); (1; -1); орто-
нормированный базис
′
e
1
= (1/
2
; 1/
2
);
′
e
2
= (1/
2
; -1/
2
). Таким
образом, преобразованием
xx x
xx x
11 2
21 2
22
22
=
′
+
′
=
′
-
′
//
//
,
квадратичная форма приводится к виду f(x
1
, x
2
) = 8(x′
1
)
2
- 2(x′
2
)
2
.
Задача 4. Проверить, является ли квадратичная форма f(x
1
, x
2
,
x
3
) = 6x
1
2
+ 5x
2
2
+ 7x
3
2
- 4x
1
x
2
+ 4x
1
x
3
положительно определенной.
Решение: Матрица квадратичной формы
A =
-
-
622
250
207
.
Собственные значения находим из характеристического урав-
нения
622
25 0
207
0369
123
--
--
-
=⇒ ===
λ
λ
λ
λλλ,,,
т.е. квадратичная форма является положительно определенной.
Задачи для самостоятельного решения
67) Найти матрицу преобразования суммы следующих линей-
ных преобразований:
′
=+
′
=+
′′
=-
′′
=-
xxx
xxx
xxx
xx x
112
212
112
21 2
35
47
78
5
,
;
,
.
68) Показать, что данное линейное преобразование невырож-
денное, и найти обратное преобразование:
36
а)
′
=-+
′
=+ -
′
=+-
xxxx
xx xx
xxxx
1123
21 23
3123
23
54
43
,
,
;
б)
′
=-+
′
=- +
′
=-+
xxxx
xx xx
xxxx
1123
21 23
3123
243
24
35
,
,
.
69) Даны два линейных преобразования. Найти преобразова-
ние, выражающее через x″
1
, x″
2
, x″
3
через x
1
, x
2
, x
3
:
а)
′
=-+
′
=-
′
=-
xxxx
xx x
xxx
1123
21 2
323
53
2
73
,
,
;
б)
′′
=
′
+
′
′′
=
′
-
′
′′
=
′
xxx
xx x
xx
113
22 3
31
2
3
2
,
,
.
70) Найти собственные значения и собственные векторы ли-
нейных преобразований:
а)
212
533
102
-
-
--
;
б)
--
1212
043
056
;
в)
720
262
025
-
--
-
.
71) Найти диагональную форму матрицы и новый ортонорми-
рованный базис (базис определен неоднозначно):
а)
11 28
2210
8105
-
-
;
б)
1784
8174
4411
-
--
-
.
72) Привести квадратичные формы к каноническому виду и
найти соответствующие преобразования:
а) f(x
1
, x
2
) = 9x
1
2
- 4x
1
x
2
+ 6x
2
2
;
б) f(x
1
, x
2
, x
3
) = 11x
1
2
+ 5x
2
2
+ 2x
3
2
+ 16x
1
x
2
+ 4x
1
x
3
- 20x
2
x
3
.
73) Проверить, являются ли квадратичные формы положитель-
но определенными:
а) x
1
2
+ x
2
2
+ x
3
2
+ 4x
1
x
2
+ 4x
1
x
3
+ 4x
2
x
3
;
б) 17x
1
2
+ 14x
2
2
+ 14x
3
2
- 4x
1
x
2
- 4x
1
x
3
- 8x
2
x
3
.
74) При каких значениях k квадратичная форма Q(x
1
, x
2
, x
3
)
является положительно определенной?
а) Q(x
1
, x
2
, x
3
) = kx
1
2
+ 2x
2
2
+ 3x
3
2
;
б) Q(x
1
, x
2
, x
3
) = 3x
1
2
- kx
2
2
- 4x
1
x
2
.
37
Разные задачи
1. Образует ли линейное пространство заданное множество,
в котором определены сумма любых двух элементов a и b и произ-
ведение любого элемента a на любое число α?
1.1. Множество всех векторов трехмерного пространства, ко-
ординаты которых целые числа, сумма
ab+
, произведение
α
a
.
Ответ: Нет.
1.2. Множество всех векторов, лежащих на одной оси: сумма
ab+
, произведение
α
a
.
Ответ: Да.
1.3. Множество всех векторов, являющихся линейной комби-
нацией данных векторов x
1
, x
2
, ..., x
n
из R
n
.
Ответ: Да.
2. Вектор
x
, перпендикулярный к векторам
a
= {3; 2; 2} и
b
= {18; -22; -5}, образует с осью OY тупой угол. Найти его коорди-
наты, если |x| = 14.
Ответ: {-4; -6; 12}.
3. Для системы векторов
x
1
= {1; 2; 1; 2};
x
2
= {-1; 3; 2; 1};
x
3
=
= {-13; -1; 2; -1} найти все базисы.
Ответ: {
x
1
;
x
2
} и {
x
2
;
x
3
}.
4. Даны векторы
a
= {3; -5; 2};
b
= {4; 5; 1};
c
= {-3; 0; -4} в неко-
тором базисе. Показать, что векторы
a
,
b
,
c
образуют базис, и раз-
ложить вектор
u
= {4; 25; 10} по этому базису.
Ответ: {-1; 4; 3}.
5. Определить длины диагоналей параллелограмма, построен-
ного на векторах
a
= 2
m
+
n
и
b
=
m
- 2
n
, если |
m
| = |
n
| = 1,
(,)
mn
= 60°.
Ответ:
7
,
13
.
6. Доказать, что
ab bc ca×=×=×
, если
abc++= 0.
7. Вектор
a
составляет с координатными осями OY и OZ углы
β = 120° и γ = 45°. Вычислить его координаты при условии, что
|
a
| = 6.
Ответ:
a
1
= {3; -3; 3
2
},
a
2
= {-3; -3; 3
2
}.
8. Векторы
a
= {2; 1; -2} и
b
= {-3; -2; 6} приложены к одной
точке. Определить координаты вектора
c
, направленного по бис-
сектрисе угла между векторами
a
и
b
, при условии |
c
| = 5
42
.
Ответ:
c
= {25; 5; 20}.

38
9. Вычислить объем параллелепипеда, построенного на векто-
рах
mabc=++
,
nabc=-+
,
pabc=--
.
Ответ: V = 4
abc
.
10. Доказать, что если для матриц А и В оба произведения АВ и
ВА существуют, причем АВ = ВА, то матрицы А и В квадратные и
имеют одинаковый порядок.
11. Доказать, что сумма характеристических чисел матрицы А
равна ее следу (т.е. сумме элементов главной диагонали), а произ-
ведение характеристических чисел равно определителю |A|.
12. Вычислить косинус тупого угла между медианами, прове-
денными из вершин острых углов равнобедренного треуголь-
ника.
Ответ: сos ϕ = -4/5.
13. Зная векторы
a
и
b
, на которых построен параллелограмм,
выразить через них вектор, совпадающий с высотой параллело-
грамма, перпендикулярной к стороне
a
.
Ответ:
h
ab
a
ab=
⋅
-
2
().
14. Вычислить объем параллелепипеда, построенного на век-
торах
a
= 3
m
+ 5
n
,
b
=
m
- 2
n
,
c
= 2
m
+ 7
n
, где |
m
| = 0,5; |
n
| = 3,
(,)
mn
=
= 135°.
Ответ: V = 0.
15. Доказать, что смешанное произведение трех векторов, из
которых два коллинеарны, равно нулю.
16. Вектор
x
, коллинеарный вектору
a
= (6; -8; -7,5), образует
острый угол с осью OZ. Зная, что |
x
| = 50, найти его координаты.
Ответ:
x
= (-24; 32; 30).
17. Доказать, что вектор
pb
aa b
a
=-
⋅()
2
перпендикулярен к век-
тору
a
.
18. Определить геометрическое место концов переменного век-
тора
x
, если его начало находится в данной точке А и вектор
x
удовлетворяет условию
x
⋅
a
= α, где вектор
a
и число α заданы.
Ответ: Плоскость, перпендикулярная к оси вектора
a
и отсека-
ющая на нем отрезок, величина которого, считая от точки А, равна
α/|
a
|.
39
19. Объем тетраэдра V = 5, три его вершины находятся в точках
А(2; 1; -1), В(3; 0; 1), С(2; -1; 3). Найти координаты четвертой вер-
шины D, если известно, что она лежит на оси OY.
Ответ: D
1
(0; 8; 0), D
2
(0; -7; 0).
20. Векторы
a
и
b
образуют угол ϕ = 60°, причем |
a
| = 5, |
b
| = 8.
Определить |
a
+
b
| и |
a
-
b
|.
Ответ:
1297,
.
21. Вычислить длину
s
= α
a
+ β
b
+ γ
c
, если
a
,
b
,
c
взаимно пер-
пендикулярны.
Ответ:
sabc=++αβγ
222
.
22. Даны векторы
p
,
q
,
r
,
n
. Доказать, что векторы
a
=
p
×
n
;
b
=
=
q
×
n
;
c
=
r
×
n
компланарны.
23. Точка М расположена вне прямоугольника АВСD. Доказать:
MA MC MB MD
⋅=⋅ ,
MA MC MB MD
22 22
+=+ .
24. Доказать коллинеарность векторов
a
-
d
,
b
-
c
, если
a
×
b
=
=
c
×
d
,
a
×
c
=
b
×
d
.
25. Найти проекцию вектора
s
= (4; -3; 2) на ось, составляющую
с осями координат равные острые углы.
Ответ:
3
.
26. Векторы
a
,
b
,
c
имеют равные длины и образуют попарно
равные углы. Найти координаты вектора
c
, если
a
=
i
+
j
,
b
=
=
j
+
k
.
Ответ: (-1/3; 4/3; -1/3) или (1; 0; 1).
27. Сила, определяемая вектором
R
= {1, -8, -7}, разложена по
трем направлениям, одно из которых задано вектором
a
= 2
i
+
+ 2
j
+
k
. Найти составляющую силы
R
в направлении вектора
a
.
Ответ: (-14/3; -14/3; -7/3).
28. Зная векторы
a
и
b
, на которых построен параллелограмм,
выразить через них вектор, перпендикулярный к плоскости парал-
лелограмма, длина которого равна r.
Ответ:
ab
ab
⋅
⋅
⋅r.
29. Доказать, что векторы
a
,
b
,
c
, удовлетворяющие условию
a
×
b
+
b
×
c
+
c
×
a
= 0, компланарны.
30. Показать, что если
a
⊥
b
,
a
⊥
c
, то
a
× (
b
×
c
) = 0.

40
31. Доказать, что |
abc
| ≤ |
a
||
b
||
c
|. В каком случае здесь может
иметь место знак равенства?
32. Доказать тождество
a
× (
b
×
c
) =
b
(
a
c
) -
c
(
a
b
).
33. Проверить справедливость равенства (
a
×
b
) ×
c
+ (
b
×
c
) ×
×
a
+ (
c
×
a
) ×
b
= 0.
34. Изменится ли сумма
s
компланарных векторов, если все
слагаемые векторы будут повернуты в одном и том же направлении
на один и тот же угол?
Ответ: |
s
| не изменится.
35. Найти равнодействующую пяти компланарных сил, равных
по величине и приложенных к одной и той же точке, зная, что углы
между каждыми двумя последовательными силами равны 72°.
Ответ: 0.
36. Даны вещества: СН
4
, СН
2
О, О
2
, Н
2
О. Используя запись А =
= βВ, где
AB=
=
=
CH
CH O
O
HO
H
C
O
4
2
2
2
,,β
410
211
002
201
,
найти стехиометрические коэффициенты α
i
, i =
14,
, реакции вида
α
1
СН
4
+ α
2
СН
2
О + α
3
О
2
+ α
4
Н
2
О = 0.
Ответ: Возможна одна независимая реакция СН
4
+ О
2
=
= СН
2
О + Н
2
О.
Указание: Представить реакцию в матричном виде (α
1
α
2
α
3
α
4
) ×
× А = 0 и перейти к системе линейных алгебраических уравне-
ний.
37. Исходные вещества Н
2
, Br
2
, продукт HBr.
а) взяв (см. задачу 36)
AB=
=
H
H
Br
Br
HBr
H
Br
2
2
,,
записать атомную
матрицу β;
б) определить, используя запись А = βВ, результатом каких ста-
дий является брутто-реакция Н
2
+ Br
2
= 2HBr.
Ответ:
Br Br Br HHBr HH Br HBrBr
22 2
2 ,, .++++
