Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Нуриева С.Н., Дегтярева О.М. Математика в примерах и задачах
Подождите немного. Документ загружается.


21
2.7. Смешанное произведение
abcabcabc
aaa
bbb
ccc
xyz
xyz
xyz
=×⋅=(),
Свойства:
1
0
.
() ().
abcabc×⋅=⋅ ×
2
0
.
abcbac=- .
3
0
.
abcbca cab==.
4
0
. Объем параллелепипеда, построенного на
a
,
b
,
c
:
Vabc
пар
=
;
объем треугольной пирамиды
Vabc
пир
= 6.
5
0
.
a
,
b
,
c
— компланарны ⇔
a
b
c
= 0
2.8. Линейное пространство. Евклидово пространство R
n
RR
n
ni
ain== ∈={{,,..., }; ,,}
αα αα
12
1
— n-мерное векторное
пространство
⇔
a
+
b
= {α
1
+ β
1
, α
2
+ β
2
, ..., α
n
+ β
n
},
λ
a
= {λα
1
, λα
2
, ..., λα
n
}, λ ∈ R, ∀
a
,
b
∈ R
n
.
Базис в R
n
— ∀ линейно независимые
e
1
,
e
2
,
...,
e
n
∈ R
n
.
Пусть базис
e
1
= (1, 0, ..., 0),
e
2
= (0, 1,..., 0) ,...,
e
n
= (0, 0, ..., 1),
a
⋅
b
= α
1
β
1
+ α
2
β
2
+ ... + α
n
β
n
⇔ R
n
— n-мерное евклидово про-
странство,
a
n
=+++αα α
1
2
2
22
... .
2.9. Линейные преобразования. Собственные значения и собствен-
ные векторы. Квадратичные формы в R
n
А — линейное преобразование в
RR
nn
xAxxx⇔
′
=
′
∈
,, ,
Ax yAxAy() ,
+= +
Ax Ax xy
n
() ,,.λλ λ
=∀∈∈RR
ee e
n12
,,...,
— базис в R
n
⇒ A = (a
ij
), i,
jn= 1,.
x
— собственный вектор
Ax⇔
:
Ax x
=λ,
λ ∈ R — собственное
значение
det(A - λE) = 0 — характеристическое уравнение А.
А — самосопряженный в евклидовом пространстве R
n
⇔
⇔
Ax yxAy
⋅=⋅
⇒ в ортонормированном базисе A = (a
ij
) = (a
ji
),
i,
jn=⇒∃1,
ортонормированный базис из собственных векторов:
матрица оператора А имеет диагональную форму
22
Квадратичная форма f(x
1
, x
2
, ..., x
n
) =
axx
ij
j
n
i
n
ij
==
∑∑
11
,
a
ij
= a
ji
,
i,
jn= 1,,
A = (a
ij
) — ее матрица, приводится к каноническому виду
λ
i
i
n
i
x
=
∑
1
2
,
λ
i
— собственные значения А
Задачи к разд. 2.1, 2.2
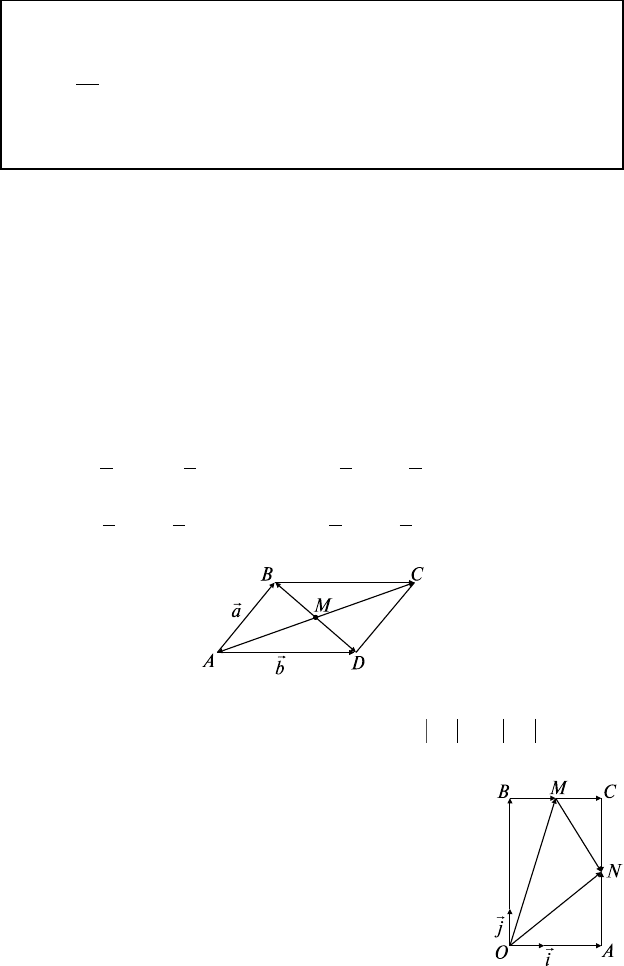
Задача 1. В параллелограмме АВСD обозначены
AB a
= ,
AD b
= .
Выразить через векторы
a,
b
векторы
MA
,
MB
,
MC
,
MD
,
если М —
точка пересечения диагоналей (рис. 2.1).
Решение: По определениям сложения и вычитания
AC ab
=+,
BD ba
=-.
Так как диагонали в точке М делятся пополам, то, ис-
пользуя умножение вектора на число, имеем:
MA AC ab MC AC ab
=- =- +==+
1
2
1
2
1
2
1
2
(),(),
MB BD ab MD BD ba
=- =- ==-
1
2
1
2
1
2
1
2
(),().
Рис. 2.1
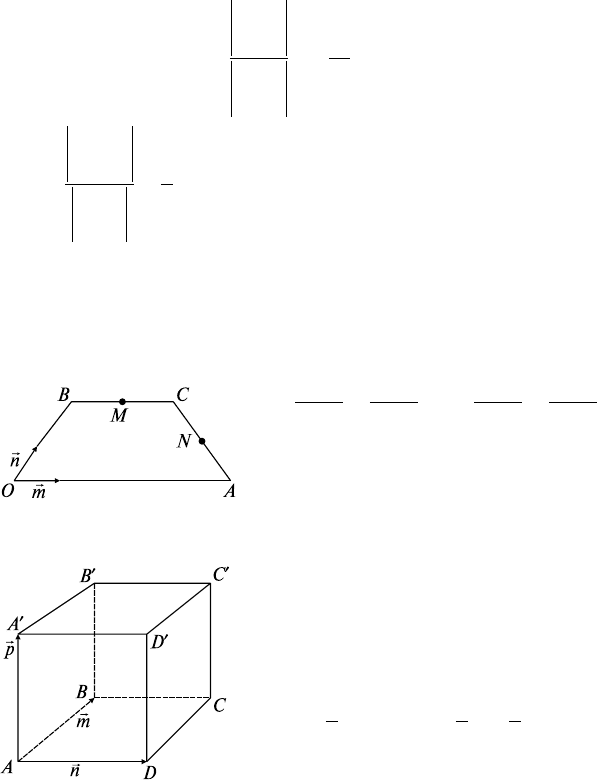
Задача 2. В прямоугольнике ОАСВ заданы
OA
= 3,
OB
= 4,
М —
середина ВС, N — середина АС. Выразить
OM
,
ON
,
MN
через еди-
ничные векторы
i
,
j
в направлении
OA
,
OB
соот-
ветственно (рис. 2.2).
Решение: По определению умножения вектора
на число
OA i
= 3 ,
OB j
= 4 ,
BM MC i
==15,,
NC AN j
==2 .
По определению сложения
OM OB BM ji
=+ =+415,,
ON OA AN ij
=+ =+32,
ON OA AN ij
=+ =+32,
MN
=
MC CN ij
+=-15 2,.
Рис. 2.2
23
Задача 3. Известны координаты векторов в некотором базисе
a =-{; },21
b = {; },32
c =-{;}.14
Разложить вектор
c
по базису
a,
b.
Решение: В базисе
a,
b
вектор
cab=+αβ,
где α, β неизвестны.
Запишем равенство через координаты: {-1; 4} = {2α + 3β, -α + 2β}.
Имеем систему для нахождения α, β:
23 1
24
13
42
23
12
14
7
2
αβ
αβ
α
+=-
-+ =
⇒=
-
-
=- =-
,
,
;
β=
-
-
-
==⇒=-+
21
14
23
12
7
7
12
cab.
Задачи для самостоятельного решения
1) Проверить аналитически и геометрически векторные тожде-
ства:
a
ba ab
a
ab ab
+
-
=
+
-
+
=
-
22 22
;.
2) В равнобедренной трапеции
ОАСВ угол ВОА = 60°, |OB| = |BC| = |CA| =
= 2, М и N — середины сторон ВС и АС
соответственно (рис. 2.3). Выразить
AC
,
OM
,
ON
,
MN
через единичные векторы
m,
n
в направлении
OA
,
OB
соответственно.
3) В параллелепипеде АВСDA′B′C′D′
обозначены:
AB m
= ;
AD n
= ;
AA p
′
=
(рис. 2.4). Построить векторы
mn p++;
mn p++
1
2
;
mn p+-;
1
2
1
2
mnp++.
4) В треугольнике АВС обозначены
AB a
= ,
CA b
= .
Выразить через
a,
b
век-
торы, совпадающие с медианами тре-
угольника.
Рис. 2.3
Рис. 2.4

24
5) Векторы
a,
b
взаимно перпендикулярны, причем
a = 5,
b = 12.
Определить
ab+ ;
ab- .
6) Известно, что
a = 13;
b = 19;
ab+=24.
Найти
ab- .
7) Три силы
M,
N,
P,
приложенные к одной точке, имеют вза-
имно перпендикулярные направления. Определить величину их
равнодействующей
R,
если
M = 2H;
N = 10 H;
P = 11H.
8) Пусть в некотором базисе
a =-{; ;};123
b = {; ;}.021
Найти
32
ab+ ,
ab- 4 .
9) На плоскости даны два вектора
p =-{; };23
q = {; }.12
Найти
разложение вектора
a = {; }94
по базису
p,
q.
10) Даны три вектора
p =-{; ;};321
q =- -{;;};11 2
r =-{;;}.21 3
Най-
ти разложение вектора
c =-{; ;}11 65
по базису
pqr,,.
11) Даны четыре вектора
a = {;;};210
b =-{; ;};112
c =-{; ;};22 1
d =-{; ;}.37 7
Определить разложение каждого из этих четырех век-
торов, принимая в качестве базиса три остальных.
12) Пусть в некотором базисе
a =-{; ;};λ 12
b = {, ,}.36µ
Найти λ,
µ, при которых
a,
b
коллинеарны.
13) Даны три некомпланарных вектора
abc,,.
Найти λ и µ, при
которых векторы
λµ
abc++;
abc++λµ
коллинеарны.
Задачи к разд. 2.3, 2.4
Задача 1. Определить точку В, которая является концом векто-
ра
a
= {4; -3; 1}, если его начало — точка А(3; 1; -2).
Решение:
a
= {4; -3; 1} = {x
B
- 3; y
B
- 1; z
B
+ 2} ⇒ x
B
= 4 + 3 = 7, y
B
=
= -3 + 1 = -2, z
B
= 1 - 2 = -1 ⇒ B(7; -2; -1).
Задача 2. Даны точки А(-1; 2; 3), В(0; 3; 5), С(1; -2; 3). Найти
длину и направляющие косинусы вектора
aABAC=-3 .
Решение: Найдем координаты векторов:
AB
= {1; 1; 2},
AC
= {2; -4; 0};
a
= {1 - 3 ⋅ 2; 1 - 3 ⋅ (-4); 2 - 3 ⋅ 0} =
= {-5; 13; 2} ⇒
a =++=25 1694 198,
cos,α=
-5
198
cos,β=
13
198
cos.γ=
2
198
Задача 3. Вектор
a
составляет с координатными осями ОХ и ОY
углы α = 60°, β = 120°. Вычислить его координаты при условии, что
a = 2.

25
Решение: Воспользуемся свойством 1
0
проекции вектора на ось,
так как прямоугольные координаты вектора являются его проек-
циями на оси координат:
aa
X
==⋅=
cos;α 2
1
2
1
aa
Y
==-
=-
cos.β 2
1
2
1
Тогда
21 12
2222
=+-+ ⇒=() ;aa
ZZ
a
Z
=± 2;
a =
±{, }.,11 2
Задачи для самостоятельного решения
14) Зная проекции нескольких векторов на ось l: пр
l
a
= 5;
пр
l
b
= -3; пр
l
c
= -8; пр
l
d
= 6, можно ли заключить, что они образу-
ют замкнутую ломаную линию?
15) Зная, что
a
= 6; пр
l
a
= -3, найти угол между вектором
a
и
осью l.
16) Точка В(-1; 3; -4) является концом вектора
a
= {2; 4; -1}.
Определить координаты начала А.
17) Зная одну из вершин АВС — т. А(2; -5; 3) и векторы, совпа-
дающие с двумя его сторонами, —
AB
= {4; 1; 2};
BC
= {3; -2; 5},
найти остальные вершины и сторону
CA
.
18) В точке А(2; 1; -1) приложена сила
R
= 7. Зная две коорди-
наты этой силы Х = 2; Y = -3, определить направление и конец
вектора, изображающего силу.
19) Даны три последовательные вершины параллелограмма
А(1; -2; 3), В(3; 2; 1), С(6; 4; 4). Найти его четвертую вершину D.
20) Даны векторы
a
= {1; -2; 3};
b
= {0; 1; 2};
c
= {3; 0; -1}. Найти длину и направляющие ко-
синусы вектора
da bc=- -2 .
21) Определить координаты точки М, если ее
радиус-вектор составляет с координатными ося-
ми одинаковые углы и его модуль равен 3.
22) Стержни АС и ВС соединены между собой
и с вертикальной стеной при помощи шарниров
(рис. 2.5). На шарнирный болт С действует вер-
тикальная сила
F
,
F
= 1000 Н. Определить реак-
ции этих стержней на шарнирный болт, если
α = 30°; β = 60°.
23) Груз весом P подвешен на двух гибких
нитях АВ и АС, причем нить АС горизонтальна,
АВ составляет с вертикалью угол ϕ (рис. 2.6).
Найти силы натяжения нитей АВ и АС.
Рис. 2.5
Рис. 2.6

26
Задачи к разд. 2.5
Задача 1. Пусть
a
= 1;
b
= 3;
(, ).
ab =
π
3
Найти скалярное произ-
ведение
()().423
ab ab-⋅ +
Решение: Пользуясь свойствами 1
0
–3
0
, раскрываем скобки по
правилу умножения многочленов, затем используем определение
скалярного произведения и свойство 4
0
:
()()
c
42382123
810
22
2
ab ab aababb
aab
-⋅ +=-⋅+⋅-=
=+⋅
oos(, )
cos.
ab b-=
=⋅+⋅⋅-⋅=+- =-
3
81 10 13
3
39 815274
2
π
Задача 2. Пусть
a
= {4; -2; 3};
b
= {1; -2; 0};
c
= {2; 1; -3}. Найти
()().
ababc+⋅-+3
Решение: Находим координаты векторов
ma b=+3 ,
nabc=-+ :
m
= {4 + 3 ⋅ 1; -2 + 3 ⋅ (-2); 3 + 3 ⋅ 0} = {7; -8; 3};
n
= {4 - 1 + 2; -2 +
+ 2 + 1; 3 - 0 - 3} = {5; 1; 0} ⇒
m
⋅
n
= 7 ⋅ 5 + (-8) ⋅ 1 + 3 ⋅ 0 = 35 - 8 =
= 27.
Задача 3. Дано:
a
= {-1; 2; 3};
b
= {0; 1; -2};
c
= {2; 1; -3}. Найти
угол ϕ между векторами
a
и
dbc=-2 .
Решение:
d
= {2 ⋅ 0 - 2; 2 ⋅ 1 - 1; 2 ⋅ (-2) - (-3)} = {-2; 1; -1},
cos
()() ()
,ϕ=
⋅
=
--+⋅+⋅-
++ ++
==
ad
ad
12 21 31
1494 11
1
14 6
1
221
ϕ=arccos.
1
221
Задача 4. Найти проекцию
пр
CD
AB
,
если А(-1; 2; 3); В(0; 1; 2);
С(1; -2; 3); D(3; 1; 0).
Решение: Найдем
AB
= {1; -1; -1};
CD
= {2; 3; -3}, тогда
пр
CD
AB
AB CD
CD
=
⋅
=
⋅+-⋅+- -
++
12 13 13
49
() ()()
99
2
22
22
11
==.
Задачи для самостоятельного решения
24) Известно, что
a
= 3;
b
= 4;
(, ).
ab =
2
3
π
Найти:
а)
()();32 2
abab-+

27
б)
().
ab+
2
25) Известно, что
abc=== 1,
abc++= 0.
Найти
ab bc ca⋅+⋅+⋅ .
26) Известно, что
a = 3,
b = 2,
(, ).
ab =
π
3
Найти
ab- 2 .
27) Дано:
a = 2,
b = 5,
(, ).
ab =
2
3
π
Найти α, при котором век-
тор
pa b=+α 17
перпендикулярен вектору
qab=-3 .
28) Дано:
amn=-2 ,
mn==1,
(,).
mn =°120
Найти соsϕ, где
ϕ=(, ).
am
29) Доказать, что угол между диагоналями прямоугольника,
построенного на векторах
a,
ba b(),⊥
определяется формулой
cos.ϕ=±
-
+
ab
ab
22
22
30) Какому условию должны удовлетворять векторы
a,
b,
чтобы
вектор
ab+
был перпендикулярен
ab-
?
31) К вершине правильного тетраэдра с ребром a приложены
три силы, направленные вдоль его ребер. Определить величину
равнодействующей.
32) Даны векторы
a
= {5; 0; 4};
b
= {0; -1; 2};
c
= {3; 1; 4}. Найти
()().
acba+-2
33) Даны точки А(-1; 3; -7); В(2; -1; 5); С(0; 1; -5).Вычислить
()().22AB CB BC BA
-+
34) Вычислить, какую работу производит сила
F
= {6; -2; 1},
когда ее точка приложения, двигаясь прямолинейно, перемещает-
ся из положения А(3; 4; -2) в В(4; -2; -3).
35) Даны три силы
P
= {3; -4; 2};
Q
= {2; 3; -5};
R
= {-3; -2; 4},
приложенные к одной точке. Вычислить, какую работу производит
равнодействующая этих сил, когда ее точка приложения переме-
щается, двигаясь прямолинейно, из положения М
1
(5; 3; -7) в по-
ложение М
2
(4; -1; -4).
36) Даны вершины треугольника А(-1; -2; 4); В(-4; -2; 0);
С(3; -2; 1). Найти внутренний угол при вершине В.
37) Даны вершины треугольника А(3; 2; -3); В(5; 1; -1);
С(1; -2; 1). Определить внешний угол при вершине А.

28
38) Даны векторы
a
= {2; -3; 4};
b
= {4; 0; 5};
c
= {3; 1; 1}. Найти
пр
d
c,
если
dab=-2 .
39) Даны точки М(-5; 7; -6), N(7; -9; 9). Вычислить проекцию
вектора
a
= {1; -3; 1} на ось вектора
MN
.
40) Определить, при каком значении α перпендикулярны век-
торы
cab=+2
и
d,
если
ai jk=+-α 2 ;
bijk=++3 ;
di k=-3 .
41) Найти вектор
x,
коллинеарный вектору
a
= {2; 1; -1} и удо-
влетворяющий условию
xa⋅=3.
42) Сила
R
= {1; -8; -7} разложена по трем направлениям, одно
из которых задано вектором
ai jk=++22 .
Найти составляющую
F
силы
R
в направлении
a
.
Задачи к разд. 2.6
Задача 1. Известно, что
ab⊥ ,
a = 3,
b = 4.
Найти
()().32
ab ab-×-
Решение: Пользуясь свойствами 1
0
–3
0
, раскрываем скобки в
векторном произведении:
()() .323625
ab ab aabaabbbab-×-=×-×- ×+ ×=-×
По свойству 5
0
векторные произведения
aa×=0,
bb×=0.
Да-
лее по определению векторного произведения
()() sin( ,) .3255 53460
ab ab ab ab ab-×-=-×==⋅⋅ =
Задача 2. Даны векторы
ai jk=- +2 ,
bi j=+34.
Найти
()().23
ab ab-×+
Решение: Найдем координаты векторов
2
ab-
= {2 ⋅ 1 - 3;
-2 ⋅ 2 - 4; 2 ⋅ 1} = {-1; -8; 2},
ab+ 3
= {1 + 3 ⋅ 3; -2 + 4 ⋅ 3; 1} =
= {10; 10; 1}. Тогда
()()23182
10 10 1
82
10 1
12
10 1
1
ab ab
ijk
ijk
-×+=-- =
=
-
-
-
+
-
--
=- ++
8
10 10
28 21 70
ijk.
Задача 3. Дано: А(1; 2; 0), В(3; 0; -3), С(5; 2; 6). Найти площадь
треугольника АВС.

29
Решение: Находим координаты векторов
AB
= {2; -2; -3},
AC
=
= {4; 0; 6}. По свойству 4
0
SABAC
ABC
=×
1
2
.
Так как
AB AC
ijk
ijk
×=--=- -+223
40 6
12 24 8 ,
то
S
ABC
=++=
1
2
12 24 814
222
().кв. ед.
Задачи для самостоятельного решения
43) Даны:
a = 2,
b = 3,
(, ).
ab =
2
3
π
Найти
[( )( )] .32 3
2
ab ab+×-
44) Даны:
a = 10,
b = 2,
ab⋅=12.
Вычислить
ab× .
45) Векторы
a
и
b
составляют угол 45°. Найти площадь тре-
угольника, построенного на векторах
ab- 2
и
32
ab+ ,
если
a
=
=
b
= 5.
46) При каком значении коэффициента α векторы
pab=+α 5
и
qab=-3
окажутся коллинеарными, если
a
и
b
не коллинеар-
ны.
47) Найти координаты векторного произведения
()
abc++ ×
×-(),
ab2
если
aij=+2 ;
bi jk=- +3 ;
cj k=+2 .
48) Вычислить площадь параллелограмма, построенного на
векторах
a
= {0; -1; 1};
b
= {1; 1; 1}.
49) Даны точки А(2; -1; 2); В(1; 2; -1); С(3; 2; 1). Найти коорди-
наты векторного произведения
().BC CA CB
-×2
50) Найти площадь и высоту ВD треугольника АВС с вершина-
ми А(1; -2; 8); В(0; 0; 4); С(6; 2; 0).
51) Сила
F
= {2; -4; 5} приложена к точке А(4; -2; 3). Определить
момент этой силы относительно точки С(3; 2; -1).
52) Даны три силы
F
1
= {2; -1; -3};
F
2
= {3; 2; -1};
F
3
= {-4; 1; 3},
приложенные к точке A(-1; 4; -2). Найти величину и направля-
ющие косинусы момента равнодействующей этих сил относитель-
но точки В(2; 3; -1).
53) Найти координаты вектора
x,
перпендикулярного к векто-
рам
a
= {2; -3; 1};
b
= {1; -2; 3} и удовлетворяющего условию
xi jk⋅+ -=().27 10
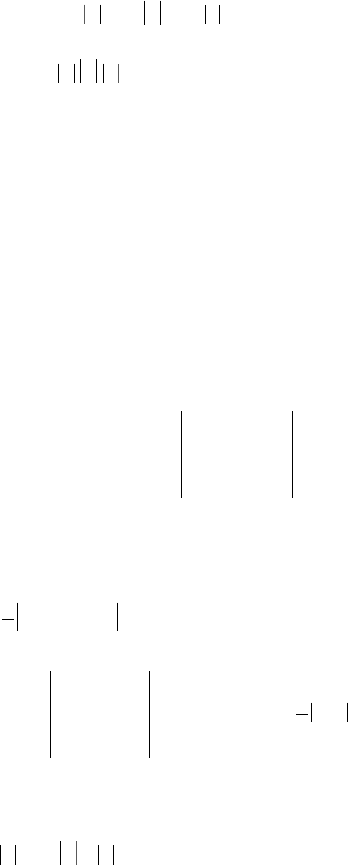
30
Задачи к разд. 2.7
Задача 1. Векторы
abc,,,
образующие правую тройку, взаимно
перпендикулярны,
a
= 2,
b
= 3,
c
= 4. Найти
abc.
Решение: Так как для правой тройки
abc
= V
пар
, построенного
на
abc,,,
а V
пар
=
abc
вследствие взаимной перпендикулярности
векторов, то
abc
= 24.
Задача 2. Показать, что
()() .
abacbabc++=-
Решение:
()()()()
abacbaba bcb
aab acbba
++=+ ×+×=
=++ bbbcb acbabc+==-
,
учитывая свойства 2
0
, 5
0
.
Задача 3. Даны векторы
a
= {1; -1; 3},
b
= {-2; 2; 1},
c
= {3; 0; -1}.
Вычислить
()()().2
bcabca b+++-
Решение: Находим координаты векторов 2
b
+
c
= {-4; 4; 2} +
+ {3; 0; -1} = {-1; 4; 1},
a
+
b
+
c
= {2; 1; 3},
a
-
b
= {3; -3; 2}, тогда
()()() .2
141
213
332
0
bcabca b+++-=
-
-
=
Задача 4. Вычислить объем треугольной пирамиды АВСD, если
А(2; -1; 1), В(5; 5; 4), С(3; 2; -1), D(4; 1; 3).
Решение: По свойству 4
0
имеем
VABACADABAC
∆пир
===-
1
6
363132
,{;;}, {; ;}. AAD
= {; ;},222
тогда
AB AC AD V
=-=- =- =
36 3
13 2
22 2
18
1
6
18 3.().
∆пир
куб.ед.
Задачи для самостоятельного решения
54) Вектор
c
перпендикулярен к векторам
a,
b,
угол между
a,
b
равен 30°,
a
= 6,
b
=
c
= 3. Вычислить
abc.
55) Показать, что
()()();
ababca bc abc---+-=23
