Жлуктенко В. І., Наконечний С. І. Теорія ймовірностей і математична статистика: У 2 ч. - Ч. І. Теорія ймовірностей
Подождите немного. Документ загружается.


178
то додатному приросту аргументу х +∆х відповідатиме від’ємний
приріст функції y – ∆y i похідна
0)(
<
Ψ
′
Y
.
А оскільки f (y)
≥
0, то об’єднуючи обидва випадки, дістанемо
(
)
(
)
(
)
YYfyf Ψ
′
Ψ= )(
(196)
Б. Загальна методика знаходження f (у).
Нехай неперервна випадкова величина Х задана щільністю ймо-
вірностей f (х), якщо
];[ bax
∈
.
Необхідно визначити f (у), якщо
(
)
xY
α
=
, де
(
)
x
α
є монотонною
функцією.
1. Необхідно визначити множину можливих значень для Y
Оскільки
,bxa ≤≤
то
(
)
)(bYa
α
≤
≤
α
.
2. Із
)(xY α=
знаходимо явний вираз Х через Y, а саме:
)(YX Ψ=
.
3. Знаходимо похідну
)( yХ
y
Ψ
′
=
′
.
4. Будуємо щільність імовірностей для випадковой величини Y
()
(
)
(
)
(
)
[
]
)();(, baYyyfyf αα∈Ψ
′
Ψ=
.
5. Перевіряється виконання умови нормування для f (у):
∫
α
α
=ω
)(
)(
1)(
b
a
yyf .
Якщо нормування виконується, то f (у) знайдено вірно.
За знайденою f (у) функцією розподілу ймовірностей визначається
()
∫
α
=
y
a
dyyfyF
)(
)( . (197)
Числові характеристики функцій неперервного випадкового ар-
гументу визначаються за формулами:
математичне сподівання
()
dxxfxdyyyfYM
b
a
b
a
∫∫
α
α
α==
)(
)(
)()()(
; (198)
дисперсія
()
(
)
() () ()
()
(
)
∫
α
α
=−=−=
b
a
YMdyyfyYMYMYD
2222
()() ()
∫
−α=
b
a
YMdxxfx
22
; (199)
середнє квадратичне відхилення
(
)
(
)
YDY =σ . (200)
179
Приклад 3.
Задано
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<
≤
=
.1,0
,10,
7
10
,0,0
7
3
x
xx
x
xf
Знайти f (у), F (у), якщо Y = 2x
2
.
Обчислити М (Y); D (Y);
σ
(Y).
Розв’язання. Використовуючи загальну методику знаходження f (у),
дістанемо наведені далі висновки.
1. Знаходимо інтервал можливих значень для випадкової величини Y:
10
≤
≤
X
;
20
≤
≤
Y
,
оскільки на проміжку
[]
2
21,0 xY =
є монотонно зростаючою функцією.
2. Із функціональної залежності Y = 2х
2
записуємо явний вираз
)(
2
y
y
X Ψ==
.
3. Знаходимо похідну функції
)( y
Ψ
.
24
1
)(
2
1
−
⎟
⎠
⎞
⎜
⎝
⎛
=Ψ
′
y
y
4. Використовуючи (196), будуємо функцію f (у):
() ( )( )
7
2
14
4
2
1
14
3
214
5
214
15
24
1
27
10
)()(
−−−
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
=Ψ
′
Ψ=
yyyy
yyfyf
.
5. Перевіряємо виконання умови нормування:
()
.1
25
7
2
2
14
5
214
5
214
5
1
2
0
7
5
2
0
7
5
7
2
2
0
7
2
2
0
2
0
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
→=
−−
∫∫∫
yy
dy
y
dy
y
dyyf
Нормування виконується, тому щільність імовірностей випадкової
величини Y
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<
≤
=
−
.2,0
;20,)
2
(
14
15
;0,0
7
2
y
y
y
y
yf
180
Використовуючи (197), знаходимо
()
.
22214
5
)(
7
5
0
7
5
7
2
00
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
==
−
∫∫
yy
dy
y
dyyfyF
y
yy
Отже,
()
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
>
≤<
⎟
⎠
⎞
⎜
⎝
⎛
≤
=
.2,1
;20,
2
;0,0
7
5
y
y
y
y
yF
Використовуючи формули (198), (199), (200), знаходимо числові ха-
рактеристики:
()
.
6
5
24
20
22
24
5
7
12
4
14
5
4
14
5
214
5
)(
7
12
7
2
2
0
7
12
7
7
5
2
0
7
7
2
2
0
2
0
==⋅=
===
⎟
⎠
⎞
⎜
⎝
⎛
==
∫∫∫
−
y
dyydy
y
ydyyyfYM
М(Y) можна обчислити, не відшукуючи f (у):
.
6
5
25
20
7
24
7
20
7
20
7
10
2)(
1
0
7
24
1
0
7
17
7
3
1
0
2
=====
∫∫
x
dxxdxxxYМ
6
5
)( =YM
.
;
19
20
38
40
8
38
5
22
38
5
7
19
4
14
5
4
14
5
214
5
)()(
7
19
7
2
2
0
7
19
7
2
0
7
12
7
7
2
2
0
2
2
0
22
===⋅==
==
⎟
⎠
⎞
⎜
⎝
⎛
==
∫∫∫
−
y
dyydy
y
ydyyfyYM
()
()
()
;
684
245
684
475720
26
25
19
20
6
5
19
20
2
22
=
−
=−=
⎟
⎠
⎞
⎜
⎝
⎛
−=−= YMYMYD
181
Так само, як і для М (Y):
()
19
20
38
40
7
38
7
40
7
40
7
40
7
10
)2(
1
0
7
38
1
0
7
31
7
3
1
0
4
7
3
1
0
222
======
∫∫∫
x
dxxdxxxdxxxYM
.
()
.
684
245
36
25
19
20
=−=YD
()
.
19
245
6
1
684
245
)( ===σ YDY
В. Функція
()
xα
немонотонна.
Нехай
()
xY α=
, де функція
(
)
x
α
є немонотонною функцією, зо-
браженою на рис. 73.
y
y + y
∆
x
xx
11 1
+
∆
xx x
kk k
+
∆
0
x
Рис. 73
У цьому разі обернена функція до
(
)
(
)
yXx
Ψ
=
α
буде неодно-
значною, а саме Y = у буде відповідати в загальному випадку мно-
жина обернених функцій
)(...,),(),(
21
yyy
k
ψ
ψ
ψ
.
І, очевидно, що випадковій події
yyYy
∆
+
<
<
відповідатимуть k
несумісних випадкових подій:
)(...,,)(),(
222111 kkk
xxXxxxXxxxXx
∆
+
<
<
∆
+
<
<
∆+<
<
.
Отже, у цьому разі
()( )
∑
=
∆+<<=∆+<<
k
i
iii
xxХxPyyYyP
1
або, використовуючи влас-
тивості функції розподілу ймовірностей, можна записати:
()
∑
=
−∆+=−∆+
k
i
iii
xFxxFyFyyF
1
)()()()(
.
182
Тоді
()
=
∆
−∆+
=
∆
−∆+
=
′
=
∑
=
→∆→∆
k
i
iii
yy
y
xFxxF
y
yFyyF
yFyf
1
00
)()()()(
)(
limlim
=
∆
∆
∆
−∆+
=
=
∆
∆
∆
−∆+
=
→∆
=
→∆
=
→∆→∆
∑
∑
y
x
x
xFxxF
y
x
x
xFxxF
i
y
i
iii
k
i
x
i
k
i
i
iii
xy
i
i
limlim
lim
0
1
0
1
0,0
)()(
)()(
=
()
.)()())((
11
yyfxxf
i
k
i
iy
k
i
i
Ψ
′
Ψ=
′
∑∑
==
Отже,
() ( )
.)()(
1
yyfyf
i
k
i
i
Ψ
′
Ψ=
∑
=
(201)
Методика знаходження f (у) така сама, як і для монотонної функ-
ції. Щоб обчислити числові характеристики, можна використати
формули (198), (199), (200).
Приклад 4. Задано
()
.,
2
1
2
2
∞<<∞−
π
=
−
xexf
x
Знайти f (у), якщо Y = x
2
.
Розв’язання. Побудуємо графіки f (х), Y = x
2
(pис. 74 і 75).
f
x
()
0
x
0
x
Y = x
2
y
Рис. 74 Рис. 75
1. Якщо
∞<<∞− Х
, то
∞
<
<
Y0 .
2. Оскільки Y = х
2
є немонотонною функцією при ∞
<
<
∞
Х
, знахо-
димо обернені функції:
,)(
11
Yyx =Ψ= Yyx −=Ψ= )(
22
.

183
3. Похідні від обернених функцій будуть:
,
2
1
)(
11
y
yx =Ψ
′
=
′
y
yx
2
1
)(
22
−=Ψ
′
=
′
.
4. Будуємо функцію f (у), використовуючи (201):
() ()()()()()()
=Ψ
′
Ψ+Ψ
′
Ψ=Ψ
′
Ψ=
∑
=
)()()()()()(
2211
2
1
yyfyyfyyfyf
i
i
i
22
1
22
2
1
2
1
2
1
2
1
2
1
yyy
ey
y
e
y
e
−−−−
π
=
π
+
π
=
.
5. Перевіряємо виконання умови нормування:
.1
2
2
2
2
2
2
2
2
1
1)(
0
2
2
2
22
1
00
=
π
π
=
=Ζ
Ζ
π
=
=
=
=
π
→=
∫∫∫
∞
Ζ
−
−−
∞∞
d
ez
zdzdy
zy
dyeydyyf
y
Отже, умова нормування виконується, a це свідчить про те, що f (у)
знайдено правильно.
Остаточно записуємо:
()
⎪
⎩
⎪
⎨
⎧
>
π
≤
=
−−
.0,
2
1
;0,0
22
1
yey
y
yf
y
Відшукаємо числові характеристики:
() ()
.1
2
2
0
2
2
2
2
,
2
2
2
2
1
2
1
0
2
0
2
22
2
0
22
2
0
2
1
22
1
0
22
22
2
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
π
+
π
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+−
π
=
=
=→=
==
=
π
==→==
=
π
=
π
==
∫
∫
∫∫
∞
−
∞
−
−−
−
∞
−
∞
−−
∞
dzeze
evdvdzze
dzduzu
dzezzdzdyzy
dyeydyeyydyyyfYM
zz
zz
z
yy
M (Y) = 1.
Для обчисленя дисперсії D (Y) знаходимо
184
()
.
2
4
2
2
2
2
2
2
,
2,
2
2
2
2
1
2
1
)(
0
2
0
2
2
2
0
0
2
2
22
2
2
2
0
32
2
0
2
3
2
1
2
1
00
222
2222
22
π
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−−
π
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+−
π
=
=
−==
==
=
π
==→==
=
π
=
π
==
∞
−
∞
−−
∞
∞
−
−−
−
∞
−
∞
−−
∞∞
∫
∫
∫∫∫
zzzz
zz
z
y
eezdzezez
evdvdzze
zdzduzu
dzezzdzdyzy
dyeydyeyydyyfyYM
()
π
=
2
4
YM
.
()
()
π
π−
=−
π
=−=
2
24
1
2
4
)(
22
YМYMYD
.
4. Функції двох випадкових аргументів
та їх числові характеристики
У загальному випадку функцію двох аргументів Х і Y можна поз-
начити як
(
)
yxZ ,
α
=
, (202)
де α є невипадковою функцією.
Якщо Х та Y є дискретними випадковими величинами, то і Z буде
дискретною. Якщо Х та Y є неперервними, то і Z буде неперервною.
4.1. Знаходження F (z), f (z), якщо Z = Х + Y
Розглянемо функціональну залежність Z = Х + Y, де Х і Y є непе-
рервними випадковими величинами.
Потрібно за
відомою щільністю f (x, y) знайти F (z), f (z).
Імовірність влучення Z в області Z < z, а саме Z < Х + Y зобра-
жено на рис. 76.
0
x
y
Z < X + Y
Рис. 76
185
Ця ймовірність обчислюється так:
()()()
∫∫
∞
∞−
−
∞−
==<=<+
xz
dxdyyxfzFzZPZYXP ),(
(203)
або
()()()
∫∫
∞
∞−
−
∞−
==<=<+ .),(
yz
dxdyyxfzFzZPZYXP
(204)
Оскільки
∫∫∫∫
−
∞−
∞
∞−
∞
∞−
−
∞−
=
xzxz
dxdyyxfdxdyyxf ),(),(
,
∫∫∫∫
−
∞−
∞
∞−
∞
∞−
−
∞−
=
yzyz
dxdyyxfdxdyyxf ),(),(
,
то формули (203), (204) можна подати так:
()
;),(
∫∫
−
∞−
∞
∞−
=
xz
dxdyyxfzF
(205)
()
.),(
∫∫
−
∞−
∞
∞−
=
yz
dxdyyxfzF
(206)
Тоді щільність імовірностей для випадкової величини Z буде така:
() ()
;),(),(
∫∫∫
∞
∞−
−
∞−
∞
∞−
−=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
′
= dxxzxfdydxyxfzFzf
z
xz
() ()
∫∫∫
∞
∞−
−
∞−
∞
∞−
−=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
′
= .),(),( dyyyzfdxdyyxfzFzf
z
yz
Отже,
()
;),(
∫
∞
∞−
−= dxxzxfzf
(207)
()
∫
∞
∞−
−= .),( dyyyzfzf
(208)
Якщо випадкові величини Х і Y є незалежними, то f (x, y) =
= f (x) f (y). За цієї умови формули наберуть такого вигляду:
()
;)()(
∫
∞
∞−
−= dxxzfxfzf
(209)
()
.)()( dyyfyzfzf
∫
∞
∞−
−=
(210)
Формули (209), (210) називають згорткою, або композицією,
двох законів.
186
Приклад 5. Задано закони розподілу ймовірностей незале-
жних випадкових величин Х, Y:
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−
−≤
=
.2,0
;24,
6
1
;4,0
x
x
x
xf
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−
−≤
=
.6,0
;62,
8
1
;2,0
y
y
y
yf
Знайти F (z), f (z), якщо Z = X + Y. Побудувати графіки
F (z), f (z).
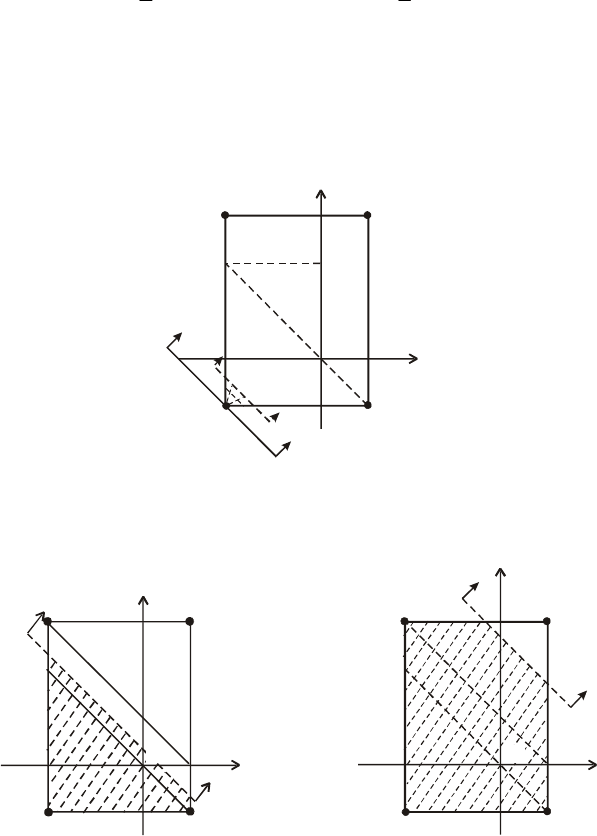
Розв’язання. Побудуємо множину
Ω
-сумісної появи випадкових
величин Х і Y. Ця множина зображена на pис. 77.
(– 4; 6)
(– 4; – 2)
(2; – 2)
(2; 6)
(– 4; 0)
у
6
– 2
– 4 0 2
х
Рис. 77
Пряма Z = Х + Y зі збільшенням Z рухатиметься паралельно сама
собі, відтинаючи від множини
Ω
змінні площі (pис. 77, 78 і 79).
(– 4; 6)
(– 4; – 2)
(2; – 2)
(– 4; 0)
– 2
– 4
2
(2;6)
х
0
6
у
(– 4; 6) (2; 6)
(– 4; –2) (2; – 2)
у
6
s
–
2
х
0 2
– 4
Pис. 78 Рис. 79
187
У точці (– 4; –2) Z = – 6; у точці (2; –2) Z = 0; у точці (– 4; 6)
Z = 2; у точці (2; 6) Z = 8.
1. При Z < – 6 F (z) = 0.
2. У разі зміни Z у проміжку – 6 < Z < 0 маємо:
()
()
()()
.
96
6
2
2
48
1
2
48
1
48
1
48
1
48
1
8
1
6
1
)()(
2
2
4
2
2
4
2
42
2
42
2
42
2
42
2
42
1
+
=
−+
−=
=−+=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
=
====
+
−
+
−
+
−
−
−
+
−
−
−
+
−
−
−
+
−
−
−
+
−
−
−
∫∫∫∫
∫∫∫∫∫∫
zxz
dxxzdxydxdy
dxdydxdydydxyfxfzF
z
zzxzzxz
zxzzxzzxz
Отже, на проміжку [– 6; 0] функція розподілу ймовірностей зміню-
ється за законом
()
(
)
.
96
6
2
+
=
z
zF
3. Оскільки в точці (– 4; 4) Z = 0, то на проміжку [0; 2] маємо:
()
()
.
8
3
96
1236
6
4896
36
4896
36
48
1
96
36
48
1
96
36
48
1
0)(
2
4
2
4
2
4
2
4
12
+
=
+
=
=+=+=+−+=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+=
⎟
⎠
⎞
⎜
⎝
⎛
+=
∫∫
∫∫∫
−−
−
−
−−
−
−
zz
z
dx
z
dxxxz
dxydxdyFZF
xz
x
xz
x
Отже, на проміжку [0, 2], що зображено на рис. 78, функція розподі-
лу ймовірностей змінюється за законом
.
8
3
)(
2
+
=
z
zF
4. У точці (2, 6) Z = 8 і функція розподілу ймовірностей при своїй
зміні наближатиметься до одиниці. Щоб дістати аналітичний вираз для
F(z), від одиниці віднімаємо змінну площу S трикутника, зображеного
на рис. 79.
()
()
() ()
.
96
8
1
2
6
48
1
16
48
1
1
48
1
1
48
1
1
48
1
1
2
2
6
2
2
6
2
6
6
2
6
62
6
6
3
zxz
dxxz
dxydxdydxdyZF
zz
zxzzxzzxz
−
−=
+−
−=+−−=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
⎟
⎠
⎞
⎜
⎝
⎛
−=−=
−−
−−−−−−
∫
∫∫∫∫∫
