Жлуктенко В. І., Наконечний С. І. Теорія ймовірностей і математична статистика: У 2 ч. - Ч. І. Теорія ймовірностей
Подождите немного. Документ загружается.

168
15. Задано
Ω
∈
= ),(,),( YXayxf якщо
;
Ω∈= ),(,0),( YXyxf якщо
,
де
).0,10(
2
xyx ≤≤≤≤=Ω
Знайти а і r
xy
.
Відповідь. а = 3; r
xy
= 0.
16. Задано
Ω∈+= ),(),(),(
2
YXxxyayxf якщо
;
Ω∈= ),(,0),( YXyxf якщо ,
де
).,10(
2
xyxx ≤≤≤≤=Ω
Знайти а і побудувати кореляційну матрицю.
Відповідь.
11
120
=a
;
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
0423,0035,0
035,081,0
K
.
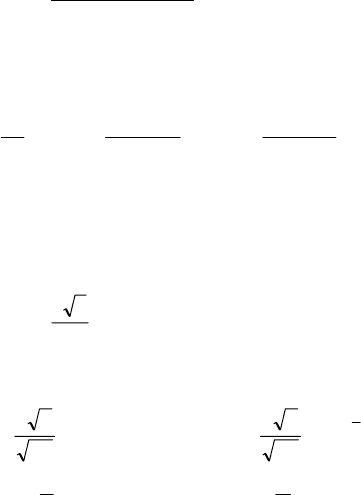
17. Закон системи двох дискретних випадкових величин (Х, Y)
задано таблицею:
Х
Y
2,2 4,2 6,2 1,2
i
y
p
2,5 0,02 а 0,08 0,1
3,5 а 0,04 0,06 0,2
4,5 0,08 0,06 0,6а 0,1
j
x
p
Знайти ймовірності
331221
;; ppp ; побудувати кореляційну матри-
цю і нормовану кореляційну матрицю.
Відповідь:
06,0;1,0;1,0
331221
=
=
= ppp .
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
=
6,013,0
13,0432,5
K
;
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
1072,0
072,01
.
18. Задано
Ω
∈
+= ),(,)1(),( YXxxyayxf якщо
;
Ω∈= ),(,0),( YXyxf якщо ,
де
{
}
xyxx ≤≤≤≤=Ω ,10 .
Знайти а і побудувати кореляційну матрицю і нормовану кореля-
ційну матрицю.
Відповідь.
23
105
=a
;
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
2995,014,0
14,009478,0
K
;
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
1827,0
827,01
.
169
19. Брак у продукції заводу внаслідок дефекту А становить 6%.
Водночас серед забракованої за дефектом А продукції 4% таких, що
мають дефект В, а в продукції, в якій відсутній дефект А, дефект В
зустрічається в 1% випадках.
Знайти коефіцієнт кореляції між дефектами А і В.
Відповідь. r
AB
= 0,0936.
20. За заданою кореляційною матрицею чотиривимірної випад-
кової величини
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−
=
25
4,09
5,07,04
8,012,01
K
знайти нормовану кореляційну матрицю.
Відповідь.
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
−
1
03,01
05,0117,01
16,0333,01,01
.
21. Задано
,
1
),(
2222
yxyx
a
yxf
+++
=
якщо (Х, Y)
∈ Ω де
{
}
∞
<
<
∞
−
∞
<
<
−
∞=Ω yx ; .
Знайти а і f(x), f(y). З’ясувати, чи існує кореляційний зв’язок між
випадковими величинами Х і Y.
Відповідь.
.
)1(
1
)(;
)1(
1
)(;
1
222
y
yf
x
xfa
+π
=
+π
=
π
=
Оскільки
)()(),( yfxfyxf = , то 0
=
XY
K .
22. Відомо, що
8,0)()(
=
=
BPAP . Яке значення повинна мати
)/( BAP
, щоб коефіцієнт кореляції між А і В дорівнював 0,6?
Відповідь.
92,0)/( =BAP .
23. Задано
22
964
33
),(
yxyx
eyxf
−−−
π
=
, – ∞ < х < ∞; – ∞ < у < ∞.
Знайти
)./(),/(),/(),/( xYMyXMxyfyxf
Відповідь.
.
3
)/(;
4
9
)/(
;
2
22
)/(;
2
26
)/(
2
2
)
2
9
2(
)3(
x
xYMyyXM
exyfeyxf
yx
yx
−=−=
π
=
π
=
+−
+−

170
24. Випадкові події А і В мають однакову ймовірність появи, яка
дорівнює р. Яка повинна бути умовна ймовірність Р(А/B), якщо ві-
домо, що коефіцієнт кореляції між випадковими подіями А і В дорі-
внює r.
Відповідь. Р(А/B) = р + r (1 – р).
25. Визначити кореляційну матрицю системи випадкових вели-
чин (
Х, Y), якщо щільність імовірностей
222
)1(
2
),(
++π
=
yx
yxf
.
Відповідь.
⎟
⎠
⎞
⎜
⎝
⎛
=
5,00
05,0
K
.
26. За заданою кореляційною матрицею системи випадкових ве-
личин
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−−
−
=
252010
203014
101449
K
побудувати нормовану кореляційну матрицю.
Відповідь.
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−
−
1
3
2
7
2
3
2
1
3
1
7
2
3
1
1
.
27. Відомі значення p (A) = 0,02, p (B) = 0,04, p (B / A) = 0,03.
Обчислити коефіцієнт кореляції між A i B.
Відповідь: r
AB
≈ 0,0072.
28. Двоє робітників виготовляють однотипні вироби. Імовірність
того, що виріб, виготовлений першим робітником, є стандартним,
дорівнює 0,9; для другого робітника ця ймовірність дорівнює 0,85.
Позначивши через X число стандартних виробів, виготовлених пер-
шим робітником, а через Y число стандартних виробів, виготовлених
другим робітником, побудувати функції розподілу F(x, y), системи
випадкових величин (X, Y
).
Відповідь:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤
≤
≤
=
.2,1
,2,18,0
,1,01,0
,0,0
)(
x
x
x
x
xF
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<
≤<
≤
=
.2,1
,21,225,0
,10,0225,0
,0,0
)(
y
y
y
y
yF
171
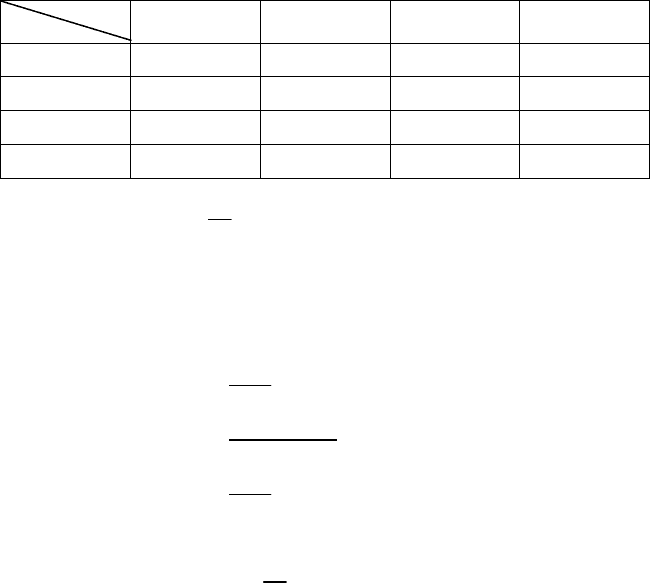
F (x, y) подано в табличній формі:
X
Y
x ≤ 0 0 < x ≤ 1 1 < x ≤ 2 x > 2
y ≤ 0 0 0 0 0
0 < y ≤ 1 0 0,000225 0,00405 0,01
1 < y ≤ 2 0 0,00405 0,0455 0,18
y > 2 0 0,0225 0,225 1
29. Задано
72
1
)( =xf
, якщо (x, y) ∈ Ω,
0)( =xf , якщо (x, y) ∉ Ω ,
де
Ω = {– 4 ≤ x ≤ 5, – 3 ≤ y ≤ 5}.
Знайти F (x, y) і обчислити P (–1 < x < 4, –2 < y < 3).
Відповідь.
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎨
⎧
>>
≤<−>
+
≤<−≤<−
++
>≤<−
+
−≤−≤
=
.5,5,1
;53,5,
8
3
;53,54,
72
)3)(4(
;5,54,
9
4
;3,4,0
),(
yx
yx
y
yx
yx
yx
x
yx
yxF
()
72
25
32,41 =<<−<<− yxP
.
30. Незалежні випадкові величини X i Y задані щільностями ймо-
вірностей:
⎩
⎨
⎧
>
≤
=
−
;0,3
;0,0
)(
3
xe
x
xf
x
⎩
⎨
⎧
>
≤
=
−
.0,5
;0,0
)(
5
ye
y
yf
y
Записати вирази для f
(x, y), F (x, y).
Відповідь:
⎩
⎨
⎧
>>
≤≤
=
+−
.0,0,15
;0,0,0
),(
)53(
yxe
yx
yxf
yx
⎩
⎨
⎧
>>
≤≤
=
−
.0,0,15
;0,0,0
),(
3
yxe
yx
yxF
x
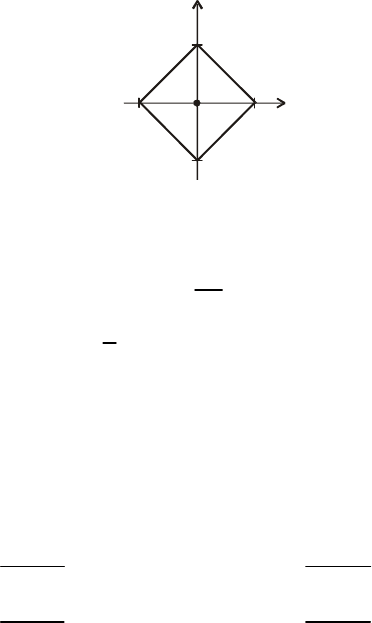
31. Система двох неперервних випадкових величин має сталу
щільність yсередині квадрата, зображеного на рис. 69.

172
–
2 0 2
х
у
2
–2
Ω
Рис. 69
Знайти вирази для )/(),/(,)(),(),,( xyfyxfyfxfyxf , M(X / y), M(Y / x).
Відповідь.
⎪
⎩
⎪
⎨
⎧
Ω∈
Ω∈
=
.),(,
2
1
;),(,0
),(
YX
YX
yxf
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
>
≤<
−
≤<−
+
−≤
=
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−
≤<−+
−≤
=
;2,0
;20,
)2(2
1
;02,
)2(2
1
;2,0
)/(
;2,0
;20),2(
;02),2(
;2,0
)(
x
x
x
x
x
x
yxf
x
xx
xx
x
xf
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
>
≤<
−
≤<−
+
−≤
=
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−
≤<−+
−≤
=
.2,0
;20,
)2(2
1
;02,
)2(2
1
;2,0
)/(
;2,0
;20),2(
;02),2(
;2,0
)(
y
y
y
y
y
y
xyf
y
yy
yy
y
yf
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
>
≤<
−
≤<−
+
−
−≤
=
;2,0
;20,
2
1
;02,
2
1
;2,0
)/(
x
x
x
x
x
x
yXM
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
>
≤<
−
≤<−
+
−
−≤
=
.2,0
;20,
2
1
;02,
2
1
;2,0
)/(
y
y
y
y
y
y
xYM
32. Система двох неперервних випадкових величин (Х, Y) має
сталу щільність імовірності всередині квадрата, зображеного на
рис. 70.
173
1
–1
–1 0 1
х
y
Рис. 70
Знайти вирази для
)./(),/(,)(),(),,( xyfyxfyfxfyxf
З’ясувати
залежність і корельованість між випадковими величинами Х і Y.
Відповідь.
⎪
⎩
⎪
⎨
⎧
Ω∈
Ω∈
=
.),(,
2
1
;),(,0
),(
YX
YX
yxf
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−
≤<−+
−<
=
;1,0
;10,1
;01,1
;1,0
)(
x
xx
xx
x
xf
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−
≤<−+
−≤
=
.1,0
;10,1
;01,1
;1,0
)(
y
yy
yy
y
yf
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
≤<
−
≤<−
+
−≤
=
;10,
)1(2
1
;01,
)1(2
1
;1,0
)/(
x
x
x
x
x
yxf
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
≤<
−
≤<−
+
−≤
=
.10,
)1(2
1
;01,
)1(2
1
;1,0
)/(
y
y
y
y
y
xyf
)()(),( yfxfyxf
≠
. Випадкові величини Х та Y не корельовані, але
залежні K
ХY
= 0.
ТЕМА 8. ФУНКЦІЇ ВИПАДКОВИХ АРГУМЕНТІВ
1. Функції одного випадкового аргументу
Функцією випадкового аргументу Х називають таку випадкову ве-
личину Y, яка набуває значення Y = у =
α
(х) щоразу, коли Х = х, де α є
невипадковою функцією. Якщо Х є дискретною випадковою величи-
ною, то і функція випадкового аргументу Y =
α
(х) буде дискретною.
Коли Х є неперервною випадковою величиною, то і Y =
α
(х) буде
неперервною.
174
1.1. Функції дискретного
випадкового аргументу
Нехай закон дискретної випадкової величини Х задано таблицею:
Х = х
i
x
1
x
2
x
3
............ x
k
P(X = x
i
) = p
i
p
1
p
2
p
3
............. p
k
Тоді закон розподілу випадкової величини Y =
α
(х) матиме та-
кий вигляд:
Y =
α
(х
i
)
α
(х
1
)
α
(х
2
)
α
(х
3
)
..................
α
(х
k
)
P(Y =
α
(х
i
) = р
i
p
1
p
2
p
3
............... p
k
де кожне можливе значення Y дістають, виконуючи ті операції, які
вказані в невипадковій функції, умовно позначеній
α
.
При цьому, якщо в законі розподілу випадкової величини Y є по-
вторення значень, то кожне з цих значень записують один раз, до-
даючи їх імовірності.
Приклад 1.
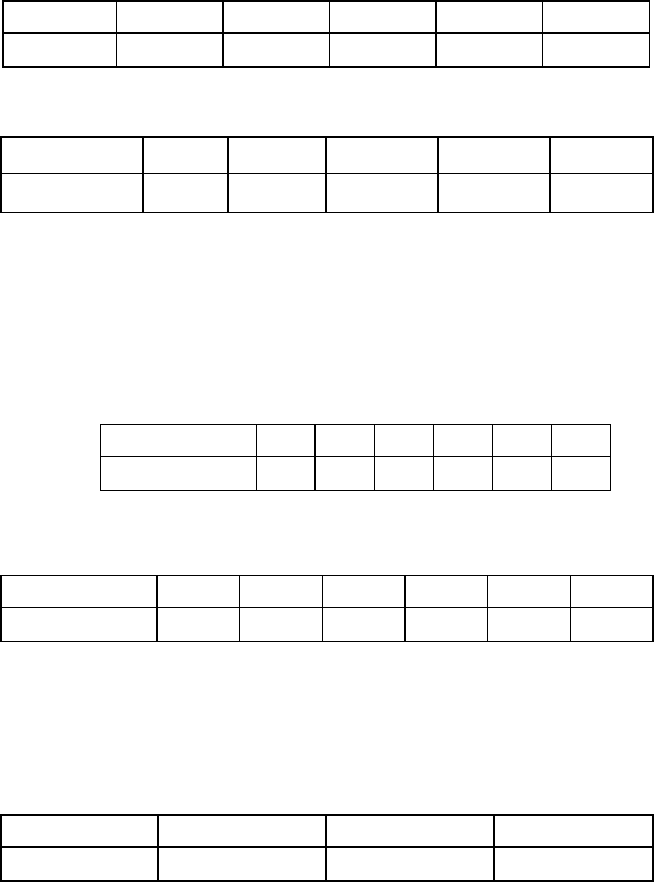
Закон розподілу дискретної випадкової величини Х задано
таблицею:
Х = х
i
– 4 –2 –1 1 2 4
Р(X = х
i
) = р
i
0,1 0,2 0,1 0,1 0,2 0,3
Побудувати закон розподілу ймовірностей для Y = 3х
2
.
Розв’язання. Iз функціональної залежності Y = 3х
2
маємо:
Y = 3х
i
2
16 4 1 1 4 16
Р(у = 3х
i
2
) = р
i
0,1 0,2 0,1 0,1 0,2 0,3
Ураховуючи повтори можливих значень Y, дістаємо:
Р (у = 16) = 0,1 + 0,3 = 0,4;
Р (у = 4) = 0,2 + 0,2 = 0,4;
Р (у = 1) = 0,1 + 0,1 = 0,2.
Отже, закон розподілу дискретної випадкової величини Y набирає
такого вигляду:
Y = у
j
1 4 16
Р (у = у
j
) = р
j
0,2 0,4 0,4
175
2. Числові характеристики функції
дискретного випадкового аргументу
1. Математичне сподівання
() ( )
∑∑
==
=ϕ=
m
j
jjii
k
i
pypxYM
11
.
(190)
2. Дисперсія
()
()
() ( ) () ()
YMpyYMpxYMYMYD
jj
m
j
ii
k
i
22
1
22
1
22
−=−ϕ=−=
∑∑
==
. (191)
3. Середнє квадратичне відхилення
(
)
(
)
.YDY =σ
(192)
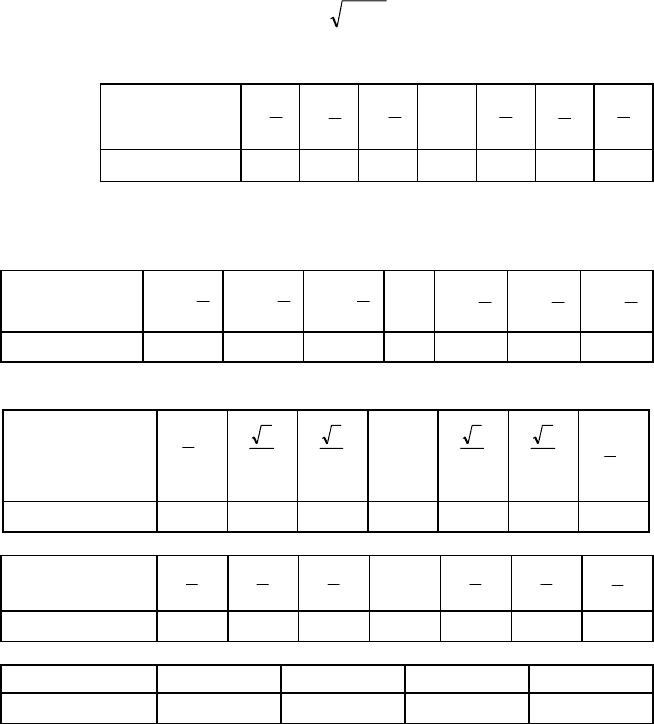
Приклад 2. За заданим законом розподілу
Х = х
i
3
π
−
4
π
−
6
π
−
0
6
π
4
π
3
π
Р (Х = х
i
) = p
i
0,1 0,2 0,1 0,1 0,2 0,1 0,2
Обчислити М (Y), D (Y), σ (Y), якщо Y = cos
2
х.
Розв’язання. Побудуємо закон розподілу Y.
Y = cos
2
хi
⎟
⎠
⎞
⎜
⎝
⎛
π
−
3
cos
2
⎟
⎠
⎞
⎜
⎝
⎛
π
−
4
cos
2
⎟
⎠
⎞
⎜
⎝
⎛
π
−
6
cos
2
0cos
2
6
cos
2
π
4
cos
2
π
3
cos
2
π
Р (Y = cos
2
х
i
) = p
i
0,1 0,2 0,1 0,1 0,2 0,1 0,2
або
Y
= cos
2
х
i
2
2
1
⎟
⎠
⎞
⎜
⎝
⎛
2
2
2
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
2
2
3
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
1
2
2
3
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
2
2
2
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
2
2
1
⎟
⎠
⎞
⎜
⎝
⎛
Р (Y = cos
2
х
i
) = p
i
0,1 0,2 0,1 0,1 0,2 0,1 0,2
Y
= cos
2
х
i
4
1
2
1
4
3
1
4
3
2
1
1
4
Р (Y = cos
2
х
i
) = p
i
0,1 0,2 0,1 0,1 0,2 0,1 0,2
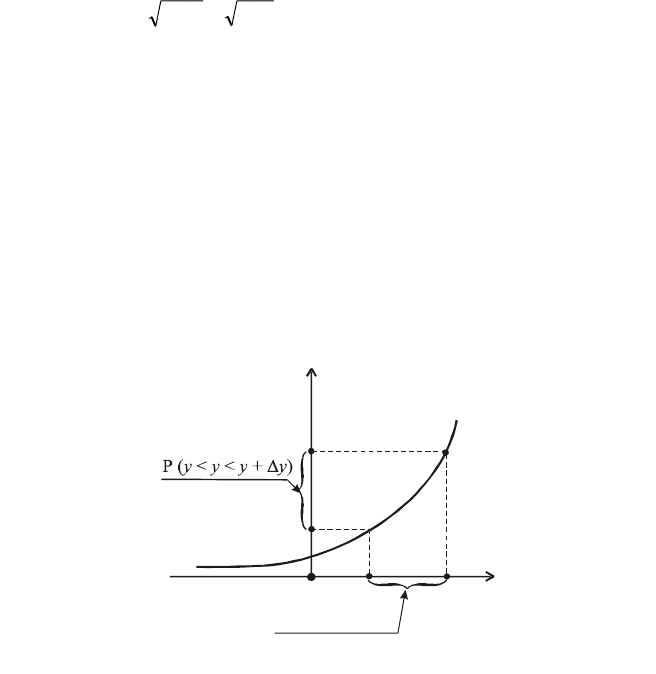
Y
=
у
j
0,25 0,5 0,75 1
Р (Y = у
j
) = p
j
0,3 0,3 0,3 0,1
176
()
()
()
()
()
()
()
() ()
()
.245,0
;245,006,0
;06,0
;06,03025,03625,0
;3625,01,016875,0075,001875,0
1,103,05625,03,025,03,00625,0
;55,055,01,0225,015,0075,0
1,013,075,03,05,03,025
,0р
22
4
1
2
2
4
1
=σ
≈==σ
=
=−=−=
=+++=
=+⋅+⋅+⋅==
=→=+++=
=⋅+⋅+⋅+⋅==
∑
∑
=
=
Y
YDY
YD
YMYMYD
pyYM
YM
yYM
j
ji
j
jj
3. Функції неперервного випадкового
аргументу та їх числові характеристики
Нехай закон розподілу ймовірностей неперервної випадкової ве-
личини Х задано щільністю f (х).
Необхідно знайти f (у), якщо Y =
)(x
α
.
А. Функція
)(xα
монотонна.
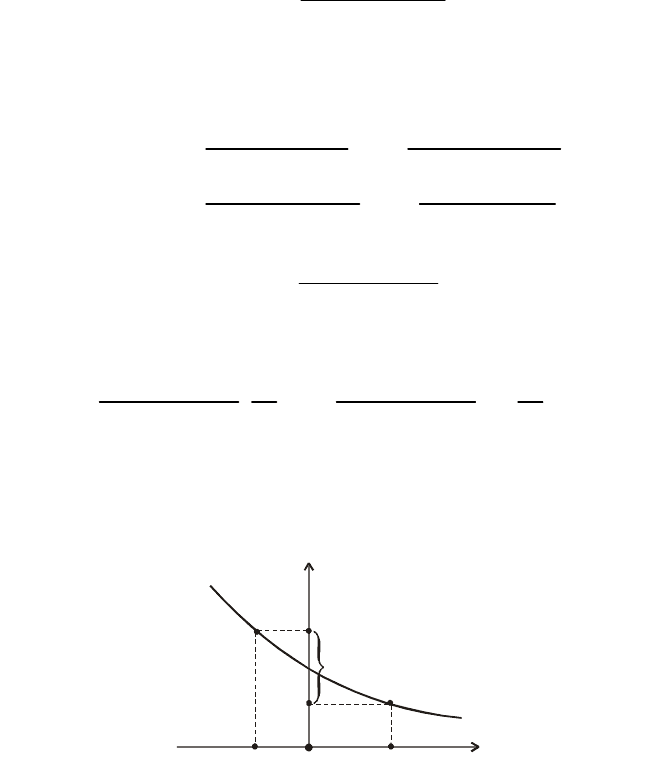
Розглянемо випадок, коли Y =
)(x
α
є монотонно зростаючою функ-
цією, зображеною на pис. 71.
уу
+
∆
у
0 +
ххх х
∆
Y
Y = x
α
()
P ( )
x < x < x + x
∆
Рис. 71
177
Якщо випадкова величина Х міститься у проміжку [х; х + ∆х], то
оскільки Y жорстко зв’язана з випадковою величиною Х функцією
α
(х), то Y міститиметься у проміжку [у, у + ∆у] (рис. 71). Отже, по-
дії х < Х < х +∆х і у < Y < у +∆у будуть рівноймовірними:
Р(х < Х < х +∆х) = Р(у < Y < у +∆у). (193)
Згідно з визначенням щільності ймовірностей
()
y
yFyyF
yf
y
∆
−∆+
=
→∆
)()(
lim
0
.
Але
F( у +
∆
у) – F(у) = Р (у < Y < у +∆у) = Р (х < Х < х +∆х) згідно зі
(193).
Тоді:
()
()()
.lim
)(
lim
)(
lim
)()(
lim
00
00
y
xFxxF
y
xxХxP
y
yyYyP
y
yFyyF
yf
yy
yy
∆
−∆+
=
∆
∆+<<
=
=
∆
∆+<<
=
∆
−∆+
=
→∆→∆
→∆→∆
Отже,
()
y
xFxxF
yf
y
∆
−
∆
+
=
→∆
)()(
lim
0
. (194)
При ∆у
→
0, ∆х
→
0 з урахуванням функціональної залежності
між Y і Х, помноживши і поділивши дріб (194) на ∆х, дістанемо:
()
.)(
)()()()(
limlimlim
00
0
0
y
yx
y
x
xxf
y
x
x
xFxxF
y
x
x
xFxxF
yf
′
=
∆
∆
∆
−∆+
=
∆
∆
∆
−∆+
→∆→∆
→∆
→∆
Із Y = α(х) знаходимо явно Х =
Ψ
(у). Тоді
(
)
).())(( yyfyf
Ψ
′
Ψ
=
(195)
Якщо
()
xY α=
, де
(
)
x
α
є монотонно спадною функцією (рис. 72),
уу
+
∆
у
х
хх х
0 +
∆
yY =
x
α
()
Рис. 72
