Жлуктенко В. І., Наконечний С. І. Теорія ймовірностей і математична статистика: У 2 ч. - Ч. І. Теорія ймовірностей
Подождите немного. Документ загружается.


148
=
∆
−∆+
∆∆
∆
+
−
∆
+
−
+
∆+∆+
=
→∆
→∆
x
xFxxF
yx
yyxFxxFyxFxxyyF
y
x
)()(
),()(),(),(
lim
0
0
=
∆
−∆+
∆∆
∆+−∆+−+∆+∆+
=
→∆
→∆
→∆
x
xFxxF
yx
yyxFxxFyxFxxyyF
x
y
x
)()(
lim
),()(),(),(
lim
0
0
0
== маємо)(i)(для)69()130(доведенняуючивикористов ,xfx,yf,
∫
∞
∞−
=
dyyxf
yxf
),(
),(
. (156)
Аналогічно доводимо співвідношення
.
),(
),(
)(
),(
)/(
∫
∞
∞−
==
dxyxf
yxf
yf
yxf
yxf (157)
Із (156), (157) дістаємо
f (x, y) = f (x) f (y / x) = f (y) f (x / y). (158)
Для умовних законів розподілу неперервних випадкових величин
умова нормування має такий вигляд:
.1)/(,1)/(
∫∫
∞
∞−
∞
∞−
== dyxyfdxyxf (159)
Якщо випадкові величини Х та Y є незалежними, то
f (x / y) = f (x), f (y / x) = f (y). (160)
У цьому разі (158) набирає вигляду
f (x, y) = f (x) f (y). (161)
Для незалежних випадкових величин Х та Y виконується рівність
F(x, y) = F(x) F(y). (162)
Числові характеристики для умовних законів розподілу ймовір-
ностей:
;)/()/(
∫
∞
∞−
= dxyxxfyXM (163)
;)/()/(
∫
∞
∞−
= dyxyyfxYM
(164)
149
);/()/()/(
22
yXMdxyxfxyXD −=
∫
∞
∞−
(165)
)./()/()/(
22
xYMdyxyfyxYD −=
∫
∞
∞−
(166)
9. Стохaстична залежність
Дві випадкові події називаються незалежними, якщо
<XP((
()
(
)
yYPxXPyYx
<
<=
<
<
I
))(
, або F(x, y) = F(x) F(y).
Для неперервних випадкових величин Х і Y умовy незалежності
можна подати через щільності ймовірностей:
f (x, y) = f (x) f (y).
Умову незалежності можна записати і так:
f (x / y) = f (x), f (y / x) = f (y).
Залежність випадкових величин у певному розумінні
є узагаль-
ненням поняття функціональної залежності. Якщо в разі функціона-
льної залежності між величинами Х та Y кожному значенню Х = х
відповідає певне значення Y = у, то в разі залежності між випадко-
вими величинами Y і Х кожному можливому значенню Х = х відпо-
відає множина значень Y, які характеризуються умовними щільнос
-
тями ймовірності f (y / x).
Отже, залежність між випадковими величинами означає аналітич-
ну залежність щільності умовного розподілу однієї з них від зна-
чень, яких набуває друга величина. Таку залежність називають сто-
хастичною або ймовірнісною. Виявляється вона не лише у зміні
умовних законів розподілу, а й у зміні умовних числових характерис-
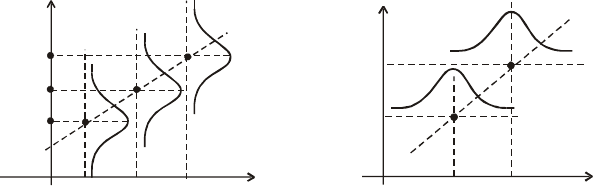
тик: M (X / y), M (Y / x), D (X / y), D (Y / x), тобто умовних математи-
чних сподівань та умовних дисперсій (рис. А—F).
y
MY x
( /
3
)
( / )
( / )
MY x
MY x
2
1
0
xxxx
1 2 3
y
y
y
2
1
0
M
X y MX y x
( /) ( /)
1
2
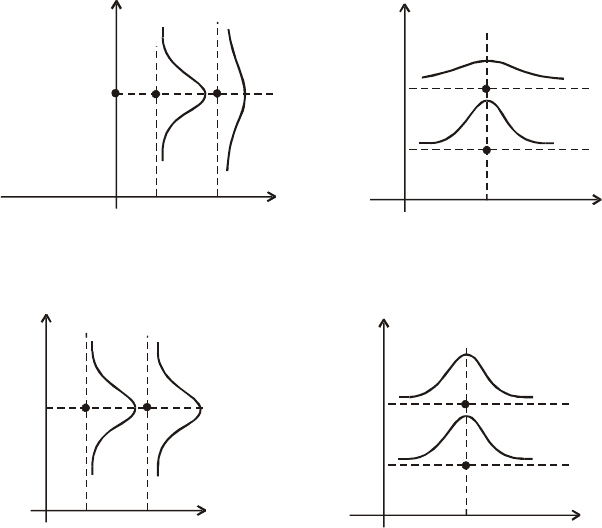
Рис.
А
. Стохастична і кореляційна
залежність між Y та Х,
М
(
Y /
х
)
=
α
(
х
)
Рис.
B
. Стохастична і кореляційна
залежність між Х та Y,
М
(
X
/
у
)
=
β
(
у
)
150
y
( / ) = ( )
MY x Му
0
xxx
1 2
y
у
у
2
1
0
M
Х уМх x
( / ) = ( )
Рис.
С
. Стохастична залежність між
Y та Х, D (Y / х) =
α
(х);
ко
р
еляційний зв’язок відс
у
тній
Рис. D. Стохастична залежність між
Х і Y, D (X / у) =
β
(у);
ко
р
еляційний зв’язок відс
у
тній
y
0
xxx
1 2
( ) = ( )
f
y / x f
x
y
у
у
2
1
0
x
() = ()
fX / fxy
Рис. Е. Незалежні випадкові
величини
Рис.
F
. Незалежні випадкові
величини
Отже, рис. А, В ілюструють те, що кореляційною залежністю між
випадковими величинами Y і Х є функціональна залежність умовних
математичних сподівань М (X / у), М (Y / х) від аргументів у та х:
М (X / у) =
α
(у). (167)
М (Y / х) =
β
(х). (168)
Рівняння (167) та (168) називають рівняннями регресії. Якщо
М (Y / х) = М (y), М (X / у) = М (х), то кореляційна залежність відсут-
ня, але існує стохастична залежність (див. рис. С і D), оскільки змі-
нюються умовні дисперсії. Випадок, коли між Х і Y відсутня стохас-
тична, а отже, і
кореляційна залежність, ілюструють рис. Е і F.
Отже, якщо між випадковими величинами Y і Х існує кореля-
ційна залежність, то між ними обов’язково іcнує й стохастична
залежність. Але за наявності стохастичної залежності між випад-
ковими величинами Х і Y кореляційної залежності між ними може
й не бути.
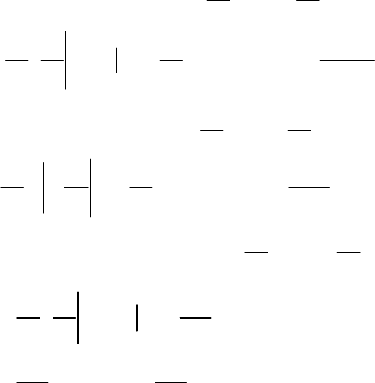
151
Приклад 6.
Задано f (x, y) = 1/48, якщо (x, y) ∈ Ω; f (x, y) = 0, якщо
(x, y) ∉ Ω.
Де
{}
.53,24
≤
≤
−
≤
≤−=Ω yx
Знайти K
ху
, r
ху
.
Розв’язання. Застосовуючи (148) — (152), дістаємо:
(
)
;1
96
812
)35()164(
96
1
248
1
48
1
48
1
),()(
5
3
2
4
2
2
4
5
3
2
4
5
3
5
3
2
4
−=
⋅−
=+−=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=
====
−
−
−− −− −−
∫∫ ∫∫ ∫∫
y
x
dydxxdydxxdydxyxxfXM
;1
96
166
)925)(42(
96
1
248
1
48
1
48
1
),()(
5
3
2
2
4
5
3
2
4
2
4
5
3
2
4
5
3
=
⋅
=−+==
====
−
−
−−−−−−
∫∫∫∫∫∫
y
x
dyydxdxdyydydxyxyfYM
()
;1
192
192
16)12(
192
1
)925)(164(
192
1
248
1
48
1
48
1
),()(
5
3
2
2
4
2
2
4
5
3
2
4
5
3
5
3
2
4
−=−=−=
=−−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
====
−
−
−− −− −−
∫∫ ∫∫ ∫∫
y
x
dyydxxdydxxydydxyxfxyXYM
K
xy
= M (XY) – M (X) M (Y) = –1 – (–1)1 = –1+1 = 0.
Отже, K
xy
= 0, що говорить нам про відсутність кореляційного
зв’язку між випадковими величинами Х та Y.
Оскільки K
xy
= 0, то й r
xy
= 0.
При знайдених f (x), f (y) числові характеристики можна обчислити і
за такими формулами:
;)()(
∫
∞
∞−
= dxxxfXM (169)
;)()()()()(
2222
∫
∞
∞−
−=−= XMdxxfxXMXMXD
(170)
;)()(
∫
∞
∞−
= dyyyfYM (171)
.)()()()()(
2222
∫
∞
∞−
−=−= YMdyyfyYMYMYD (172)
152
Приклад 7. Задано
22
),(
yxyx
eayxf
−+−
= –∞ < х < ∞, –∞ < у < ∞.
Знайти а, М (х / у), М (у / х). Обчислити r
xy
.
Розв’язання. Згідно з умовою нормування (132) маємо:
.
3
2
2
3
2
3
2
2
2
3
2
2
2
3
2
2
3
2
2
2
2
2
2
1
2
2
2
2
1
22
4
3
24
3
24
3
24
3
2
2
4
3
22
2
2
2
2
2
2
2
2
22
22
π
=π
π
=
π
=
π
=
==→==
π
=
=π==
π
=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
=
=−
=
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=→=
∫∫
∫
∫∫
∫∫∫∫
∫∫ ∫∫
∫∫
∞
∞−
−
∞
∞−
−
∞
∞−
−
∞
∞−
∞
∞−
−−
∞
∞−
∞
∞−
−−
∞
∞−
−
∞
∞−
−
∞
∞−
∞
∞−
∞
∞−
⎟
⎠
⎞
⎜
⎝
⎛
−−
∞
∞−
−
−+−
∞
∞−
∞
∞−
−+−
dtedte
dtdytydye
dzedye
dydzeedy
dz
ee
dz
dx
zy
x
dydxeedydxe
dydxe
a
tt
y
z
y
z
y
z
y
y
x
y
yxyx
yxyx
Пуаcсонаінтеграломє
Отже,
π
=
2
3
a
і при цьому
22
2
3
),(
yxyx
eyxf
−+−
π
=
, – ∞ < x < ∞, – ∞ < y < ∞.
Скориставшись (154), знайдемо
.
2
1
2
3
2
2
1
2
3
2
1
2
3
2
2
3
2
2
2
2
3
2
3
),()(
22
2
2
2
2
2
2
22
4
3
4
3
24
3
24
3
2
4
3
xx
t
x
t
x
x
y
x
yxyx
ee
dtee
dt
ee
dt
dy
tx
y
dyeedyedyyxfxf
−−
∞
∞−
−
∞
∞−
−−−
∞
∞−
⎟
⎠
⎞
⎜
⎝
⎛
−−
−
∞
∞−
−+−
∞
∞−
π
=π
π
=
=
π
=
π
=
=
=−
=
=
π
=
π
==
∫∫
∫∫∫
Отже,
2
4
3
2
1
2
3
)(
x
exf
−
π
=
, – ∞ < х < ∞.
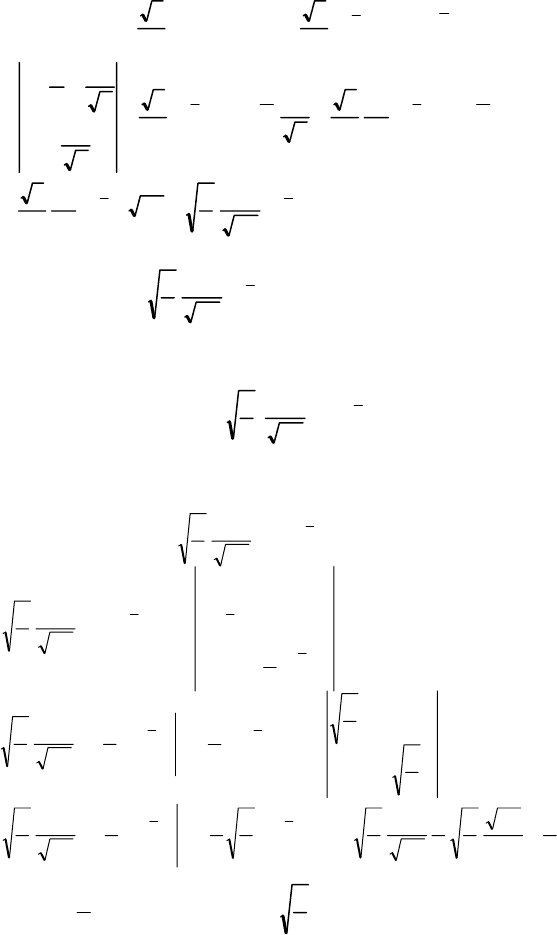
153
Далі, застосувавши (155), знайдемо:
.
2
1
2
3
2
2
1
2
3
2
1
2
3
2
2
3
2
2
2
2
3
2
3
),()(
22
2
2
2
2
2
2
22
4
3
4
3
24
3
24
3
2
4
3
yy
t
y
t
y
y
x
y
yxyx
ee
dtee
dt
ee
dt
dx
t
y
x
dxeedxedxyxfyf
−−
∞
∞−
−
∞
∞−
−−−
∞
∞−
⎟
⎠
⎞
⎜
⎝
⎛
−−
−
∞
∞−
−+−
∞
∞−
π
=π
π
=
=
π
=
π
=
=
=−
=
=
π
=
π
==
∫∫
∫∫∫
Отже,
2
4
3
2
1
2
3
)(
y
eyf
−
π
=
, – ∞ < у < ∞.
Знайдемо основні числові характеристики. Згідно з (137) — (142)
маємо:
0
2
1
2
3
)()(
2
4
3
=
π
==
−
∞
∞−
∞
∞−
∫∫
dxexdxxxfXM
x
,
оскільки підінтегральна функція є непарною, а межі інтегрування симе-
тричні відносно нуля.
.
3
2
2
2
3
2
3
2
2
1
2
3
2
3
2
3
2
3
2
2
1
2
3
2
3
2
2
3
3
2
3
2
2
1
2
3
2
3
2
,
2
1
2
3
2
2
1
2
3
)()()(
0
2
0
4
3
0
4
3
0
4
3
4
3
4
3
4
3
2
4
3
222
2
22
2
22
2
=
π
π
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+−
π
=
=
=→
→=
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+−
π
=
=
−=→
→=
==
=
π
=
=
π
===
∫
∫
∫
∫∫
∞
−
∞
−
∞
−
∞
−
−
−
∞
∞−
−
∞
∞−
−
∞
∞−
dtexe
dtdx
tx
dxexe
ev
dvdxxe
dxduxu
dxex
dxexdxxfxXMXD
t
x
xx
x
xx
x
Отже,
3
2
)( =XD
, звідки
3
2
)( =σ=σ
x
X
.
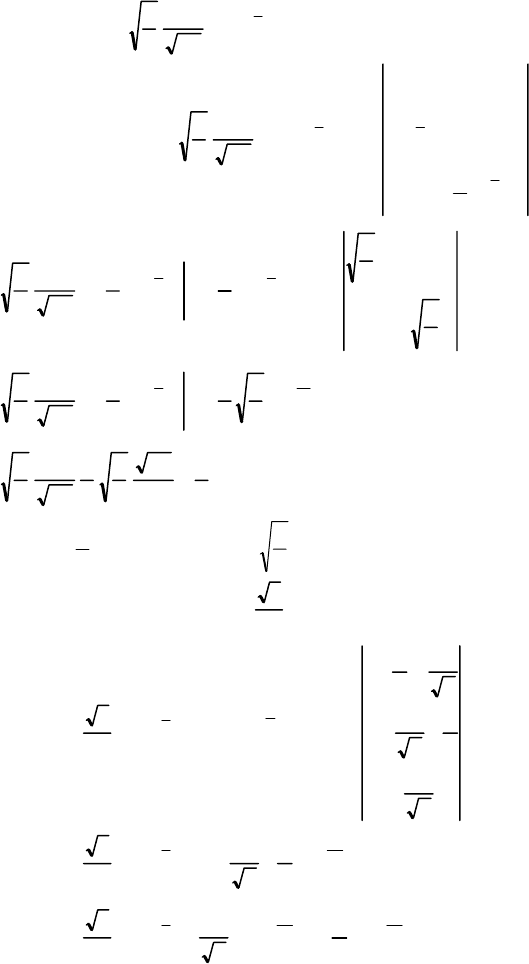
154
∫∫
∞
∞−
−
∞
∞−
=
π
== .0
2
1
2
3
)()(
2
4
3
dyyedyyyfYM
y
.
3
2
2
2
3
2
3
2
2
1
2
3
2
3
2
3
2
3
2
2
1
2
3
2
3
2
2
3
3
2
3
2
2
1
2
3
2
3
2
,
2
1
2
3
)()()(
0
2
0
4
3
0
4
3
0
4
3
4
3
4
3
4
3
222
2
2
22
2
22
=
π
π
=
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+−
π
=
=
=→
→=
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+−
π
=
=
−=→
→=
==
=
π
===
∫
∫
∫∫
∞
−
∞
−
∞
−
∞
−
−
−
∞
∞−
−
∞
∞−
dteye
dtdy
ty
dyeye
ev
dvdyye
dyduyu
dyeydyyfyYMYD
t
y
yy
y
yy
Отже,
.
3
2
)( =YD Тоді
3
2
)( =σ=σ
y
Y .
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
π
=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
π
=
=
=
+=
=−
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
π
=
=
π
==
∫∫∫
∫∫
∫∫
∫∫∫∫
∞
∞−
−
∞
∞−
−
∞
∞−
−
∞
∞−
−
∞
∞−
−
∞
∞−
⎟
⎠
⎞
⎜
⎝
⎛
−−
∞
∞−
−
∞
∞−
∞
∞−
−+−
∞
∞−
∞
∞−
dydze
y
dzzeye
dydze
y
z
ye
dz
dx
y
z
x
z
y
x
dydxxeye
dydxexydydxxyfxyXYM
zz
y
z
y
y
x
y
yxyx
224
3
24
3
2
4
3
22
2
2
2
2
2
22
2
2
1
2
3
2
2
2
3
2
2
2
2
2
2
3
2
3
)()(

155
.
3
1
2
2
3
2
3
2
2
3
3
2
2
3
3
2
2
3
3
2
3
2
2
3
3
2
,,
2
3
2
2
1
2
3
22
2
1
2
3
0
4
3
0
4
3
0
4
3
4
3
4
3
0
4
3
2
0
4
3
2
4
3
2
222
22
2
22
=
π
π
==→==
=
π
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+−
π
=
=
−=→=
==
=
π
=
=π
π
=π
π
=
∫∫
∫
∫∫
∞
−
∞
−
∞
−
−−
∞
−
∞
−
∞
∞−
−
dtdyty
dyedyeye
evdvdyye
dyduyu
dyey
dyeydyey
yyy
yy
y
yy
Таким чином, дістали
;
3
1
)()()( =−= YMXMXYMK
xy
2
1
3
2
3
2
3
1
==
σσ
=
yx
xy
xy
K
r
.
Визначимо умовні щільності ймовірностей, скориставшись (156) і (157):
.
2
1
2
2
1
2
3
2
3
)(
),(
)/(
22
2
22
4
1
4
3
yxyx
x
yxyx
e
e
e
xf
yxf
xyf
−+−
−
−+−
π
=
π
π
==
Отже,
2
2
1
2
2
)/(
⎟
⎠
⎞
⎜
⎝
⎛
−−
π
=
xy
eyxf
, – ∞ < у < ∞.
.
2
1
2
2
1
2
3
2
3
)(
),(
)/(
2
2
22
)
2
1
(
4
3
yx
y
yxyx
e
e
e
yf
yxf
yxf
−−
−
−+−
π
=
π
π
==
Звідси
2
)
2
1
(
2
1
2)/(
yx
eyxf
−−
π
=
, – ∞ < х < ∞.
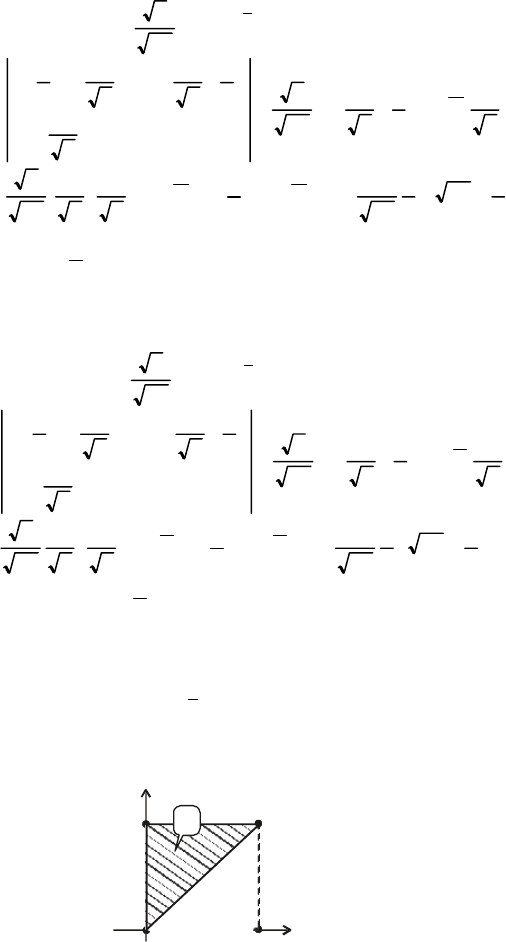
156
.
2
1
2
2
1
2
1
2
1
2
1
2
1
2
2
2
2
1
22
2
2
2
1
22
2
1
2
2
)/()/(
22
2
2
1
22
2
2
yydzeydzze
dz
ey
z
dz
dx
y
z
x
z
yx
dxxedxyxxfyXM
zz
z
yx
=π
π
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
π
=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
π
=
=
+=→=−
=
=
π
==
∫∫
∫
∫∫
∞
∞−
−
∞
∞−
−
∞
∞−
−
∞
∞−
∞
∞−
⎟
⎠
⎞
⎜
⎝
⎛
−−
Отже,
yyXM
2
1
)/( =
є лінійною функцією регресії відносно аргу-
менту у.
Аналогічно маємо:
.
2
1
2
2
1
2
1
2
1
2
1
2
1
2
2
2
2
1
22
2
2
2
1
2
,
2
2
1
2
2
)/()/(
22
2
2
1
22
2
2
xxdtexdtte
dt
ex
t
dt
dy
x
t
y
t
xy
dyyedyxyyfxYM
tt
t
xy
=π
π
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
π
=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
π
=
=
+=→=−
=
=
π
==
∫∫
∫
∫∫
∞
∞−
−
∞
∞−
−
∞
∞−
−
∞
∞−
∞
∞−
⎟
⎠
⎞
⎜
⎝
⎛
−−
Таким чином
yyXM
2
1
)/( =
також є лінійною функцією регресії ві-
дносно аргументу х.
Приклад 8. Задано
)(),( yxayxf
+
=
, якщо
Ω
∈
),( yx
;
0),( =yxf
, якщо
Ω∈),( yx
, де
{
}
.1,10 ≤
≤
≤
≤
=
Ω
yxx
Знайти а і r
xy.
Розв’язання. Область Ω зображено на рис. 68.
y
1
0 1
x
(1; 1)
Ω
Рис. 68
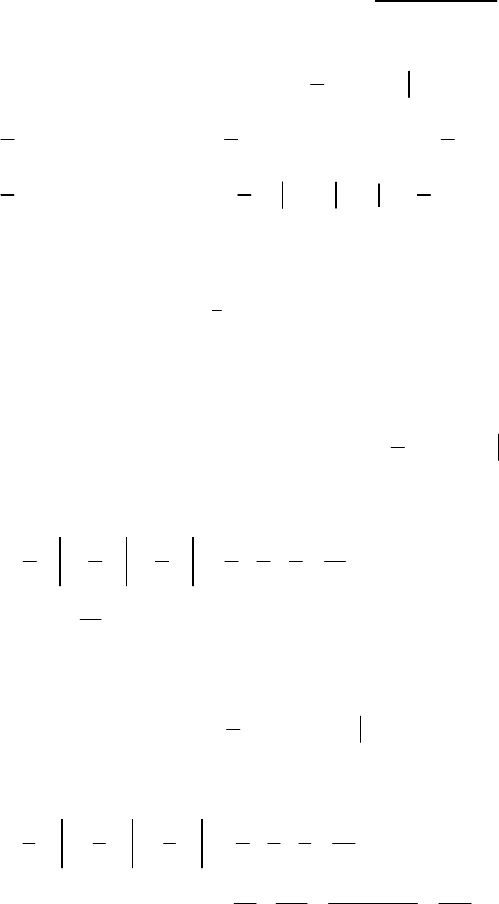
157
За умовою нормування (131) обчислюємо значення а:
()
[]
()
.
2
1
2
1
32
2
1
)132(
2
1
)412(
2
1
)()1(
2
1
)(
2
1
)()(
)(
1
1)(1),(
1
0
1
0
3
1
0
2
1
0
1
0
1
0
2
1
0
1
0
222
1
0
22
1
0
1
2
1
0
1
0
11
1
0
1
1
0
1
=+−=
⎟
⎠
⎞
⎜
⎝
⎛
+−=
=+−=−++=+−+=
=+=
⎟
⎠
⎞
⎜
⎝
⎛
+=+→
→
+
=→=+→=
∫∫∫
∫∫∫
∫∫∫∫∫
∫∫ ∫ ∫
∫∫
Ω
xxxdxdxxdxx
dxxxdxxxxdxxxx
dxyxdxdyyxdydxyx
dydxyx
adydxyxadydxyxf
x
xx
x
x
Отже, а = 2.
Тоді
)(2),( yxyxf += , якщо
Ω
∈
),( yx
,
0),( =yxf , якщо Ω∈),( yx , де
{
}
1,10
≤
≤
≤
≤
=
Ω
yxx .
Числові характеристики знаходимо за (137) — (142):
()
[]
.
12
5
2
1
4
3
3
2
2
1
4
3
3
2
32)32(4)1(
)(
2
1
2)(2)(2
)(2),()(
1
0
2
1
0
4
1
0
3
1
0
1
0
1
0
1
0
3232
1
0
22
1
0
1
2
1
0
1
0
11
1
0
1
=+−=+−=
=+−=+−=−+=
=+=
⎟
⎠
⎞
⎜
⎝
⎛
+=+→
=+==
∫∫∫∫∫
∫∫∫∫∫
∫∫ ∫ ∫
Ω
xxx
dxxdxxdxxdxxxxdxxxx
dxyxxdxdyyxxdydxyxx
dydxyxxdydxyxxfXM
x
xx
x
12
5
)( =XM
.
() ()
.
30
7
3
1
5
3
2
1
3
1
5
3
3
1
32)32(
4)1()(
2
1
2)(2
)(2),()(
1
0
3
1
0
5
1
0
4
1
0
1
0
1
0
2
1
0
43243
1
0
222
1
0
1
0
1
22
1
2
1
0
1
222
=+−=+−=
=+−=+−=
=−+=+=
⎟
⎠
⎞
⎜
⎝
⎛
+=
=+==
∫∫∫∫
∫∫∫∫
∫∫ ∫ ∫
Ω
xxx
dxxdxxdxxdxxxx
dxxxxdxyxxdxdyyxx
dydxyxxdydxyxfxXM
x
x
x
720
43
4320
7501008
144
25
30
7
)()()(
22
=
−
=−=−= XMXMXD .
