Жлуктенко В. І., Наконечний С. І. Теорія ймовірностей і математична статистика: У 2 ч. - Ч. І. Теорія ймовірностей
Подождите немного. Документ загружается.

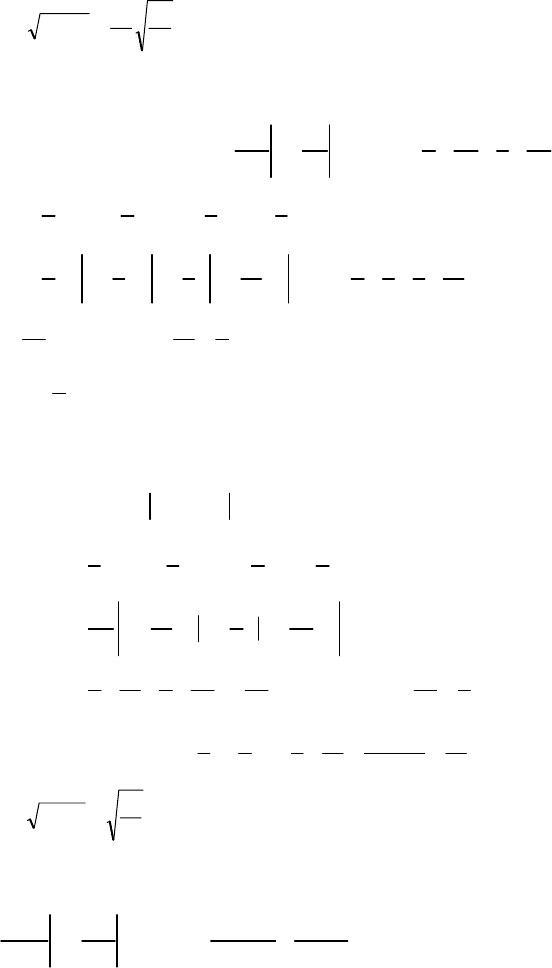
158
.244,0
5
43
12
1
)( ≈==σ XD
x
.
4
3
12
9
)2836(
24
2
12
1
3
1
8
1
4
1
2
12
1
3
1
8
1
4
1
2
3
1
3
1
2
1
2
1
2
33
1
22
2
32
2)(2
)(2),()(
1
0
4
1
0
1
0
4
1
0
2
1
0
1
0
3
1
0
1
0
3
1
0
1
0
33
1
3
1
2
1
0
1
0
2
1
0
1
==−+−=
=
⎟
⎠
⎞
⎜
⎝
⎛
−+−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+−=
=
⎟
⎠
⎞
⎜
⎝
⎛
−+−=
=
⎟
⎠
⎞
⎜
⎝
⎛
−+−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+=
⎟
⎠
⎞
⎜
⎝
⎛
+=
=+==
∫∫∫∫
∫∫∫∫
∫∫ ∫ ∫
Ω
xxxx
dxxdxdxxdxx
dx
xxx
dx
yxy
dxdyyxy
dxdyyxydxdyyxyfYM
xx
x
4
3
)( =YM
.
.
5
3
30
18
)315410(
60
2
20
1
4
1
15
1
6
1
2
20
1
4
1
15
1
6
2
4
1
4
1
3
1
3
1
2
)3/4/13/3/(2)4/3/(2
))((2)(2),()(
0
1
5
1
0
1
0
5
0
1
2
1
0
4
1
0
1
0
4
1
0
1
0
44
1
0
1
4
1
3
1
0
1
32
1
0
1
222
==−+−=
⎟
⎠
⎞
⎜
⎝
⎛
−+−=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+−=
=
⎟
⎠
⎞
⎜
⎝
⎛
−+−=
=−+−=+=
=+=+==
∫∫∫∫
∫∫
∫∫∫∫∫∫
Ω
xxx
x
dxxdxdxxdxx
dxxxxdxyxy
dxdyyxydxdyyxydxdyyxfyYM
xx
xx
.
16
3
16
4548
16
9
5
3
4
3
5
3
)()()(
2
22
=
−
=−=
⎟
⎠
⎞
⎜
⎝
⎛
−=−= YMYMYD
433,0
16
3
)( ≈==σ YD
y
.
∫∫
∫∫∫∫∫∫
=
⎟
⎠
⎞
⎜
⎝
⎛
−
+
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+=
=+=+==
Ω
1
0
1
0
442
1
3
1
22
1
0
1
22
1
0
1
32
2
32
2
))((2)(2),()(
dx
xxxx
dx
xyyx
dxdyxyyxdxdyyxxydxdyyxfxyXYM
xx
xx
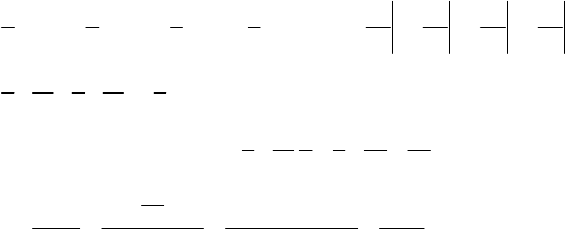
159
.
3
1
15
1
6
1
10
1
6
1
2
156106
2
3
1
3
1
2
1
2
1
2
1
0
5
1
0
2
1
0
5
1
0
3
1
0
4
1
0
1
0
4
1
0
2
=
⎟
⎠
⎞
⎜
⎝
⎛
−+−=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+−=
⎟
⎠
⎞
⎜
⎝
⎛
−+−=
∫∫∫∫
xxxx
dxxdxxdxxdxx
.
48
1
48
15
3
1
4
3
12
5
3
1
)()()( =−=−=−= YMXMXYMK
xy
.197,0
071,5
1
244,0433,048
1
244,0433,0
48
1
≈≈
⋅⋅
=
⋅
=
σσ
=
yx
xy
xy
K
r
Отже,
K
ху
= 1,48; R
xy
≈ 0,197.
10. Система довільного числа
випадкових величин
10.1. Функція розподілу системи
n випадкових величин
Функцією розподілу n випадкових величин називається така фу-
нкція від n аргументів (х
1
, х
2
… х
п)
, яка визначає ймовірність спільної
одночасної появи подій
((Х
1
< х
1
) I (X
2
< х
2
) I (X
3
< х
3
) I … I (X
n
< х
1n
):
).()...,,,(
1
21
ii
n
i
n
xXPxxxF <=
=
I
(173)
Ця функція має всі властивості функції розподілу ймовірностей
одного та двох аргументів.
Якщо принаймні один з аргументів х
і
→
–
∞
, то функція роз-
поділу ймовірностей системи п випадкових величин прямує до нуля.
Якщо із системи х
1
, х
2
,… х
п
виділимо деяку підсистему х
1
, х
2
,…, х
k
(k < n), то функцію розподілу для цієї підсистеми дістанемо, коли
решта аргументів прямуватиме до
∞
:
)....,,...,,()...,,,(
2121
∞
∞
∞
=
kk
xxxFxxxF
Зокрема, дістанемо функцію розподілу одного аргументу, якщо
всі аргументи, окрім х
1
, спрямуємо до
∞
:
)....,,,,()(
11
∞
∞
∞
=
xFxF
Якщо всі аргументи спрямувати до
∞
, то 1),...,,(
=
∞
∞
∞
F .

160
10.2. Щільність імовірностей системи
n випадкових величин
Щільність імовірностей системи п випадкових величин є функція
n
n
n
n
xxx
xxxF
xxxxf
∂∂∂
∂
=
...
)...,,,(
)...,,,,(
21
21
321
(174)
Умова нормування для системи п неперервних випадкових величин
.1...)...,,,(...
2121∫∫ ∫
∞
∞−
∞
∞−
∞
∞−
=
nn
dxdxdxxxxf (175)
Щільність імовірностей для деякої підсистеми (х
1
, х
2
,… х
k
) сис-
теми (х
1
, х
2
,… х
п
), де k < n подається у вигляді
....)...,,,(...)...,,,(
212121 ∫∫ ∫
∞
∞−
∞
∞−
∞
∞−
++
=
nkknk
dxdxdxxxxfxxxf (176)
Наприклад,
....)...,,,(...)(
32211 ∫∫ ∫
∞
∞−
∞
∞−
∞
∞−
=
nn
dxdxdxxxxfxf (177)
Умовна щільність підсистеми (х
1
, х
2
,…, х
k
) системи (х
1
, х
2
,…, х
п
)
(k < n) визначається за формулою
),...,,(
),...,,(
)...,,,/...,,,(
21
21
2121
nkk
n
nkkk
xxxf
xxxf
xxxxxxf
++
++
= . (178)
Якщо випадкові величини системи (х
1
, х
2
,…, х
п
) є незалежними, то
).(...)()(),...,,(
2121
nn
xfxfxfxxxf
=
(179)
10.3. Числові характеристики системи
n випадкових величин
;...)...,,,(...)(
2121
∫∫ ∫
∞
∞−
∞
∞−
∞
∞−
=
nnii
dxdxdxxxxfxxM (180)
;)(...)...,,,(...)(
2
2121
2
∫∫ ∫
∞
∞−
∞
∞−
∞
∞−
−=
inn
i
i
xMdxdxdxxxxfxxD
(181)
).()(...)...,,,(...
2121
jinnjiijxx
xMxMdxdxdxxxxfxxKK
ji
−==
∫∫ ∫
∞
∞−
∞
∞−
∞
∞−
(182)
При цьому виконується рівність
jiij
KK
=
. (183)
Коли i = j, маємо:
.)(
2
i
ijjii
xDKK σ=== (184)

161
Усі кореляційні моменти і дисперсії розміщують у вигляді квад-
ратної таблиці, яка називається кореляційною матрицею системи п
випадкових величин і має такий вигляд:
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
nnnnn
n
n
n
kkkk
kkkk
kkkk
kkkk
...
......
...
.........
...
...
321
3333231
2232221
1131211
. (185)
Елементи кореляційної матриці симетрично розміщені відносно
її головної діагоналі. Оскільки
jiij
KK
=
,
2
i
it
K σ=
, заповнюють лише
половину кореляційної матриці. І в цьому випадку вона набуває та-
кого вигляду:
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
σ
σ
σ
σ
2
3
2
3
223
2
2
11312
2
1
......
...
...
...
n
n
n
n
k
kk
kkk
. (186)
Якщо
0=
ij
K для всіх i = 1, …, n; j = 1, …, n, то кореляційна мат-
риця набирає такого вигляду:
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
σ
σ
σ
σ
2
2
3
2
2
2
1
...
0
...
...
0...0
0...00
n
. (187)
Таку матрицю називають діагональною.
За відомими кореляційними моментам
ij
K визначаємо парні ко-
ефіцієнти кореляції:
.
ji
ij
ij
K
r
σσ
=
(188)
При i = j маємо
1=
ij
r
.
Із парних коефіцієнтів кореляції утворюють так звану нормовану
квадратну матрицю:
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
1
......
...1
...1
...1
3
223
11312
n
n
n
r
rr
rrr
. (189)
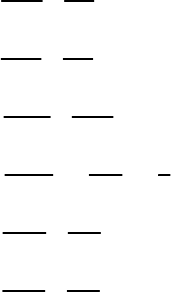
162
Приклад 9.
Дано кореляційну матрицю системи (х
1
, х
2
, …, х
п
):
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
−
−
25
216
8,014
8,015,01
.
Побудувати нормовану кореляційну матрицю.
Розв’язання. Згідно зі (188) маємо:
;25,0
21
5,0
21
12
12
=
⋅
=
σσ
=
K
r
;25,0
41
1
31
13
13
=
⋅
=
σσ
=
K
r
;16,0
51
8,0
41
14
14
−=
⋅
−
=
σσ
=
K
r
;125,0
8
1
42
1
32
23
23
−=−=
⋅
−=
σσ
=
K
r
;08,0
52
8,0
42
24
24
=
⋅
=
σσ
=
K
r
1,0
54
2
43
34
34
=
⋅
=
σσ
=
K
r
.
Нормована кореляційна матриця подається у вигляді
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−
−
1
1,01
08,0125,01
16,025,025,01
.
Теоретичні запитання до теми
?
1. Означення багатовимірної випадкової величини.
2. Означення закону розподілу багатовимірної випадкової
величини.
3. Основні числові характеристики для системи двох дис-
кретних випадкових величин.
4. Що визначає кореляційний момент?
5. Чому дорівнює K
ху
?
6. Коефіцієнт кореляції та його властивості.
163
7. Якщо K
ху
= 0, то чому дорівнює r
ху
?
8. Що називається умовним законом розподілу Y / х?
9. Умови нормування для системи двох дискретних випад-
кових величин.
10. Що називається умовним законом розподілу X / у?
11. Чому дорівнюють М (X / у), М (Y / х)?
12. Означення функції розподілу системи двох випадкових
величин.
13. Довести, що F(x
2
, y) ≥ F(x
1
, y).
14. Довести, що F(x, y
2
) ≥ F(x, y
1
).
15. Як обчислити P(a < X <b, c < Y < d)?
16. Чому дорівнює
),(lim yxF
x
∞→
?
17. Чому дорівнює
),(lim yxF
y ∞→
?
18. Чому дорівнює
),(lim yxF
y
x
∞→
∞→
?
19. Чому дорівнює
),(lim yxF
x −∞→
,
),(lim yxF
y −∞→
, ),(lim yxF
y
x
−∞→
−∞→
?
20. Означення щільності ймовірностей системи двох непе-
рервних випадкових величин.
21. Довести, що
∫∫
∞
∞−
∞
∞−
= ...),( dydxyxf .
22. Довести, що
...),( =
∫∫
∞−∞−
x
y
dydxyxf .
23. Чому дорівнює
...),( =
∫∫
b
a
d
c
dydxyxf
, якщо
),( dycbxa
<
<
<<=Ω ?
24. Чому дорівнює
...),( =
∫∫
D
dydxyxf
, якщо
{}
Ω
⊂
<
<
<<= dycbxaD , ?
25. Чому дорівнює =
∫∫
Ω
dydxyxxf ),( ?
26. Чому дорівнює
∫∫
Ω
=dydxyxyf ),( ?
27. Формула для D (X) випадкової величини X, що утворює
систему (X, Y), має вигляд… .
28. K
ху
для системи двох неперервних випадкових величин
(X, Y) обчислюється за формулою… .
29. D (Y) для випадкової величини Y, що утворює систему
двох неперервних випадкових величин (X, Y), обчислюється
за формулою… .

164
30. Чому дорівнює
∫
∞
∞−
= ...),( dyyxf ?
31. Чому дорівнює
∫
∞
∞−
= ...),( dxyxf
?
32. Довести, що
1≤
xy
r
.
33. Як знайти f (X / y)?
34. М (X / у) обчислюється за формулою… .
35. Чому дорівнює f (Y / x)?
36. М (X / x) обчислюється за формулою… .
37. Якщо випадкові величини Х і Y є незалежними, то f (x, y)
обчислюється за формулою… .
38. Якщо випадкові величини Х і Y є
незалежними, то
F (x, y) = … .
39. Якщо випадкові величини некорельовані, то чи будуть
вони й незалежними і навпаки?
40. Що називається функцією розподілу системи п випадко-
вих величин?
41. Як визначається щільність iмовірностей системи п випа-
дкових величин?
42. Як визначається щільність iмовірностей системи (х
1
,
х
2
, … х
k
), що входить до (х
1
, х
2
, … х
п
)?
43. Основні числові характеристики системи п випадкових
величин.
44. Чому дорівнює
ij
K ?
45. Чому дорівнює
ij
K , якщо i = j?
46. Парні коефіцієнти кореляції обчислюються за форму-
лою… .
47. Чому дорівнює
ij
r ?
48. Що називають кореляційною матрицею системи п випа-
дкових величин?
49. Що називають нормованою кореляційною матрицею?
Приклади до теми
1. Імовірність появи випадкової події в кожному з чотирьох неза-
лежних експериментів є величиною сталою і дорівнює 0,9. Розгля-
даються дві випадкові величини: Х — число появи випадкової події
в результаті цих експериментів; Y — число експериментів, при яких
подія не наставала.
Обчислити: M (X);
σ (X); M (Y); σ (Y); K
ху
; r
ху
.
Відповідь. M (X) = 3,6;
σ (X) = 0,6; M (Y) = 0,4; σ (Y) = 0,6; K
ху
=
= – 0,36; r
ху
= –1.
165
2. Задано f (x, y) = a, якщо (x, y) ∈ Ω, f (x, y) = 0, якщо (x, y) ∉ Ω,
де
Ω = (– 6 ≤ x ≤ 2, –3 ≤ y ≤ 5). Знайти а. Обчислити r
ху
, P(– 4 < x < 1;
–2 < y < 4).
Відповідь. а = 1/64, r
ху
= 0, P(– 4 < x < 1; –2 < y < 4) = 15 / 32.
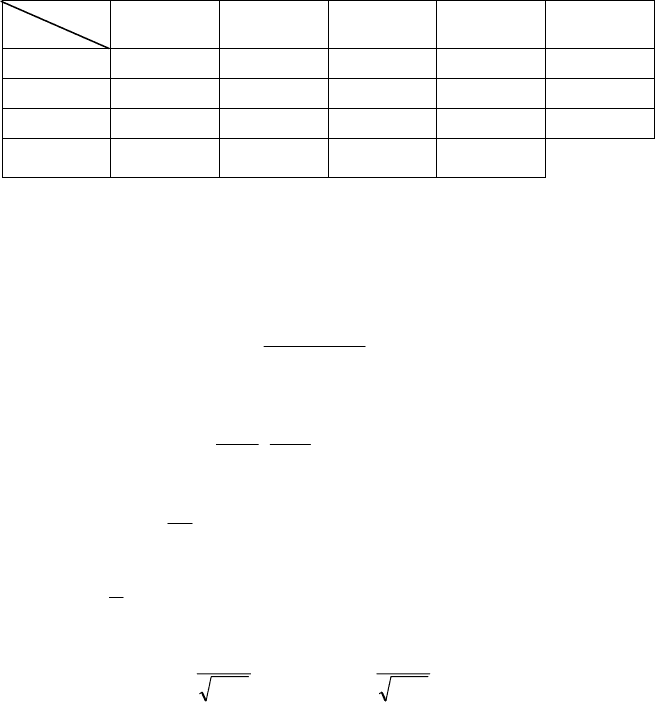
3. Закон системи двох дискретних випадкових величин (X, Y) за-
даний таблицею:
Х
Y
2 4 6 8
i
y
p
– 6 0,1a 0,5a 0,4а a
– 4 0,9a 0,4a 0,5а 0,2a
– 2 a 2,1a 1,1а 1,8a
i
x
p
Обчислити r
ху
, М (Х / y = 4), М (Y / x = –2).
Відповідь: r
ху
= – 0,009, М (Х / y = 4) = –3,3, М (Y / x = –2) = 5,23.
4. Щільність iмовірностей системи випадкових величин задана
виразом f (x, y) = a cos (x – y), якщо (x, y) ∈ Ω, f (x, y) = 0, якщо
(x, y)
∉Ω, де
{}
2/0,2/0
π
≤
≤
π
≤≤=Ω yx . Визначити а і r
ху
.
Відповідь. а = 1 / 2,
328
168
2
2
−π+π
+π−π
=
xy
r .
5. Щільність імовірностей двох випадкових величин (Х, Y) задано
виразом
2
)1(
8
)3(
22
),(
−
−
+
−
=
yx
aeyxf
, – ∞ < х < ∞, – ∞ < y < ∞.
Знайти а; М (х); М (у);
σ
х
;
σ
у
; r
xy.
.
Відповідь.
π
=
4
1
a
;
3)(
−
=
xM
; 0,1,2,1)( =
=
σ
=
σ
=
xyyx
ryM .
6. За заданою щільністю ймовірностей
∞<<∞−∞<<∞−
π
=
++−
y,x,e
1
)y,x(f
)y5xy2x(5,0
22
знайти f (x), f (y).
Відповідь.
22
24,0
5,0
1
)(,
5,2
1
)(
yx
eyfexf
−−
π
=
π
=
.
7. Виготовлені на заводі циліндри сортуються за відхиленням їх
внутрішніх діаметрів від номінального розміру на чотири групи зі
значеннями 0,01; 0,02; 0,03; 0,04 мм і за овальністю на чотири групи зі
значенями 0,002; 0,004; 0,006; 0,008 мм. Спільний розподіл цих від-
хилень Х — діаметра і Y — овальності циліндрів наведено в таблиці:
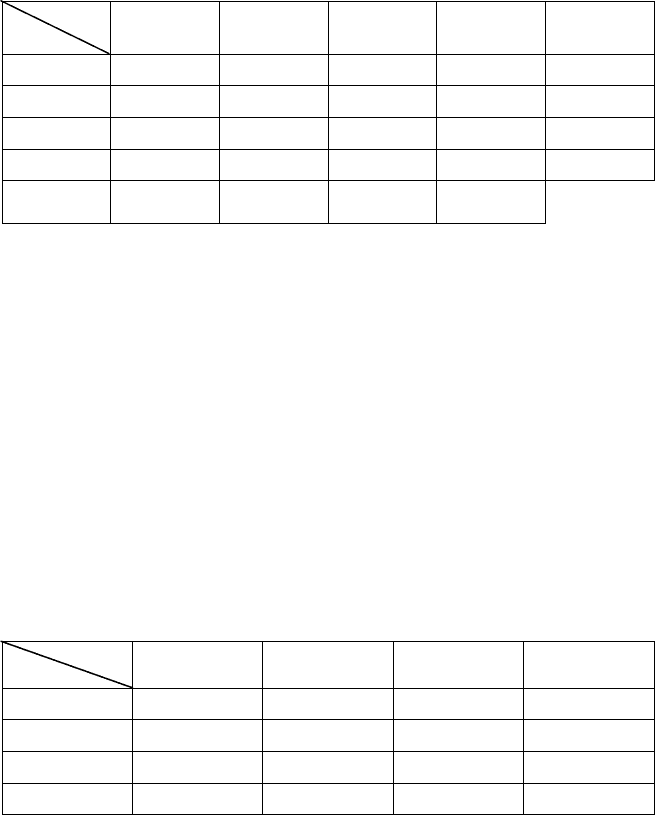
166
Х
Y
0,01 0,02 0,03 0,04
i
y
p
0,002 0,01 0,02 0,04 0,04
0,004 0,03 0,24 0,15 0,06
0,006 0,04 0,1 0,08 0,08
0,008 0,02 0,04 0,03 0,02
j
x
p
Знайти r
xy
.
Відповідь. r
xy
= 0,141.
8. П’ять приладів випробовують на надійність. Імовірність того,
що окремо взятий прилад витримає режим випробування, дорівнює
0,85. Нехай Х — число приладів, які витримають випробування, а Y —
число приладів, які не витримають їх. Побудувати закон спільного ро-
зподілу Х і Y і обчислити K
xy
, r
xy
.
Відповідь. K
xy
= – 0,6375, r
xy
= – 1.
9. У трьох посудинах містяться однотипні вироби. У першій по-
судині міститься 6 стандартних і 4 браковані вироби; у другій — 8
стандартних і 2 браковані, а у третій — 9 стандартних і 1 бракова-
ний виріб. Із кожної посудини навмання беруть по одному виробу.
Нехай Х — поява числа стандартних виробів серед трьох навмання
взятих, а Y — поява відповідного
числа бракованих. Побудувати за-
кон розподілу Х і Y і обчислити K
xy
, r
xy
.
Відповідь.
Х
Y
0 1 2 3
0 0 0 0 0,432
1 0 0 0,444 0
2 0 0,116 0 0
3 0,008 0 0 0
K
xy
= 0,21, r
xy
= 0,148.
10. Брак продукції заводу внаслідок дефекту А становить 3%, а
внаслідок дефекту В — 4,5%. Стандартна продукція становить 95%.
Знайти кореляційний момент і коефіцієнт кореляції між дефектами
А і В.
Відповідь. K
АВ
= 0,02365, r
АВ
= 0,67.

167
11. Задана щільність імовірностей:
Ω
∈
+= ),(),(sin5,0),( YXyxyxf якщо ;
Ω∈= ),(,0),( YXyxf якщо
,
де
.
2
0,
2
0
⎭
⎬
⎫
⎩
⎨
⎧
π
≤≤
π
≤≤=Ω yx
Побудувати кореляційну матрицю.
Відповідь.
.
188,0046,0
046,0188,0
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
=
ij
K
12. Система випадкових величин (Х, Y) має щільність імовірностей
)25)(16(
),(
222
yx
a
yxf
++π
=
,
якщо (Х, Y)
∈ Ω де Ω = (– ∞ < х < ∞; – ∞ < у < ∞).
Знайти а і F(x, y), r
xy
.
Відповідь: а = 20,
()
⎟
⎠
⎞
⎜
⎝
⎛
+
π
⎟
⎠
⎞
⎜
⎝
⎛
+
π
=
2
1
5
arctg
1
2
1
4
arctg
1
,
y
x
yxF
, r
xy
= 0.
13. За заданою функцією розподілу ймовірностей
(
)
(
)
yx
eeyxF
54
11),(
−−
−−= ,
0,0 ≥≥ yx
знайти f (x, y) і r
xy
.
Відповідь.
()
yx
eyxf
54
20,
−−
=
, 0,0 ≥≥ yx ; r
xy
= 0.
14. За заданою функцією розподілу ймовірностей системи (Х, Y)
маємо:
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎨
⎧
>>
≤<−>
+
≤<−≤<−
++
>≤<−
+
≤−≤
=
.4,2,1
;42,2,
6
2
;42,26,
48
)2)(6(
;4,26,
8
6
;2,6,0
),(
yx
yx
y
yx
yx
yx
x
yx
yxF
Знайти K
ху
. Обчислити )31,12(
<
<
−
<
<
−
yxP .
Відповідь. K
ху
= 0; 25,0
4
1
)31,12( ==<<−<<− yxP
.
