Жлуктенко В. І., Наконечний С. І. Теорія ймовірностей і математична статистика: У 2 ч. - Ч. І. Теорія ймовірностей
Подождите немного. Документ загружается.

188
Отже,
()
(
)
.
96
8
1
2
−
−=
z
zF
Таким чином, загальний вигляд функції розподілу ймовірностей бу-
де такий:
()
()
()
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎨
⎧
>
≤<
−
−
≤<
+
≤<−
+
−≤
=
.8,1
;22,
96
8
1
;20,
8
3
;06,
96
6
;6,0
2
2
z
z
z
z
z
z
z
z
zF
Тоді щільність імовірностей матиме вигляд
()
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎨
⎧
>
≤<
−
≤<
≤<−
+
−≤
=
.8,0
;82,
48
8
;20,
8
1
;06,
48
6
;6,0
z
z
z
z
z
z
z
zf
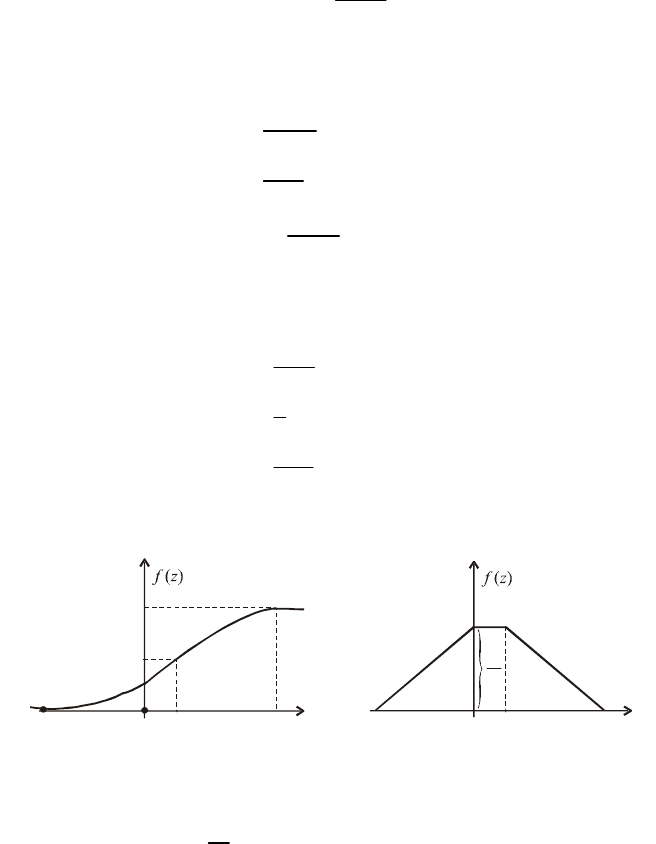
Графіки F (х), f (х) зображені на pис. 80 і 81.
–
6 0 2 8
z
1
0,5
–
6 0 2 8
z
1
8
Рис. 80 Рис. 81
4.2. Знаходження F (z), f (z),
якщо
()
ZXY
Х
Y
Z
==
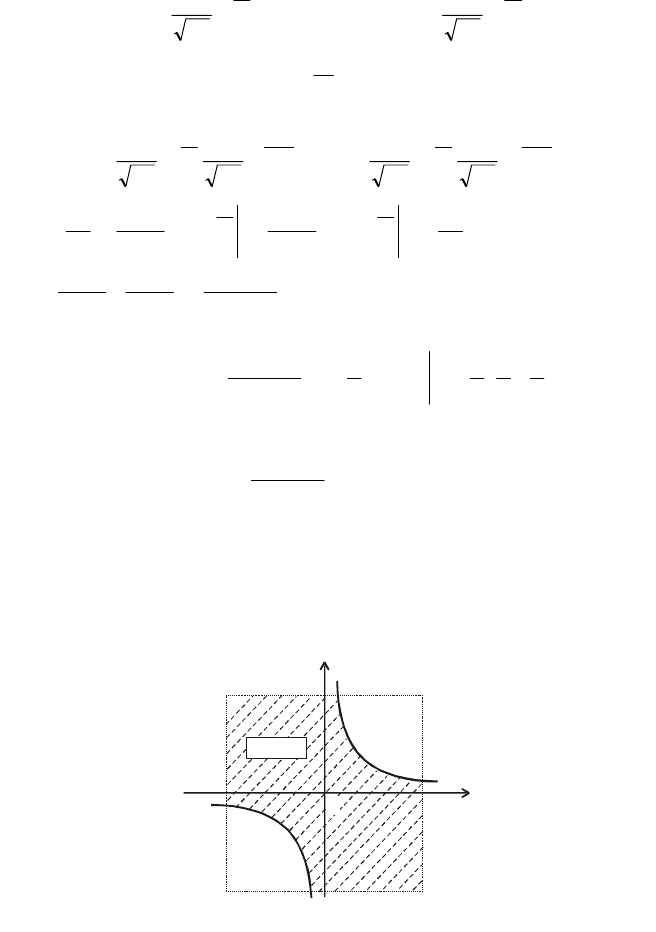
Оскільки пряма Y = ZХ ділить площину хОу на дві непересічені
області, зображені на рис. 82.
190
Приклад 6. Задано
()
.,
2
1
)(;,
2
1
2
2
2
2
∞<<∞−
π
=∞<<∞−
π
=
−−
yeyfxexf
yx
Знайти f (z), якщо
.
Х
Y
Z =
Розв’язання. Згідно з (214) маємо
()
() ()
(
)
(
)
.
)1(
1
1
1
1
1
.
2
1
1
1
1
1
2
1
2
1
2
1
2
1
2
1
2
0
2
2
2
1
2
0
2
2
2
1
2
2
2
2
0
2
2
2
2
0
zz
x
z
x
z
z
zxxzxx
zzz
e
z
e
z
dxxeedxxeezf
+π
=
⎥
⎦
⎤
⎢
⎣
⎡
+
+
+
π
=
+
+
⎢
⎣
⎡
+
−
π
=
=
ππ
−
ππ
=
∞−
+−
∞
+−
−−
∞−
−−
∞
∫∫
Перевірка умови нормування:
.1
22
11
)1(
1
1)(
0
=
⎟
⎠
⎞
⎜
⎝
⎛
π
+
π
π
=
π
=
+π
→=
∞
∞−∞−
∞
∞−
∫∫
Zdz
z
dxzf
z
arctg
Отже, f (z) знайдено правильно.
Таким чином,
()
)1(
1
2
z
zf
+π
=
,
.
∞
<
<
∞
−
z
4.3. Знаходження F(Z), f (z), якщо Z = ХY.
Якщо Z =ХY, тобто випадкова величина Z дорівнює добутку
двох випадкових величин Х і Y, то ймовірність потрапляння випад-
кової величини Z в область
zZD
<
:
(
)
zYX
<
унаочнює рис. 83.
XY < Z
0
x
y
Рис. 83
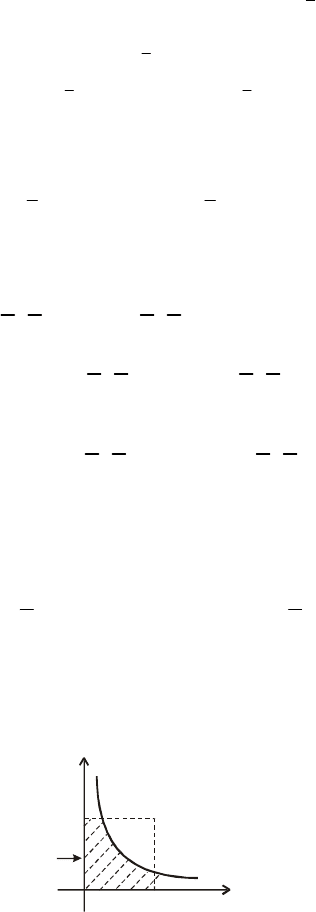
191
Маємо:
()
dxdyyxfdxdyyxfzFzZPzXYP
x
z
x
z
),(),()()(
0
0
∫∫∫∫
∞
∞−∞−
∞
+==<=<
або
∫∫∫∫
∞∞−∞−
∞
−==<
x
z
x
z
dxdyyxfdxdyyxfzFzZP
0
0
),(),()()(
. (215)
Скориставшись (215), дістанемо
()
.
11
,
1
,
)(
0
0
0
0
),(),(
dx
xx
xfdx
xx
z
xf
'
ZFzf
x
z
x
z
dxdyyxfdxdyyxf
x
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
=
==
′
=
∫∫
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
∫∫ ∫∫
−
∞−
∞
∞−
∞
∞∞−
Отже,
()
.
1
,
1
,
0
0
dx
xx
z
xfdx
xx
z
xfzf
∫∫
∞−
∞
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
=
(216)
Якщо випадкові величини Х і Y є незалежними, то
()
dx
xx
z
fxfdx
xx
z
fxfzf
1
)(
1
)(
0
0
∫∫
∞−
∞
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
=
. (217)
Приклад 7. Незалежні випадкові величини Х і Y мають
рівномірний закон розподілу ймовірностей, щільності ймо-
вірностей яких такі:
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<
≤
=
;2,0
;20,
2
1
;0,0
x
x
x
xf
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<
≤
=
.2,0
;20,
2
1
;0,0
y
y
y
yf
Знайти F (z), f (z), якщо Z = XY.
Розв’язання. Імовірність влучення випадкової величини Z = XY в
область D зображена на рис. 84.
0 2
x
y
2
D
Рис. 84
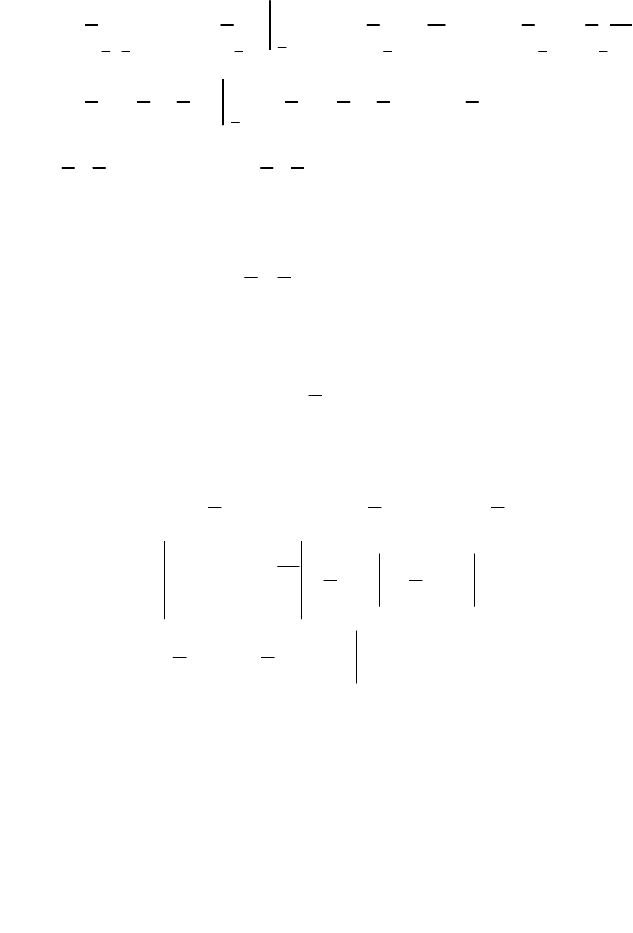
192
Згідно з (217) маємо:
()
).ln2ln2(
44
)2lnln2(ln
44
2
ln2ln
42
2
2
1
1ln
42
2
2
1
1
42
1
1)
Χ
Ζ
2(
4
1
1
4
1
1
4
1
1
2
2
2
2
2
22
2
22
z
zz
z
zz
zzz
x
zz
x
dxz
dxdxdxydxdyzF
x
z
zz
x
z
x
z
x
z
x
z
z
z
−+=+−+=
=
⎟
⎠
⎞
⎜
⎝
⎛
−+
⎟
⎠
⎞
⎜
⎝
⎛
−−=+
⎟
⎠
⎞
⎜
⎝
⎛
−−=
=+−=−−=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−=−=
∫∫∫∫∫∫
Отже,
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−+
≤
=
.4,1
;40),ln2ln2(
44
;0,0
z
zz
zz
z
zF
Звідси F (z) = F' (z) =
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−
≤
.4,0
;40),ln2ln2(
4
1
;0,0
z
zz
z
Перевірка виконання умови нормування:
.112ln22ln24ln4
4
1
42ln
2
1
ln
4
1
2ln
2
1
,
,ln
ln
4
1
2ln2
4
1
)ln2ln2(
4
1
1)(
4
0
4
0
4
0
4
0
4
0
4
0
4
0
4
0
=+−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−
⎟
⎠
⎞
⎜
⎝
⎛
=
=
⎥
⎦
⎤
⎢
⎣
⎡
−−=
==
==
=
=−==−→=
∫
∫∫∫∫
z
dzzzz
zvdvdz
z
dz
duuz
zdzdzdzzdzzf
Умова нормування виконується. Отже, f (z) знайдено вірно.
5. Числові характеристики функції
n випадкових аргументів
1. Математичне сподівання.
А. М (Х + Y) = М (Х) + М (Y). (218)
Доведення. Нехай Х і Y є неперервними випадковими величи-
нами. Тоді
!

193
()
∫∫
∫∫∫∫
∫∫ ∫∫
∫∫
∞
∞−
∞
∞−
∞
∞−
∞
∞−
∞
∞−
∞
∞−
∞
∞−
∞
∞−
∞
∞−
∞
∞−
∞
∞−
∞
∞−
+=+=
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
=
=+=
=+=+
).()()()(
),(),(
),(),(
),()(
YMXMdyyyfdxxxf
dydxyxfydxdyyxfx
dydxyxyfdydxyxxf
dydxyxfyxYXM
Оскільки
∫
∞
∞−
= )(),( xfdyyxf
, то
∫
∞
∞−
= ).(),( yfdxyxf
Висновок 1.
М (АХ + ВY + С) = АМ (Х) + ВМ (Y) + С. (219)
тут А, В, С — деякі сталі.
Доведення.
()
() ()
,)()(
),(),(),(
),(),(),(
),()(
CYBMXAMCyyfBxxfA
dydxyxfCdydxyxfyBdxdyyxfxA
dydxyxCfdydxyxByfdydxyxAxf
dydxyxfCByАxCBYAXM
++=++=
=+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
=++=
=++=++
∫∫
∫∫∫∫∫∫
∫∫ ∫∫ ∫∫
∫∫
∞
∞−
∞
∞−
∞
∞−
∞
∞−
∞
∞−
∞
∞−
∞
∞−
∞
∞−
∞
∞−
∞
∞−
∞
∞−
∞
∞−
∞
∞−
∞
∞−
∞
∞−
∞
∞−
оскільки
∫∫
∞
∞−
∞
∞−
= .1),( dydxyxf
Висновок 2.
∑∑
==
=
⎟
⎠
⎞
⎜
⎝
⎛
n
i
i
n
i
XMXM
11
)( . (220)
Б. Якщо випадкові величини є між собою незалежними, то
М (ХY) = М (Х) М (Y). (221)
Доведення.
() ()()
YMXMdydxyfxfxydydxyxfxyXYM
∫∫∫∫
∞
∞−
∞
∞−
∞
∞−
∞
∞−
=== )()(),(
(оскільки для незалежних випадкових величин f (x, y) = f (x) f (y)).
!
!

194
Висновок. Для n незалежних випадкових величин
).(
11
∏∏
==
=
⎟
⎠
⎞
⎜
⎝
⎛
n
i
i
n
i
i
ХМХM
(222)
В. Якщо випадкові величини Х і Y є залежними, то
М (ХY) = М (Х) М (Y) + K
ху
.
(223)
Формула (223) випливає з визначення кореляційного моменту
K
ху
= М (ХY) – М (Х) М (Y).
2. Дисперсія.
A. D (Х + Y) = D (Х) + D (Y) + 2K
ху
.
(224)
Доведення.
(
)( )
2
2
))()(()()( YМХМYХМYХМYХMYXD −−+=+−+=+ ;
(
)( )
()
()()
,2)()(
))())(((2))((
)(())((2))(())((
)()((
2
2
22
2
xy
KYDXD
YМYХМХМYМYМXMXM
ХМYХМХYМYХМХМ
YМYХМХM
++=
=−−+−+−=
=−−+−+−=
=−+−=
де K
ху
= М (Х – М (Х)) (Y – M (Y)).
Висновок 1.
D (АХ + ВY + С) = А
2
D (Х) + В
2
D (Y) + 2АВK
ху
.
(226)
Доведення.
()
(
)
(
)
(
)
() ()()
()()()()()
()
.2)()(
))())(((2))(())((
))())(((2))(())((
22
2222
2222
2
2
2
xy
АBKYDBХDA
YМYХМХАBМYМYМBХМХМA
YМYYМХАBYМYBХМХАM
YMYBXMXAM
CYBMXAMCBYAXM
CBYAXMCBYAXMCBYAXD
++=
=−−+−+−=
=−−+−+−=
=−+−=
=−−
−++=
=++−++=++
Висновок 2.
∑∑∑
===
+=
⎟
⎠
⎞
⎜
⎝
⎛
ij
j
i
n
j
j
n
i
i
KХDХD 2)(
11
. (227)
Якщо
,,1,,,0 njijiK
ij
=≠= то
).(
11
∑∑
==
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
n
j
i
n
j
j
ХDХD (228)
!
!

195
Б. Якщо випадкові величини є незалежними, то
D (ХY) = D (Х) D (Y) + М
2
(Х) D (Y) + М
2
(Y) D (Y), (229)
або
D (ХY) = (D (Х) + М
2
(Х)) (D (Y) + М
2
(Y)) – М
2
(Х) М
2
(Y).
Доведення.
(
)
(
)()
(
)
()
()
()
()
),()()()())(()(
)()()(
)()()()(2)(
)()()()(2
)()(2
2222
2222
222222
2222
222
2
YМХМYМYDХМХD
YМХМYМXM
YМХМYМХМYМXM
YМХМYМХМХYYХM
YХМYХМYХYXMXYMXYMXYD
−++=
=−=
=+−=
=+−=
=+−=−=
оскільки
(
)
),()(
22
ХМХDXM +=
(
)
)()(
22
YМYDYM += .
Висновок. Для n незалежних випадкових величин маємо:
()
)()()(
1
2
1
2
1
i
n
j
n
j
ii
n
j
j
ХМХМХDХD
∏∏∏
===
−+=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
(230)
Приклад 8. Відомі значення: М (Х) = – 2; D (Х) = 4; М(Y) = – 3;
K
ху
= – 1.
Знайти М (Z), D (Z), σ (Z), якщо Z = – 9х + 5у + 3.
Розв’язання. Скориставшись (219) і (226) дістанемо:
М (Z) = М (– 9х + 5у + 3 ) = – 9 М (X) + 5 М (Y) + 3 =
= – 9 (– 2) + 5 (– 3) + 3 = 18 – 15 + 3 = 6.
D (Z) = D (– 9х + 5у + 3) = 81 D (X) + 25D (Y) + 2 (– 9 ) 5 K
ху
=
= 81D (X) + 25 D (Y) – 90 K
ху
= 81· 4 + 25 · 3 – 90 (– 1) =
= 324 + 75 + 90 = 489.
()
.1,22489)( ≈==σ zDz
Приклад 9. За заданою щільністю ймовірностей
()
∞<<∞−
π
=
−
xexf
x
,
2
1
2
2
знайти М (Y); Kху, якщо Y = 3х
2
– 2х
2
+ х +1.
Розв’язання. Для знаходження М (Y), K
ху
, необхідно визначити
),(),(),(,)(
234
ХМХМХМXM
оскільки:
()
()
(
)
1)()(23123
2323
++−=++−= xМxМxMxxxMYM ;
K
ху
= М (XY) – М (Y) М (X),
!
196
де
()
()
(
)
=++−=++−= xxxxMxxxxМxyM
23423
23)123(
).()()(2)(3
234
xМxМxМxМ ++−=
()
;0
2
1
)(
2
2
=
π
==
∫∫
∞
∞−
−
∞
∞−
dxxedxxxfXM
x
М (Х) = 0;
()
.1
2
2
2
2
2
2
,
2
2
2
1
)(
0
2
2
0
2
2
2
2
2
2
2
2
2
2
2
222
=
π
π
=
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+−
π
=
−=υ→υ=
==
=
=
π
=
π
==
∫
∫∫∫
∞
−
∞
−
−−
−
∞
∞−
−
∞
∞−
∞
∞−
dxexe
eddxxe
dxduxu
dxexdxexdxxfxXM
xx
xx
xx
М (х
2
) = 1;
()
;0
2
1
)(
2
2
333
=
π
==
−
∞
∞−
∞
∞−
∫∫
dxexdxxfxxM
x
М (х
3
) = 0;
()
.3
2
2
2
6
2
6
2
6
,
2
6
2
2
2
2
3,
2
1
)(
0
2
2
0
2
2
0
2
2
2
2
2
2
2
2
0
2
2
2
0
2
0
2
2
3
2
2
0
4
2
2
2
2
23
2
2
444
=
π
π
=
π
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+−
π
=
=
−=υ→υ=
==
=
π
=
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+−
π
=
π
=
=
−=υ
→υ=
==
=
π
==
∫∫
∫
∫∫
∫∫
∞
−
∞
−
∞
−
−−
−
∞
−
∞
∞
−−
∞
−
−−
∞
∞−
∞
∞−
dxedxexe
eddxxe
dxdxxu
dxex
dxexexdxex
e
ddxxe
dxxduxu
dxexdxxfxxM
xxx
xx
x
xxx
x
xx
()
;3
4
=xM
()
()
;11012031)()(23
23
−=++⋅−⋅=++−= xМxМxMYM
()
()
;8010233)()()(23
234
=++⋅−⋅=++−= xМxМxМxMXYM
() ()
.80)1(8)(
=
−
−
=
−
=
XМYMXYMK
xy
197
Приклад 9. Задано щільності ймовірностей незалежних ви-
падкових величин Х і Y:
()
⎩
⎨
⎧
>
≤
=
−
;0,2
;0,0
2
xe
x
xf
x
f (у) =
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−
−≤
=
.4,0
;42,
6
1
;2,0
y
y
y
yf
Знайти М (Z), D (Z), якщо виконуються умови:
1) Z = 3х – 5у + 1; 2) Z = ХY; 3) Z = –2х – 3у + 1.
Розв’язання. Обчислимо: М (Х); М (Х
2
), М(Y); М (Y
2
).
()
;
2
1
2
1
2
,,
2)(
0
2
0
2
0
2
0
2
22
00
2
=−==+−=
=
−=υ→υ=
==
===
∞
−
∞
−
∞
−
∞
−
−−
∞∞
−
∫∫
∫∫
xxxx
xx
x
edxedxexe
eddxe
dxduxu
dxexdxxxfXM
()
.
2
1
=XM
()
;
2
1
2
1
2
,
22
2
2,
2)(
0
2
0
2
0
2
0
2
2
2
0
2
0
2
0
22
2
2
2
2
00
222
=−==+−=
=
−=υ→
→υ=
==
==+−=
=
−=υ→
→υ=
==
===
∞
−
∞
−
∞
−
∞
−
−
−
∞
−
∞
−
∞
−
−
−−
∞∞
∫∫
∫∫
∫∫
xxxx
x
xxxx
x
xx
edxedxexe
e
ddxe
dxduxu
dxexdxexex
e
ddxe
xdxduux
dxexdxxfxXM
()
;
2
1
2
=XM
()
()
;
4
1
4
1
2
1
2
1
2
1
)(
2
22
=−=
⎟
⎠
⎞
⎜
⎝
⎛
−=−= xМxMXD
()
;
4
1
=XD
()
;1
12
416
126
1
)(
4
2
2
4
2
4
2
=
−
====
−
−−
∫∫
y
dyydyyyfYM
М (Y) = 1;
()
()
;4
18
72
18
864
186
1
2
4
3
4
2
4
2
222
==
+
====
−
−−
∫∫
y
dyydyyfyYM
М (Y
2
) = 4;
198
()
(
)
.314)(
22
=−=−= YМYMYD
(
)( )
(
)
(
)
:5,2
2
5
2
83
4
2
3
15
2
3
115
2
1
3
153153.1
−=−=
−
=−=+−=+⋅−=
=
+
−
=
+−= yMxMyxMZM
М (Z) = – 2,5;
() ( )
(
)
(
)
;29,77
4
309
75
4
9
325
4
1
9
259153
==+=⋅+=
=
+
=
+−
=
yDxDyxDZD
D (Z) = 77,29.
() ( )
;
2
1
1
2
1
)()(.2 ==== yМxМxyMZM
М (Z) = 0,5.
() ( )
(
)
(
)
()
;75,1
4
7
4
1
21
4
1
13
4
1
4
1
)()()()()()(
2222
==−=−+
⎟
⎠
⎞
⎜
⎝
⎛
+=
=−++== yМxМyМyDxМxDxyDZD
D (Z) = 1,75.
(
)( )
(
)
(
)
;3131113
2
1
2
132132.3
−=+−−=+⋅−−=
=
+
−
−
=
+
−−= yMxMyxMZM
М (Z) = – 3.
() ( ) () ()
2827139
4
1
494132 =+=⋅+=+=+−−= yDxDxxDZD
;
D (Z) = 28.
Приклад 10. Двовимірна випадкова величина (Х, Y) має та-
кий закон розподілу ймовірностей
Y
X
5 10 15 20 р
yi
– 6 0,02 0,01 0,03 0,04 0,1
– 4 0,18 0,09 0,07 0,06 0,4
– 2 0,1 0,2 0,1 0,1 0,5
р
xj
0,3 0,3 0,2 0,2
Знайти М (Z), D (Z), якщо:
1) Z = – 4х – 3у + 10; 2) Z = 3х – 9у – 7.
Розв’язання. Обчислимо М (Х); D (Y), D (Y); K
ху
.
