Жлуктенко В. І., Наконечний С. І. Теорія ймовірностей і математична статистика: У 2 ч. - Ч. І. Теорія ймовірностей
Подождите немного. Документ загружается.

199
()
.5,114335,12,0202,0153,0103,05р
4
1
=+++=⋅+⋅+⋅+⋅==
∑
=j
xjj
xXM
М (Х) = 11,5.
()
.5,1628045305,7
2,04002,02253,01003,025
4
1
22
=+++=
=⋅+⋅+⋅+⋅==
∑
=
xj
j
j
xXM р
()
(
)
.25,3025,1325,162)5,11(5,162)(
222
=−=−=−= XМXMXD
D (Х) = 30,25.
()
.2,316,16,05,024,041,06
3
1
−=−−−=⋅−⋅−⋅−==
∑
=
yi
i
i
yYM р
()
.1224,66,35,044,0161,036
3
1
22
=++=⋅+⋅+⋅==
∑
=
yi
i
j
yYM р
()
(
)
.76,124,1012)2,3(12)(
222
=−=−−=−= YМYMYD
D (Y) = 1,76.
()
.9,3643418,4
2,46,36,38,47,26,06,01,02021,01522,0102
1,05206,020407,015409,010418,05404,0206
03,015601,010602,056
3
1
4
1
−=−−−−−
−−−−−−−−=⋅⋅−⋅⋅−⋅⋅−
−⋅⋅−⋅⋅−⋅⋅−⋅⋅−=⋅⋅−⋅⋅−
−⋅⋅−⋅⋅−⋅⋅−==
∑∑
==
ij
ij
ji
xyXYM р
М (ХY) = – 36,9.
() ()
;1,08,369,36)2,3(5,119,36)( −
=
+
−
=
−
−
−
=
−
=
YМXMXYMK
xy
K
ху
= – 0,1.
(
)( )
(
)
(
)
.4,26106,94610)2,3(35,114
10341034)1
−=++−=+−⋅−⋅−=
=
+
−
−
=
+
−−= yMxMyxMZM
М (Z) = – 26,4.
() ( )
(
)
(
)
(
)
(
)
.44,4974,284,15484)1,0(12276,1925,3016
3429161034
=−+=−⋅+⋅+⋅=
=
−
−
+
+
=
+−−
=
xy
KyDxDyxDZD
D (Z) = 497,44.
(
)
(
)
(
)
.3,5678,285,347)2,3(95,113
793)793()2
=−+=−−−⋅=
=
−
−
=
−
−= YMXMyxMZM
М( Z) = 56,3.
() ( )
(
)
(
)
(
)
(
)
.21,4204,556,14225,2721,05476,18125,309
932819793
=++=⋅+⋅+⋅=
=−++=−−=
xy
KYDXDyxDZD
D (Z) = 420,21.
200
Приклад 11. Відомо, що 5432
321
+
−
−
=
xxxX . Знайти
М (Х), D (Х), коли М (Х
1
) = – 2, М (Х
2
) = 3, М (Х
3
) =1; D (X
1
) = 4;
D (X
2
) = 3; D (X
3
) = 5; r
12
= 0,36; r
13
= 0,3; r
23
= – 0,1.
Розв’язання. Використовуючи властивості математичного споді-
вання, дисперсії та парного коефіцієнта кореляції, одержимо:
M(x) = M(2x
1
– 3x
2
– 4x
3
+ 5) = 2M(x
1
) – 3M(x
2
) + 4M(x
3
) + 5 =
= 2 (–2) – 3 · 3 + 4 · 1 + 5 = – 4 – 9 + 4 + 5 = – 4.
M(x) = 4.
D (x) = D (2x
1
– 3x
2
– 4x
3
+ 5) = 4D (x
1
) + 9D (x
2
) + 16D (x
3
) +
+ 2(2) (– 3)K
12
+ 2 (2) (– 4)K
13
+ 2 (– 3) (– 4)K
23
=
= 4D (x
1
) + 9D (x
2
) + 16D (x
3
) – 12 K
12
– 16 K
13
+ 24 K
23
.
Оскільки
)()(
21
12
12
xx
K
r
σσ
=
;
)()(
21
13
13
xx
K
r
σσ
=
;
)()(
32
23
23
xx
K
r
σσ
=
, то:
()()
;24704,1732,1236,03436,0
)()(36,0
21211212
=⋅⋅==
==σσ= xDxDxxrK
()()
;3418,1236,223,0
543,0)()(
2113211313
=⋅⋅=
===σσ= xDxDrxxrK
()()
.397,0236,2732,111,0
531,0)()(1,0
32322323
−=⋅⋅⋅−=
=−=−=σσ= xDxDxxrK
Отже,
D (x) = 4 · 4 + 9 · 3 + 16 · 5 – 12 · 1,24704 – 16 · 1,3418 + 24 (– 0,397) =
= 16 + 27 + 80 – 14,965 – 21,469 – 9,528 = 77,038.
D (x) = 77,038.
Приклад 12. За заданою кореляційною матрицею
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
−
−
=
4
4,025
8,019
5,02,01,016
K
знайти D (X), якщо Х = 4х
1
– 3х
2
– 5х
3
– х
4
+ 5.
Розв’язання. Використовуючи властивості дисперсії, дістаємо:
D (x) = D (4х
1
– 3х
2
– 5х
3
– х
4
+ 5) = 16D (х
1
) + 9D (х
2
) + 25D (х
3
) +
+ D (х
4
) + 2 · 4(–3)K
12
+ 2 · 4 (–5)K
13
+ 2 · 4 (–1)K
14
+ 2 (–3) (–5)K
23
+
+ 2(–3)(–1)K
24
+ 2(–5)(–1)K
34
= 16D (х
1
) + 9D (х
2
) + 25D (х
3
) +
+ D (х
4
) – 24K
12
– 40K
13
– 8K
14
+ 30K
23
+ 6K
24
+ 10K
34
= 16 · 16 + 9 · 9 +
201
+ 25 · 25 + 4 – 24 · 0,1 – 40 · 0,2 – 8 · 0,5 + 30 · 1 + 6 (– 0,8) + 10 (– 0,4) =
= 256 + 81 + 625 + 4 – 2,4 – 8 – 4 +30 – 4,8 – 4 = 972,8.
D (x) = 972,8.
Приклад 13. За заданою кореляційною матрицею
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
=
16
04
001
0009
K
знайти D (X), якщо Х = –3х
1
– 2х
2
– х
3
– 5х
4
+ 100.
Розв’язання. Використовуючи властивості дисперсії, одержимо:
() ( )
.4894004481162541499
)(25)()(4)(9
100523
4321
4321
=+++=⋅++⋅+⋅=
=+++=
=
+
−
−
−−
=
xDxDxDxD
xxxxDXD
D (Х) = 489.
Приклад 14. Нехай
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−
−≤
=
.1,0
;11,
2
3
;1,0
2
x
xx
x
xf
Знайти f (у), якщо Y = min (Х; 1).
Розв’язання. Випадкова величина Y буде величиною мішаного виду:
при
U
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−−∈ 1;
3
2
3
2
;1Y
Y = 1;
при
U
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−∈
3
2
;00;
3
2
Y
Y = Х.
Графік f (у) зображено на рис. 85.
3
2
–
3
2
f
y
()
y
3
2
–
3
2
Pис. 85
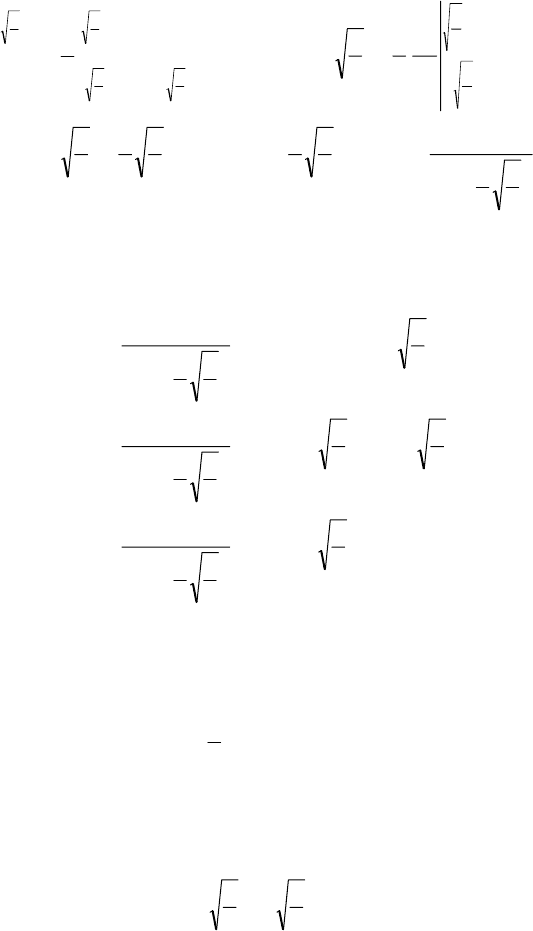
202
Для f (y) на проміжку
[
]
1;1
−
має виконуватися умова нормування:
.
3
2
3
2
12
1
1
3
2
3
2
121
3
2
3
2
3
2
12
1
32
3
3
2
121
2
3
3
2
3
2
3
3
2
1
3
2
3
2
1
3
2
2
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=→=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−→=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−→
→=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−→=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
++
−
∫∫∫
−
−
−
aaa
y
adydyydya
Отже,
()
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎧
>
≤<
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−≤<−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−≤<−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−≤
=
.1,0
;1
3
2
,
3
2
3
2
12
1
;
3
2
3
2
,
3
2
3
2
14
3
;
3
2
1,
3
2
3
2
12
1
;1,
0
2
y
y
yy
y
y
yf
Приклад 15. Задано
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−
−≤
=
.1,0
;11,
2
3
;1,0
2
x
xx
x
xf
Знайти f (у), якщо Y = max (Х; 1).
Розв’язання. Випадкова величина Y буде величиною мішаного виду:
при
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−−∈ 1;
3
2
3
2
;1
UY Y = Х;
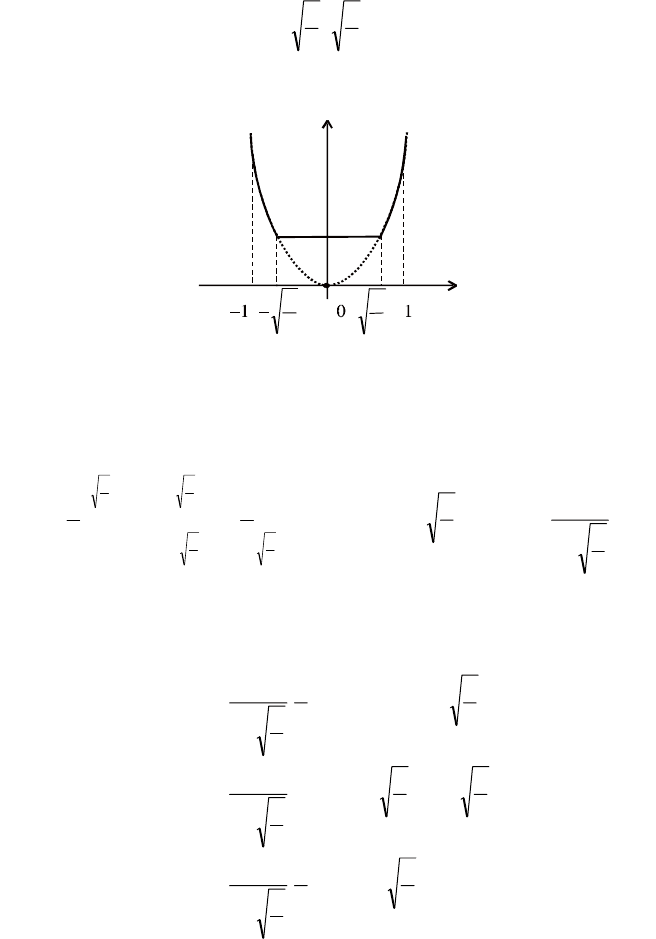
203
при
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−∈
3
2
;
3
2
Y
Y = 1.
Графік f (у) зображено на рис. 86.
3
2
3
2
y
3
2
3
2
f
y
()
Рис. 86
За умовою нормування для випадкової величини Y на проміжку
[]
1;1− дістаємо:
.
3
2
1
1
1
3
2
11
2
3
2
3
3
2
1
3
2
3
2
1
3
2
22
−
=→=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−→=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
++
∫∫∫
−
−
−
aadyydydyya
Отже,
()
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎧
>
≤<
−
≤<−
−
−≤<−
−
−≤
=
.1,0
;1
3
2
,
2
3
3
2
1
1
;
3
2
3
2
,
3
2
1
1
;
3
2
1,
2
3
3
2
1
1
;1,0
2
2
y
yy
y
yy
y
yf

204
Теоретичні запитання до теми
?
1. Як обчислити щільність імовірностей випадкової вели-
чини Y, якщо Y = α(Х), де α(х) — монотонна функція, і ві-
домий закон розподілу випадкової величини Х?
2. Як обчислити f (у), якщо Y = α(х), де α(х) — немонотонна
функція, і відомий закон розподілу випадкової величини Х?
3. Числові характеристики функції дискретного випадково-
го аргументу.
4. Числові характеристики функції неперервного випадко-
вого аргументу.
5. Як визначити F(Z), f (z), якщо Z = Х + Y ?
6. Як визначити F(Z), f (z), якщо
Х
Y
Z =
?
7. Як визначити F(Z), f (z), якщо Z = Х Y ?
8. Що означає здійснити композицію двох законів розподілу?
9. Довести, що М (Х + Y) = … .
10. Довести, що М (АХ + ВY + С ) = … , якщо А, В, С — де-
які сталі.
11. Довести, що М (ХY) = … .
12. Довести, що D (Х + Y) = … .
13. Довести, що D (АХ + ВY + С) = … , якщо А, В, С — деякі
сталі.
14. За якої умови М (Х Y) = М (Х) М (Y)?
15. Довести, що D (Х Y) = … .
16. Чому дорівнює ?...
1
=
⎟
⎠
⎞
⎜
⎝
⎛
∑
=
n
i
i
xM
17. Чому дорівнює
?...
1
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∑
=
n
j
j
xD
18. За якої умови ?)(
1µ
µ
1µ
µ
∏∏
==
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
nn
xМxM
19. Чому дорівнює
?...
1
=
⎟
⎠
⎞
⎜
⎝
⎛
∏
=
n
i
i
xD
20. Чому дорівнює дисперсія від суми n некорельованих ви-
падкових величин?
21. Чому дорівнює коефіцієнт кореляції випадкових вели-
чин Y і Х, якщо між ними існує лінійна функціональна за-
лежність ?
22. Довести, що
yxxy
K σσ≤
.
23. Довести, що .1≤
xy
r
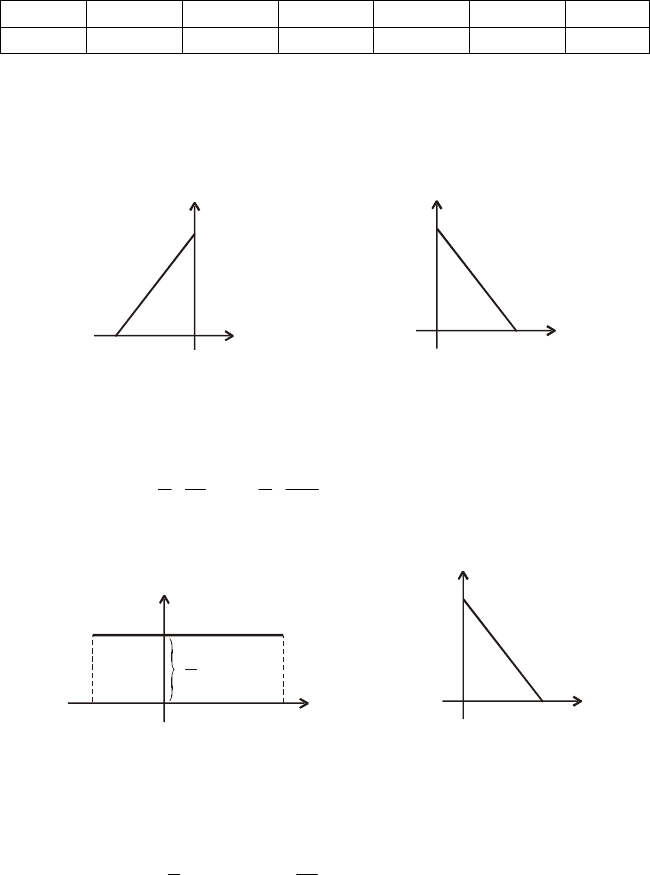
205
Приклади до теми
1. Задано
x
i
0,001 0,01 0,1 10 100 100
p
i
0,1 0,2 0,2 0,2 0,1 0,2
Обчислити М (Y), D (Y), σ (Y), якщо Y = lg х.
Відповідь. М (Y) = 0, D (Y) = 3,8; σ (Y)
≈
1,95.
2. Незалежні випадкові величини Х і Y мають щільності ймовір-
ностей згідно з pис. 87 і 88.
fx
()
–
2 0
х
f
y
()
0 2
y
Рис. 87 Рис. 88
Визначити: 1) М (2х + 3у – 2 ); D (2х + 3у – 2);
2) М (Х Y); D (ХY).
Відповідь. 1)
.
324
57
;
9
4
)2;
6
13
;
3
4
−
3. Випадкові величини Х і Y є залежними і мають щільності ймо-
вірностей згідно з рис. 89 і 90.
8
1
fx
()
–
3 0 5
x
8
1
f
y
()
0 2
y
Рис. 89 Рис. 90
Знайти: 1) М (4х – 5у – 1 ); D (4х – 5у – 1);
2) М (–4х – 10у + 5 ); D (– 4х – 10у + 5);
3) М (ХY). При цьому відоме значення K
xy
= – 0,5.
Відповідь.
;5,70;
3
1
)1 − ;56,67;
3
17
)2 − 3) 0,193.

206
4. Задано
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
<<
≤
=
.2,0
;20,
2
1
;0,0
x
x
x
xf
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−
−≤
=
.1,0
;11,
2
1
;1,0
y
y
y
yf
Знайти f (Z), якщо Z = Х + Y.
Відповідь.
()
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎨
⎧
>
≤<
−
≤<−
+
−≤
=
.3,0
;31,
4
3
;11,
4
1
;1,0
z
z
z
z
z
z
zf
5. Задані закони розподілу двох незалежних випадкових величин
Х і Y є щільностями ймовірностей:
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−
−≤
=
.2,0
;22,
4
1
;2,0
x
x
x
xf
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−
−≤
=
.6,0
;62,
8
1
;2,0
y
y
y
yf
Знайти F (z), f (z), якщо Z = Х +Y.
Відповідь.
()
()
()
⎪
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎧
>
≤<
−
−
≤<
+
≤<−
+
−≤
=
.8,1
;84,
64
8
1
;49,
8
4
;04,
64
4
;4,0
2
2
z
z
Z
z
Z
z
Z
z
zF
()
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎨
⎧
>
≤<
−
−
≤<
≤<−
+
−≤
=
.8,0
;84,
32
8
;40,
8
1
;04,
32
4
;4,0
z
z
Z
z
z
Z
z
zf
6. Двовимірна випадкова величина (Х і Y) має закон розподілу
ймовірностей:

207
Y
Х
4 6 8 Ру
і
10 0,03 0,07 0,2 0,3
20 0,27 0,23 0,2 0,7
Рх
j
0,3 0,3 0,4
Знайти М (Z), D (Z), якщо виконуються умови:
1) Z = – 9х + 2у –5;
2) Z = –3х – 2у +5;
3) Z = ХY.
Відповідь. 1) –26,8; 408,36; 2) – 47,6; 75,24; 3) 96,6.
7. Відомі значення випадкового вектора (Х, Y):
М (Х) = –1; М (Y) = 4; D (Х) = 2; D (Y) = 5;
r
ху
= – 0,4.
Знайти М (Z), D (Z), якщо: 1) Z = –х – 5у + 5;
2) Z = 2х – 9у – 3;
3) Z = ХY.
Відповідь. 1) –14; 114,36; 2) –37; 367,96; 3) –2,736.
8. За заданою кореляційною матрицею
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
=
16
19
5,08,01
14,08,04
K
знайти D (Х), якщо:
1) Х = 2х
1
– 3х
2
– 4х
3
– х
4
+ 2;
2) Х = –3х
1
– 5х
2
+ х
3
– 6х
4
–1.
Відповідь. 1) 216,4; 2) 650,6.
9. За заданою кореляційною матрицею
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
=
25
04
009
0001
K
знайти D (Z), якщо: 1) Z = – 4х
1
+х
2
– 5х
3
– х
4
+ 5;
2) Z = 5х
1
– 2х
2
– 3х
3
– 4х
4
– 100.
Відповідь. 1) 150; 2) 497.

208
10. Незалежні випадкові величини Х і Y мають рівномірний закон
розподілу, щільності ймовірностей яких відповідно такі
()
⎪
⎩
⎪
⎨
⎧
>
≤<
≤
=
.1,0
;10,1
;0,0
x
x
x
xf
()
⎪
⎩
⎪
⎨
⎧
>
≤<
≤
=
.1,0
;10,1
;0,0
y
y
y
yf
Знайти f (z), якщо Z = XY. Чому дорівнюють M (Z), D (Z)?
Відповідь.
()
⎪
⎩
⎪
⎨
⎧
>
≤<−
≤
=
.1,0
10,ln
0,0
z
zz
z
zf
M (Z) = 0,25;
()
144
7
=ZD
.
11. Знайти f (z), якщо
Х
Y
Z =
, де Х і Y є незалежними випадкови-
ми величиними, закони яких задані щільностями ймовірностей:
()
⎩
⎨
⎧
>
≤
=
−
;0,6
,0,0
6
xe
x
xf
x
()
∞<<∞−
π
=
−
yeyf
y
,
2
1
2
2
.
Відповідь.
()
⎪
⎩
⎪
⎨
⎧
>
≤
=
−
.0,
,0,0
2
18
zze
z
zf
z
12. Незалежні випадкові величини Х і Y мають такі щільності
ймовірностей:
()
⎩
⎨
⎧
>
≤
=
β−α
;0,
,0,0
1
xexC
x
xf
x
()
⎪
⎩
⎪
⎨
⎧
>
≤
=
β−γ
.0,
,0,0
2
yeyC
y
yf
y
Знайти С
1
, С
2
і f (z), якщо Z = Х + Y.
