Жлуктенко В. І., Наконечний С. І. Теорія ймовірностей і математична статистика: У 2 ч. - Ч. І. Теорія ймовірностей
Подождите немного. Документ загружается.

229
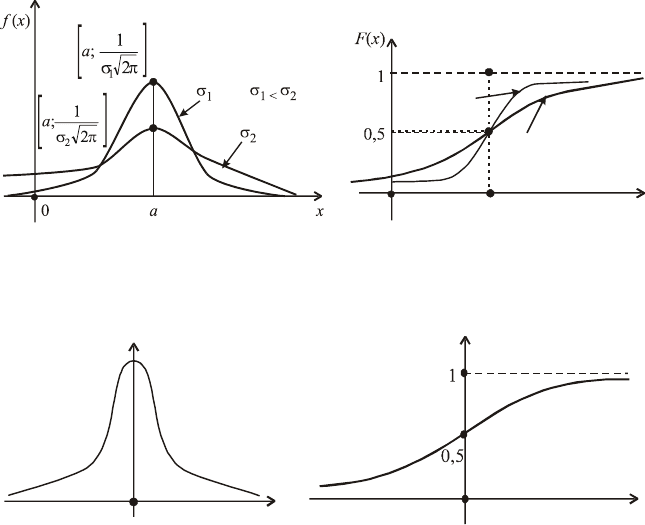
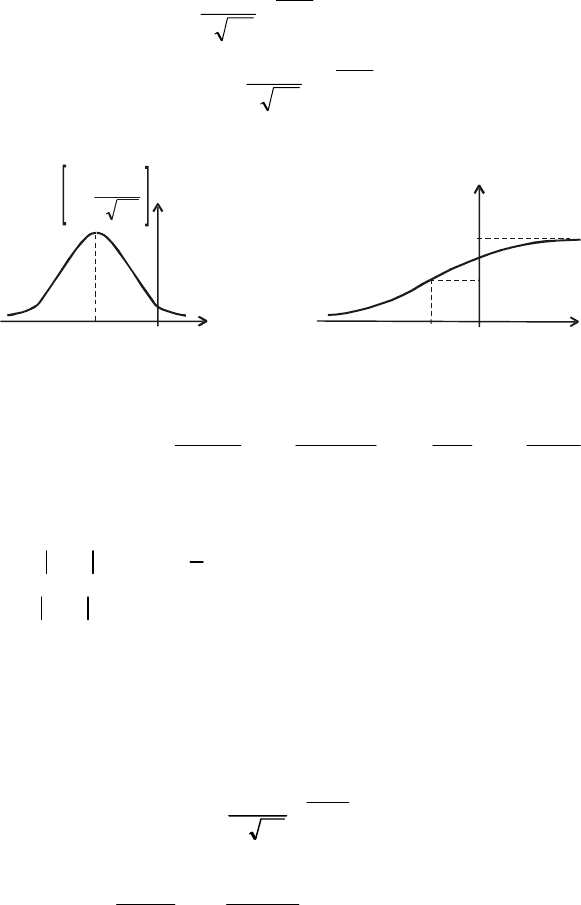
Із рис. 91 бачимо, що графік f (x) розміщений симетрично віднос-
но умовно проведеного перпендикуляра в точку Х = а. Зі зміною зна-
чень параметра а крива f (x) зміщується праворуч, якщо а > 0 або лі-
воруч, якщо a < 0, не змінюючи при цьому своєї форми; f (a) = max,
отже, Мо = а.
Із рис
. 92 бачимо, що графік F(x) є неспадною функцією, оскіль-
ки f (x) = F
′(x) > 0 і, як буде доведено далі, F(a) = 0,5.
Отже, Ме = а.
Зі зміною значень параметра а крива F(x) зміщується праворуч для
а > 0 або ліворуч при а < 0, не змінюючи при цьому форми кривої.
Отже, для нормального закону Мо = Ме = а.
Зі зміною значень
σ при а = const змінюється крутизна кривих у
околі значень X = а, що унаочнюють рис. 93 і 94.
0
a х
σ
1
σ
2
Рис. 93 Рис. 94
Для нормованого нормального закону графіки функцій f (x), F (x)
зображено на рис. 95 і 96.
0
x
f
x
()
0
х
Fx
()
Рис. 95 Рис. 96
Загальний нормальний закон позначають: N (a; σ). Так, наприк-
лад, N (–2; 4) — загальний нормальний закон із значенням парамет-
рів а = –2,
σ = 4.
Нормований нормальний закон позначають N (0; 1).
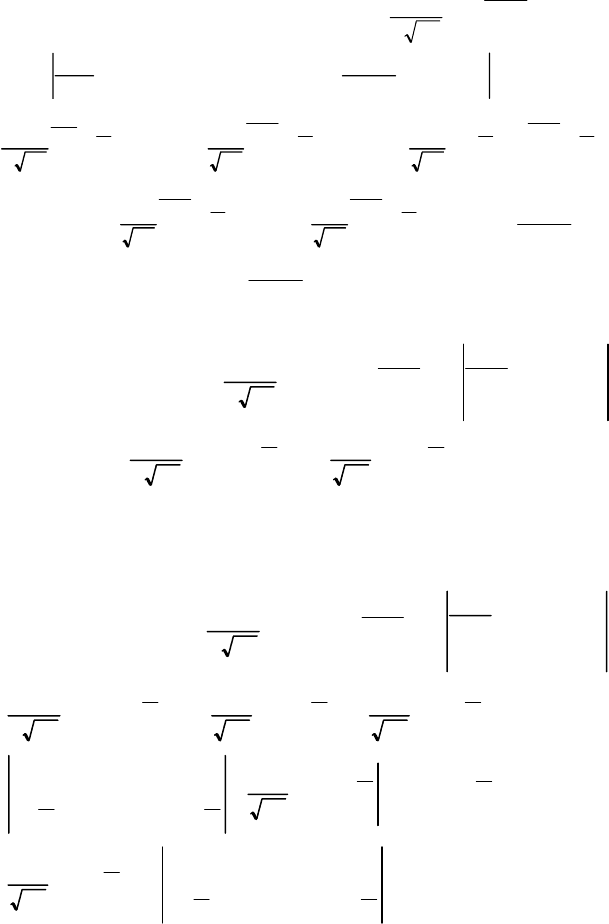
230
1.1. Визначення Ме, Аs, Es
По визначенню медіани маємо F(Me)=
∫
∞−
σ
−
−
πσ
Me
ax
е
2
2
2
)(
2
1
dx = 0,5 ⇒
.Me0
Me
0
Me
0
2
1
5,0
2
1
5,05,0
2
1
5,0
2
1
5,0
2
1
)Me(
Me
,Me
Me
0
2
Me
0
2
Me
0
2
0
2
Me
22
22
222
Me
2
a
a
a
dzedze
dzedzedzedze
Fdzdx
a
zxz
ax
a
z
a
z
a
zz
a
zz
a
=⇒=
σ
−
⇒=
=
⎟
⎠
⎞
⎜
⎝
⎛
σ
−
Φ⇒=
π
⇒=
π
+⇒=
=+
π
⇒=σ
π
⇒=σ
πσ
=
=⇒σ=→
σ
−
<<∞−<<∞−→=
σ
−
⇒
∫∫
∫∫∫∫
σ
−
−
σ
−
−
σ
−
−
∞−
−
σ
−
∞−
−
∞−
−
σ
−
Для визначення As необхідно знайти
µ
3
.
=
σ=−
==
σ
−
=−
πσ
=−=µ
σ
−
−
∞
∞−
∞
∞−
∫∫
zax
dzdxz
ax
dxeaxdxxfxMx
ax
,
)(
2
1
)())((
2
2
2
)(
33
3
0
22
1
2
3
3
2
33
22
=
π
σ
=σσ
πσ
=
∫∫
∞
∞−
−−
∞
∞−
dzezdzez
zz
,
оскільки підінтегральна функція є непарною, а межі інтегрування є
симетричними відносно нуля. Таким чином,
3
µ
= 0, а отже, і As = 0.
Для визначення Еs необхідно знайти
µ
4
.
=
−=→=
==
=
π
σ
=
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+−
π
σ
=
−=→=
==
=
=
π
σ
=
π
σ
=σσ
πσ
=
=
σ=−
σ==
σ
−
=−
πσ
=−=µ
−−
∞
−
∞
−
∞
−
−−
−
∞
−
∞
∞−
−
∞
∞−
σ
−
−
∞
∞−
∞
∞−
∫
∫
∫∫∫
∫∫
22
0
2
2
4
0
2
2
0
2
3
4
22
23
2
0
4
4
2
4
4
2
44
2
)(
44
4
22
2
22
22
222
2
2
;
2
6
3
2
2
3;
2
2
22
1
,
)(
2
1
)())((
zz
z
zz
zz
zzz
ax
evdvdzze
dzduzu
dzez
dzezez
evdvdzze
dzzduzu
dzezdzezdzez
zax
dzdxz
ax
dxeaxxfxMx
231
.3
2
2
2
6
2
6
2
6
4
4
0
2
4
0
2
0
2
4
222
σ=
π
π
σ
=
π
σ
=
⎥
⎥
⎦
⎤
+
⎢
⎢
⎣
⎡
−
π
σ
=
∫∫
∞
−
∞
−
∞
−
dzedzeze
zzz
Отже,
4
µ
=3
4
σ
.
Тоді Еs =
.03
3
3
4
4
4
4
=−
σ
σ
=−
σ
µ
Отже, доведено, що для нормального закону Аs = Es = 0 при
будь-яких обмежених значеннях параметрів а і
σ.
1.2. Формули для обчислення ймовірностей
подій:
.axx δβ;α <−<<
1)
()
∫∫
β
α
σ
−
−
β
α
=
πσ
==β<<α
dxedxxfxР
ax
2
2
2
)(
2
1
)(
.ФФ
2
1
2
1
2
1
2
1
2
1
2
1
,
00
22
0
0
222
2
22
222
2
⎟
⎠
⎞
⎜
⎝
⎛
σ
−α
−
⎟
⎠
⎞
⎜
⎝
⎛
σ
−β
=
π
−
π
=
=
π
+
π
=
π
=
=σ
πσ
=
σ
−β
<<
σ
−α
→β<<α
σ=+σ=→=
σ
−
=
∫∫
∫∫∫
∫
σ
−β
σ
−α
−−
σ
−α
σ
−β
−−
σ
−β
σ
−α
−
σ
−β
σ
−α
−
а
а
dzedze
dzedzedze
dze
a
z
a
x
dzdxazxz
ax
aa
zz
a
a
zz
a
a
z
a
a
z
Отже,
P(
β
<
<α x
) =
⎟
⎠
⎞
⎜
⎝
⎛
σ
−α
Φ−
⎟
⎠
⎞
⎜
⎝
⎛
σ
−β
Φ
аa
. (261)
2)
=δ+=βδ−=α=δ+<<δ−=δ<− aaaxaPaxP ,)()(
.2
⎟
⎠
⎞
⎜
⎝
⎛
σ
δ
Φ=
⎟
⎠
⎞
⎜
⎝
⎛
σ
δ
Φ+
⎟
⎠
⎞
⎜
⎝
⎛
σ
δ
Φ=
⎟
⎠
⎞
⎜
⎝
⎛
σ
δ
−Φ−
⎟
⎠
⎞
⎜
⎝
⎛
σ
δ
Φ=
⎟
⎠
⎞
⎜
⎝
⎛
σ
−δ−
Φ−
⎟
⎠
⎞
⎜
⎝
⎛
σ
−δ+
Φ=
aaaa
Отже,
()
⎟
⎠
⎞
⎜
⎝
⎛
σ
δ
Φ=δ<− 2axP
. (262)
232
Для N (0, 1) формули (261), (262) наберуть такого вигляду:
()
).(2
);()()(
δΦ=δ<
α
Φ
−
β
Φ
=
β
<
<
α
xР
xP
1.3. Правило трьох сигм
для нормального закону
Коли
σ=δ 3 , то згідно з (262) маємо:
()
9973,049865,02)3(2
3
23 =⋅=Φ=
⎟
⎠
⎞
⎜
⎝
⎛
σ
σ
Φ=σ<− axP .
Практично ця подія при одному експерименті здійсниться, а то-
му її вважають практично вірогідною. Звідси:
()
(
)
.0027,09973,01313 =−=σ<−−=σ>− axPaxP
Тобто ймовірність того, що внаслідок проведення експерименту
випадкова величина Х, яка має закон розподілу N (a;
σ), не потра-
пить у проміжок
[]
σ
+
σ
−
3;3 aa , дорівнює 0,0027. Це становить
0,27%, тобто практично вважається, що ця подія внаслідок прове-
дення одного експерименту не здійсниться.
1.4. Лінійне перетворення
для нормального закону
Нехай випадкова величина Х має закон розподілу N (a;
σ). Необ-
хідно знайти f (y), якщо y = kx + b.
Оскільки М(Y) = М(kх + b) = kM (x) + b = ka + b.
D(Y) = D (kx + b) = k
2
D(x) = k
2
2
σ , σ(y) =
σk
, то щільність імовір-
ностей випадкової величини Y буде мати вигляд:
f (y) =
∞<<∞−
πσ
σ
+−
−
ye
k
k
bkay
,
2
1
22
2
2
))((
.
(263)
Отже, при лінійному перетворенні випадкова величина Y також
матиме нормальний закон зі значеннями параметрів
М(Y) = ka + b,
σ=σ
ky)( .
Приклад 1. Відомо, що випадкова величина Х має закон ро-
зподілу N(– 4; 2).
Записати вирази для f (x), F(x) і накреслити їх графіки. Обчис-
лити Р(– 6 < x < 3), P(
4
+
x < 4). Чому дорівнюють Мo, Ме,
Аs, Es?
233
Розв’язання.
.
22
1
)(
;,
22
1
)(
3
)4(
3
)4(
2
2
dxexF
xexf
x
x
x
∫
π
=
∞<<∞−
π
=
∞−
+
−
+
−
Графіки f (x), F(x) наведені на рис. 97 і 98.
π
22
1
f
x
()
–
4 0
х
– 4;
π
22
1
Fx
()
–
4 0
х
1
0,5
Рис. 97 Рис. 98
Використовуючи формули (261), (262), обчислюємо ймовірності:
1)
=
⎟
⎠
⎞
⎜
⎝
⎛
+−
Φ−
⎟
⎠
⎞
⎜
⎝
⎛
+
Φ=
⎟
⎠
⎞
⎜
⎝
⎛
−−−
Φ−
⎟
⎠
⎞
⎜
⎝
⎛
−−
Φ=<<−
2
46
3
43
2
)4(6
2
)4(3
)36( xP
.84096,0)36(
;84096,03413,049966,0)1()5,3()1()5,3(
=<<−
=
+
=
Φ
+
Φ
=−Φ−
Φ
=
xР
2)
()
.9544,04772,02
2
4
244 =⋅=
⎟
⎠
⎞
⎜
⎝
⎛
Φ=<+
xP
()
.9544,044 =<+хР
Mo = Me = a = – 4; As = Es = 0.
Приклад 2. Випадкова величина Х має закон розподілу N (2; 5).
Знайти f (y), якщо у = – 2х + 1. Обчислити Р(–2 < y < 5).
Розв’язання. Оскільки М(Y) = М (kx + b) = kM(x) + b = – 2 ⋅ 2 + 1 =
= – 3, D (Y) = D (kx + b) = k
2
D (x) = 4 ⋅ 25 = 100, σ (y) = 10, то щільність
імовірностей випадкової величини Y
.,
210
1
)(
200
)3(
2
∞<<∞−
π
=
+
−
yeyf
y
Імовірність події –2 < у < 5 така:
.3085,01915,05,0)5,0()4(
2
)3(2
2
)3(5
)52( =−=Φ−Φ=
⎟
⎠
⎞
⎜
⎝
⎛
−−−
Φ−
⎟
⎠
⎞
⎜
⎝
⎛
−−
Φ=<<− yP
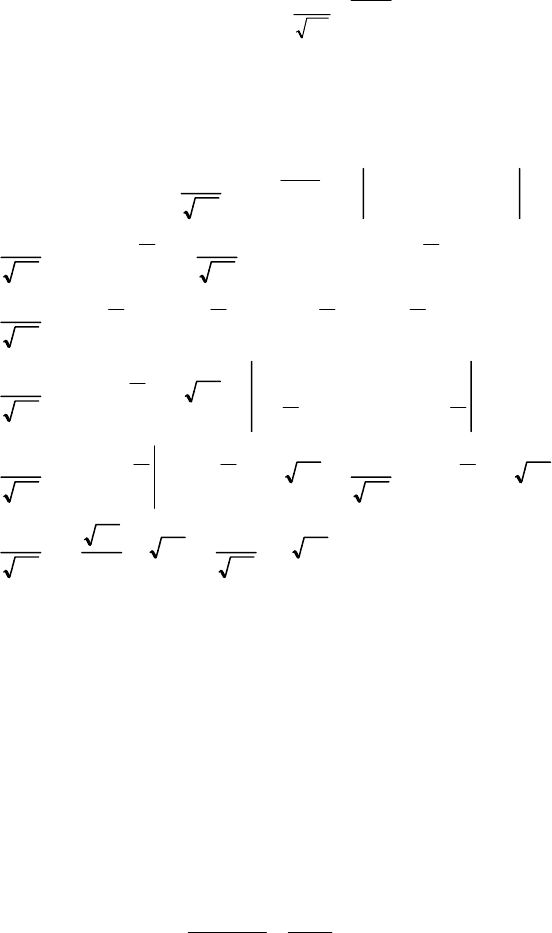
234
Приклад 3. Задано
.,
2
1
)(
2
)1(
2
∞<<∞−
π
=
+
−
xexf
x
Знайти
М(у), k
xy
, якщо у = 2х
2
– 3x + 5.
Розв’язання. Оскільки М(Y) = М(2х
2
– 3x + 5) = 2M(x
2
) – 3M(x) +
+ 5; M(XY) = M(x (2x
2
– 3x + 5)) = M(2x
3
– 3x
2
+ 5x) = 2M(x
3
) – 3M(x
2
) +
+ 5M(x) і при цьому М(х) = –1, М(x
2
) = D(x) + M
2
(x) = 1 + (–1)
2
= 2, то
нам необхідно лише знайти М(х
3
).
.4)24(
2
1
2
2
2
6
2
1
26
2
1
26
2
1
,
26
2
1
33
2
1
)133(
2
1
)1(
2
1
1
1
2
1
)()(
0
2
0
2
0
2
22
0
2
2
222
2
2
3
2
23
2
3
2
)1(
333
222
22
2
2222
22
2
−=π−
π
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
π−
π
−
π
=
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
π−−
π
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
π−
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
+−−
π
=
=
−=→=
==
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
π−−
π
=
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−+−
π
=
=−+−
π
=−
π
=
=
−=
=→=+
=
π
==
∫∫
∫
∫∫∫∫
∫∫
∫∫
∞
−
∞
−
∞
−
−−
∞
−
∞
∞−
−
∞
∞−
−
∞
∞−
−
∞
∞−
−
−
∞
∞−
∞
∞−
−
∞
∞−
∞
∞−
+
−
dzedzeze
evdvdzze
dzduzu
dzez
dzedzzedzezez
dzezzzdzez
zx
dzdxzx
dxexdxxfxxM
zzz
zz
z
zzzz
zz
x
Отже, М(х
3
) = – 4.
M(Y) = 2 ⋅ 2 – 3 ⋅ (–1) + 5 = 12;
M(XY) = 2 ⋅ (–4) – 3 ⋅ 2 + 5 ⋅ (–1) = –19;
K
xy
= M(XY) – M(X) M(Y) = –19 – (–1) ⋅ 12 = 7.
Отже, одержали: M(Y) = 12, k
xy
= 7.
Приклад 4. Відомо, що діаметр кульки підшипника D є ви-
падковою величиною, що має нормальний закон розподілу.
Бракування кульок здійснюється за таким алгоритмом: якщо
кулька не проходить через отвір із діаметром 5,5 мм, але
проходить через отвір із діаметром 5,58 мм, то її розмір від-
повідає стандарту. Якщо будь-яка із наведених умов
не ви-
конується, то кулька бракується. Визначити σ
d
, якщо брак
становить 10%.
Розв’язання. Середній діаметр кульки
m
d
=
54,5
2
08,11
2
58,55,5
==
+
мм.
235
Якщо позначимо d
1
= 5,5мм, d
2
= 5,58 мм, то ймовірність того, що
кулька буде забракована, визначається як:
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
σ
−
Φ−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
σ
−
Φ−=<<−=
d
d
d
d
mdmd
dddPP
12
21
1)(1
.
Оскільки
2
21
dd
m
d
+
=
— математичне сподівання, то виконуються
рівності:
.
2
21
22
1
22
1
22
1)(1
12
12122112
21
1
21
2
21
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
σ
−
Φ−=
=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
σ
−
Φ+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
σ
−
Φ−=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
σ
−
Φ−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
σ
−
Φ−=
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
σ
+
−
Φ−
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
σ
+
−
Φ−=<<−=
d
dddd
dd
dd
dddddddd
dd
d
dd
d
dddPP
Далі маємо:
=
σ
−
→=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
σ
−
Φ→=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
σ
−
Φ
dd
dddddd
d
2
45,0
2
9,0
2
2
121212
= ;мм024,0
3,3
5,558,5
3,3
65,1
12
=
−
=
−
=σ→
dd
d
024,0
=
σ
d
мм.
2. Двовимірний нормальний закон
(нормальний закон на площині)
Щільність імовірностей для нормального закону на площині має
вигляд
,
)(
))((
2
)(
)1(2
1
exp
12
1
),(
2
2
2
2
2
2
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
σ
−
+
σσ
−−
−
σ
−
−
−
−σπσ
=
y
y
yx
y
x
xy
x
x
xy
xyyx
ay
ayax
r
ax
r
r
yxf
∞
<
<
∞
−
∞
<
<
∞
−
y
x
,
. (264)
Тут exp (z) = e
– z
, де
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
σ
−
+
σσ
−−
−
σ
−
−
−=
2
2
2
2
2
)())((
2
)(
)1(2
1
y
y
yx
yx
xy
x
x
xy
ayayax
r
ax
r
z
;
a
x
= M(Х),
.),(),(),(
yx
xy
xyyyx
k
rYYMaXx
σσ
=σ=σ=σ=
236
Якщо r
xy
= 0, то щільність імовірностей набере такого вигляду:
.,
,
)(
)(
2
1
exp
2
1
),(
2
2
2
2
∞<<∞−∞<<∞−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
σ
−
+
σ
−
−
σπσ
=
yx
ay
ax
yxf
y
y
x
x
yx
(265)
У цьому випадку
.
2
1
2
1
)()(),(
2
2
2
2
2
)(
2
)(
y
y
x
x
ay
y
ax
x
eeyfxfyxf
σ
−
−
σ
−
−
πσπσ
==
Якщо а
х
= а
у
= 0, то
.,,
2
1
),(
2
2
2
2
2
1
∞<<∞−∞<<∞−
πσσ
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
σ
+
σ
−
yxeyxf
yx
yx
yx
(266)
У результаті перетину поверхні (264) площинами, паралельними
координатній площині хОу, і проектування перерізів на цю площину
утворюється множина подібних і однаково розташованих еліпсів зі
спільним центром на початку координат. Кожний такий еліпс — ге-
ометричне місце точок, де f (x, y) є величиною сталою. Тому еліпси
називають еліпсами рівних щільностей. Перетинаючи поверхні
(265), (266) такими площинами і проектуючи ці перерізи на коорди-
натну площину хОу, дістаємо множину кіл.
Імовірність потрапляння (Х, Y) у прямокутну область а < x < b,
c < y < d, коли K
xy
= 0, буде така:
=
ππ
=σ
πσ
σ
πσ
=
=
σ
−
<<
σ
−
→<<
σ
−
<<
σ
−
→<<
σ==
σ
−
σ==
σ
−
=
=
πσ
=
=
πσσ
==<<<<
∫∫∫∫
∫∫
∫∫∫∫
σ
−
σ
−
−
σ
−
σ
−
−
σ
−
σ
−
−
σ
−
σ
−
−
σ
−
−
σ
−
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
σ
−
+
σ
−
−
dt
y
y
y
y
edz
y
y
x
x
edy
y
y
y
y
edz
x
x
x
x
e
ad
t
ac
dyc
ab
z
aa
bxa
dtdyt
ay
dzdxz
ax
dy
y
y
edx
x
x
e
dydx
y
y
x
x
edydxyxfdycbxaP
ad
ac
t
ab
aa
z
y
ad
ac
t
y
x
ab
aa
z
x
y
y
y
y
x
x
x
x
y
y
y
x
x
x
d
c
ay
b
a
ax
x
b
a
d
c
ay
ax
b
a
yx
d
c
2222
2
)(
2
)(
)(
)(
2
1
2
2
1
2
2
1
2
2
1
2
2
1
,
,,,
2
2
2
2
2
1
2
2
2
2
2
1
),(),(
237
.
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
0
2
0
2
0
2
0
2
0
2
0
2
0
2
0
2
2222
2222
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
σ
−
Φ−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
σ
−
Φ
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
σ
−
Φ−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
σ
−
Φ=
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
π
−
π
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
π
−
π
=
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
π
+
π
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
π
+
π
=
∫∫∫∫
∫∫∫∫
σ
−
−
σ
−
−
σ
−
−
σ
−
−
σ
−
−
σ
−
−
σ
−
−
σ
−
−
y
y
y
y
x
x
x
x
ac
t
ad
t
aa
z
ab
z
ad
t
ac
z
ab
t
aa
z
acad
aaab
dtedtedzedze
dtedtedzedze
y
y
y
y
x
x
x
x
y
y
y
y
x
x
x
x
Отже,
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
σ
−
Φ−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
σ
−
Φ
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
σ
−
Φ−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
σ
−
Φ=<<<<
y
y
y
y
x
x
x
x
acad
aaab
dycbxaP ),(
. (267)
Приклад 5. Робітник на верстаті виготовляє валики. Дов-
жина Y і діаметр Х валика є незалежними випадковими ве-
личинами, що мають нормальний закон розподілу з число-
вими характеристиками: М(X) = 50 мм, σ(X) = 0,1 мм, М(Y) =
= 20 мм, σ(Y) = 0,0005 мм. Визначити відсоток бракованих
валиків, якщо валик рахується стандартним, коли його роз-
міри задовольняють умови:
(50 – 0,1) мм < х < (50 + 0,1) мм,
(20 – 0,05) мм < y < (20 + 0,05) мм.
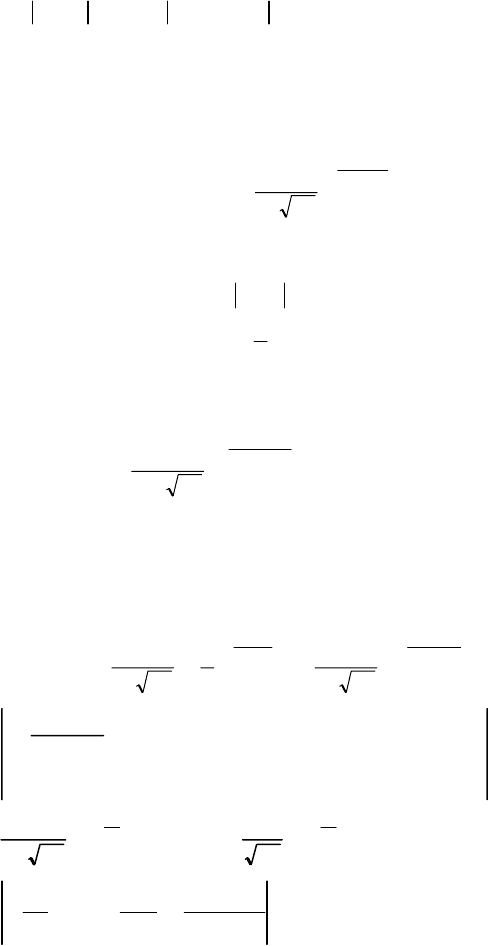
Розв’язання. Імовірність того, що валик не буде забракованим, ви-
значається імовірністю влучення розмірів (х, у) у прямокутну область,
зображену на рис. 100.
50 – 0,1 50 + 0,1
х
у
20 + 0,05
20 – 0,05
Рис. 100
(() )()
.6826,05,03413,04)10()1(4
005,0
05,0
1,0
1,0
405,0201,050
=⋅⋅=ΦΦ=
=
⎟
⎠
⎞
⎜
⎝
⎛
Φ
⎟
⎠
⎞
⎜
⎝
⎛
Φ=<−<− yxP
I
238
Імовірність браку така:
(() )
(
)
,3174,06826,015,0201,0501 =−=<−<−− yxP I
що становить 31,74%.
3. Логарифмічний нормальний
закон розподілу
Нехай Y має закон розподілу
.,
2
1
)(
2
2
2
)(
∞<<∞−
πσ
=
σ
−
−
yeyf
y
y
ay
y
Необхідно знайти f (x), якщо Х = е
y
.
Таким чином, Y є функцією випадкового аргументу Х. Тоді
.)('))(()( yyfxf ψψ=
Оскільки
.
1
)(',ln
x
xxYeX
y
=ψ=→=
Отже,
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
πσ
≤
=
σ
−
−
.0,
2
1
;0,0
)(
2
2
2
)(ln
xe
x
x
xf
y
y
ax
y
(268)
Закон розподілу випадкової величини Х із щільністю (268) нази-
вають логарифмічним нормальним законом.
3.1. Числові характеристики
1)
∫∫∫
∞
σ
−
−
∞∞
σ
−
−
=
πσ
=
πσ
==
0
2
)(ln
00
2
ln
2
2
2
2
11
2
1
)()( dxedxe
x
xdxxxfXM
y
y
y
y
ax
y
ax
y
=
σ−
−
σ
=σ+−=
=
π
=σ
πσ
=
=
∞<<∞−→∞<<σ=→
→=→+σ=→=
σ
−
=
∫∫
∞
∞−
σ+−
+σ
∞
∞−
−
+σ
+σ
2
)(
22
22
1
0,
ln
ln
2
2
2
22
22
yy
y
z
z
a
az
y
z
y
az
y
az
yy
y
y
z
z
z
dze
e
dzee
zxdzedx
exazxz
ax
y
y
yy
yy
yy
