Жлуктенко В. І., Наконечний С. І. Теорія ймовірностей і математична статистика: У 2 ч. - Ч. І. Теорія ймовірностей
Подождите немного. Документ загружается.

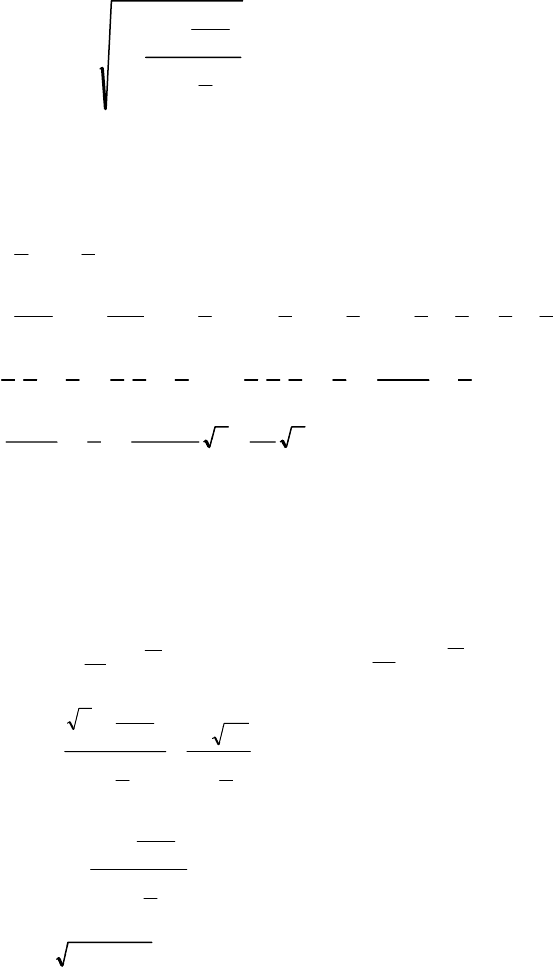
259
4.
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
−=σ
2
2
1
2
)(
2
2
k
k
kX
. (316)
Приклад 13. Випадкова величина Х має розподіл χ із k = 8
ступенями свободи. Записати вираз для f (x), F(x) і обчисли-
ти M(X), D(X), σ(X).
Розв’язання. Обчислимо гамма-функції для k = 8:
()
.6!34
2
8
2
==Γ=
⎟
⎠
⎞
⎜
⎝
⎛
Γ=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
k
=
⎟
⎠
⎞
⎜
⎝
⎛
+Γ=
⎟
⎠
⎞
⎜
⎝
⎛
Γ=
⎟
⎠
⎞
⎜
⎝
⎛
+Γ=
⎟
⎠
⎞
⎜
⎝
⎛
Γ=
⎟
⎠
⎞
⎜
⎝
⎛
Γ=
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ=
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ 1
2
5
2
7
2
7
2
7
1
2
7
2
1
4
2
9
2
18
2
1k
=
=
⎟
⎠
⎞
⎜
⎝
⎛
+Γ
⋅⋅
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ=
⎟
⎠
⎞
⎜
⎝
⎛
+Γ=
⎟
⎠
⎞
⎜
⎝
⎛
Γ 1
2
1
8
357
2
3
2
3
2
5
2
7
1
2
3
2
5
2
7
2
5
2
5
2
7
.
16
!!7
16
1357
2
1
16
357
π=π
⋅⋅⋅
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⋅⋅
=
Тут 7!! — добуток натурального ряду непарних чисел, починаючи
від 1 до 7.
У загальному вигляді
(2n – 1)!! (317)
Отже,
⎪
⎩
⎪
⎨
⎧
>
≤
=
−
.0,
48
1
;0,0
)(
2
7
2
xex
x
xf
x
⎪
⎩
⎪
⎨
⎧
>
≤
=
∫
∞
−
.0,
48
1
;0,0
)(
0
2
7
2
xdxex
x
xF
x
;
2
2!!7
2
2
1
2
)(
⎟
⎠
⎞
⎜
⎝
⎛
Γ
π
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
kk
k
XM
;393,28
2
2
1
2
)(
2
2
π−=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
−=
k
k
kXD
.393,28)( π−=σ X
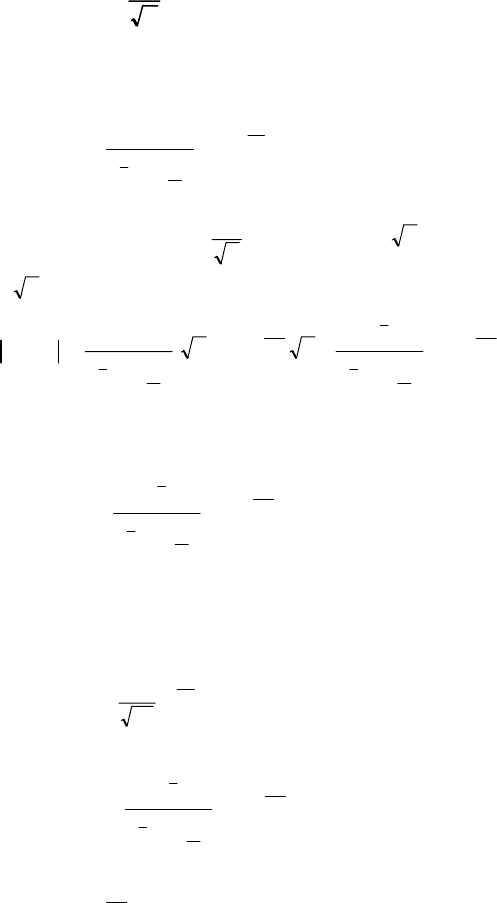
260
10.4. Розподіл
k
χ
Нехай випадкова величина Y має розподіл
χ
із k ступенями свободи
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
⎟
⎠
⎞
⎜
⎝
⎛
Γ
≤
=
−
−
−
.0,
2
2
1
;0,0
)(
2
1
1
2
2
yey
k
y
yf
y
k
k
Необхідно знайти f (x), якщо
k
Y
X
=
. Оскільки Y =
k
Х =
ψ
(х) і
при цьому
k
x
=ψ
′
, то
(
)
=ψ
′
ψ= )()()( xxfxf
()
2
1
1
2
2
2
1
1
2
22
2
2
2
2
1
kx
k
k
k
kx
k
k
ex
k
k
kexk
k
−
−
−
−
−
−
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
.
Отже,
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
⎟
⎠
⎞
⎜
⎝
⎛
Γ
≤
=
−
−
−
.0,
2
2
;0,0
)(
2
1
1
2
2
2
xex
k
k
x
xf
kx
k
k
k
(318)
10.5. Розподіл Стьюдента
Незалежні випадкові величини Y і Х мають закони розподілу:
;,
2
1
)(
2
2
∞<<∞−
π
=
−
yeyf
y
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
⎟
⎠
⎞
⎜
⎝
⎛
Γ
≤
=
−
−
−
.0,
2
2
;0,0
)(
2
1
1
2
2
2
xex
k
k
x
xf
kx
k
k
k
Знайти f (z), якщо
X
Y
Z
=
. Для зручності подальших перетворень
запишемо f (x) у вигляді
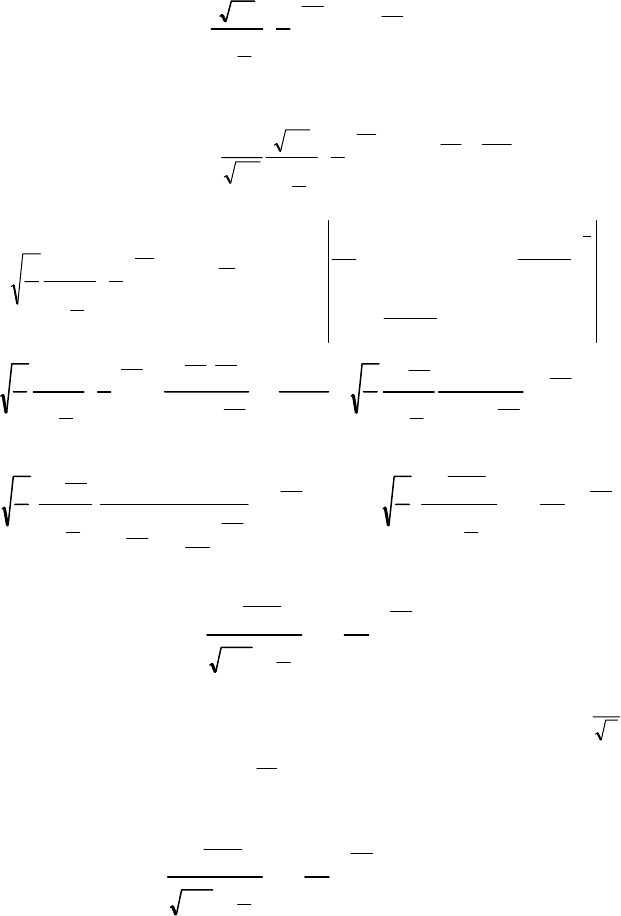
261
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
≤
=
−
−
−
.0,
2
2
Г
2
;0,0
)(
2
1
2
1
2
xex
k
k
k
x
xf
kx
k
k
Використовуючи формулу (217), дістаємо:
∫∫
∞
−
∞
−
−
−
=
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
Γ
π
==
0
2
0
2
1
2
1
222
2
2
2
2
1
)()()(
dxeex
k
k
k
xdxzxfxfzf
zxkx
k
k
=
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
=→=+
=
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
Γ
π
=
∫
∞
+−
−
−
2
2
1
2
2
2
0
)(
2
1
2
1
2
)(
2
2
2
1
2
2
zk
dt
dxx
zk
t
xtzk
x
dxxex
k
k
k
zk
x
k
k
()
()
()
=
+
⎟
⎠
⎞
⎜
⎝
⎛
Γ
π
=
+
+
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
Γ
π
=
−
∞
−
+
−
−
∞
−
−−
−
∫∫
dtet
zk
k
kk
zk
dt
e
zk
tk
k
k
t
k
k
k
t
k
kk
k
0
2
1
2
1
2
2
1
2
0
2
1
2
2
1
2
1
2
1
1
2
2
2
2
1
()
()
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
π
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
Γ
π
=
+
−
−
∞
−
+
+
+
−
∫
2
1
2
0
1
2
1
2
1
2
2
1
2
1
1
2
2
1
1
1
2
k
t
k
k
k
k
k
z
k
k
k
k
dtet
k
z
k
k
kk
.1
2
2
1
2
1
2
+
−
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
Γπ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
k
k
z
k
k
k
Отже, якщо Y має розподіл N (0, 1), а випадкова величина Х –
k
χ
,
то випадкова величина
X
Y
Z
=
характеризуватиметься розподілом
Стьюдента зі щільністю ймовірностей
.,1
2
2
1
)(
2
1
2
∞<<∞−
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
Γπ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
+
−
z
k
z
k
k
k
zf
k
(319a)
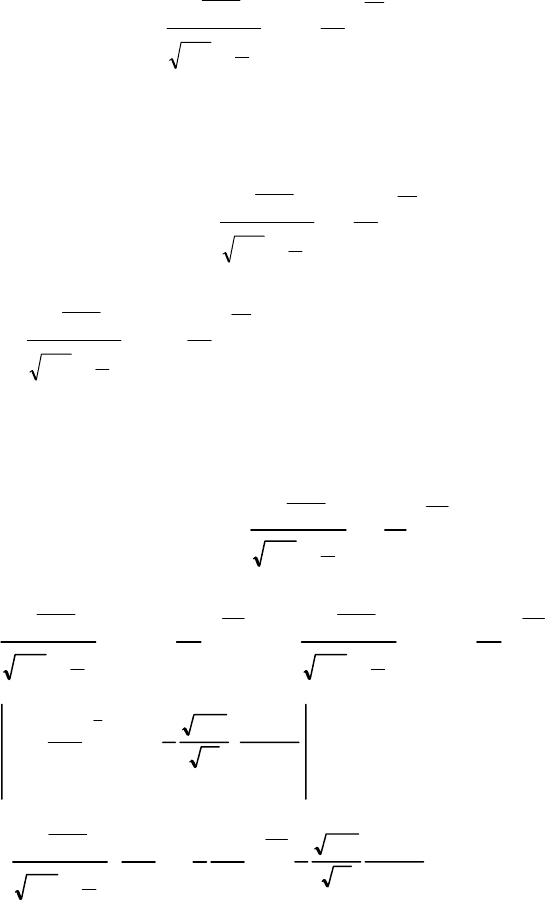
262
Тоді функція розподілу ймовірностей
∫
∞−
+
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
Γπ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
z
k
dz
k
z
k
k
k
zF
2
1
2
1
2
2
1
)(
. (319б)
10.5.1. Числові характеристики
розподілу Стьюдента
1.
∫
∞
∞−
==
dzzfzZM
)()( =
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
Γπ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
+
−
∞
∞−
∫
dz
k
z
k
k
k
z
k
2
1
2
1
2
2
1
∫
∞
∞−
+
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
Γπ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
= 01
2
2
1
2
1
2
dz
k
z
z
k
k
k
k
.
Оскільки підінтегральна функція є непарною, а межі інтегруван-
ня симетричні відносно нуля:
0)(
=
ZM
. (320)
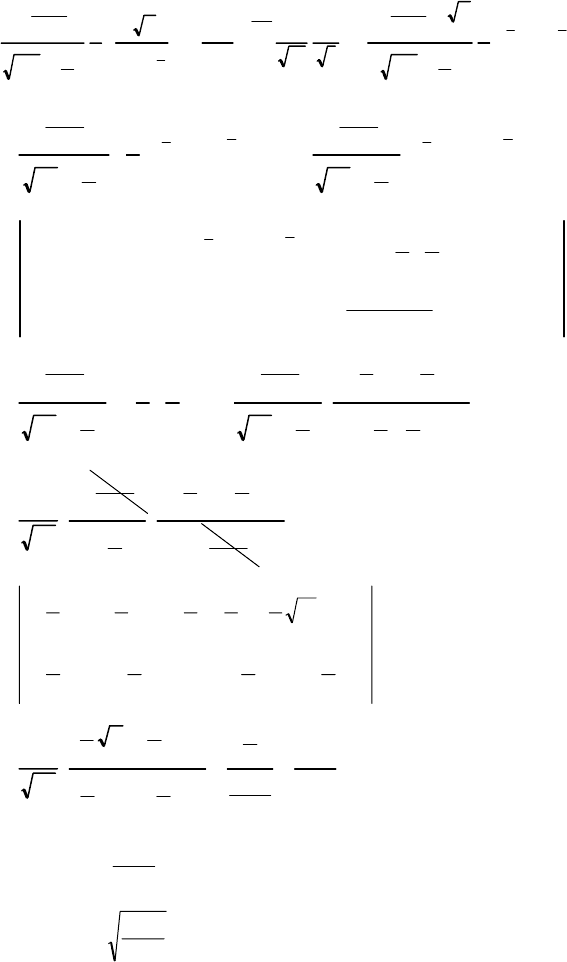
2.
∫
∞
∞−
==
dzzfzZM
)()(
22
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
Γπ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
+
−
∞
∞−
∫
dz
k
z
k
k
k
z
k
2
1
2
2
1
2
2
1
∫∫
∞
∞−
+
−
∞
∞−
+
−
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
Γπ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
Γπ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
= dz
k
z
z
k
k
k
dz
k
z
z
k
k
k
kk
2
1
2
2
2
1
2
2
1
2
2
1
21
2
2
1
=
<<→∞<<
−
−
=
⎟
⎠
⎞
⎜
⎝
⎛
−
=
=
100
)1(
1
2
1
,
1
2
2
1
tz
t
kdt
kt
t
dz
t
kt
z
∫
=
−
−
⎟
⎠
⎞
⎜
⎝
⎛
−
+
−
⎟
⎠
⎞
⎜
⎝
⎛
Γπ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
+
−
1
0
2
2
1
)1(
1
2
1
1
1
1
1
2
2
1
2
t
kdt
kt
t
t
kt
kt
kt
k
k
k
k
263
()
∫∫
=−
⎟
⎠
⎞
⎜
⎝
⎛
Γπ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
−
+
−
⎟
⎠
⎞
⎜
⎝
⎛
Γπ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
−
+
−
1
0
2
22
1
1
0
2
1
2
5
)1(
2
1
2
2
1
2
1
1
1
1
2
1
2
2
1
2 dttt
k
k
kk
k
t
kdt
kt
t
t
t
tkk
k
k
k
k
k
∫∫
=−
⎟
⎠
⎞
⎜
⎝
⎛
Γπ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=−
⎟
⎠
⎞
⎜
⎝
⎛
Γπ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
−
⎟
⎠
⎞
⎜
⎝
⎛
−
−
−
⎟
⎠
⎞
⎜
⎝
⎛
−
1
0
11
2
1
2
3
1
0
11
2
2
1
)1(
2
2
1
)1(
2
1
2
2
2
1
dttt
k
k
k
dttt
k
k
k
kk
=
+Γ
ΓΓ
=
⎟
⎠
⎞
⎜
⎝
⎛
−=−
=
∫
−
⎟
⎠
⎞
⎜
⎝
⎛
−
−
дістаємо,
)(
)()(
);(ункціїф-бетаювластивіст
ззгідноi1
2
;
2
3
)1(нняеспіввідношЗі
1
0
11
2
1
2
3
qр
qр
qрВ
k
Вdttt
k
=
⎟
⎠
⎞
⎜
⎝
⎛
−+Γ
⎟
⎠
⎞
⎜
⎝
⎛
−Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γπ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
Γπ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
1
22
3
1
22
3
2
2
1
1
2
;
2
3
2
2
1
k
k
k
k
k
k
В
k
k
k
=
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
⎟
⎠
⎞
⎜
⎝
⎛
−Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
π
=
2
1
1
22
3
2
2
1
k
k
k
k
k
=
⎟
⎠
⎞
⎜
⎝
⎛
−Γ
⎟
⎠
⎞
⎜
⎝
⎛
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
−Γ=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
π=
⎟
⎠
⎞
⎜
⎝
⎛
Γ=
⎟
⎠
⎞
⎜
⎝
⎛
+Γ=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
1
2
1
2
11
22
;
2
1
2
1
2
1
1
2
1
2
3
kkkk
.
2
2
2
2
1
2
1
2
1
22
1
−
=
−
=
⎟
⎠
⎞
⎜
⎝
⎛
−Γ
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−Γπ
π
=
k
k
k
k
kk
k
k
3.
2
)(
−
=
k
k
ZD
. (321)
4.
2
)(
−
=σ
k
k
Z
. (322)
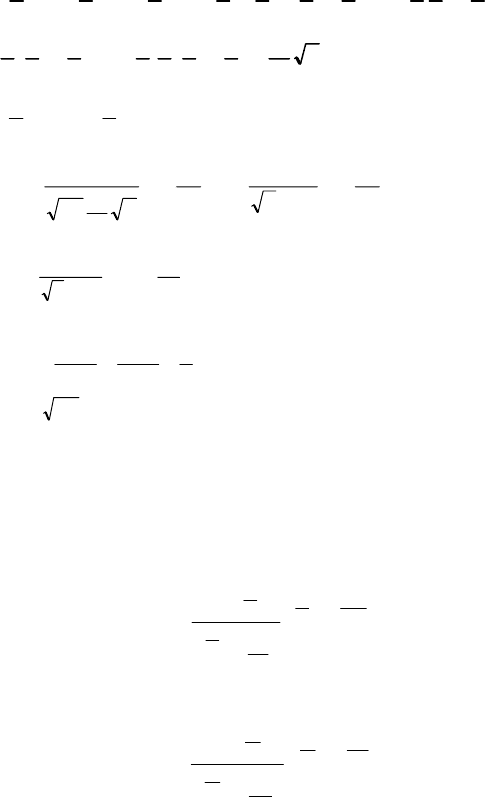
264
Приклад 14. Випадкова величина Х має розподіл Стьюден-
та із k = 7 ступенями свободи. Записати вираз для f (x), F(x)
і обчислити M(X), D(X), σ(X).
Розв’язання. За заданим числом ступеней свободи k = 7 обчислимо
гамма-функції:
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ=
⎟
⎠
⎞
⎜
⎝
⎛
+Γ=
⎟
⎠
⎞
⎜
⎝
⎛
Γ=
⎟
⎠
⎞
⎜
⎝
⎛
+Γ=
⎟
⎠
⎞
⎜
⎝
⎛
Γ=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
2
3
2
3
2
5
1
2
3
2
5
2
5
2
5
1
2
5
2
7
2
k
;
8
15
2
1
2
1
2
3
2
5
1
2
1
2
3
2
5
π=
⎟
⎠
⎞
⎜
⎝
⎛
Γ=
⎟
⎠
⎞
⎜
⎝
⎛
+Γ=
()
6!341
2
7
1
2
==Γ=
⎟
⎠
⎞
⎜
⎝
⎛
+Γ=
⎟
⎠
⎞
⎜
⎝
⎛
+Γ
k
;
∞<<∞−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
π⋅
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
ππ
=
−−
x
xx
xf ,
7
1
157
48
7
1
8
15
7
6
)(
4
2
4
2
;
∫
∞
∞−
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
π⋅
= dx
x
xF
4
2
7
1
157
48
)(
;
;0)( =XM
4,1
5
7
27
7
2
)( ==
−
=
−
=
k
k
XD
;
18,1.4,1)( ≈=σ X
.
10.6. Розподіл Фішера—Снедекора
Нехай задано дві незалежні випадкові величини Y і Х, які мають
закони розподілу:
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
⎟
⎠
⎞
⎜
⎝
⎛
Γ
≤
=
−−
.0,
2
2
;0,0
)(
2
1
2
1
2
2
1
11
1
1
xex
k
k
x
xf
xkk
k
k
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
⎟
⎠
⎞
⎜
⎝
⎛
Γ
≤
=
−−
.0,
2
2
;0,0
)(
2
1
2
2
2
2
2
22
2
2
yey
k
k
y
yf
ykk
k
k
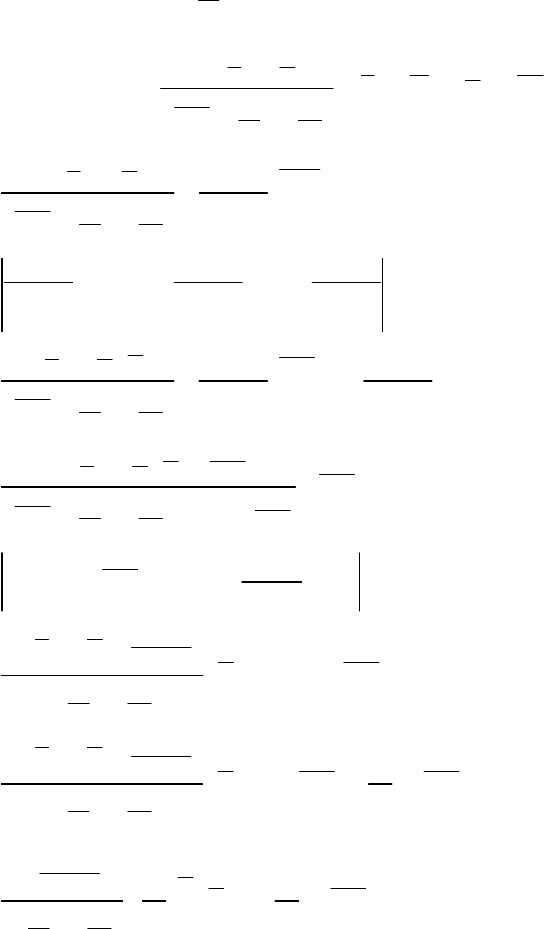
265
Знайти f (z), якщо Z =
X
Y
. Оскільки Y = ZХ і при цьому 0 < x <
∞
;
0 < y <
∞
; 0 < z <
∞
, то згідно з (217), дістаємо:
()()
()
∫∫
∞∞
−
−
−−
+
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
==
00
2
1
2
2
1
2
21
2
2
2
2
1
2
2
11
21
21
22
2
)()()(
dxxezxex
kk
kk
dxzxfxfzf
zxk
k
xkk
kk
kk
()()
=
∞<<∞<<
+
=→
+
=→=
+
=
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
+
∞
+
∫
zx
zkk
dt
dx
zkk
t
xtx
zkk
dx
zkk
t
kk
kk
x
zkk
kk
kk
0,0
22
2
2
22
2
2121
21
2
0
21
21
2
2
2
2
1
21
21
21
()()
∫
∞
−
−
+
+
−
=
+
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
0
21
1
2
21
21
2
1
2
2
2
2
1
22
22
2
21
21
2
21
zkk
dt
e
zkk
t
kk
zkk
t
kk
kk
k
kk
()()
()
=
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ==
=
+
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
∫
∫
∞
−
−
+
∞
−
−
+
+
+
+
−
тооскільки ,
2
22
2
2
21
0
1
2
0
1
2
2
21
21
2
2
1
2
2
2
2
1
21
21
21
21
212
21
kk
dtet
dtet
zkk
kk
zkk
t
kk
t
kk
kk
kk
kkk
kk
()()
=+
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
+
−−
2
21
1
2
21
21
2
2
2
1
212
21
)(
22
2
kkk
kk
zkkz
kk
kk
kk
()()
()
=+
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
+
−
+
−−
2
1
2
2
1
1
2
21
21
2
2
2
1
21212
21
)1(
22
2
kkkkk
kk
z
k
k
kz
kk
kk
kk
.)1(
22
2
2
1
2
1
2
1
2
21
21
212
1
2
kkk
k
k
z
k
k
z
k
k
kk
kk
+
−−
+
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
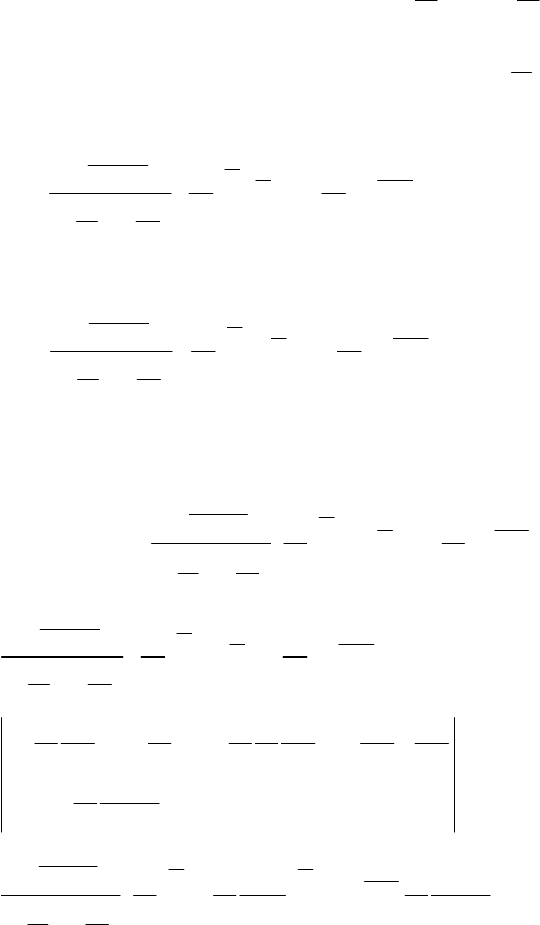
266
Отже, якщо випадкова величина Х має розподіл
1
2
k
χ
, а Y —
2
2
k
χ
, де
k
1
— число ступенів свободи випадкової величини Х, k
2
— число
ступенів свободи Y, і при цьому Х і Y не корельовані, то Z =
X
Y
має
розподіл Фішера—Снедекора зі щільністю ймовірностей
⎪
⎪
⎩
⎪
⎪
⎨
⎧
≥+
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
<
=
+
−−
.0,)1(
22
2
;0,0
)(
2
1
2
1
2
1
2
21
21
212
1
2
zz
k
k
z
k
k
kk
kk
z
xf
kkk
k
k
(323)
Функція розподілу ймовірностей
⎪
⎪
⎩
⎪
⎪
⎨
⎧
≥+
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
<
=
∫
+
−−
.0,)1(
22
2
0,0
)(
0
2
1
2
1
2
1
2
21
21
212
1
2
zdzz
k
k
z
k
k
kk
kk
z
xF
z
kkk
k
k
(324)
10.6.1. Числові характеристики
розподілу Фішера—Снедекора
1.
∫
∞
∞−
== dzzfzZM
)()(
∫
=+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
+
−−
z
kkk
k
k
dzz
k
k
zz
k
k
kk
kk
0
2
1
2
1
2
1
2
21
21
212
1
2
)1(
22
2
∫
=+
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
+
−
z
kkk
k
k
dzz
k
k
z
k
k
kk
kk
0
2
1
2
2
1
2
21
21
212
1
2
)1(
22
2
=
<<→∞<<→
−
=
−
=
−
+=
−
+=+→
−
=
=
100
)1(
1
1
1
1
1
11
1
2
2
1
2
1
1
2
1
2
2
1
tz
t
dt
k
k
dz
tt
t
t
t
k
k
k
k
z
k
k
t
t
k
k
z
()
∫
=
−
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
+
1
0
2
2
1
2
2
2
1
1
2
21
21
)1(
)1(
1
22
2
21
2
1
2
t
dt
k
k
t
t
t
k
k
k
k
kk
kk
kk
k
k
k
267
()
∫
=
−
−
−
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
+
1
0
2
2
1
2
2
2
2
2
1
1
2
21
21
)1(
)1(
1
22
2
21
2
2
2
1
2
t
dt
k
k
t
t
t
k
k
k
k
kk
kk
kk
k
k
k
k
k
()
=−
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
−
∫
dttt
k
k
k
k
k
k
kk
kk
k
k
k
k
k
k
2
2
1
0
2
2
1
2
1
1
2
21
21
1
2
1
2
1
2
1
22
2
=
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+Γ
⎟
⎠
⎞
⎜
⎝
⎛
+Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
−+=
=−=−
=
∫∫
−
⎟
⎠
⎞
⎜
⎝
⎛
−−
⎟
⎠
⎞
⎜
⎝
⎛
+
−
2
1
2
1
2
1
2
;1
2
)1()1(
21
21
12
1
0
1
0
11
2
11
2
2
22
12
12
kk
kk
kk
B
dtttdttt
kk
kk
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
−Γ
⎟
⎠
⎞
⎜
⎝
⎛
+Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
⎟
⎠
⎞
⎜
⎝
⎛
−Γ
⎟
⎠
⎞
⎜
⎝
⎛
+Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
22
1
2
1
2
2
1
2
1
2
22
2
21
12
2
1
21
12
21
21
2
1
kk
kk
k
k
kk
kk
kk
kk
k
k
.
2
1
2
2
2
1
2
1
2
1
222
1
1
1
2
2
1
211
122
2
1
−
=
−
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
−Γ
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
k
k
k
k
k
k
kkk
kkk
k
k
.
2
)(
1
1
−
=
k
k
ZM
(325)
2.
∫
∞
∞−
== dzzfzZM )()(
22
=
∫
=+
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
+
−−
z
kkk
k
k
dzz
k
k
zz
k
k
kk
kk
0
2
1
2
1
2
2
1
2
21
21
212
1
2
)1(
22
2
∫
=+
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
+
−+
z
kkk
k
k
dzz
k
k
z
k
k
kk
kk
0
2
1
2
1
2
1
2
21
21
212
1
2
)1(
22
2
268
==
дістанемо),(визначенніпри
іякзаміну,самутакуЗдіснивши
zМ
()
∫
=
−
−
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
+
+
1
0
2
2
1
2
1
2
2
1
1
2
21
21
)1(
)1(
1
2
Г
2
2
21
2
1
2
t
dt
k
k
t
t
t
k
k
k
k
kk
kk
kk
k
k
k
∫
=−
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
−+
1
0
3
2
1
2
2
2
1
2
2
1
1
2
21
21
12
2
1
2
)1(
22
2
dttt
k
k
k
k
k
k
kk
kk
kk
л
k
k
∫
=−
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
−+
1
0
3
2
1
2
2
2
1
21
21
12
)1(
2
Г
2
2
dttt
k
k
kk
kk
kk
() ()
=
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
⎟
⎠
⎞
⎜
⎝
⎛
−Γ
⎟
⎠
⎞
⎜
⎝
⎛
+Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
−+=
=−=−
=
−
⎟
⎠
⎞
⎜
⎝
⎛
−−
⎟
⎠
⎞
⎜
⎝
⎛
+
−
+
∫∫
2
2
2
2
2
2
2
;2
2
11
21
12
12
12
2
1
0
12
2
3
2
1
0
1
2
12
1
2
kk
kk
kk
B
dtttdttt
kk
k
k
=
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
−Γ
⎟
⎠
⎞
⎜
⎝
⎛
+Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
⎟
⎠
⎞
⎜
⎝
⎛
−Γ
⎟
⎠
⎞
⎜
⎝
⎛
+Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
22
2
2
2
2
2
2
2
2
2
22
2
21
12
2
2
2
1
21
12
21
21
2
2
2
1
kk
kk
k
k
kk
kk
kk
kk
k
k
=
⎟
⎠
⎞
⎜
⎝
⎛
−Γ
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−=
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
−Γ
⎟
⎠
⎞
⎜
⎝
⎛
−=
⎟
⎠
⎞
⎜
⎝
⎛
−Γ
⎟
⎠
⎞
⎜
⎝
⎛
−=
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
−Γ=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+=
⎟
⎠
⎞
⎜
⎝
⎛
+Γ
⎟
⎠
⎞
⎜
⎝
⎛
+=
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
+Γ=
⎟
⎠
⎞
⎜
⎝
⎛
+Γ
=
2
2
2
2
1
2
12
2
1
2
1
2
1
2
11
22
22
1
2
2
2
1
2
11
2
2
2
111
111111
2222222
kkk
kkkkkk
kkkkkkk
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
−Γ
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
=
2
2
2
2
2
1
2
2
222
1
2
2111
1222
2
2
2
1
kkkk
kkkk
k
k
.
)4()2(
)2(
)4()2(
)2(
112
2
2
1
11
22
2
2
2
1
−−
+
=
−−
+
kkk
kk
kk
kk
k
k
