Жлуктенко В. І., Наконечний С. І. Теорія ймовірностей і математична статистика: У 2 ч. - Ч. І. Теорія ймовірностей
Подождите немного. Документ загружается.

239
.2
22
22
2
2
2
2
2
)(
2
2
)(
2
2
2
2
2
2
2
2
2
y
y
y
y
y
y
y
y
y
yy
y
a
a
t
a
y
z
a
z
a
e
e
dte
e
dtdz
tz
dze
e
dze
e
σ
+
σ
+
∞
∞−
−
σ
+
∞
∞−
σ−
−
σ
+
∞
∞−
σ−
−
σ
−
=π
π
=
π
=
=
=σ−
=
=
π
=
π
=
∫
∫∫
()
2
2
у
у
а
еХМ
σ
+
= . (269)
2.
.
2
11
2
1
)()(
0
2
)(ln
00
2
)(ln
222
2
2
2
2
dxxedxe
x
xdxxfxXM
y
y
y
y
ax
y
ax
y
∫∫∫
∞
σ
−
−
∞∞
σ
−
−
πσ
=
πσ
==
Виконуючи таку саму заміну, як і для знаходження М(Х), дістаємо:
).1(
)()()(
.)(
;2
222
22
1
2
1
22
22
2
2
2
2
2
2
2
2
2
222
2
222
2
22
22
22
2
22
22
2
)2(
22
2
)2(
2
2
2
2
2
2
22
2
−=
=−=−=−=
=
=π
π
=
π
=
π
=
=
π
=
π
=σ
πσ
σσ+
σ+σ+
σ
+
σ+
σ+
σ+
σ+
∞
∞−
σ−
−
σ+
∞
∞−
σ−
−σ
∞
∞−
−σ
∞
∞−
−+σ
+σ
−
∞
∞−
+σ
∫∫
∫∫∫
yyy
yyyy
y
y
yy
yy
yy
yy
y
yy
y
y
y
y
y
yy
yyyy
ee
eeeeXMXMXD
eXM
e
e
dze
e
dze
e
dze
e
dzedzeee
a
aa
a
a
a
a
a
z
a
z
a
z
z
a
z
az
az
y
z
az
y
3.
)1()(
22
2
−=
σσ+
yyy
eeXD
a
. (270)
Приклад 6. Випадкова величина Х має закон розподілу
N (2; 4). Знайти математичне сподівання і дисперсію для ло-
гарифмічного нормального закону випадкової величини Y.
Розв’язання. М(Y) =
.
10
2
2
ee
y
x
a
=
σ
+
).1()1()1()(
1620161622
2
22
−=−=−=
+⋅
σσ+
eeeeeeYD
xxx
a
4. Урізаний (ліворуч) нормальний закон
Нормальний закон посідає особливе місце в теорії ймовірностей
та математичній статистиці, особливо у прикладних задачах. Але іс-
нує певний клас задач, які характерні для теорії надійності, коли ви-
падкова величина Х може набувати лише додатні числові значення.
У цьому разі використовують урізаний ліворуч нормальний закон,
що
зображений на рис. 101 для а > 0.
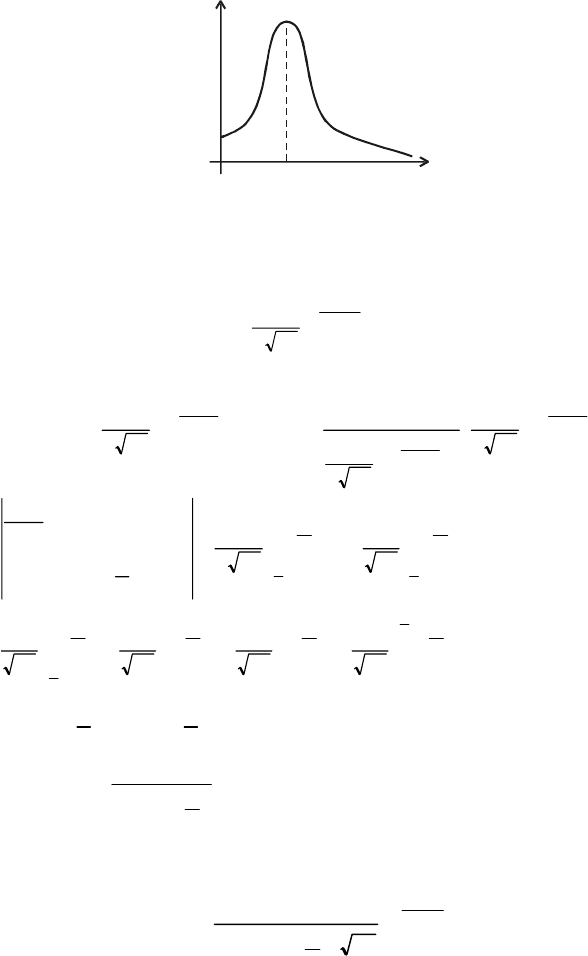
240
0
a x
fx
()
Pис. 101
Щільність імовірностей цього закону буде така:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
πσ
≤
=
σ
−
−
.0,
2
0,0
)(
2
2
2
)(
xe
C
x
xf
ax
Сталу С знаходимо з умови нормування:
.5,05,0
2
1
2
1
2
1
2
1
2
1
2
1
0
,
2
1
;
2
1
1
1
2
1)(
0
2
0
2
0
2
0
2
22
0
2
)(
0
0
2
)(
0
2
)(
2222
22
2
2
2
2
2
2
⎟
⎠
⎞
⎜
⎝
⎛
σ
Φ+=
⎟
⎠
⎞
⎜
⎝
⎛
σ
−Φ−=
=
π
−
π
=
π
+
π
=
=
π
=σ
πσ
=
∞<<
σ
−→∞<<
σ==
σ
−
=
=
πσ
πσ
=→=
πσ
→=
∫∫∫∫
∫∫
∫∫
∫
∫
σ
−
−
∞
−
∞
−
σ
−
−
∞
σ
−
−
∞
σ
−
−
∞
σ
−
−
∞
∞
σ
−
−
∞
σ
−
−
аа
dzedzedzedze
dzedze
z
a
x
dzdxz
ax
dxe
dxe
Cdxe
C
dxxf
a
zzz
a
z
a
z
a
z
ax
ax
ax
Звідси
⎟
⎠
⎞
⎜
⎝
⎛
σ
Φ+
=
а
С
5,0
1
.
Отже,
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
π
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
σ
Φ+σ
≤
=
σ
−
−
;0,
25,0
1
;0,0
)(
2
2
2
)(
xe
а
x
xf
ax
(271)
241
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
π
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
σ
Φ+σ
≤
=
σ
−
−
∫
.0,
25,0
1
;0,0
)(
2
2
2
)(
0
xe
а
x
xF
ax
x
(272)
4.1. Числові характеристики
1.
=
πσ
==
∫∫
∞
σ
−
−
∞
dxxe
C
dxxxfXM
ax
0
2
)(
0
2
2
2
)()(
;
2
1
Ф5,0
5,0
5,0
2
5,0
2
22
)(
2
)(
2
0
,
2
2
2
2
2
222
2
2
2
2
222
2
π
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
σ
+
σ
+=
=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
σ
Φ+
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
σ
Φ+
+
π
σ
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
σ
Φ++−
π
σ
=
=
π
+
π
σ
=+σ
π
=
=σ+σ
πσ
=
∞<<
σ
−→∞<<
σ=+σ=→=
σ
−
σ
−
σ
−
∞
σ
−
−
∞
σ
−
−
∞
σ
−
−
∞
σ
−
−
∞
σ
−
−
∫∫∫
∫
a
a
a
z
a
z
a
z
a
z
a
z
e
a
a
a
a
ae
C
a
Cae
C
dze
Ca
dzze
C
dzeaz
C
dzeaz
C
z
a
x
dzdxazxz
ax
2
2
2
25,0
)(
σ
−
π
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
σ
Φ+
σ
+=
a
e
a
aXM
. (273)
2.
=
πσ
==
∫∫
∞
σ
−
−
∞
dxex
C
dxxfxXМ
ax
0
2
)(
2
0
22
2
2
2
)()(
.
2
2
22
)2(
2
)(
2
2
2
22
22
2
222
2
2
222
22
∫∫∫
∫∫
∞
σ
−
∞
σ
−
∞
σ
−
−−−
∞
σ
−
−
∞
σ
−
−
π
+σ
π
+σ
π
=
=+σ+σ
π
=σ+σ
πσ
=
aaa
zzz
a
z
a
z
dzea
C
dzzea
C
dzez
C
dzeaazz
C
dzeaz
C
242
1)
=
−=→=
==
=σ
π
∫
∞
σ
−
−−
−
a
zz
z
evdvdzze
dzduzu
dzez
C
22
2
22
22
2
,
2
.
22
5,0
5,0
22
5,0
22
2
2
2
2
2
2
22
2
22
2
2
2
22
2
σ
−
σ
−
σ
−
∞
σ
−
−
∞
σ
−
−
π
σ
+
π
σ
=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
σ
Φ+
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
σ
Φ+
π
σ
+σ
π
=
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
σ
Φ++
σ
σ
π
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+−σ
π
=
∫
aa
a
a
z
a
z
e
Ca
a
a
ea
C
a
e
aC
dzeze
C
2)
.2
2
2
2
2
2
2
2
22
2
22
σ
−
∞
σ
−
∞
σ
−
−−
σ
π
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−σ
π
=σ
π
∫
a
a
a
zz
ae
C
ea
C
dzzea
C
3)
.
2
5,0
5,0
2
5,0
22
22
2
2
2
2
π
=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
σ
+
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
σ
+
π
=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
σ
+
π
=
π
∫
∞
σ
−
−
а
а
Ф
а
Ф
a
a
Фa
C
dzea
C
a
z
.
22222
2
22
)(
2
2
22
22
2
2
2
2
2
2
2
2
π
+
π
σ
+
π
σ
=
π
+
π
σ
+
π
σ
−
π
σ
=
σ
−
σ
−
σ
−
a
e
Caa
e
Ca
e
Ca
XM
aaa
3.
=−= )()()(
22
XMXMXD
2
2
2
2
2
2
2
2
2
5,0
2
5,0
2
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
σ
Φ+
σ
+−
π
+−
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
σ
Φ+
σ
+
π
σ
=
σ
−
σ
−
aa
e
a
a
a
e
a
a
(274)
Приклад 7. За заданим N (2; 4) записати f (x), F(x) для уріза-
ного нормального закону (ліворуч) і знайти М(Х), D(X).
Розв’язання. Використовуючи (273) — (276), одержимо:
⎪
⎩
⎪
⎨
⎧
>
π
<
=
⎪
⎩
⎪
⎨
⎧
>
π
<
=
∫
−
−
−
−
x
xx
xdxe
x
xF
xe
x
xf
0
32
)2(
32
)2(
.0,
2766,2
1
;0,0
)(
;0,
2766,2
1
;0,0
)(
.)79,52(
2
57,11
2
16
)(;
2
446,1
2)(
2
8
1
8
1
8
1
−−−
+−
π
+
π
=
π
+= eeXDeXM
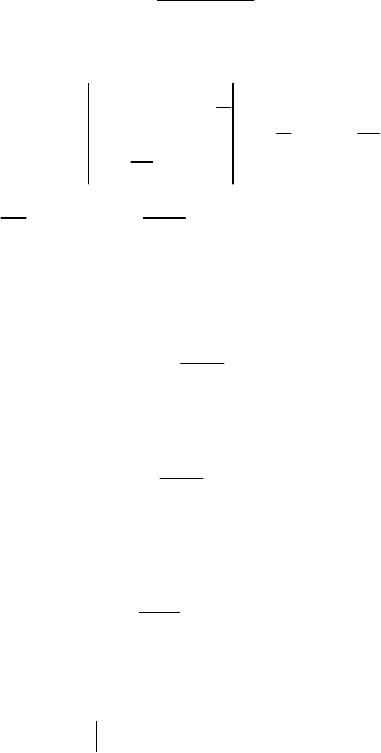
243
5. Гамма-розподіл
Неперервна випадкова величина Х має гамма-розподіл імовір-
ностей, якщо
⎩
⎨
⎧
≥
<
=
λ−−α
,0,
;0,0
)(
1
xeCx
x
xf
x
де
0,0 >
λ
>α
, С — константа, яка визначається із умови нормування:
.
1
0
1
∫
∞
λ−−α
=
dxex
C
x
Тут
,
)(
1
,
0
1
1
00
1
α
−
∞
−α
α
−
−α
∞∞
λ−−α
λ
αΓ
=
λ
=
=
λ
⎟
⎠
⎞
⎜
⎝
⎛
λ
=
λ
=
λ
==λ
=
∫
∫∫
dzez
dz
e
z
dz
dx
z
xzx
ex
z
zx
де
∫
∞
−−α
=αΓ
0
1
)( dzez
z
називають гамма-функцією.
Таким чином,
)(αΓ
λ
=
α
C . (275)
Тоді
⎪
⎩
⎪
⎨
⎧
>
αΓ
λ
≤
=
λ−−α
α
.0,
)(
;0,0
)(
1
xeх
x
xf
x
(276)
Функція розподілу ймовірностей
⎪
⎩
⎪
⎨
⎧
≥
α
λ
<
=
∫
λ−−α
α
х
х
xdxех
Г
x
xF
0
1
.0,
)(
;0,0
)(
(277)
Отже, гамма-розподіл визначається двома параметрами
α
і
λ
.
Розглянемо властивості гамма-функції:
1.
;1)1(
0
0
=−==Γ
∞
∞
−−
∫
zz
edzе
244
2.
(
)
∫∫∫
∞
−
−
∞
−
−
∞
−
=======Γ
0
2
0
2
1
0
1
2
1
,
2
2
1
tdtdz
t
zdz
z
e
dzezdzez
z
zz
∫∫
∞
−
∞
−
π=
π
===
0
2
0
2
2
.
2
2
22
2
2
2
dte
t
tdte
t
t
.
2
1
π=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
(278)
3. Установимо зв’язок між гамма-функціями
).(і)1( α
Γ
+
α
Γ
∫
∫
∞
−−α
∞
−α
=αΓ
=+αΓ
0
1
0
.)(
,)1(
dzez
dzez
z
z
Зінтегруємо
).1( +αΓ
.)(
,
)1(
0
1
0
1
0
0
1
∫∫
∫
∞
−−α
∞
−−α
∞
−α
∞
−−
−αα
−α
αΓα=α=α+−=
=
−=→=
α==
==+αΓ
dzezdzezez
evdvdze
dzzduzu
dzez
zzz
zz
z
Отже,
)()1(
α
Γ
α
=
+
α
Γ
. (279)
Якщо, наприклад,
α
= n, де n — ціле невід’ємне число, то:
Г(n + 1) = nГ(n).
Використовуючи рівність (278) для Г(n), дістаємо:
Г(n) = (n – 1)Г(n – 1),
для Г(n – 1) рівність (278) набуде такого вигляду:
Г(n – 1) = (n – 2)Г(n – 2)
і так для кожного цілого значення аргументу
α
гамма-функції.
Таким чином,
Г(n + 1) = n Г (n) = n(n – 1) Г (n – 1) =
= n (n – 1) (n – 2)Г(n – 2) = … =
= n(n – 1)(n – 2) … Г(1) = n(n – 1)(n – 2) … 1 = n!
Отже,
Г(n + 1) = n! (280)
Так, наприклад, Г(6) = 5! = 5
⋅
4
⋅
3
⋅
2
⋅
1 = 120.

245
5.1. Числові характеристики
1.
∫∫∫
∞∞
λ−α
α
∞
λ−−α
α
=
λ
=
λ
==λ
=
αΓ
λ
=
αΓ
λ
==
000
1
,
)()(
)()(
dz
dx
z
xzx
dxехdxexxdxxxfXM
хx
.
)(
)(
)1(
)(
1
)(
)(
0
1
0
λ
α
=
αΓλ
αΓα
=+α
αΓλ
=
λαΓ
λ
=
λ
⎟
⎠
⎞
⎜
⎝
⎛
λαΓ
λ
=
∫∫
∞
−α
+α
α
−
α
∞
α
Гdzez
dz
e
z
zz
λ
α
=
)( XM . (281)
2.
∫∫∫
∞∞
λ−+α
α
∞
λ−−α
α
=
αΓ
λ
=
αΓ
λ
==
00
1
0
1222
)()(
)()( dxехdxexxdxxfxXM
хx
= | здійснивши таку саму заміну, як і для визначення М (Х), дістанемо | =
=+αΓ
αΓλ
=
αΓλ
λ
=
λ
⎟
⎠
⎞
⎜
⎝
⎛
λαΓ
λ
=
∫∫
∞
−+α
+α
α
−
+α
∞
α
)2(
)(
1
)(
)(
2
0
1
2
1
0
dzez
dz
e
z
zz
22
)1(
)(
)()1(
λ
+αα
=
αΓλ
αΓα+α
=
;
.
)1(
)()()(
22
22
2
2
22
λ
α
=
λ
α−α+α
=
⎟
⎠
⎞
⎜
⎝
⎛
λ
α
−
λ
+αα
=−= XMXMXD
2
)(
λ
α
=XD
. (282)
3.
.)(
λ
α
=σ X (283)
6. Розподіл Ерланга k-го порядку
Якщо в гамма-розподілі k набуває лише цілих значень (k
≥
1), то
гамма-розподіл перетворюється в розподіл Ерланга k-го порядку,
щільність ймовірностей якої
⎪
⎩
⎪
⎨
⎧
=>λ
−
λ
≤
=
λ−−
.,...3,2,1,0,)(
)!1(
;0,0
)(
1
kxex
n
x
xf
xk
(283а)
Функція розподілу ймовірностей
⎪
⎩
⎪
⎨
⎧
>λ
−
λ
≤
=
∫
λ−−
.0,)(
)!1(
;0,0
)(
0
1
xex
k
x
xF
x
xn
(283б)
246
Закону розподілу Ерланга k-го порядку підлягає сума незалежних
випадкових величин х = х
1
+ х
2
+ … + х
к
, кожна з яких має експонен-
ціальний закон із параметром
λ
.
6.1. Числові характеристики
.)(.3
;)(.2
;)(.1
2
λ
=σ
λ
=
λ
=
k
X
k
XD
k
XM
(283в)
Приклад 8. Задано
⎪
⎩
⎪
⎨
⎧
>
<
=
−
.0,
;0,0
)(
2
1
5
xeCx
x
xf
x
Знайти С і F(x). Обчислити М (Х), D (Х), σ(Х).
Розв’язання. Із умови задачі маємо:
.
2
1
,6 =λ=α
Використовуючи формули (275), (276), (277), (281), (282), (283), за-
писуємо:
7680
1
12064
1
5164
1
)6(
2
1
)(
6
=
⋅
=
⋅
=
Γ
⎟
⎠
⎞
⎜
⎝
⎛
=
αΓ
λ
=
α
C
.
Тоді
⎪
⎩
⎪
⎨
⎧
≥
<
=
⎪
⎩
⎪
⎨
⎧
>
<
=
∫
−
−
x
x
x
xdxex
x
xF
xex
x
xf
0
2
1
5
2
1
5
.0,
7680
1
;0,0
)(
;0,
7680
1
;0,0
)(
;12
2
1
6
)( ==
λ
α
=XM
;24
4
1
6
)(
2
==
λ
α
=XD
.9,424)( ≈=σ X
247
7. Експоненціальний закон розподілу
Експоненціальним законом випадкової величини називають гам-
ма-розподіл, в якому
α
= 1.
Для цього закону розподілу
⎪
⎩
⎪
⎨
⎧
>λ
<
=
λ−
;0,
;0,0
)(
xe
x
xf
x
(284)
⎪
⎩
⎪
⎨
⎧
≥−
<
=
λ−
.0,1
;0,0
)(
xe
x
xF
x
(285)
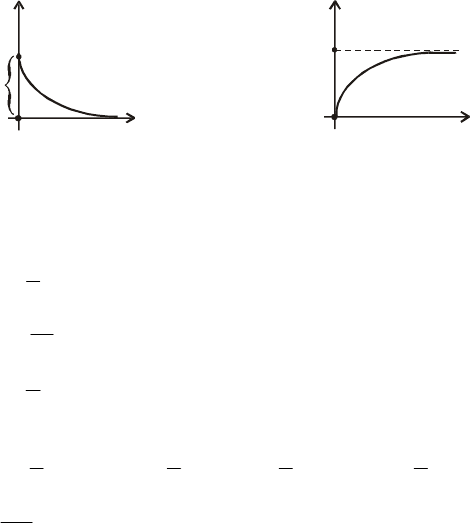
Графіки f (x), F(x) зображені на рис. 102 і 103.
0
x
fx
()
λ
0
x
Fx
()
1
Рис. 102 Рис. 103
7.1. Числові характеристики
Оскільки
α
= 1, маємо такі співвідношення.
1.
.
1
)(
λ
=XM
(286)
2.
2
1
)(
λ
=XD
. (287)
3.
λ
=σ
1
)( X
. (288)
4. Me для експоненціального закону визначається так:
.
2ln
Me
.2ln
2
1
lnMe
2
1
2
1
1
2
1
)Me(
MeMe
λ
=
−==λ−→=→=−→=
λ−λ−
eeF
(289)
Серед усіх законів неперервних випадкових величин лише експо-
ненціальному притаманна властивість — відсутність післядії, а саме:
якщо пов’язати випадкову величину із часом, то для цього закону ми-
нуле не впливає на передбачення подій у майбутньому. Цю власти-
вість експоненціального закону використовують у марківських випа-
дкових процесах, теорії масового обслуговування,
теорії надійності.

248
Властивість відсутності післядії унаочнює рис. 104.
(
)
0
tt
e
−
λ
−
λ
ft
()
λ
0
tt
0
0
tt
e
−
λ
−
Рис. 104
На рис. 104 зображено щільність експоненціального закону .
t
e
λ−
λ
Коли збіжить час t
0
, який вигляд матиме щільність експоненціально-
го закону на проміжку[t
0
,
∞
]?
Розглянемо заштриховану область. Щоб звести заштриховану
область до стандартного для щільності вигляду, маємо виконати та-
ке нормування, щоб площа, обмежена f (t) на проміжку [t
0
,
∞
], дорі-
внювала одиниці. Дістанемо нову щільність імовірностей, визначену
для t
∈
[t
0
,
∞
], яка буде точною копією початкової функції.
Приклад 9. Задано
⎪
⎩
⎪
⎨
⎧
>−
≤
=
−
.0,1
;0,0
)(
5
xe
x
xF
x
Визначити М (Х), σ (Х), Ме.
Розв’язання. Використовуючи формули (286—289), одержимо:
,
5
11
)( =
λ
=XM
оскільки 5
=
λ
;
.
5
2ln
Me;
5
1
)(;
25
11
)(
2
==σ=
λ
= XXD
8. Бета-розподіл
Неперервна випадкова величина Х має бета-розподіл, якщо
⎪
⎩
⎪
⎨
⎧
>
≤<−
≤
=
−γ−β
.1,0
;10,)1(
;0,0
)(
11
x
xxCx
x
xf
