Жлуктенко В. І., Наконечний С. І. Теорія ймовірностей і математична статистика: У 2 ч. - Ч. І. Теорія ймовірностей
Подождите немного. Документ загружается.

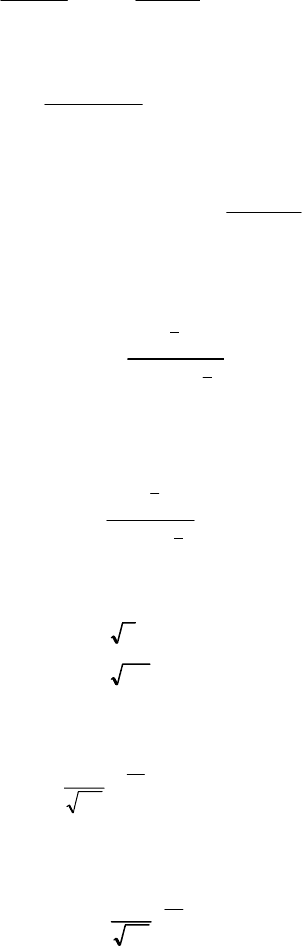
209
Відповідь:
)1(
1
1
+α
β
=
+α
Г
C
,
)1(
1
2
+β
β
=
+γ
Г
C
;
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<
+γ+α
β
≤
=
β−+γ+β
+γ+α
.1,0
;10,
)2(Г
;0,0
1
2
z
zez
z
zf
z
13. Визначити f (y), якщо Y = x
n
і
()
.
)1(
1
2
x
xf
+π
=
Відповідь.
1) для непарного n
()
;
)1(
2
1
1
n
n
yn
y
yf
+π
=
−
2)
для парного n
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
+π
≤
=
−
.0,
)1(
2
;0,0
2
1
1
y
yn
y
y
yf
n
n
14. Випадкова величина Y задана у вигляді
⎪
⎩
⎪
⎨
⎧
<−
≥
=
.0,
;0,
xx
xx
Y
Знайти f (y), якщо щільність імовірностей випадкової величи-
ни Х:
()
.,
2
1
2
2
∞<<∞−
π
=
−
xexf
x
Відповідь.
()
⎪
⎩
⎪
⎨
⎧
>
π
≤
=
.0,
2
4
;0,0
2
4
ye
y
y
yf
y
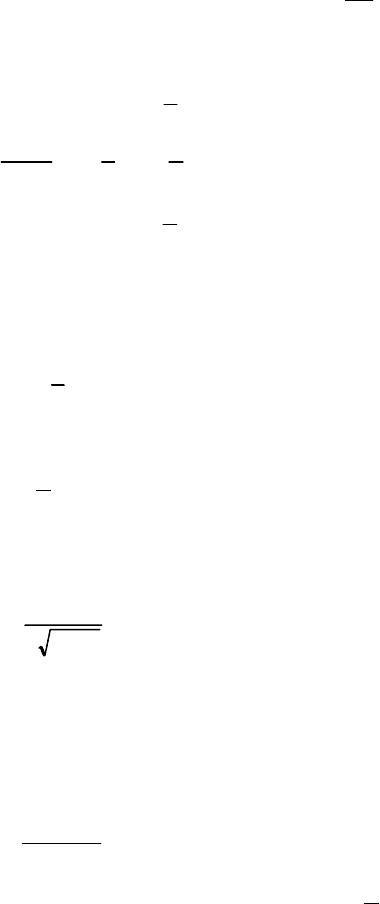
210
15. Випадкова величина Х рівномірно розподілена на проміж-
ку
[]
1;0 і пов’язана із Y функціональною залежністю
x
e
Y
=
π
2
tg
.
Знайти f (y).
Відповідь.
()
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
π
>
π
≤<
π
π
≤
=
.
2
,0
;
2
2
1
,
sin
;
2
1
,0
ey
ey
y
y
yf
arctg
arctg
16. Випадкова величина Х має закон розподілу ймовірностей, що
задано щільністю ймовірністей
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−
−≤
=
.3,0
;33,
6
1
;3,0
x
x
x
xf
Знайти f (y), якщо
xY
6
sin
π
= . Обчислити M (Y), D (Y).
Відповідь.
()
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
≥
≤<−
−π
−<
=
.1,0
;11,
1
1
;1,0
2
y
y
y
y
yf
M (Y) = 0,
D (Y) = 0,5
17. Щільність імовірностей випадкової величини
()
∞<<∞−
+π
= x
x
xf ,
)1(
1
2
.
Знайти f (y), якщо: 1) y =1 – x
3
; 2) y = x
2
; 3) y = arctg x; 4) .
1
x
y =
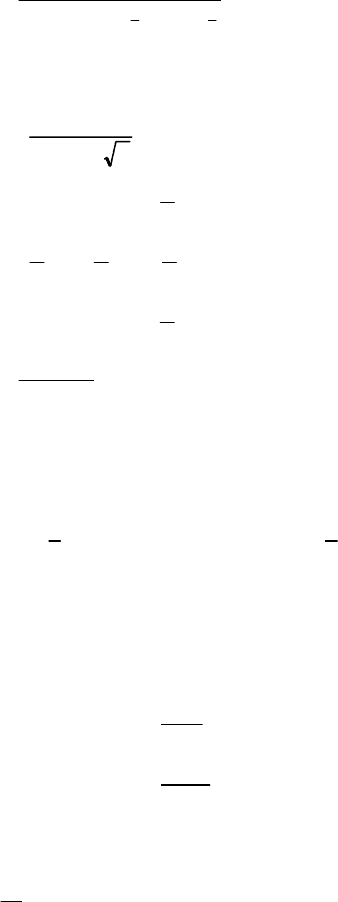
211
Відповідь.
1)
()
;,
)1()1(13
1
3
2
3
2
∞<<∞−
−
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−+π
= y
yy
yf
2)
()
⎪
⎩
⎪
⎨
⎧
≥
+π
<
=
;0,
)1(
1
;0,0
y
yy
y
yf
3)
()
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
π
>
π
≤<
π
−
π
π
−<
=
;
2
,0
;
22
,
1
;
2
,0
y
y
y
yf
4)
()
.,
)1(
1
2
∞<<∞−
+π
= y
y
yf
18. Закони розподілу незалежних випадкових величин Х і Y зада-
ні щільностями ймовірностей:
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−
−≤
=
;4,0
;44,
8
1
;4,0
x
x
x
xf
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−
−≤
=
.6,0
;62,
8
1
;2,0
y
y
y
yf
Знайти f (z), M (z), D (z), якщо Z = Х + Y.
Відповідь.
()
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎨
⎧
>
≤<
−
≤<−
+
−≤
=
;10,0
;102,
64
10
;26,
64
6
;6,0
z
z
z
z
z
z
zf
M (Z) = 0,
()
.
16
17
=ZD

212
19. Задано
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−−
−≤
=
.1,0
;11),1(
4
3
;1,0
2
x
xx
x
xf
Знайти М (Y), якщо Y = min (X; 0,5).
Відповідь. М (Y) = 0.
20. Задано
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−−
−≤
=
.1,0
;11),1(
4
3
;1,0
2
x
xx
x
xf
Знайти М (Y), якщо Y = max (X; 0,5),
Відповідь. М (Y) = 0.
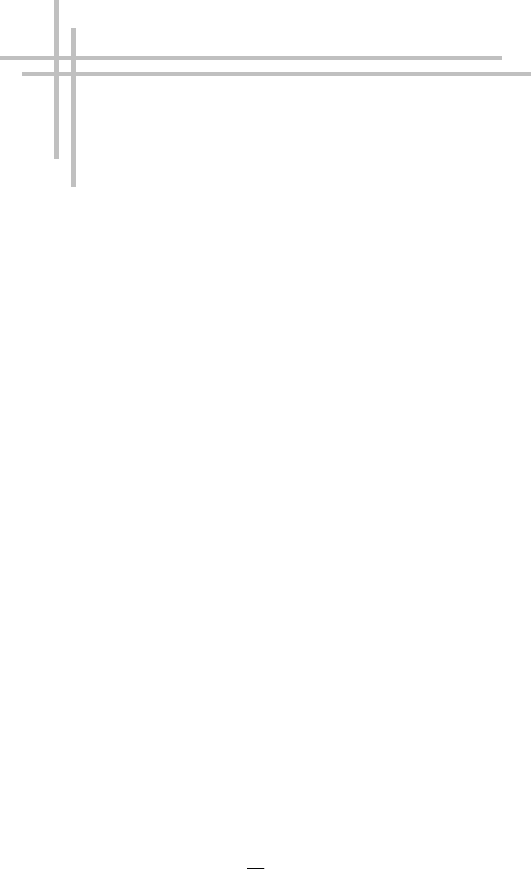
213
РОЗДІЛ IІІ
ОСНОВНІ ЗАКОНИ
РОЗПОДІЛУ
ТЕМА 9. ОСНОВНІ ЗАКОНИ ЦІЛОЧИСЛОВИХ
ВИПАДКОВИХ ВЕЛИЧИН
Серед дискретних випадкових величин особливе місце в
теорії ймовірностей посідають такі, що набувають лише цілих не-
від’ємних значень Х = х
k
= 0, 1, 2, 3, ... .
Ці випадкові величини називають цілочисловими.
1. Імовірнісні твірні функції та їх властивості
Для дослідження законів розподілу цілочислових випадкових ве-
личин використовують імовірнісну твірну функцію. Імовірнісною
твірною функцією називають збіжний степеневий ряд виду:
KK ++++++==
∑
∞
=
mmk
k
k
рхрхрххрррххА
3
3
2
2
10
0
)(
. (231)
Тут р
k
= Р(Х = k), тобто є ймовірність того, що випадкова вели-
чина Х набуде значення k = 0, 1, 2, 3, … .
Імовірнісній твірний функції притаманні такі властивості
1. А(Х) визначена в кожній точці інтервалу [–1; 1].
2. При Х = 1 маємо:
1)1(
0
==
∑
∞
=k
k
рА
,
оскільки це є умовою нормування для дискретної випадкової ве-
личини.
3. Із (231) дістаємо
)0(
!
1
)(k
k
А
k
Р =
,
де А
k
(0) — k-та похідна від А(х), при Х = 0. Отже, знаючи аналі-
тичний вираз для А(х), можемо знайти ймовірність будь-якого мож-
ливого значення Х = k.

214
4.
k
k
k
k
k
k
рkхрххА
∑∑
∞
=
−
∞
=
==
′
0
1
0
)()(
.
При х = 1 дістанемо
()
XМрхkрА
k
k
k
k
k
===
′
∑∑
∞
=
∞
=
00
)1(
.
Звідси
)1()( АXМ
′
=
. (232)
5.
k
k
k
k
k
k
рхkkрkхХА
∑∑
∞
=
−
∞
=
−
−=
′
=
′′
1
2
1
1
)1()()(
.
При х = 1
.)1(()1(
00
2
1
∑∑∑
∞
=
∞
=
∞
=
−=−=
′′
kk
kkk
k
kррkрkkА
Це можна записати так:
).1()1()()1()()1(
22
ААXМАXМА
′
+
′′
=→
′
−=
′′
Тоді
.))1(()1()1()()()(
222
AAAXMXMXD
′
−
′
+
′′
=−=
Отже, формула для обчислення дисперсії буде така:
.))1(()1()1()(
2
AAAXD
′
−
′
+
′′
=
(233)
2. Біноміальний закон розподілу ймовірностей
Цілочислова випадкова величина X має біноміальний закон роз-
поділу, якщо ймовірність її можливих значень обчислюється за фо-
рмулою Бернуллі:
,)(
knkk
nk
qpCkXPP
−
=== k = 0, 1, 2, 3, ..., n. (234 а)
У табличній формі цей закон набирає такого вигляду:
kxX
k
==
0 1 2 3 ... n
knkk
nk
qpCkXPP
−
=== )(
n
q
11 −n
n
pqC
222 −n
n
qpC
333 −n
n
qpC
n
р
При перевірці виконання умови нормування використовується фор-
мула біному Ньютона, тому закон розподілу називають біноміальним:
1)(
00
=+==
−
==
∑∑
nknk
n
k
k
n
n
k
k
pqqpCP .
Побудуємо ймовірнісну твірну функцію для цього закону
nknk
n
k
k
n
knkk
n
n
k
k
k
n
k
k
pxqqpxCqpCxpxXA )()()(
000
+====
−
=
−
==
∑∑∑
.

215
Отже, імовірнісна твірна функція для біноміального закону
n
pxqXA )()( +=
. (234 b)
Знайдемо основні числові характеристики для цього закону:
1.
[]
[
]
;)()()()1()(
1
1
1
nppqnp
'
pxqnp
'
pxqAXM
Х
n
Х
n
=+=+=+=
′
=
=
−
=
)1(
=
+
qp ,
npXM
=
)(
. (235)
2.
[]
[
]
=+−=+=
′′
=
−
=
−
'
ppxqnn
'
pxqnpA
Х
n
Х
n
1
22
1
1
)()1()()1(
=+−=
2
)()1( ppqnn
2
)1( pnn −
;
2
)1()1( pnnA −=
′′
;
;)1()()()(
)()()1())1(()1()(
22222
22222
npqpnpnpnpnpnpnpnpnpnp
npnpnpnppnnAAAXD
=−=+−=−+−=−+
+−=−+−=
′
−
′
+
′′
=
npqXD
=
)( ; (236)
npqX =σ )( . (237)
Приклад 1. У партії однотипних деталей стандартні станов-
лять 95%. Навмання з партії беруть 400 деталей. Визначити
М (Х), D (X), σ (Х) для дискретної випадкової величини Х —
появи числа стандартних деталей серед 400 навмання взятих.
Розв’язання. Цілочислова випадкова величина Х має біноміальний
закон розподілу ймовірностей, яка може набувати значення
Х = k = 0, 1, 2, ..., 400.
Імовірності можливих значень обчислюються за формулою Бернул-
лі:
kkk
k
qpCkXPP
−
===
400
400
)( , де р = 0,95 — імовірність появи стан-
дартної деталі, q = 1 – p =1 – 0,95 = 0,05 — імовірність появи нестанда-
ртної деталі.
Згідно з (235), (236), (237), маємо:
npXM
=
)( = 400 ⋅ 0,95 = 380;
npqXD
=
)( = 400 ⋅ 0,95 ⋅ 0,05 = 19;
npqX =)(σ = 19 ≈ 4,36.
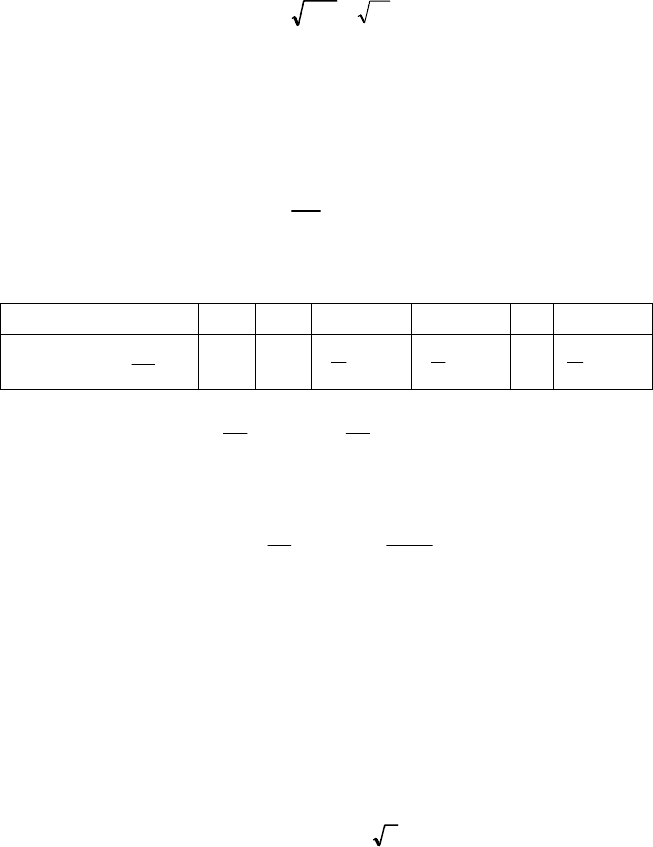
Приклад 2. У кожному із 100 контейнерів міститься по 8 ви-
робів першого сорту, а решта 2 — браковані. Із кожного кон-
тейнера навмання беруть по одному виробу. Визначити М (Х),
D (X), σ (X) для дискретної випадкової величини Х — поява
числа виробів першого сорту серед 100 навмання взятих.
Розв’язання. Цілочислова випадкова величина Х
має біноміальний
закон розподілу. Із умови задачі маємо:
216
n = 100, p = 0,8, q = 0,2, k = 0, 1, 2, 3, ..., 100.
За формулами (235), (236), (237) дістаємо:
npXM
=
)(
= 100 ⋅ 0,8 = 80;
npqXD
=
)(
= 100 ⋅ 0,8 ⋅ 0,2 = 16;
npqX =)(σ
= 16 ≈ 4.
3. Пуассонівський закон
розподілу ймовірностей
Цілочислова випадкова величина Х має пуассонівський закон ро-
зподілу, якщо ймовірності її можливих значень
a
k
k
e
k
a
kXPP
−
===
!
)(
, k = 0, 1, 2 ,3, ..., n, (238)
тобто обчислюється за формулою Пуассона, де
npa
=
. У табличній
формі цей закон розподілу буде такий:
Х = k 0 1 2 3 … n
()
a
k
e
k
a
kXPP
−
===
!
a
e
−
a
ae
−
a
ea
−2
!2
1
a
ea
−3
!3
1
an
ea
n
−
!
1
1
!!
0
00
=====
−
=
−
=
−
∑∑∑
eee
k
a
ee
k
a
P
aa
n
k
k
a
n
k
a
k
k
.
Умова нормування виконується.
Побудуємо ймовірну твірну функцію для цього закону:
)1(
000
)(
!
)(
−−
=
−−
==
=====
∑∑∑
xaaxa
n
k
k
aa
n
k
k
k
k
n
k
k
eee
k
ax
ee
k
a
xpxXA .
Отже,
)1(
)(
−
=
xa
eXA . (239)
Скориставшись (232), (233), дістанемо вирази для М (Х), D (X):
1.
aaeeAXM
X
xa
X
xa
==
′
=
′
=
=
−
=
−
1
)1(
1
)1(
)()()1()( ;
npaXM
=
=
)( . (240)
2.
2
1
)1(2
1
)1(
)()()1( aeaaeA
X
xa
X
xa
==
′
=
′′
=
−
=
−
;
aaaaAAAXD =−+=
′
−
′
+
′′
=
222
))1(()1()1()(
;
aXP =)(
; (241)
aX =σ )( . (242)

217
Отже, для Пуассонівського закону розподілу ймовірностей
М (Х) = D (X) = а.
Приклад 3. Прилад має 1000 мікроелементів, які працюють
незалежно один від одного. Імовірність того, що мікроеле-
мент вийде із ладу під час роботи приладу, є величиною
сталою і дорівнює 0,004. Визначити М (Х), D (X), σ (Х) ви-
падкової величини Х — числа мікроелементів, що вийдуть із
ладу під час роботи приладу.
Розв’язання
. Випадкова величина Х є цілочисловою, що має пуас-
сонівський закон розподілу — імовірності її можливих значень обчис-
люються за формулою Пуассона, котра є асимптотичною щодо форму-
ли Бернуллі для великих значень n і малих значень p, так званих
малоймовірних випадкових подій.
За умовою задачі маємо:
npXM =)(
= 1000 ⋅ 0,004 = 4;
npXMXD
=
=
)()( = 4;
()
.24 ===σ прХ
Приклад 4. У деякому населеному пункті маємо 0,1% даль-
тоніків. Навмання вибирають 5000 мешканців цього населе-
ного пункту. Визначити М (Х), D (X), σ (Х) випадкової вели-
чини Х — числа дальтоніків, яких буде виявлено серед 5000
навмання вибраних мешканців.
Розв’язання. Цілочислова випадкова величина Х має пуассонівсь-
кий закон розподілу. Із умови задачі:
n = 5000, p = 0,0001. Згідно з
(240), (241), (242), дістаємо:
npXM
=
)( = 5000 ⋅ 0,0001 = 0,5;
npXMXD
=
=
)()( = 0,5;
71,05,0)( ≈==σ npX
.
4. Геометричний закон розподілу ймовірностей
Інколи спроби здійснюють до першої появи випадкової події.
Число проведених спроб буде цілочисловою випадковою величи-
ною. Цілочислова випадкова величина Х має геометричний закон
розподілу, якщо ймовірності її можливих значень
1
)(
−
===
k
k
pqkXPP
, k = 1, 2, 3, …, n. (243)
Тут p — імовірність появи випадкової події в кожній спробі — є
величиною сталою, q = 1 – p.

218
У табличній формі геометричний закон розподілу такий:
kХХ
k
==
1 2 3 4 ...
1
)(
−
===
k
k
pqkXPP
p
pq
2
pq
3
pq
...
При перевірці умови нормування використовується формула су-
ми нескінченної геометричної прогресії, тому й закон розподілу на-
зивають геометричним:
.1
1
1
1
...)1(...
3232
1
==
−
=++++=++++=
∑
∞
=
p
p
q
pqqqppqpqpqpP
k
k
Побудуємо ймовірнісну твірну функцію
∑∑∑
∞
=
−
∞
=
∞
=
===
1
1
11
)()(
k
kk
k
k
k
k
k
qx
q
p
pqxpxXA
.
Ураховуючи, що
1≤Х
, дістаємо
() ()
.
1
1
11
k
k
k
k
k
k
k
k
qx
q
p
pqxpxХА
∑∑∑
∞
=
−
∞
=
∞
=
===
Оскільки
1≤X , то
qx
qx
q
p
qxqxqx
q
p
qx
q
p
XA
k
k
−
=+++==
∑
∞
=
1
...))()(()()(
32
1
;
qx
px
XA
−
=
1
)(
. (244)
Числові характеристики для цього закону:
1.
=
⎥
⎦
⎤
⎢
⎣
⎡
−
+−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
′
=
== 1
2
1
)1(
)1(
1
)1()(
ХХ
qx
pqxqxp
'
qx
px
AXM
p
p
p
q
p
qx
p
X
1
)1()1(
22
1
2
==
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
=
;
p
XM
1
)( =
. (245)
2.
=
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
′′
=
=
1
4
1
2
)1(
)1(2
)1(
)1(
Х
Х
qx
qxpq
'
qx
p
A
233
1
3
22
)1(
2
)1(
2
p
q
p
pq
qx
pq
qx
pq
X
==
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
=
;
2222
2
12112
))1(()1()1()(
p
q
p
pq
p
p
p
q
AAAXD =
−
+
=−+=
′
−
′
+
′′
=
.
