Жлуктенко В. І., Наконечний С. І. Теорія ймовірностей і математична статистика: У 2 ч. - Ч. І. Теорія ймовірностей
Подождите немного. Документ загружается.

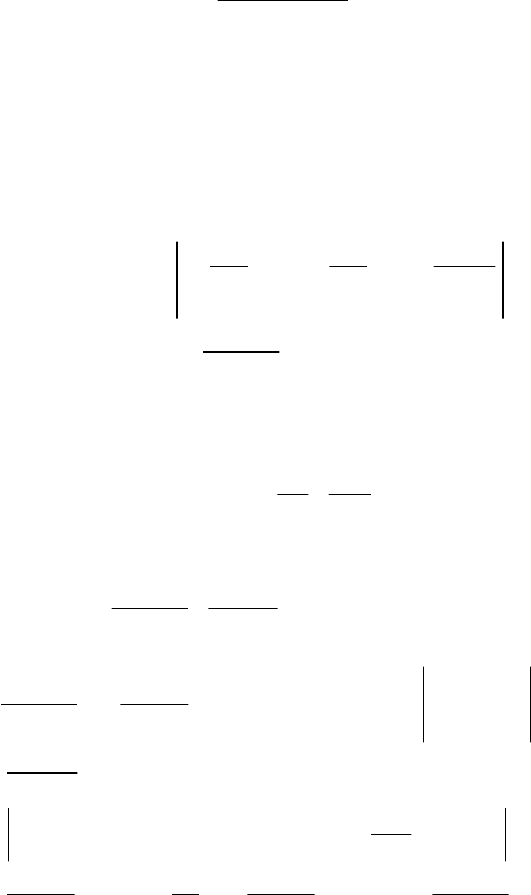
249
Для визначення С використовуємо умову нормування
∫
−γ−β
−
=
1
0
11
)1(
1
dxxx
C
.
Інтеграл
∫
−γ−β
−
1
0
11
)1( dxxx
називають бета-функцією і позначають
);(
γ
βB
, де
.0,0 >
γ
>β
Тобто:
∫
−γ−β
−=γβ
1
0
11
)1();( dxxxB
. (290)
Отже, знайдемо
).;(
γ
β
B
()
()
=
∞<<→<<
+
=
+
=−
+
=
=−
−γ
−β
∫
zx
z
dz
dx
z
x
z
z
x
dxхх
010
1
;
1
1
1;
1
1
2
1
1
0
1
()
dz
z
z
∫
∞
γ+β
−β
+
=
0
1
1
. (290а)
Як відомо,
∫
∞
−−
=Γ
0
1
.)( dtetP
tp
Якщо t = my, то
()
()
.
11
0
1
0
1
dyеу
Р
m
dyеутР
тур
p
турр
∫∫
∞
−−−
∞
−
Γ
=→=Γ
Позначимо
γ
+
β
=
+= pzm ),1(
.
Тоді
∫
∞
+−−γ+
γ+β
γ+βΓ
=
+
0
)1(1
)(
1
)1(
1
dyey
z
yzp
. (291)
Підставляючи вираз (291) у (290а), дістаємо
=
⎟
⎠
⎞
⎜
⎝
⎛
γ+β
=
==
⎟
⎠
⎞
⎜
⎝
⎛
γ+βΓ
=
+
−−γ+β
∞∞
−−β
−β
∞∞
+−−γ+β
γ+β
−β
∫∫
∫∫∫
dyeydzez
Г
dzzdyeydz
z
z
yyz
yz
1
00
1
1
00
)1(1
1
0
1
)(
1
)(
1
)1(
няінтегруван
порядок
поміняємо
=
βΓ
==
∫
∞
β
−−β
дістаємоінтеграл внутрішній оскільки
,
)(
0
1
y
dzez
yz
)(
)()(
)(Г
)(Г
1
)(
)(
0
1
0
1
γ+βΓ
γΓβΓ
=
γ+β
β
=
γ+βΓ
βΓ
=
∫∫
∞
−−γ
∞
β
−−γ+β
dyеуdy
у
еу
уу
.
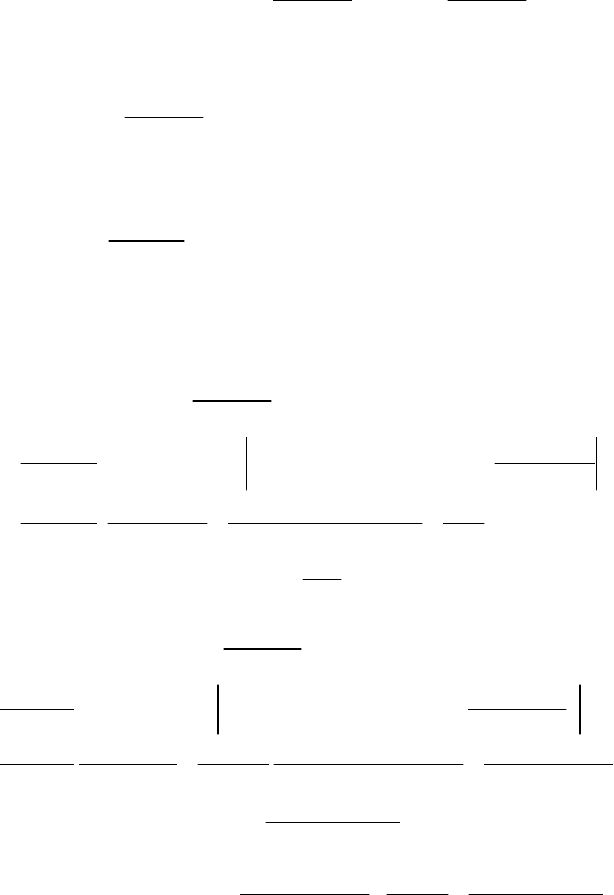
250
Остаточно маємо:
,
)(
)()(
)1(),(
1
0
11
∫
γ+βΓ
γΓβΓ
=−=γβ
−γ−β
dxxxB тоді
)()(
)(
γΓβΓ
γ+βΓ
=С
. (292)
Отже,
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−
γΓβΓ
γ+βΓ
≤
=
−γ−β
.1,0
;10,)1(
)()(
)(
;0,0
)(
11
x
xxx
x
xf
(293)
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−
γβΓ
γ+βΓ
≤
=
∫
−γ−β
.1,1
;10,)1(
)(Г)(
)(
;0,0
)(
0
11
x
xdxхх
x
xF
х
(294)
8.1. Числові характеристики
1.
∫∫
=−
γβΓ
γ+βΓ
==
−γ−β
1
0
11
1
0
)1(
)()(
)(
)()( dxххх
Г
dxxxfXM
.
)()()(Г)(
)()()(
)1(
)(Г)1(
)()(
)(
)1(
)()1(
);1()1()1(
)()(
)(
1
0
1
1
0
1
γ+β
β
=
γ+βΓγ+βγβΓ
γΓβΓβγ+βΓ
=
+γ+βΓ
γ+βΓ
γΓβΓ
γ+βΓ
=
=
+γ+βΓ
γΓ+βΓ
=γ+β=−=−
γΓβΓ
γ+βΓ
=
∫∫
−γβ−γβ
Вdxххdxхх
.)(
γ+β
β
=XM
(295)
2.
∫∫
=−
ςβΓ
γ+βΓ
==
−γ−β
1
0
112
1
0
22
)1(
)()(
)(
)()( dxххх
Г
dxxfxXM
.
)()1(
)1(
)()()1(
)()()1(
)()(
)(
)2(
)()2(
)()(
)(
)2(
)()2(
);2()1()1(
)()(
)(
1
0
11
1
0
11
γ+β+γ+β
β+β
=
γ+βΓγ+β+γ+β
γΓβΓβ+β
γΓβΓ
γ+βΓ
=
+γ+βΓ
γΓ+βΓ
γβΓ
γ+βΓ
=
=
+γ+βΓ
γΓ+βΓ
=γ+β=−=−
γβΓ
γ+βΓ
=
∫∫
−γ+β−γ+β
Г
Bdxххdxхх
Г
()
(
)
()( )
1
1
2
+γ+βγ+β
+ββ
=ХМ
;
3.
.
)1()()()1()(
)1(
)()()(
22
2
22
+γ+βγ+β
βγ
=
γ+β
β
−
+γ+βγ+β
+ββ
=−= XMXMXD
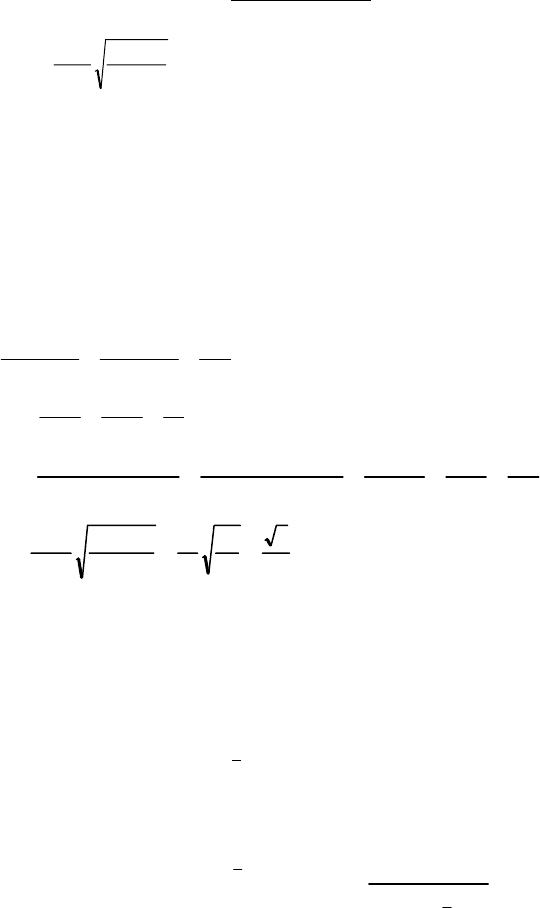
251
()
()( )
.
1
2
+γ+βγ+β
βγ
=XD
(296)
4.
1
1
)(
+γ+β
βγ
γ+β
=σ X
. (297)
Приклад 10. Задано
⎪
⎩
⎪
⎨
⎧
>
≤<−
≤
=
.1,0
;10,)1(
;0,0
)(
65
x
xxCx
x
xf
Знайти С, М (Х), D (Х), σ (Х).
Розв’язання. Використовуючи формули (292), (295), (296), (297):
;
13
6
76
6
)(
;554478911
!6!5
!12
)7()6(
)13(
)()(
)(
=
+
=
γ+β
β
=
=⋅⋅⋅==
ΓΓ
Γ
=
γΓβΓ
γ+βΓ
=
XM
C
;
169
3
1183
21
1413
42
)176()76(
76
)1()(
)(
222
==
⋅
=
+++
⋅
=
+γ+βγ+β
βγ
=XD
.
13
3
14
42
13
1
1
1
)( ==
+γ+β
βγ
γ+β
=σ X
9. Розподіл Вейбулла
Неперервна випадкова величина Х має розподіл Вейбулла, якщо
⎪
⎩
⎪
⎨
⎧
>θ>β>
<
=
β
⎟
⎠
⎞
⎜
⎝
⎛
θ
−
−β
.0,0,0,
;0,0
)(
1
xeCx
x
xf
x
За умовою нормування визначимо сталу С:
.
1
11)(
00
0
1
1
∫∫
∫
∞∞
∞
⎟
⎠
⎞
⎜
⎝
⎛
θ
−
−β
⎟
⎠
⎞
⎜
⎝
⎛
θ
−
−β
β
β
=→=→=
dxex
CdxeCxdxxf
x
x

252
()
.
0
0
1
0
1
1
1
1
0
1
β
θ
=−
β
θ
=
=
β
θ
=
β
θ
θ=
β
θ
=
→θ=→=
⎟
⎠
⎞
⎜
⎝
⎛
θ
=
β
∞
−
β
∞
−
β
β
β−
∞
−
β
−β
−β
β
β−
β
β
∞
⎟
⎠
⎞
⎜
⎝
⎛
θ
−
−β
∫∫∫
β
z
zz
x
e
dzedzzez
dzzdx
zxz
x
dxex
.
β
θ
β
=C
(298)
Щільність імовірностей для розподілу Вейбулла:
()
⎪
⎩
⎪
⎨
⎧
>
⎟
⎠
⎞
⎜
⎝
⎛
θθ
β
<
=
⎟
⎠
⎞
⎜
⎝
⎛
θ
−
−β
.0,
;0,0
1
xe
x
x
xf
p
x
(299)
Функція розподілу ймовірностей
.1)()(
0
0
1
00
ββββ
⎟
⎠
⎞
⎜
⎝
⎛
θ
−
⎟
⎠
⎞
⎜
⎝
⎛
θ
−
β
⎟
⎠
⎞
⎜
⎝
⎛
θ
−
⎟
⎠
⎞
⎜
⎝
⎛
θ
−
−β
−=−=
⎟
⎠
⎞
⎜
⎝
⎛
θ
=
⎟
⎠
⎞
⎜
⎝
⎛
θθ
β
==
∫∫∫
x
x
x
x
xx
xx
ee
x
dedxe
x
dxxfxF
Звідси
⎪
⎩
⎪
⎨
⎧
>−
≤
=
β
⎟
⎠
⎞
⎜
⎝
⎛
θ
−
0,1
;0,0
)(
xe
x
xF
x
(300)
Отже, розподіл Вейбулла визначається двома параметрами β, θ.
9.1. Числові характеристики
1.
=
⎟
⎠
⎞
⎜
⎝
⎛
θ
β=
⎟
⎠
⎞
⎜
⎝
⎛
θθ
β
==
ββ
⎟
⎠
⎞
⎜
⎝
⎛
θ
−
β
∞
⎟
⎠
⎞
⎜
⎝
⎛
θ
−
−β
∞∞
∫∫∫
dxe
x
dxe
x
xdxxxfXM
xx
0
1
00
)()(
);1
1
(
00
1
1
1
1
1
1
+
β
Γθ=θ=
β
θ
β=
β
θ
=→
→=
θ
→=
⎟
⎠
⎞
⎜
⎝
⎛
θ
=
−
∞∞
β
−
β
−
−
β
β
β
∫∫
dzezdzzze
dzz
x
dx
z
x
z
x
zz
()
.1
1
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
β
Γθ=XM
(301)

253
2.
=
⎟
⎠
⎞
⎜
⎝
⎛
θ
βθ=
⎟
⎠
⎞
⎜
⎝
⎛
θθ
β
==
ββ
⎟
⎠
⎞
⎜
⎝
⎛
θ
−
+β
∞
⎟
⎠
⎞
⎜
⎝
⎛
θ
−
−β
∞∞
∫∫∫
dxe
x
dxe
x
xdxxfxXM
xx
1
0
1
00
222
)()(
);1
2
(
2
0
2
2
0
1
1
1
1
дістанемо),(визначенніприі
якзаміну,самутакузробивши
+
β
Γθ=θ=
=
β
θ
θβ==
−
∞
β
∞
−
β
−
+
β
∫
∫
dtet
dttet
t
t
XM
()
⎟
⎠
⎞
⎜
⎝
⎛
+
β
θ= 1
2
Г
2
ХМ
.
3.
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
+
β
−
⎟
⎠
⎞
⎜
⎝
⎛
+
β
θ= 1
1
Г1
2
Г)(
22
XD . (302)
4.
⎟
⎠
⎞
⎜
⎝
⎛
+
β
Γ−
⎟
⎠
⎞
⎜
⎝
⎛
β
Γ
θ=σ
1
12
)(
2
X
. (303)
Приклад 11. За заданими параметрами β = 2, θ = 4 записати
математичний вираз для f (x), F (x) і обчислити числові харак-
теристики М (X), D (X), σ (X).
Розв’язання. Використовуючи (302) — (306),
⎪
⎩
⎪
⎨
⎧
>
≤
=
−
.0,
8
1
;0,0
)(
16
1
xxe
x
xf
x
1.
=)(XM
π=
⎟
⎠
⎞
⎜
⎝
⎛
Γ=
⎟
⎠
⎞
⎜
⎝
⎛
+Γ=
⎟
⎠
⎞
⎜
⎝
⎛
+
β
Γθ 2
2
1
2
1
41
2
1
41
1
;
,
2
1
π=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
що було нами доведено;
2.
=
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
+Γ−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
+
β
Γ−
⎟
⎠
⎞
⎜
⎝
⎛
+
β
Γθ= 1
2
1
)2(Г161
1
1
2
)(
222
XD
).8(4
4
1
216 π−=
⎥
⎦
⎤
⎢
⎣
⎡
π−=
3.
π−=σ 82)(
X .

254
10. Закони розподілу випадкових величин,
пов’язаних із нормальним законом розподілу
Нормальному закону розподілу належить центральне місце в по-
будові статистичних моделей у теорії надійності та математичній
статистиці.
10.1. Розподіл
χ
2
(хі-квадрат)
Якщо кожна із X
і
(і = 1, 2, …, k) незалежних випадкових величин
характеризується нормованим законом розподілу ймовірностей
))1;0((
N , то випадкова величина
∑
=
=
k
i
i
XX
1
2
матиме розподіл χ
2
із k
ступенями свободи, щільність імовірностей якої буде
⎪
⎩
⎪
⎨
⎧
≥
>
=
−−
.0,
;0,0
)(
2
1
2
xeCx
x
xf
xk
Використовуючи умову нормування, знаходимо
dxeх
С
xk
2
0
1
2
1
−
∞
−
∫
=
;
∫∫∫
∞∞
−
−
−
−
∞
−−
⎟
⎠
⎞
⎜
⎝
⎛
Γ===
=
=→=
=
00
2
1
22
1
2
0
2
1
2
.
2
222)2(
2
2
2
k
dzezdzez
dzdx
zxz
x
dxex
k
z
kk
z
kxk
Тоді
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
2
2
1
2
k
C
k
(304)
Отже,
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
⎟
⎠
⎞
⎜
⎝
⎛
Γ
≤
=
−−
.0,
2
2
1
;0,0
)(
2
1
2
2
xex
k
x
xf
xk
k
(305)
Функція розподілу ймовірностей
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
⎟
⎠
⎞
⎜
⎝
⎛
Γ
≤
=
∫
−−
.0,
2
2
1
;0,0
)(
0
2
1
2
2
xdxex
k
x
xF
x
xk
k
(306)
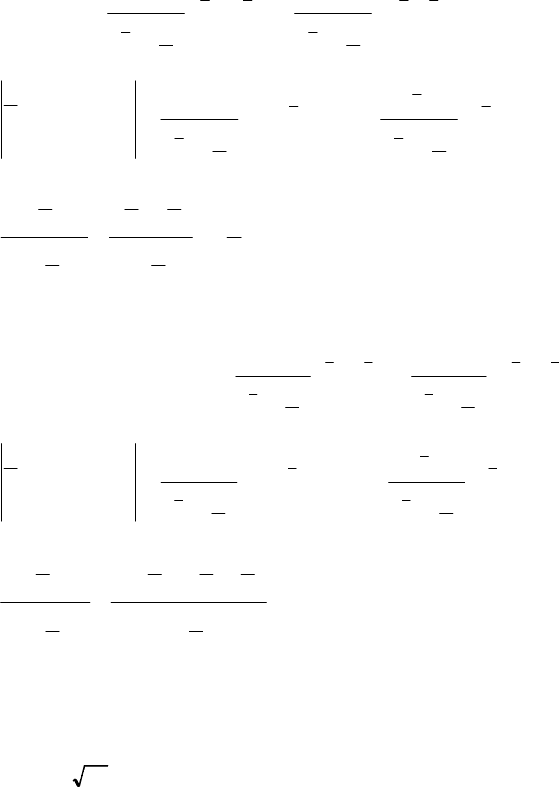
255
10.1.1. Числові характеристики
1.
()
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
−
∞∞
−−
∫∫
dxex
k
dxex
k
xXM
xk
k
xk
k
2
00
2
2
2
1
2
2
2
2
1
2
2
1
=
=
=→=
=
dzdx
zxz
x
2
;2
2
∫∫
∞
−
∞
+
−
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
0
2
0
2
1
2
2
2
2
2
2
2)2(
2
2
1
dzez
k
dzez
k
z
k
k
k
z
k
k
= k
k
k
kk
k
k
==
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+Γ
2
2
2
Г
22
2
2
1
2
2
;
kXM
=
)(
. (307)
2.
∫∫∫
∞
−+
∞∞
−−
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
==
0
2
1
2
2
00
2
1
2
2
222
2
2
1
2
2
1
)()( dxex
k
dxex
k
xdxxfxXM
xk
k
xk
k
=
=
=→=
=
dzdx
zxz
x
2
;2
2
∫∫
∞
−
+
∞
+
−
+
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
0
1
2
0
2
2
2
1
2
2
2
2
2
2)2(
2
2
1
dzez
k
dzez
k
z
k
k
k
z
k
k
)2(
2
22
1
2
4
2
2
2
4
+=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+Γ
= kk
k
kkk
k
k
;
)2()(
2
+= kkXM
;
3.
kkkkkkkXMXMXD 22)2()()()(
22222
=−+=−+=−= ;
kXD 2)(
=
. (308)
4.
kX 2)( =σ . (309)
Приклад 12. Кожна з 10 незалежних випадкових величин х
і
має закон розподілу N (0; 1). Записати вирази для f (x), F(x) і
обчислити M (X), D (X), σ (X).
Розв’язання. Використовуючи (308)—(312), дістаємо:
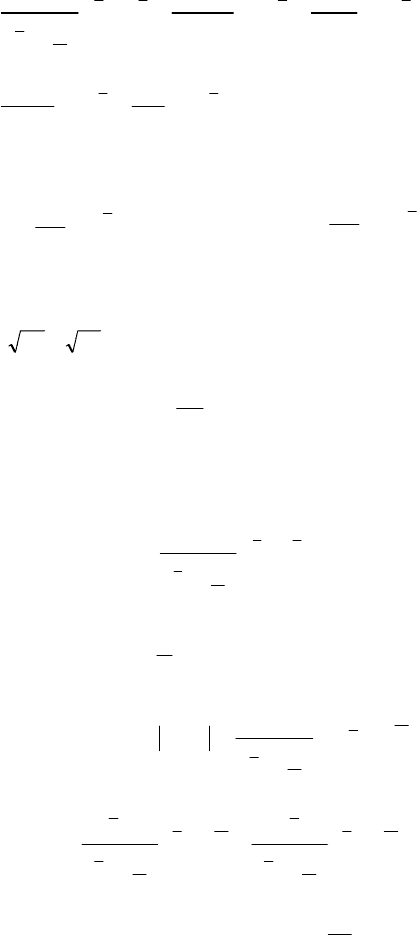
256
()
.
768
1
2432
1
!432
1
52
1
2
2
1
)(
2
4
2
4
2
4
2
4
5
2
1
2
2
xx
xxxk
k
exex
exexex
k
xf
−−
−−−−
=
⋅
=
=
⋅
=
Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
Таким чином,
⎪
⎩
⎪
⎨
⎧
>
≤
=
−
;0,
768
1
;0,0
)(
2
4
xex
x
xf
x
⎪
⎩
⎪
⎨
⎧
>
≤
=
∫
∞
−
;0,
768
1
;0,0
)(
0
2
4
xdxex
x
xF
x
.47,4202)(
;202)(
;10)(
≈==σ
==
==
kX
kXD
kXM
10.2. Розподіл
k
2
χ
Нехай випадкова величина Y має розподіл χ
2
із k ступенями
свободи:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
⎟
⎠
⎞
⎜
⎝
⎛
Γ
≤
=
−−
.0,
2
2
1
;0,0
)(
2
1
2
2
yey
k
y
yf
y
k
k
Знайти f (x
),
якщо
k
Y
X =
. Оскільки Y = kХ і при цьому
ky
x
=
′
, то
згідно зі (196) дістанемо
()
=ψ
′
ψ= )()()( xxfxf
()
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
−
−
kekx
k
kx
k
k
2
1
2
2
2
2
1
.
2
2
2
2
2
1
2
2
2
2
1
2
2
1
2
kxk
k
k
kxk
k
k
ex
k
k
ex
k
kk
−−−−
−
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
Отже, щільність імовірностей розподілу
k
2
χ
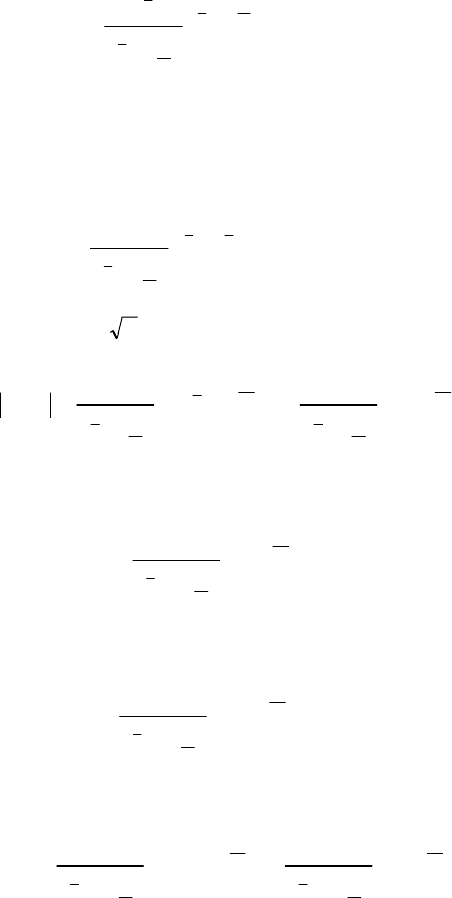
257
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
⎟
⎠
⎞
⎜
⎝
⎛
Γ
≤
=
−−
.0,
2
2
;0,0
)(
2
1
2
2
2
xex
k
k
x
xf
kxk
k
k
(310)
10.3. Розподіл χ
Нехай випадкова величина Y має розподіл χ
2
із k ступенями свободи:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
⎟
⎠
⎞
⎜
⎝
⎛
Γ
≤
=
−−
.0,
2
2
1
;0,0
)(
2
1
2
2
yey
k
y
yf
y
k
k
Знайдемо f (x), якщо
YX =
. Оскільки Y = x
2
= ψ(х), то
xy 2)( =ψ
′
.
Використовуючи (196), дістаємо
()
=ψ
′
ψ= )()()( xxfxf
()
.
2
2
2
2
2
2
1
2
1
2
2
1
2
2
2
22
x
k
k
x
k
k
ex
k
xex
k
−
−
−
−
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
Випадкова величина Х має розподіл χ, якщо
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
⎟
⎠
⎞
⎜
⎝
⎛
Γ
≤
=
−
−
−
.0,
2
2
1
;0,0
)(
2
1
1
2
2
xex
k
x
xf
x
k
k
(311)
Функція розподілу ймовірностей
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
⎟
⎠
⎞
⎜
⎝
⎛
Γ
≤
=
∫
−
−
−
.0,
2
2
1
;0,0
)(
0
2
1
1
2
2
xdxex
k
x
xF
x
x
k
k
(312)
10.3.1. Числові характеристики χ-розподілу
1.
∫∫∫
∞
−
−
∞
−
−
−
∞
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
==
0
2
1
2
0
2
1
1
2
0
22
2
2
1
2
2
1
)()( dxex
k
dxexx
k
dxxxfXM
x
k
k
x
k
k
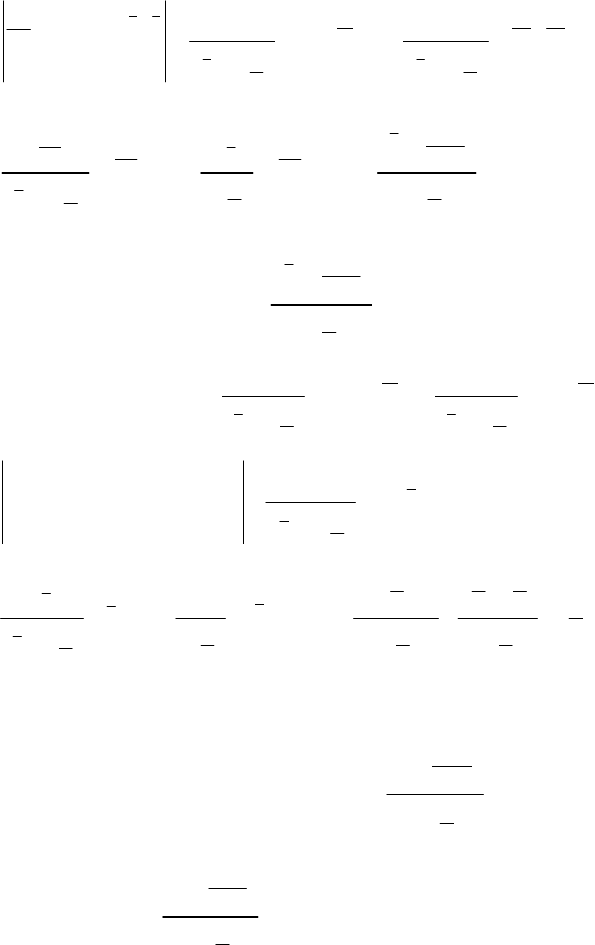
258
=
=
=→=
=
dzxdx
zxz
x
2
2
2
1
2
2
2
∫∫
∞
−
−−
∞
−
−
−
−
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
0
2
1
2
1
0
1
2
2
1
1
2
2
2
2
1
2
2
1
2
dzez
k
xdxex
k
z
kk
k
x
k
k
= ;
2
2
1
2
2
2
2
2
2
2
1
0
1
2
1
2
1
0
2
1
1
2
2
1
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
∫∫
∞
−
−
+
∞
−
−
−
−
k
k
dzez
k
dzez
k
z
k
z
k
k
k
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
=
2
2
1
2
)(
2
1
k
k
xM
. (313)
2.
∫∫∫
∞
−
+
−
∞
−
−
−
∞
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
==
0
2
1
1
2
0
2
12
1
2
0
22
22
2
2
1
2
2
1
)()( dxex
k
dxexx
k
dxxfxXM
x
k
k
x
k
k
∫
∞
−
−
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
==
0
2
1
2
2)2(
2
2
1
дістанемо
),(визначенніприіяк
заміну,самутакузробивши
dzez
k
z
k
k
XМ
k
k
k
kk
k
k
dzez
k
dzez
k
z
k
z
k
k
k
==
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
Γ
=
∫∫
∞
−
−
⎟
⎠
⎞
⎜
⎝
⎛
+
∞
−
−
2
2
2
22
2
2
1
2
2
2
2
2
2
2
0
11
2
0
2
1
2
2
;
kXM =)(
2
; (314)
.
2
2
1
2
)()()(
2
2
22
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
−=−=
k
k
kXMXMXD
3.
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
−=
2
2
1
2
)(
2
2
k
k
kXD
. (315)
