Жлуктенко В. І., Наконечний С. І., Савіна С.С. Теорія ймовірностей і математична статистика: У 2-х ч. - Ч. ІІ. Математична статистика
Подождите немного. Документ загружается.


67
Обчислимо D
B
:
() () () ()
30
7350630052502200
2222
2
+⋅+⋅+⋅+⋅
=
∑
n
nx
ii
() () () ()
=
⋅+⋅+⋅+⋅+
30
1550250024505400
2222
=
30
00040500080050085700054050031200080 +
+
+
+
+
+
3,126583
30
3797500
30
500302000500
==
+
+
.
() ( )
.3,75581190253,1265833453,126583
22
B
2
B
=−=−=−=
∑
x
n
nx
D
ii
Отже,
2
B
]мкв[3,7558=D
.
Виправлена дисперсія і виправлене середнє квадратичне відхилення
дорівнюватимуть:
2
B
2
]мкв[9,78183,7558
29
30
3,7558
130
30
1
=⋅=⋅
−
=
−
= D
n
n
S
;
мкв.42,889,7818
1
B
≈=
−
= D
n
n
S
Оскільки
,01,099,011
=
−
=
γ
−=α
то згідно з (427), (428) знаходи-
мо значення
,
2
1
χ
2
2
χ
, а саме:
()
.995,0005,01
2
01,0
1
2
1
2
1
2
=−=−=
α
−=χ>χP
()
.005,0
2
01,0
2
2
2
2
==
α
=χ>χP
За таблицею (додаток 4) знаходимо:
()
(
)
.3,1429;995,01;995,0
2
1
2
1
==χ=−=χ kmk
(
)
.5,5229;005,0
2
2
==χ k
Обчислимо кінці довірчого інтервалу для
Г
D
:
01431997818
552
291
2
2
2
,,
,
S
χ
n
=⋅=
−
;

68
51585697818
314
291
2
2
1
,,
,
S
χ
n
=⋅=
−
.
Отже, довірчий інтервал для
Г
D
буде таким:
.5,158560,4319
Г
<
<
D
Довірчий інтервал для
Г
σ
становить
.83,1303,68
Г
<
σ
<
Довірчий інтервал для
Г
σ
можна побудувати із заданою на-
дійністю γ, узявши розподіл χ .
Оскільки
(
)
,
Г
γ=δ<−σ SP (429)
то рівність (429) можна записати так:
(
)
γ=δ+<σ<δ− SSP
Г
або
.11
Г
γ=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
δ
+<σ<
⎟
⎠
⎞
⎜
⎝
⎛
δ
−
S
S
S
SP
Позначивши
,q
S
=
δ
дістанемо
(
)
(
)()
γ
=
+
<
σ
<
−
qSqSP 11
Г
,
щоб знайти q, візьмемо випадкову величину
,1
Г
−
σ
=χ n
S
(430)
що має розподіл
χ
(хі-розподіл).
Ураховуючи те, що події
()
(
)
(
)
qSqSA
+
<
σ<− 11
Г
і
() ()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
<
σ
<
+
qSqS
B
1
11
1
1
Г
при q < 1 є рівноймовірними, маємо:
() ()()
()
()
.
1
11
1
1
11
Г
Г
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
<
σ
<
+
=+<σ<−
qSqS
PqSqSP
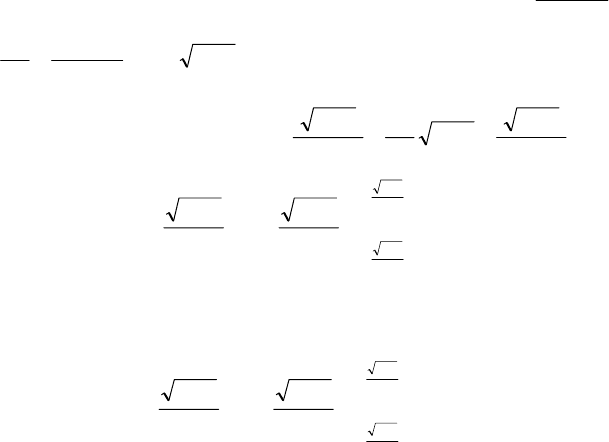
69
Якщо помножити всі члени подвійної нерівності
()
<
+ qS 1
1
()
qS −
<
σ
<
1
11
Г
на
,1−nS
то дістанемо:
() ()()
() ()
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
<−
σ
<
+
−
=+<σ<−
qS
n
n
S
qS
n
PqSqSP
1
1
1
1
1
11
Г
Г
()
γ==
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
<χ<
+
−
=
∫
−
−
+
−
q
n
q
n
dttf
q
n
q
n
P
1
1
1
1
1
1
1
1
.
Звідси маємо:
(
)
(
)
(
)
()
.γ
1
1
χ
1
1
11
1
1
1
1
Г
==
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
<<
+
−
=
=
+
<
<
−
∫
−
−
+
−
q
n
q
n
dttf
q
n
q
n
P
qSσqSP
(431)
З рівняння (431) за заданою надійністю
γ
і обсягом вибір-
ки n знаходимо за таблицею (додаток 5) значення величини
q(
γ
; n).
Довірчий інтервал буде таким:
(
)()
(
)
(
)
nqSnqS ;1;1
Г
γ
+
<
σ
<
γ−
. (432)
Приклад. З надійністю 99,0
=
γ
побудувати довірчий ін-
тервал для
Г
σ
. Якщо S = 45, n = 30.
Розв’язання. Для побудови довірчого інтервалу обчислимо значен-
ня
()
nq ;γ за таблицею (додаток 5). ( 99,0
=
γ
; n = 30) = 0,43.
Визначимо кінці інтервалу:
()()
(
)
;565,257,05,443,015,4;1
=
⋅
=
−
=
γ− nqS
()()
(
)
.435,643,15,443,015,4;1
=
⋅
=
+
=
γ
+ nqS
Отже, довірчий інтервал для
Г
σ
з надійністю
99,0
=
γ
буде таким:
.435,6565,2
Г
<
σ
<
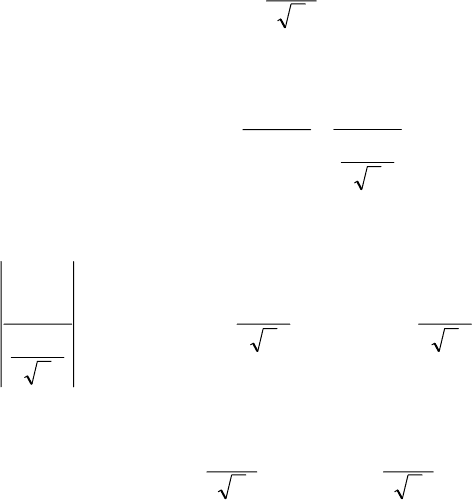
70
9. Побудова довірчого інтервалу
для r
xy
генеральної сукупності
із заданою надійністю
γ
Як величина, одержана за результатами вибірки,
B
r є випад-
ковою і являє собою точкову незміщену статистичну оцінку для
xy
r
()
(
)
.
B xy
rrM =
Виправлене середнє квадратичне відхилення для
B
r
.
1
2
B
n
r
S
−
= (433)
Для побудови довірчого інтервалу для
xy
r
використовується
випадкова величина
()
,
1
2
B
B
B
n
r
rr
r
rr
x
xyxyB
−
−
=
σ
−
=
γ
(434)
що має нормований нормальний закон розподілу N(0; 1).
Скориставшись (434), дістанемо
()
.2
11
1
2
B
B
2
B
B
2
B
B
γγγγ
=γ=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−<<
−
−=
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
<
−
−
xФ
n
r
trr
n
r
trPx
n
r
rr
P
xy
xy
Отже, довірчий інтервал для
xy
r буде таким:
,
11
2
B
B
2
B
B
n
r
trr
n
r
tr
xy
−
+<<
−
−
γγ
(435)
де t
γ
знаходимо з рівності
(
)
γ
=
γ
5,0xФ
за таблицею значень функції Лапласа.
Приклад. Випадково вибраних студентів із потоку універ-
ситету було піддано тестуванню з математики і хімії. Ре-
зультати цих тестувань подано двовимірним статистичним
розподілом, де
i
xX
=
— оцінки з математики,
i
yY =
— із
хімії. Відповіді оцінювалися за десятибальною системою:
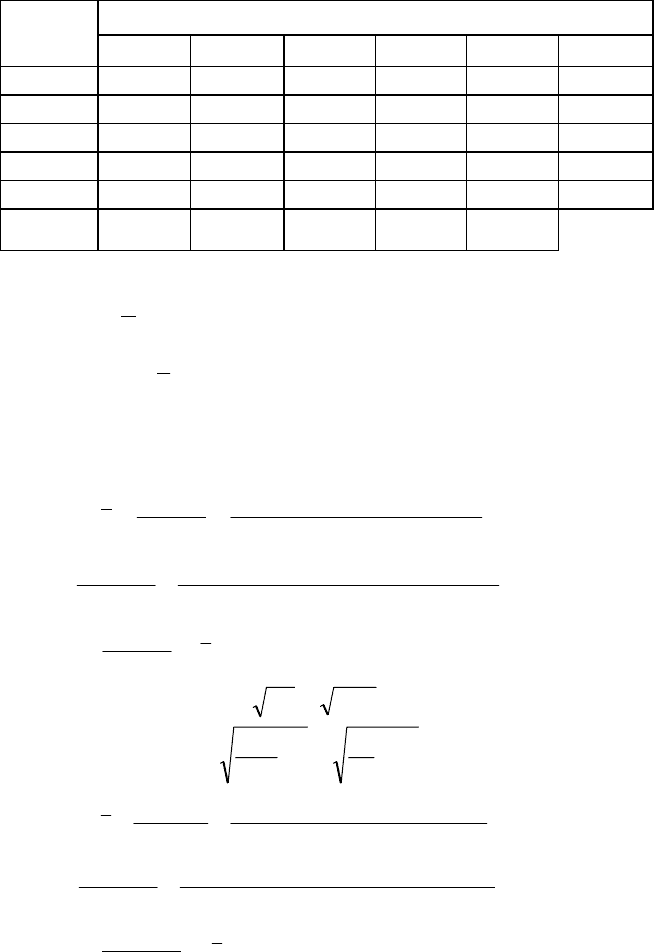
71
Y = y
i
Х = х
і
1 3 5 7 9
i
y
n
1 2 2 1 — — 5
3 1 1 1 1 — 4
5 — — 1 2 3 6
7 — — 1 1 4 6
9 — — 2 3 4 9
j
x
n
3 3 6 7 11
Необхідно:
1) з надійністю
99,0
=
γ
побудувати довірчий інтервал для
Г
X
, якщо
;5
Г
=
σ
2) з надійністю
999,0
=
γ
побудувати довірчі інтервали для
,
Г
σ
,
Г
Y
xy
r
.
Розв’язання. Обчислимо основні числові характеристики ознак Х і
Y, а також
,
*
xy
K
B
r
. Оскільки
∑∑
=
=
,30
ij
nn
дістанемо:
;33,6
30
11977653331
=
⋅+⋅+⋅+⋅+⋅
==
∑
n
nx
x
j
xi
.13,47
30
11977653331
22222
2
=
⋅+⋅+⋅+⋅+⋅
=
∑
n
nx
j
xi
() ( )
;06,707,4013,4733,613,47
22
=−=−=−=
∑
x
n
nx
D
j
xi
x
.66,206,7 ≈==σ
xx
D
.7,206,7
29
30
1
≈=
−
=
xx
D
n
n
S
.67,5
30
9967654351
=
⋅+⋅+⋅+⋅+⋅
==
∑
n
ny
y
i
yi
.47,40
30
9967654351
22222
2
=
⋅+⋅+⋅+⋅+⋅
=
∑
n
ny
ii
y
() ( )
.32,815,3247,4067,547,40
22
2
=−=−=−=
∑
y
n
ny
D
ii
y
y
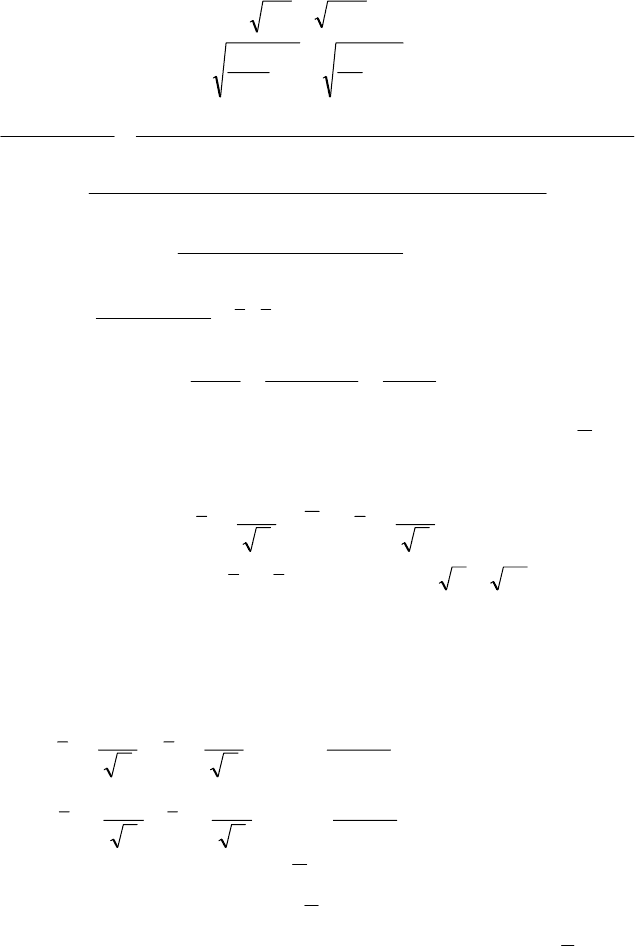
72
.88,232,8 ≈==σ
yy
D
.93,232,8
29
30
1
≈=
−
=
yy
D
n
n
S
30
713513313113511321121 +⋅⋅+⋅⋅+⋅⋅+⋅⋅+⋅⋅+⋅⋅+⋅⋅
=
∑∑
n
nxy
i
yii
30
947717517935725515
+
⋅
⋅
+
⋅
⋅
+
⋅
⋅
+
⋅
⋅
+
⋅
⋅+⋅⋅+
.41
30
949739529
=
⋅
⋅
+
⋅
⋅
+
⋅
⋅
+
.11,589,354167,533,641
*
=−=⋅−=⋅−=
∑∑
yx
n
nxy
K
iyii
xy
.667,0
661,7
11,5
88,266,2
11,5
*
B
≈=
⋅
=
σσ
=
yx
xy
K
r
1. Побудуємо довірчий інтервал з надійністю
99,0
=
γ
для
Г
X
, як-
що
Г
σ
= 5.
.
Г
BГ
Г
B
n
x
xX
n
x
x
σ
+<<
σ
−
Нам відомі значення
,33,6
B
=
=
xx 5
Г
=
σ
,
.48,530 ==n
Зна-
чення х обчислюємо з рівняння
()
,495,099,05,05,0
=
⋅
=
γ
=
xФ
де х = 2,58 знаходимо за таблицею значень функції Лапласа.
Визначимо кінці інтервалу:
;98,335,233,6
48,5
558,2
33,6
Г
B
Г
B
=−=
⋅
−=
σ
−=
σ
−
n
x
x
n
x
x
.68,835,233,6
48,5
558,2
33,6
Г
B
Г
B
=+=
⋅
+=
σ
+=
σ
+
n
x
x
n
x
x
Отже, довірчий інтервал для
Г
X
буде таким:
.68,898,3
Г
<< Х
2. Побудуємо довірчий інтервал з надійністю γ = 0,999 для
.
Г
Y
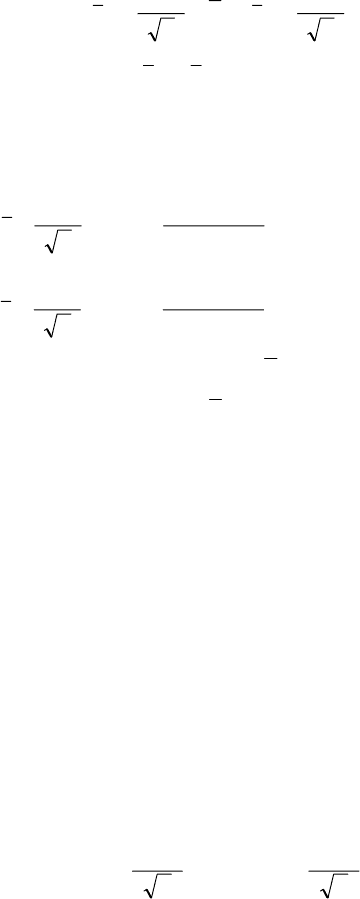
73
Оскільки
Г
σ
нам не відоме, то довірчий інтервал у цьому разі ви-
значається так:
.
BГB
n
St
yY
n
St
y
yy γγ
+<<−
Нам відоме значення ,67,5
B
=
=
yy
,93,2
=
y
S
γ
t
знаходимо за
таблицею розподілу Стьюдента (додаток 3).
(
)
.659,329,999,0
=
=
=
γ kt
Обчислимо кінці довірчого інтервалу:
;72,395,167,5
5,5
93,2659,3
67,5 =−=
⋅
−=−
γ
n
St
y
y
.62,795,167,5
5,5
93,2659,3
67,5 =+=
⋅
+=+
γ
n
St
y
y
Таким чином, довірчий інтервал для
Г
Y буде в таких межах:
.62,772,3
Г
<< Y
Довірчий інтервал з надійністю γ = 0,999 для
Г
σ
буде таким:
(
)()
(
)
(
)
.;1;1
Г
nqSnqS
yy
γ
−
<
σ
<
γ
−
Нам відоме значення
93,2
=
y
S
. Враховуючи, що γ = 0,999, n = 30,
знайдемо за таблицею (додаток 5) значення
(
)
63,030,999,0
=
=
=
γ
nq
.
Визначимо кінці довірчого інтервалу:
()()
(
)
;084,137,093,263,0193,2;1
=
⋅
=
−
=
γ
− nqS
y
()()
(
)
.776,463,193,263,0193,2;1
=
⋅
=
+
=
γ+ nqS
y
Отже, довірчий інтервал для
Г
σ
подається такою нерівністю:
.776,4084,1
Г
<
σ
<
Довірчий інтервал для
xy
r із заданою надійністю γ = 0,999 буде таким:
.
11
2
B
B
2
B
B
n
r
trr
n
r
tr
xy
−
+<<
−
−
γγ
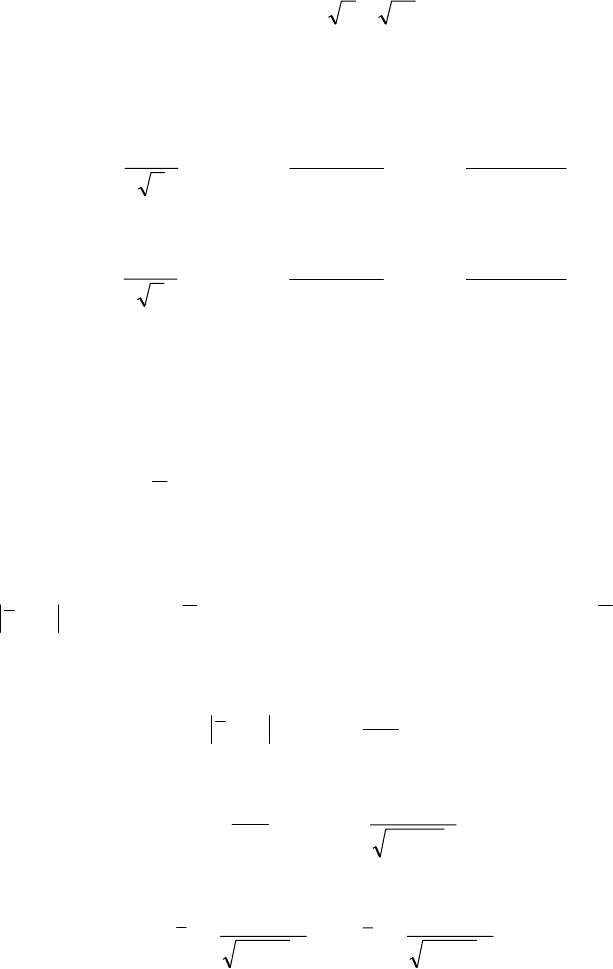
74
Нам відомі значення ,67,0
B
=
r
,48,530 ≈=n
γ
t
визначаємо за
таблицею значень функції Лапласа
(
)
=
⋅
=
γ
=
γ
999,05,05,0xФ
,4995,0
де
.2,3=
γ
x
Визначимо кінці довірчого інтервалу:
(
)
;348,0322,067,0
48,5
5511,02,3
67,0
48,5
67,01
2,367,0
1
2
2
B
B
=−=
=
⋅
−=
−
−=
−
−
γ
n
r
xr
(
)
.992,0322,067,0
48,5
5511,02,3
67,0
48,5
67,01
2,367,0
1
2
2
B
B
=+=
=
⋅
+=
−
+=
−
+
γ
n
r
xr
Таким чином, довірчий інтервал для
xy
r буде в таких межах:
.992,0348,0
<
<
xy
r
10. Побудова довірчого інтервалу
для
Г
X за допомогою нерівності Чебишова
із заданою надійністю
γ
У разі, коли відсутня інформація про закон розподілу ознаки
генеральної сукупності Х, оцінювання ймовірності події
δ<− ax
B
, де
,
Г
Xa
= та побудова довірчого інтервалу для
Г
X
із
заданою надійністю
γ
виконуються з використанням нерівності
Чебишова за умови, що відоме значення
Г
σ
, а саме:
()
γ=
δ
σ
−≥δ<−
2
2
Г
B
1
n
axP . (436)
Із (436) визначаємо величину δ:
()
.
1
1
2
Г
2
2
Г
n
n
γ−
σ
=δ→γ=
δ
σ
−
(437)
Довірчий інтервал подається такою нерівністю:
() ()
n
xa
n
x
γ−
σ
+<<
γ−
σ
−
11
Г
B
Г
B
. (438)
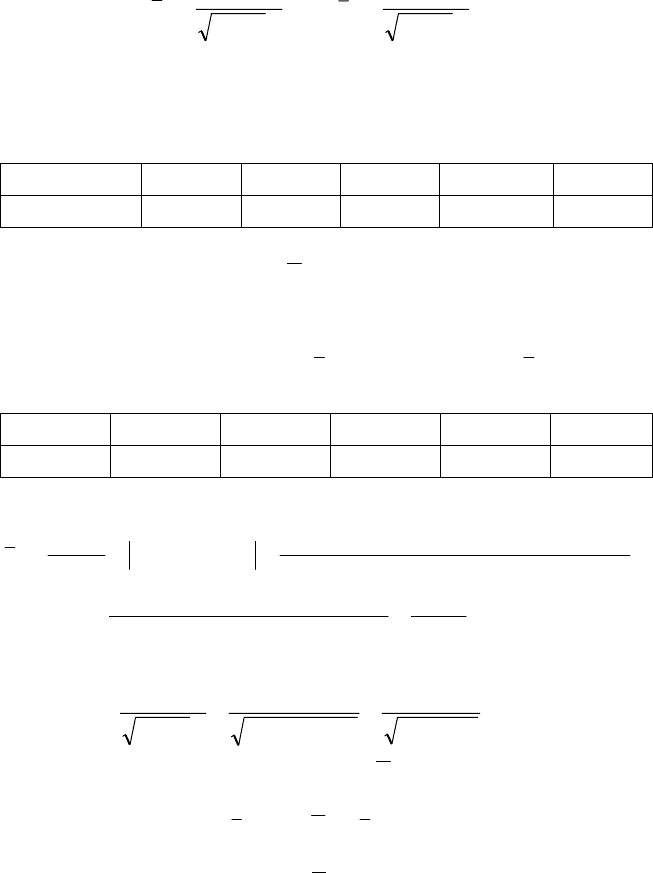
75
Коли
Г
σ невідоме, застосовуємо виправлену дисперсію
2
S
, і
довірчий інтервал набирає такого вигляду:
() ()
n
S
xa
n
S
x
γ−
+<<
γ−
−
11
BB
. (439)
Приклад. Одержано дані зі 100 навмання вибраних підп-
риємств щодо зростання виробітку на одного робітника х
і
(у % відносно попереднього року), які мають такий інтер-
вальний статистичний розподіл:
х
і
, %; h = 10 80—90 90—100 100—110 110—120 120—130
n
i
3 14 60 20 4
Використовуючи нерівність Чебишова, побудувати довір-
чий інтервал для
,
Г
X
якщо відоме значення %5
Г
=
σ
з
надійністю γ = 0,99.
Розв’язання. Для побудови довірчого інтервалу з допомогою нерівнос-
ті Чебишова необхідно обчислити
,
B
x
δ. Щоб визначити
B
x
, перейдемо
від інтервального до дискретного статистичного розподілу, а саме:
x
i
85 95 105 115 125
n
i
3 14 60 20 4
Тоді маємо:
=
⋅+⋅+⋅+⋅+⋅
=====
∑
∑
101
412520115601051495385
101
B i
ii
nn
n
nx
x
%8,105
101
10685
101
500230063001330255
==
++++
=
.
Використовуючи (437), обчислимо δ:
() ()
%.98,4
10101,0
5
10199,01
5
1
Г
=
⋅
=
−
=
γ−
σ
=δ
n
Таким чином, довірчий інтервал для
Г
X
подається такими нерівно-
стями:
δ+<<δ−
BГB
xXx
,
або
.8,1108,100
Г
<<
X
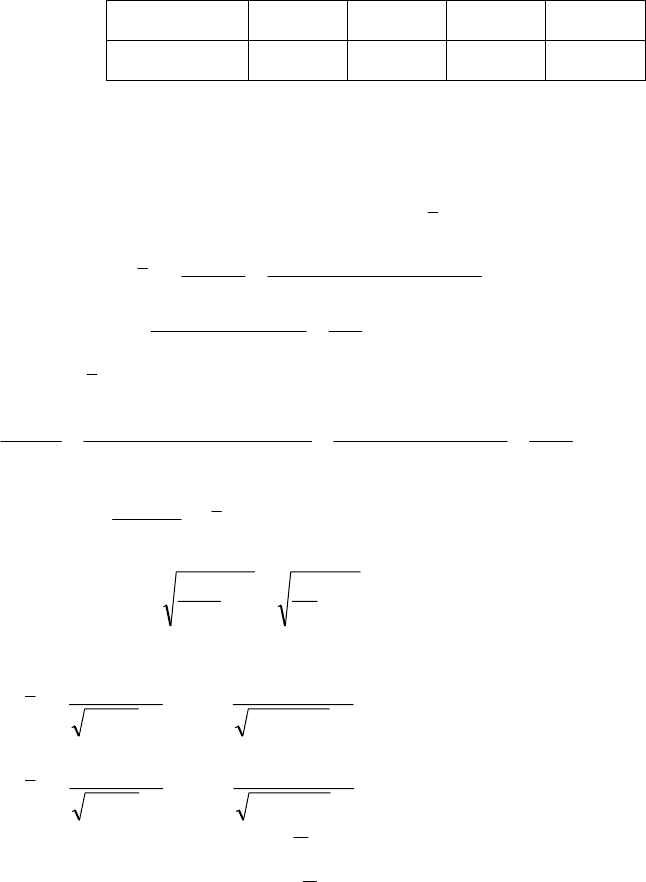
76
Приклад. Задані розміри основних фондів х
і
на 30-ти під-
приємствах дискретним статистичним розподілом:
x
i
, млн грн. 3 5 7 9
n
i
9 7 10 4
Використовуючи нерівність Чебишова з надійністю γ = 0,99,
побудувати довірчий інтервал для
Г
X
.
Розв’язання. Для побудови довірчого інтервалу для
Г
X
за допомо-
гою нерівності Чебишова необхідно обчислити
B
x
,
S
:
грн.млн6,5
30
168
30
36703527
30
491077593
B
==
+++
=
=
⋅+⋅+⋅+⋅
==
∑
n
nx
x
ii
Отже,
.грнмлн6,5
B
=
x
.7,35
30
1070
30
32449017581
30
481104972599
2
==
+++
=
⋅+⋅+⋅+⋅
=
∑
n
nx
ii
() ()
.34,436,317,356,57,35
22
B
2
В
=−=−=−=
∑
x
n
nx
D
ii
.грнмлн12,234,4
29
30
1
B
≈=
−
= D
n
n
S
Визначимо кінці довірчого інтервалу:
() ()
грн.;млн73,187,36,5
3099,01
12,2
6,5
301
B
=−=
−
−=
γ−
−
S
x
() ()
.грнмлн47,987,36,5
3099,01
12,2
6,5
301
B
=+=
−
+=
γ−
+
S
x
Отож, довірчий інтервал для
Г
X
подається нерівностями
.47,973,1
Г
<< X
