Жлуктенко В. І., Наконечний С. І., Савіна С.С. Теорія ймовірностей і математична статистика: У 2-х ч. - Ч. ІІ. Математична статистика
Подождите немного. Документ загружается.

96
Критичні точки у цьому разі визначаються за таблицею (дода-
ток 6) заданим рівнем значущості
α
та числом ступенів свободи
k = n – 1. Спостережуване значення критерію обчислюється за
формулою
n
S
ax
t
−
=
∗
B
.
Приклад. Розбіжність вимірів діаметрів кульок X = x
i
є
випадковою величиною, що має закон розподілу N(a; 4).
При рівні значущості α = 0,01 перевірити правильність
240:
0
=aH
мм, якщо альтернативна гіпотеза
240:
>
α
aH мм,
коли відомо, що
Г
σ
= 4 мм і вибіркове середнє значення
виміряних у 100 однотипних кульок
B
x
= 225 мм.
Розв’язання. Оскільки
240:
>
α
aH мм, будується правобічна кри-
тична область. Для цього необхідно знайти критичну точку і побудува-
ти правобічну критичну область. Для знаходження критичної точки за-
стосовуємо відомий вираз:
49,0
2
98,0
2
02,01
2
01,021
2
21
)(Ф
рк
==
−
=
⋅−
=
α−
=z .
За значенням
49,0)(Ф
рк
=
z і скориставшись таблицею (додаток 2)
знаходимо
34,2
рк
≈z . Отже, правобічна критична область матиме ви-
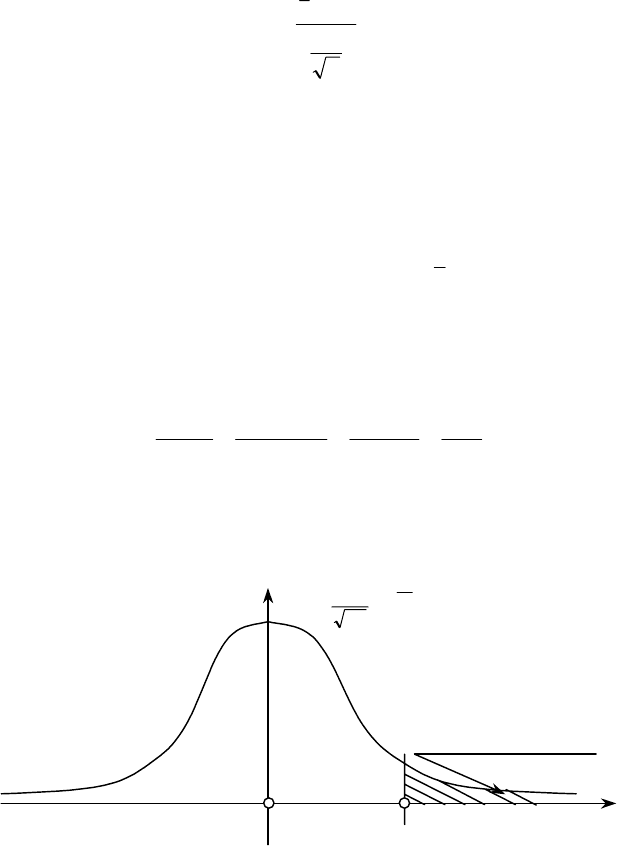
гляд, зображений на рис. 126.
()
2
2
2
1
z
ezf
−
⋅
π
=
0
Критична область
z
z
кр
= 2,34
Рис. 126
97
Обчислимо спостережуване значення критерію за формулою (451)
n
ax
z
Г
B
σ
−
=
∗
. Оскільки
B
x
= 225 мм, а = 240 мм,
4
=
σ
r
мм, n = 100, маємо
.5,37
4
150
4,0
15
10
4
15
100
4
240225
−=−=−=
−
=
−
=
∗
z
Висновок. Оскільки
]34,2;]
*
∞−∈z
, то немає підстав
для відхилення нульової гіпотези
=
aH :
0
240 мм.
Отже, нульова гіпотеза приймається.
Приклад. Проведено 10 незалежних експериментів над
випадковою величиною Х, що має нормальний закон роз-
поділу з невідомими значеннями а, σ. Наслідки експери-
ментів подано у вигляді статистичного ряду:
x
i
2,5 2 –2,3 1,9 –2,1 2,4 2,3 –2,5 1,5 –1,7
n
i
1 1 1 1 1 1 1 1 1 1
При рівні значущості α = 0,001 перевірити правильність
нульової гіпотези
9,0:
0
=aH , при альтернативній гіпотезі
9,0: <
α
aH
.
Розв’язання. Запишемо статистичний ряд у вигляді статистичного
розподілу й обчислимо
Sx ,
B
:
x
i
–2,5 –2,3 –2,1 –1,7 1,5 1,9 2 2,3 2,4 2,5
n
i
1 1 1 1 1 1 1 1 1 1
.4,0
10
5,24,23,229,15,17,11,23,25,2
=
+
+
+
+
+
+
−
−
−−
=
∑
=
n
x
x
i
B
=−
∑
=
2
2
)(
BB
x
n
x
D
i
=−
+
+
+
+
+
+
+++
=
2
)4,0(
10
25,676,529,5461,325,289,241,429,525,6
44,416,06,4
=
−
=
.

98
933,444,4
9
10
1
2
=⋅=
−
=
B
D
n
n
S
.
22,2933,4 ≈=S
.
При альтернативній гіпотезі
9,0:
<
α
aH
будується лівобічна
критична область. Для цього необхідно знайти критичну точку,
застосовуючи статистичний критерій (451). За таблицею (дода-
ток 6) знаходимо значення
)91101,001,0(
рк
=
−
=
−
==
α
nkt
=
78,4)9,001,0(
=
=
=
α
kt
.
Оскільки щільність ймовірностей для розподілу Стьюдента є
парною, то
78,4
кр
−=t
.
Критична область показана на рис. 127.
Критична область
()
2
1
2
1
2
Г
2
1
Г
1
+
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
π
=
k
k
t
k
k
k
tf
0
t
t
кр
= –4,78
Рис. 127
Обчислимо спостережуване значення критерію:
712,0
702,0
5,0
702,0
9,04,0
16,3
22,2
9,04,0
10
22,2
9,04,0
−=−=
−
=
−
=
−
=
−
=
∗
n
S
ax
t
B
.
Висновок. Оскільки
[
[
∞−∈
∗
;78,4t
, то немає підстав
відхилити
9,0:
0
=
aH
.
Приклад. Реалізувавши вибірку з генеральної сукуп-
ності, ознака якої Х має нормальний закон розподілу,
дістали статистичний розподіл:
99
x
i
6 7 8 9 10 11 12 13 14
n
i
1 3 6 8 6 6 5 3 2
При рівні значущості α = 0,01 перевірити правильність ну-
льової гіпотези
8:
0
=aH , якщо альтернативна гіпотеза 8:
≠
α
aH .
Розв’язання. Обчислимо значення Sx ,
B
:
=====
∑
∑
40 якТак
B i
ii
nn
n
nx
x
=
⋅
+
⋅
+
⋅
+
⋅
+
⋅
+
⋅
+⋅+⋅+
=
40
2143135126116108968376
10
40
28396066607248216
=
++++++++
= .
=−=
∑
2
2
)(
BB
x
n
nx
D
ii
=−
⋅+⋅+⋅+⋅+⋅+⋅+⋅+⋅+
=
2
)10(
40
2196316951446121610088166434936
=−
+
+
+
+
+
+++
= 100
40
39250772072660064838414736
4100104100
40
4160
=−=−=
.
103,44
39
40
1
B
2
=⋅=
−
= D
n
n
S
.
03,2103,4 ≈=S
.
При альтернативній гіпотезі
8:
≠
α
aH
будуємо двобічну критичну
область. Враховуючи, що σ
Г
є невідомою величиною, для побудови цієї
області беремо статистичний критерій (452).
Оскільки критичні точки
рк
t
′
і
рк
t
′
′
симетричні відносно нуля і при
цьому
рк
t
′
= –
рк
t
′′
, знаходимо за таблицею (додаток 6)
рк
t
′
′
:
7,2)39;01,0()391401,01,0(
ркрк
=
=
=
α
′
′
=
=
−
=
−==
α
′′
ktnkt
.
Тоді
рк
t
′
= – 2,7.
Двобічна критична область зображена на рис. 128.
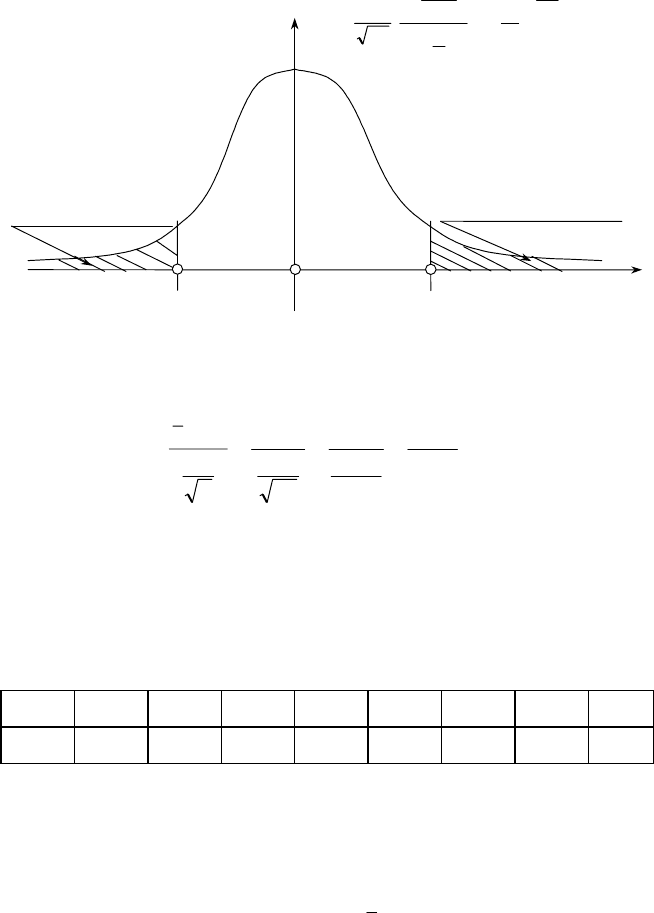
100
()
2
1
2
1
2
Г
2
1
Г
1
+
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
+
π
=
k
k
t
k
k
k
tf
0
Критична область
z
Критична область
t′
кр
= – 2,7 t
″
кр
= – 2,7
Рис. 128
Обчислимо спостережуване значення критерію:
23,6
321,0
2
325,6
03,2
2
40
03,2
810
===
−
=
−
=
∗
n
S
ax
t
B
.
Висновок. Оскільки
[
]
708,2;708,2−∈
∗
t , то немає під-
став приймати
8:
0
=
aH .
Приклад. З генеральної сукупності, ознака якої Х має за-
кон розподілу N(a; 5), реалізована вибірка і побудовано
статистичний розподіл:
x
i
10,9 11 11,2 11,3 11,5 11,6 11,8 11,9
n
i
2 4 1 3 4 1 2 3
При рівні значущості α = 0,01 перевірити правильність ну-
льової гіпотези
44,11:
0
=aH
при альтернативній гіпотезі
44,11: ≠
α
aH
.
Розв’язання. Обчислимо значення
B
x
. Оскільки
∑
=
=
20
i
nn
, то
дістанемо
101
=
⋅+⋅+⋅+⋅+⋅+⋅+⋅+⋅
=
==
∑
20
39,1128,1116,1145,1133,1112,1141129,10
n
nx
x
ii
B
39,11
20
8,227
20
7,356,236,11469,332,11448,21
==
+++++++
=
.
При альтернативній гіпотезі
44,11:
≠
α
aH
будується двобічна кри-
тична область. Враховуючи те, що відоме значення
Г
σ
= 5, для знахо-
дження критичних точок скористаємося статистичним критерієм
n
ax
z
Г
B
σ
−
=
, що має закон розподілу N(0; 1).
Критична точка
рк
z
′′
визначається з рівності
495,0
2
99,0
2
01,01
2
1
)(Ф
рк
==
−
=
α
−
=
′′
z
.
За значенням функції Лапласа
495,0)(Ф
р
=
′
′
к
z
знаходимо
рк
z
′′
= 2,58.
Оскільки
рк
z
′
= –
рк
z
′′
, то маємо
рк
z
′
= – 2,58.
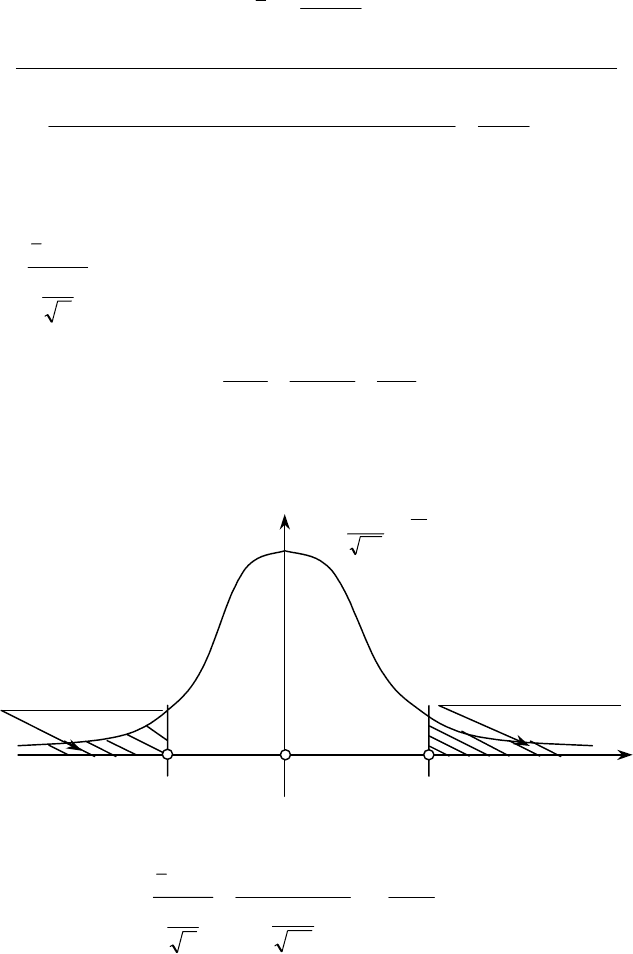
Двобічна критична область зображена на рис. 129.
()
2
2
2
1
z
ezf
−
⋅
π
=
0
Критична область
z
z
′
кр
= – 2,58
Критична область
z
″
кр
= 2,58
Рис. 129
Обчислимо спостережуване значення критерію
045,0
119,1
05,0
20
5
44,1139,11
Г
−≈−=
−
=
σ
−
=
∗
n
ax
z
B
.
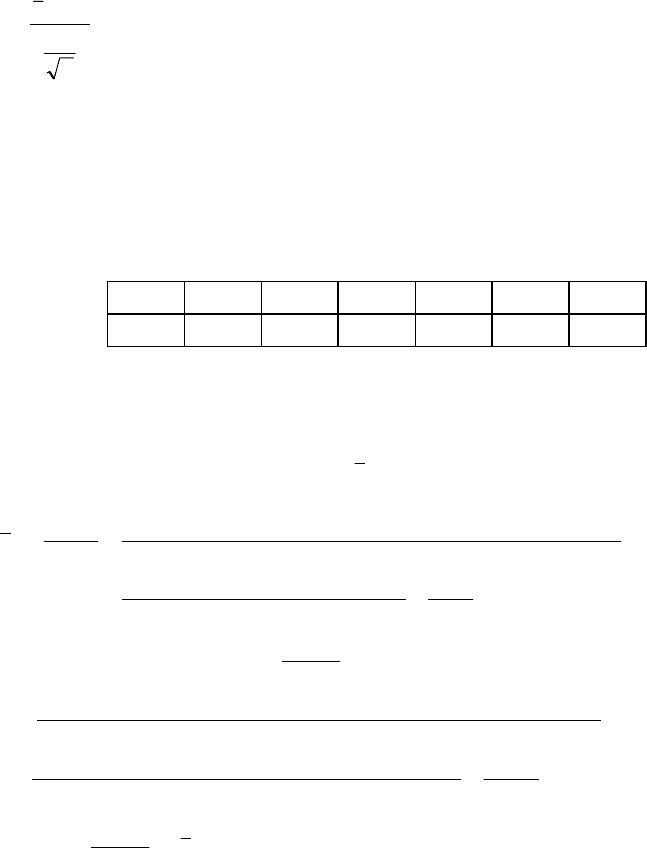
102
Висновок. Оскільки
[
]
58,2;58,2−∈
∗
z
, немає підстав
відхиляти
44,11:
0
=
aH .
При великих обсягах вибірки (n > 40) статистичний критерій
n
S
ax
z
−
=
B
, що має закон розподілу Стьюдента з k = n – 1 ступе-
нями свободи, наближається асимптотично до нормованого нор-
мального закону N(0; 1). У цьому разі критичні точки визнача-
ються з рівностей (448) — (450).
Приклад. Реалізувавши вибірку з генеральної сукупності,
елементами якої є однотипні заготівки, довжина яких Х є
випадковою величиною з нормальним законом розподілу,
дістали статистичний розподіл:
x
i
6,5 8,5 10,5 12,5 14,5 16,5
n
i
10 20 30 20 10 10
Якщо рівень значущості α = 0,001, перевірити правильність
5,15:
0
=aH
при альтернативній гіпотезі
5,15:
>
α
aH .
Розв’язання. Обчислимо значення
Sx ,
B
. Оскільки
∑
=
=
100
i
nn
,
то маємо
=
⋅
+
⋅
+
⋅
+
⋅
+
⋅
+⋅
=
∑
=
100
105,16105,14205,12305,10205,8105,6
n
nx
x
ii
B
1,11
100
1110
100
16514525031517065
==
+++++
=
;
=
⋅+⋅+⋅+⋅+⋅+⋅
=
=
∑
100
1025,2721025,2102025,1563025,1102025,721025,42
2
n
nx
ii
25,131
100
13125
100
5,27225,210231255,33075,1445,422
==
+
+
+
++
=
.
04,821,12325,131)1,11(25,131)(
22
2
=−=−=−
∑
=
BB
x
n
nx
D
ii
.
103
12,804,8
99
100
1
2
=⋅=
−
=
B
D
n
n
S
.
85,212,8
≈=S
.
Оскільки обсяг вибірки великий (n = 100 > 40), статистичний
критерій
n
S
ax
t
−
=
B
наближатиметься до закону розподілу N(0; 1).
Тому для визначення критичної точки
кркр
zt
=
застосовуємо рів-
ність
2,3499,0
2
998,0
2
001,021
2
21
)(Ф
ркрк
=→==
⋅−
=
α−
= zz
.
Правобічна критична область матиме такий вигляд (рис. 130):
0
()
2
2
2
1
z
ezf
−
⋅
π
=
Критична область
z
z
кр
= 3,2
Рис. 130
Обчислимо спостережуване значення критерію
44,15
285,0
4,4
100
85,2
5,151,11
−≈−=
−
=
−
=
∗
n
S
ax
z
B
.
104
Висновок. Оскільки
]44,5;]
*
∞−∈z
, то
5,15:
0
=aH
приймається.
9.2. Перевірка правильності
нульової гіпотези про рівність
двох генеральних середніх (M(X) = M(Y))
Нехай задано дві генеральні сукупності, ознаки яких Х і Y ма-
ють нормальний закон розподілу і при цьому незалежні одна від
одної. Необхідно перевірити правдивість
)()(:
0
YMXMH =
)(
ГГ
YX =
.
Тут можуть спостерігатися два випадки:
Випадок 1. Обсяг вибірки великий (n > 40) і відомі значен-
ня
Гx
DD ,
ознак генеральних сукупностей.
З кожної генеральної сукупності здійснюють вибірку відпові-
дно з обсягами
n
′
і
n
′
′
і будують статистичні розподіли:
x
i
x
1
x
2
x
3
.....
.
x
k
y
j
y
1
y
2
y
3
...... y
m
i
n
′
1
n
′
2
n
′
3
n
′
.....
.
k
n
′
j
n
′
′
1
n
′′
2
n
′′
3
n
′′
......
m
n
′′
Тут
∑∑
′
′
=
′′′
=
′
ji
nnnn
,
.
Обчислюються значення
n
ny
y
n
nx
x
jj
ii
′′
′
′
=
′
′
=
∑
∑
BB
, .
За статистичний критерій береться випадкова величина
)(
BB
BB
yx
yx
Z
−σ
−
=
, (453)
що має закон розподілу N(0; 1).
Оскільки
n
D
n
D
yxD
y
x
′′
+
′
=− )(
BB
, то статистичний критерій
(453) набере такого вигляду:
n
D
n
D
yx
Z
y
x
′′
+
′
−
=
BB
. (454)
Коли
DDD
yx
==
, дістанемо:
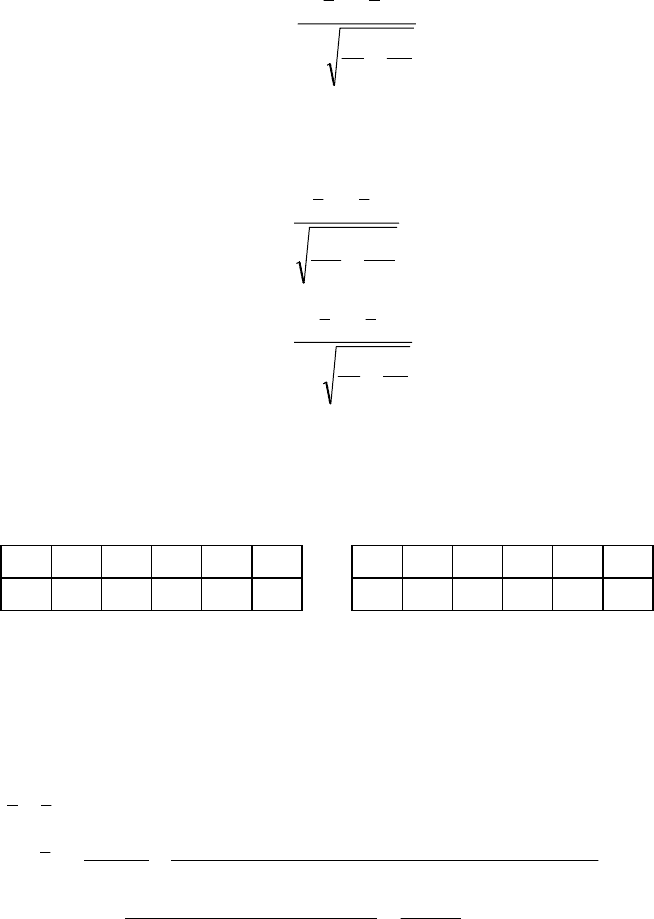
105
21
11
nn
yx
Z
+σ
−
=
Г
BB
. (455)
Залежно від формулювання альтернативної гіпотези Н
α
бу-
дуються відповідно правобічна, лівобічна та двобічна критичні
області.
Спостережуване значення критерію відповідно обчислюється:
n
D
n
D
yx
Z
y
x
′′
+
′
−
=
∗
BB
(456)
або
21
11
nn
yx
Z
+σ
−
=
∗
Г
BB
. (457)
Приклад. За заданими статистичними розподілами двох
вибірок, реалізованих із двох генеральних сукупностей,
ознаки яких мають нормальний закон розподілу зі значен-
ням дисперсій генеральних сукупностей
15;10 =
=
yx
DD
,
x
i
12,2 13,2 14,2 15,2 16,2 y
j
8,4 12,4 16,4 20,4 24,4
i
n
′
5 15 40 30 10
j
n
′
′
10 15 35 20 20
при рівні значущості α = 0,01 перевірити правдивість ну-
льової гіпотези
)()(:
0
YMXMH
=
, якщо альтернативна гіпотеза
.)()(: YMXMH >
α
Розв’язання. Оскільки
∑∑
=
′
′
=
′
′
=
′
=
′
100;100
ji
nnnn
, обчислимо
BB
yx ,
:
=
⋅+⋅+⋅+⋅+⋅
=
′
′
=
∑
100
102,16302,15402,14152,1355,12
n
nx
x
ii
B
465,14
100
5,1446
100
1624565681985,62
==
+
+
+
+
=
.
