Жлуктенко В. І., Наконечний С. І., Савіна С.С. Теорія ймовірностей і математична статистика: У 2-х ч.

57

5. Інтервальні статистичні оцінки

для параметрів генеральної сукупності

Точкові статистичні оцінки

*

θ

є випадковими величинами, а

тому наближена заміна θ на

*

θ

часто призводить до істотних по-

хибок, особливо коли обсяг вибірки малий. У цьому разі застосо-

вують інтервальні статистичні оцінки.

Статистична оцінка, що визначається двома числами, кінцями

інтервалів, називається інтервальною.

Різниця між статистичною оцінкою

*

θ

та її оцінювальним па-

раметром θ, взята за абсолютним значенням, називається точні-

стю оцінки, а саме:

,δθθ

*

<−

(414)

де δ є точністю оцінки.

Оскільки

*

θ

є випадковою величиною, то і δ буде випадковою,

тому нерівність (414) справджуватиметься з певною ймовірністю.

Імовірність, з якою береться нерівність (414), тобто

(

)

γδθθ

*

=<−P , (415)

називають надійністю.

Рівність (415) можна записати так:

(

)

γδθθδθ

2*

=+<<−P . (416)

Інтервал

[]

δθδ;θ +−

∗∗

, що покриває оцінюваний параметр θ ге-

неральної сукупності з заданою надійністю

γ

, називають довірчим.

6. Побудова довірчого інтервалу

для

Г

X при відомому значенні

Г

σ

із заданою надійністю γ

Нехай ознака Х генеральної сукупності має нормальний закон

розподілу. Побудуємо довірчий інтервал для

Г

X

, знаючи числове

значення середнього квадратичного відхилення генеральної су-

купності

,σ

Г

із заданою надійністю γ. Оскільки

B

x як точкова не-

зміщена статистична оцінка для

(

)

хМX =

Г

має нормальний за-

кон розподілу з числовими характеристиками

(

)

,

ГB

aXxM ==

()

n

x

Г

B

σ

=σ

, то, скориставшись (416), дістанемо

58

(

)

γδ

B

=<− axP . (417)

Випадкова величина

ax

−

B

має нормальний закон розподілу з

числовими характеристиками

()

(

)

;0

BB

=

−

=

−

=

−

aaaxMaxM

()()

;

Г

BB

n

D

xDaxD ==−

()

.

σ

Г

B

n

x =

Тому

n

ax

Г

B

σ

−

матиме нормований нормальний закон розподілу

N(0; 1).

Звідси рівність (417) можна записати, назначивши

,

Г

x

n

=

σ

δ

так:

γ

Г

B

=

⎟

⎠

⎞

⎜

⎝

⎛

<

σ

−

x

n

ax

P (418)

або

.

Г

B

Г

B

γ=

⎟

⎠

⎞

⎜

⎝

⎛

σ⋅

+<<

σ⋅

−

n

x

xa

n

x

xP

Згідно з формулою нормованого нормального закону

(

)

(

)

δ=δ<− ФaXP 2

для (418) вона набирає такого вигляду:

()

.2

Г

B

γ==

⎟

⎠

⎞

⎜

⎝

⎛

<

σ

−

xФx

n

ax

P

(419)

З рівності (419) знаходимо аргументи х, а саме:

(

)

(

)

.5,02 γ

=

→γ

=

хФхФ

Аргумент х знаходимо за значенням функції Лапласа, яка до-

рівнює 0,5 γ за таблицею (додаток 2).

59

Отже, довірчий інтервал дорівнюватиме:

n

x

xa

n

x

Г

B

Г

B

σ

⋅

+<<

σ

⋅

− , (420)

що можна зобразити умовно на рис. 118.

аX =

Г

n

x

Г

B

σ

−

n

x

Г

B

σ

+

Рис. 118

Величина

n

x

Г

σ⋅

називається точністю оцінки, або похибкою

вибірки.

Приклад.

Вимірявши 40 випадково відібраних після виго-

товлення деталей, знайшли вибіркову середню, що дорів-

нює 15 см. Із надійністю

99,0

=

γ

побудувати довірчий ін-

тервал для середньої величини всієї партії деталей, якщо

генеральна дисперсія дорівнює

2

cм09,0

.

Розв’язання

. Для побудови довірчого інтервалу необхідно знати:

,

B

x

Г

σ , n, x.

З умови задачі маємо:

,см15

В

=

x

===σ

2

ГГ

см09,0D ,cм3,0

.32,64040 ==→= nn Величина х обчислюється з рівняння

()

.495,099,05,05,0

=

⋅

=

γ

=

хФ

()

[

]

.Лапласафункціїзначеньтаблицеюза58,2495,0 =→= ххФ

Знайдемо числові значення кінців довірчого інтервалу:

.см88,1412,015

32,6

58,23,0

15

Г

B

=−=

⋅

−=

⋅σ

−

n

x

.см12,1512,015

32,6

58,23,0

15

B

=+=

⋅

+=

⋅σ

+

n

х

x

Г

Таким чином, маємо:

12,1588,14

Г

<< X .

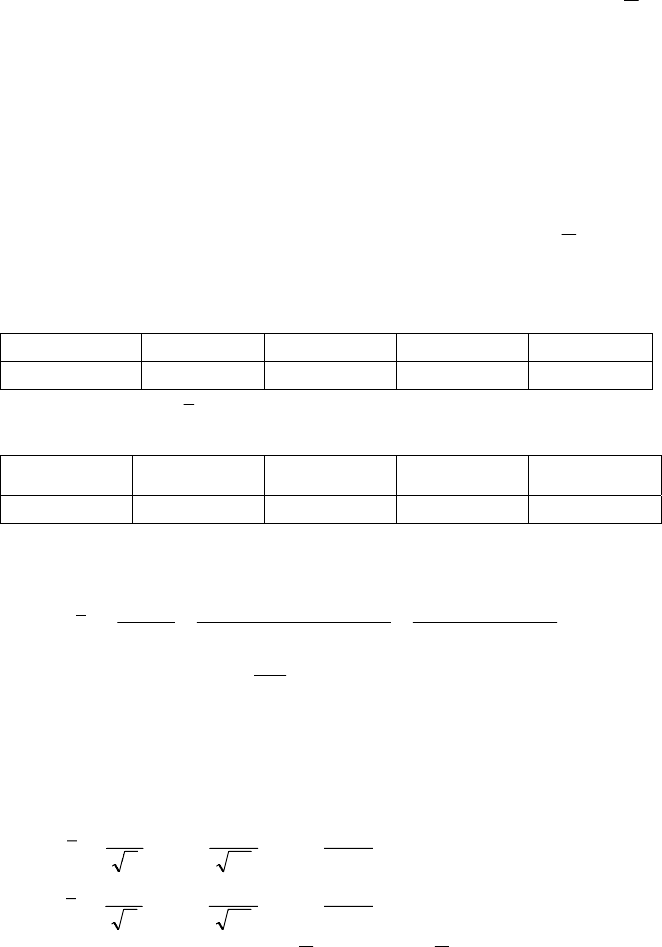
60

Отже, з надійністю 0,99 (99% гарантії) оцінюваний параметр

Г

X

перебуває усередині інтервалу [14,87; 15,13].

Приклад.

Маємо такі дані про розміри основних фондів

(у млн грн.) на 30-ти випадково вибраних підприємствах:

4,2; 2,4; 4,9; 6,7; 4,5; 2,7; 3,9; 2,1; 5,8; 4,0;

2,8; 7,8; 4,4; 6,6; 2,0; 6,2; 7,0; 8,1; 0,7,; 6,8;

9,4; 7,6; 6,3; 8,8; 6,5; 1,4; 4,6; 2,0; 7,2; 9,1.

Побудувати інтервальний статистичний розподіл із довжиною кроку

h = 2 млн грн.

З надійністю

999,0=

γ

знайти довірчий інтервал для

Г

X , якщо

Г

σ = 5 млн грн.

Розв’язання

. Інтервальний статистичний розподіл буде таким:

h =

2 млн грн. 2—4 4—6 6—8 8—10

n

i

9 7 10 4

Для визначення

B

x необхідно побудувати дискретний статистичний

розподіл, що має такий вигляд:

*

i

x

3 5 7 9

n

i

9 7 10 4

∑

== 30

i

nn .

Тоді

грн.млн6,5

30

168

30

36703527

30

491077593

*

B

==

=

+++

=

⋅+⋅+⋅+⋅

==

∑

n

nx

x

ii

Для побудови довірчого інтервалу із заданою надійністю

999,0=

γ

необхідно знайти х:

()

.4,34995,0999,05,05,0

≈

→

=

⋅

=

γ

= ххФ

Обчислюємо кінці інтервалу:

грн.млн5,21,36,5

5,5

54,3

6,5

30

54,3

6,5

Г

B

=−=

⋅

−=

⋅

−=

σ

−

n

x

грн.млн7,81,36,5

5,5

54,3

6,5

30

54,3

6,5

Г

B

=+=

⋅

+=

⋅

+=

σ

+

n

x

Отже, довірчий інтервал для

Г

X

буде

7,85,2

Г

<<

X

.

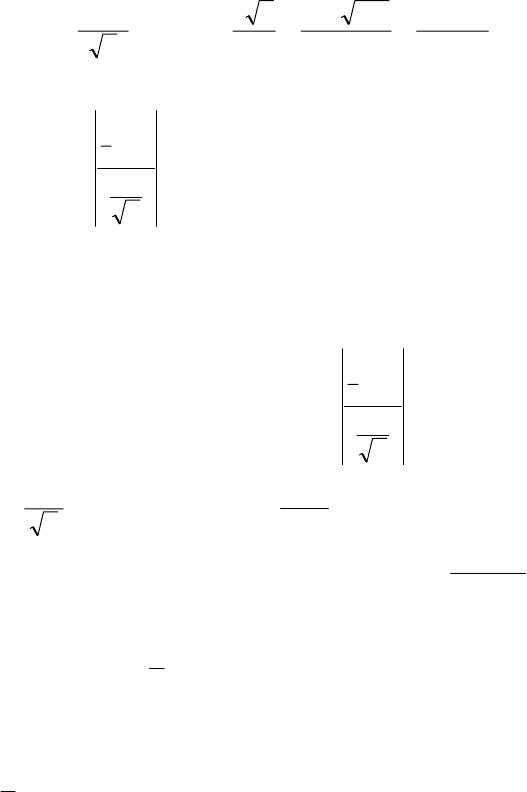
61

Приклад. Якого значення має набувати надійність оцінки

γ, щоб за обсягу вибірки n = 100 похибка її не перевищува-

ла 0,01 при

5

Г

=

σ

.

Розв’язання. Позначимо похибку вибірки

.02,0

5

1001,0

5

10001,0

Г

=

⋅

==

σ

ε

=→ε=

σ⋅ n

х

n

x

Далі маємо:

() ( )

.016,0008,0202,022

Г

B

=⋅===

⎟

⎠

⎞

⎜

⎝

⎛

<

σ

−

ФхФx

n

ax

P

Як бачимо, надійність мала.

Приклад. Визначити обсяг вибірки n, за якого похибка

01,0=ε

гарантується з імовірністю 0,999, якщо

5

Г

=

σ

.

Розв’язання. За умовою задачі

.999,0

Г

B

=γ=

⎟

⎠

⎞

⎜

⎝

⎛

<

σ

−

x

n

ax

P

Оскіль-

ки

,

Г

ε=

σ

n

x

то дістанемо:

.

2

22

Г

ε

σ

=

x

n

Величину х знаходимо з рівності

()

.4,34995,0999,05,05,0

≈

→=⋅=

γ

= ххФ

Тоді

()

.0008902

01,0

54,3

2

=

⋅

=n

7. Побудова довірчого інтервалу

для

Г

X при невідомому значенні

Г

σ

із заданою надійністю

γ

Для малих вибірок, з якими стикаємося, досліджуючи різні

ознаки в техніці чи сільському господарстві, для оцінювання

aX =

Г

при невідомому значенні

Г

σ

неможливо скористатися

нормальним законом розподілу. Тому для побудови довірчого ін-

тервалу застосовується випадкова величина

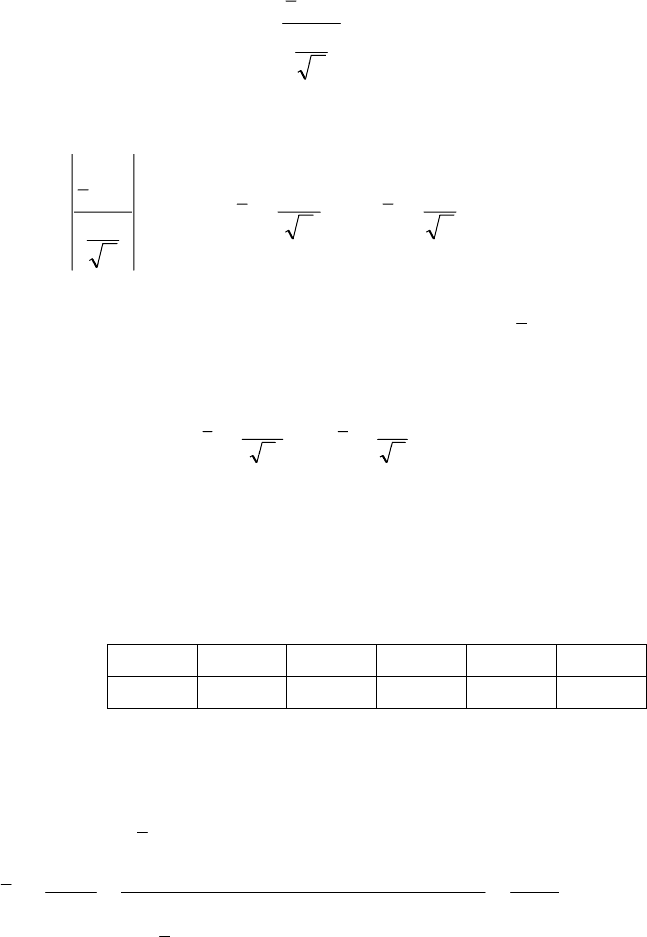
62

,

B

n

S

ax

t

−

= (421)

що має розподіл Стьюдента з

1

−

=

nk

ступенями свободи.

Тоді (421) набирає такого вигляду:

()

∫

γ

γ==

⎟

⎠

⎞

⎜

⎝

⎛

+<<

⋅

−=

⎟

⎠

⎞

⎜

⎝

⎛

<

−

γγ

γ

t

tf

n

St

xa

n

St

xPt

n

S

ax

P

0

BB

B

,2

оскільки

()

tf

для розподілу Стьюдента є функцією парною.

Обчисливши за даним статистичним розподілом

B

x , S і визна-

чивши за таблицею розподілу Стьюдента значення

γ

t

, будуємо

довірчий інтервал

.

BB

n

St

xa

n

St

x

γγ

+<<

⋅

−

(422)

Тут

()

1, −=γ

γ

nkt обчислюємо за заданою надійністю γ і чис-

лом ступенів свободи

1

−

=

nk

за таблицею (додаток 3).

Приклад. Випадково вибрана партія з двадцяти приладів

була випробувана щодо терміну безвідказної роботи кож-

ного з них t

і

. Результати випробувань наведено у вигляді

дискретного статистичного розподілу:

t

i

100 170 240 310 380

n

i

2 5 10 2 1

З надійністю

99,0=

γ

побудувати довірчий інтервал для «а» (серед-

нього часу безвідказної роботи приладу).

Розв’язання. Для побудови довірчого інтервалу необхідно знайти

середнє вибіркове і виправлене середнє квадратичне відхилення.

Обчислимо

B

x

:

.5,222

20

4450

20

138023101024051702100

B

==

⋅

+

⋅

+

⋅

+

⋅

+⋅

==

∑

n

nt

x

ii

Отже, дістали

.год5,222

B

=x

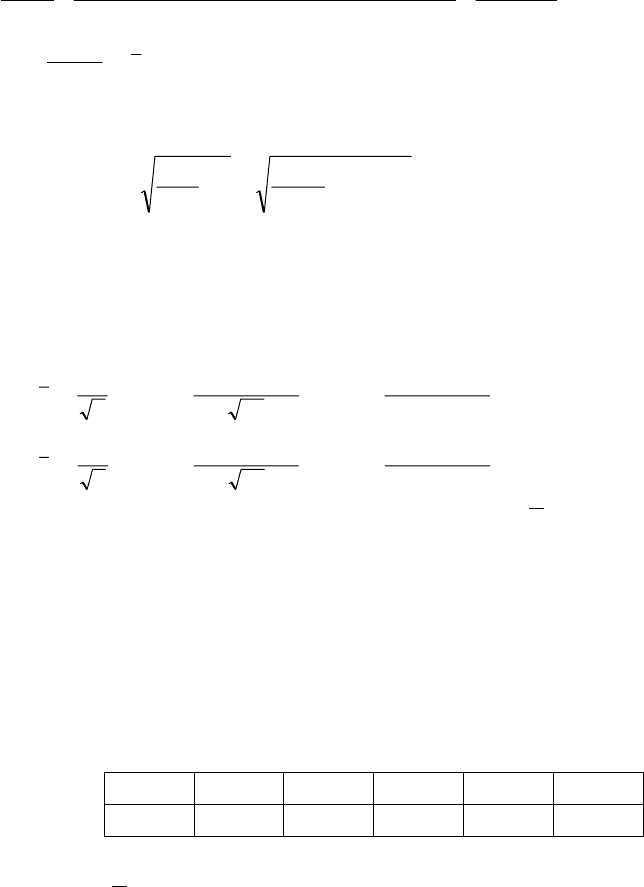
63

Визначимо D

B

:

.85553

20

1000771

20

138023101024051702100

22222

2

==

⋅+⋅+⋅+⋅+⋅

=

∑

n

nt

ii

() ( )

.75,434825,50649855535,22285553

22

B

2

B

=−=−=−=

∑

x

n

nt

D

ii

Отже, D

B

= 4348,75.

Виправлене середнє квадратичне відхилення дорівнюватиме:

.год66,6775,4348

120

20

1

B

≈⋅

−

=

−

= D

n

S

За таблицею значень

()

99,0

0

=γ=

∫

t

dtxf (додаток 3) розподілу Стью-

дента за заданою надійністю

99,0

=

γ

і числом ступенів свободи

1−= nk

= 20 – 1 = 19 знаходимо значення

(

)

===γ 19,99,0 kt .861,2

Обчислимо кінці довірчого інтервалу:

год.2,179

472,4

66,67861,2

5,222

20

66,67861,2

5,222

B

=

⋅

−=

⋅

−=−

γ

n

St

x

.год8,265

472,4

66,67861,2

5,222

20

89,67861,2

5,222

B

=

⋅

+=

⋅

+=+

γ

n

St

x

Отже, з надійністю

99,0

=

γ

можна стверджувати, що

аX =

Г

буде

міститися в інтервалі

8,2652,179

<

a .

При великих обсягах вибірки, а саме:

,30>n на підставі централь-

ної граничної теореми теорії ймовірностей (теореми Ляпунова) розпо-

діл Стьюдента наближається до нормального закону. У цьому разі

γ

t

знаходиться за таблицею значень функції Лапласа.

Приклад. У таблиці наведено відхилення діаметрів вали-

ків, оброблених на верстаті, від номінального розміру:

h

= 5 мк 0 — 5 5 — 10 10 — 15 15 — 20 20 — 25

n

i

15 75 100 50 10

Із надійністю

99,0

=

γ

побудувати довірчий інтервал для

аX =

Г

.

64

Розв’язання. Для побудови довірчого інтервалу необхідно знайти

B

x

, S.

Для цього від інтервального статистичного розподілу, наведеного в

умові задачі, необхідно перейти до дискретного, а саме:

*

i

x

2,5 7,5 12,5 17,5 22,5

n

i

15 75 100 50 10

Обчислимо

B

x

:

=====

∑

250Оскільки

*

B i

ii

nn

n

nx

x

=

⋅

+

⋅

+

⋅

+

⋅

+⋅

=

250

105,22505,171005,12755,7155,2

.8,11

250

2950

250

22587512505,5625,37

==

+

=

Отже,

.мк8,11

B

=x

Визначимо D

B

:

()

() () ( ) ( ) ( )

=

⋅+⋅+⋅+⋅+⋅

=

∑

250

105,22505,171005,12755,7155,2

22222

2

*

n

nx

ii

250

5,50625,153121562575,421875,93

+

++

=

.25,161

250

5,40312

==

()

() ( )

.01,2224,13925,1618,1125,161

22

B

2

*

B

=−=−=−=

∑

x

n

nx

D

ii

Обчислимо виправлене середнє квадратичне відхилення S:

.мк7,401,22

1250

250

1

B

≈⋅

−

=

−

= D

n

S

З огляду на великий (n = 250) обсяг вибірки можна вважати, що ро-

зподіл Стьюдента близький до нормального закону. Тоді за таблицею

значення функції Лапласа

(

)

.58,2495,0

=

→

=

γγ

ttФ

Обчислимо кінці інтервалів:

.мк03,1177,08,11

8,15

7,458,2

8,11

250

7,458,2

8,11

B

=−=

⋅

−=

⋅

−=−

γ

n

St

x

65

.мк57,1277,08,11

8,15

7,458,2

8,11

250

7,458,2

8,11

B

=+=

⋅

+=

⋅

+=+

γ

n

St

x

Отож, довірчий інтервал для середнього значення відхилень буде

таким:

57,1203,11

<

a .

Звідси з надійністю

99,0

=

γ

(99%) можна стверджувати, що

а

∈

[11,03 мк; 12,57 мк].

8. Побудова довірчих інтервалів

із заданою надійністю

γ для

Г

D ,

Г

σ

У разі, коли ознака Х має нормальний закон розподілу, для

побудови довірчого інтервалу із заданою надійністю

γ

для

гг

, σD

застосовуємо випадкову величину

,

1

2

Г

2

S

n

σ

−

=χ (423)

що має розподіл

2

χ

із

1

−

=

nk

ступенями свободи.

Оскільки випадкові події

(

)

2

22

1

χ<χ<χA

і

⎟

⎠

⎞

⎜

⎝

⎛

χ

<

χ

<

χ

2

1

22

2

111

B

є рівноймовірними, тобто їх імовірності рівні

(

)

(

)

(

)

,BPAP

=

маємо:

()

.

111

2

1

22

2

22

1

⎟

⎠

⎞

⎜

⎝

⎛

χ

<

χ

<

χ

=χ<χ<χ PP

(424)

Підставляючи в (424)

,

1

2

S

n

σ

−

=χ

дістанемо

⎟

⎠

⎞

⎜

⎝

⎛

χ

<

σ

−

<

χ

=

⎟

⎠

⎞

⎜

⎝

⎛

χ

<

χ

<

χ

2

1

2

Г

2

1

22

2

1

11111

S

n

PP

=

()

(

)

(

)

.

111

1

2

1

2

Г

2

1

2

γ=

⎟

⎠

⎞

⎜

⎝

⎛

χ

−

<σ<

χ

−

=

⎟

⎠

⎞

⎜

⎝

⎛

χ

<

−

σ

<

χ

SnSn

P

Sn

P

Г

66

Отже, довірчий інтервал для

Г

2

Г

D=σ матиме вигляд:

()

(

)

2

1

2

Г

2

11

χ

−

<<

χ

− Sn

D

Sn

. (425)

Тоді довірчий інтервал для

Г

σ

випливає із (425) і буде таким:

1

Г

2

11

χ

−

<σ<

χ

− nSnS

. (426)

Значення

2

1

χ

,

2

χ знаходимо за таблицею (додаток 4) згідно з

рівностями:

(

)

;

2

1

2

1

2

α

−=χ>χP (427)

(

)

,

2

α

=χ>χP (428)

де

γ

−

=

α 1

.

Приклад. Перевірена партія однотипних телевізорів х

і

на

чутливість до відеопрограм n

i

, дані перевірки наведено як

дискретний статистичний розподіл:

n

i

, мкв 200 250 300 350 400 450 500 550

x

i

2 5 6 7 5 2 2 1

З надійністю

99,0

=

γ

побудувати довірчі інтервали для

Г

D

,

Г

σ

.

Розв’язання. Для побудови довірчих інтервалів необхідно знайти

значення

.,

2

SS

Обчислимо значення

B

x

:

=====

∑

30якТак

B

i

ii

nn

n

nx

x

=

⋅

+

⋅

+

⋅

+

⋅

+

⋅

+

⋅

+⋅+

⋅

=

30

15502500245054007350630052502200

мкв.345

30

10350

30

55010009002000245018001250400

==

+++++++

=

Жлуктенко В. І., Наконечний С. І., Савіна С.С. Теорія ймовірностей і математична статистика: У 2-х ч. - Ч. ІІ. Математична статистика

Подождите немного. Документ загружается.