Жлуктенко В. І., Наконечний С. І., Савіна С.С. Теорія ймовірностей і математична статистика: У 2-х ч.

227

Довірчий інтервал для множинної лінійної регресії

Матриця Х містить m лінійно незалежних векторів-стовпців, а

це означає, що ранг її дорівнюватиме m і визначник

.0≠

′

XX

Отже, матриця

XX

′

має обернену.

Дисперсії статистичних оцінок

**

2

*

1

*

0

...,,,

m

ββββ

визначають з

допомогою кореляційної матриці для вектора

*

β

r

.

()()()

.

***

′

β−ββ−β=β

r

MK

Оскільки

()

(

)

,

1

EXXXX

=

′′

−

то, скориставшись (545), (547),

дістанемо

(

)

.

1

*

ε

′

+β=β

−

r

XXX

(548)

Тоді маємо

()

,

1

*

ε

′′

=β−β

−

r

XXX

(549)

()

() ( )

.

11

*

−−

′

ε=

′

ε

′′

=

′

β−β XXXXXX

rr

r

(550)

Скориставшись (549), (550), дістанемо

()()()

() ()

(

)

=

′

εε

′′

=

′

β−ββ−β=β

−− 11

***

XXXXXXXMMK

rr

r

rr

r

()() () ()()

=

′

ε

′

ε=

′′′

ε

′

ε=

−−− 111

XXMXXXXXXM

r

()()

=

′

εεε

⎟

⎠

⎞

⎜

⎝

⎛

ε

=

−1

21

2

1

...

XXM

m

()

=

′

⎟

⎠

⎞

⎜

⎝

⎛

εεεεεεε

=

−1

2

321

232

2

212

13121

2

1

...

...............

...

XXM

mmmm

m

()

(

)

(

)

()

() ( )

()()()

()

=

′

⎟

⎠

⎞

⎜

⎝

⎛

εεεεεεε

=

−1

2

321

232

2

212

13121

2

1

...

...............

...

XX

MMMM

mmmm

m

228

()

=

σ=ε=ε

==εε

=

′

⎟

⎠

⎞

⎜

⎝

⎛

σ

=

ε

−

ε

222

1

2

)()(

,0)(оскільки

...000

...............

0...00

ii

ijji

DM

KM

XX

() ( ) ()

.

1...000

...............

0...010

0...001

1

2

1

2

1

2

−

ε

−

ε

−

ε

′

σ=⋅

′

⋅⋅σ=

′

⎟

⎠

⎞

⎜

⎝

⎛

σ= XXXXIXX

Таким чином, маємо

(

)

()

1

2*

−

ε

′

σ=β XXK

r

. (551)

Оскільки

2

ε

σ

є невідомою величиною, то в (551) замість

2

ε

σ

пі-

дставляють його точкову незміщену статистичну оцінку за ана-

логією з (513).

(

)

,

1

2

−

ε

=

∑

∗

ε

mn

S

i

(552)

де n є кількістю спостережень, а m — кількістю оцінюваних

параметрів множинної лінійної регресії.

Значення дисперсії для

*

i

β

(

)

mi

K

,3,2,1,0

=

обчислюють за

формулою

,

22

*

ii

CSS

i

ε

β

=

(553)

де

ii

C

— діагональний елемент матриці

()

.

1−

′

XX

Розглянемо рівняння лінійної множинної регресії з парамет-

рами

*

i

β

()

mi ...,,3,2,1,0=

, знайденими за результатами вибірки

,...

*

2

*

21

*

1

*

0

*

mmi

xxxy β++β+β+β=

де

*

i

y

— лише одне з можливих значень прогнозної величини

для заданих значень

i

x

.

Ураховуючи те, що

*

i

β

(

)

mi

K

,3,2,1,0

=

є випадковими вели-

чинами, то

*

i

y

буде також випадковою, а тому матиме дисперсію.

Отже,

(

)

(

)

....

*

2

*

21

*

1

*

0

*

mmi

xxxDyD β++β+β+β=

229

Використовуючи властивості дисперсії від суми залежних випа-

дкових величин (випадкові величини

i

β

є залежними), дістанемо:

()

(

)

=β++β+β+β=

mmi

xxxDyD

*

2

*

21

*

1

*

0

*

...

(

)()

(

)

(

)

(

)

...2...

*

2

*

01

*2*

2

*

1

2

1

*

0

+ββ+β++β+β+β KxDxDxDxD

mm

()

(

)

(

)

...2...22...

**

11

*

2

*

121

**

0

+ββ++ββ+ββ+

mmmm

KxxKxxKx

(

)

(

)

,2...

***

11

xKxKxx

mmmm

r

β

′

=ββ+

−−

оскільки це є квадратична форма, яку можна записати у вектор-

но-матричній формі.

Отже, маємо

(

)

(

)

xKxyD

i

r

**

β

′

=

. (554)

Тоді, використовуючи (551), дістанемо

(

)

()

xXXxyD

i

r

1

2*

−

ε

′′

σ=

. (555)

Оскільки

2

ε

σ

— невідома величина, то в (555) використовуємо

її точкову незміщену статистичну оцінку

.

2

ε

S

Таким чином, маємо:

(

)

()

.

1

2*

xXXxSyD

i

r

−

ε

′′

⋅=

(556)

Отже, істинне значення Y перебуватиме в інтервалі:

() ( ) () ( )

,,,

1

*

1

*

xXXxSktyyxXXxSkty

rrrr

−

ε

−

ε

′′

γ+<<

′′

γ−

(557)

який називають довірчим.

()

kt ,γ

є випадковою величиною, що має розподіл Стьюдента з

1−−= mnk

ступенями свободи і обчислюється за таблицею (до-

даток 7) за заданою надійністю γ та числом ступенів свободи k.

Якщо до значень

i

y

— прогнозне значення — додати можливі

відхилення ознаки Y від функції регресії, то до дисперсії

()

*

yD

необхідно додати дисперсію випадкової величини

i

ε

—

,

2

ε

σ

тоб-

то його точкову незміщену статистичну оцінку

.

2

ε

S

У цьому разі

()()

xXXxSS

y

r

1

22

1

−

ε

′′

+=

. (558)

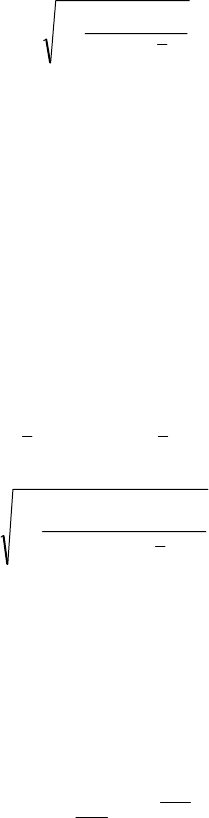
І довірчий інтервал тепер дорівнюватиме:

(

)

(

)

.,,

**

yy

SktyySkty γ+<<γ−

(559)

230

Коефіцієнт множинної регресії

Тісноту між ознаками Y та X, де

(

)

m

xxxX ...,,

21

=

, вимірюють

з допомогою коефіцієнта множинної кореляції R, що є узагаль-

ненням парного коефіцієнта кореляції r

ij

і обчислюється за фор-

мулою

()

∑

−

ε

−=

2

1

yy

R

i

. (560)

Чим ближче значення R до ±1, тим краще вибрано функцію

регресії

(

)

....,,,

21 m

xxxy

α

=

Оскільки

∑

εε

′

=ε

r

2

i

, то

(

)

(

)

=β−β−

′

=εε

′

=ε

∑

**2

r

XyXy

i

()

() ()

=β

′

β+

′

β−

′

=

***

2

r

rr

XXyXyy

()

() ()

=

′

β+

′

β−

′

= yXyXyy

r

rr

**

2

()

,

*

yXyy

r

rr

′

β−

′

=

оскільки

() ()

.

****

yXXX

r

′

β=β

′

β

При цьому

() ()

∑∑

−=− ,

2

ynyyy

ii

а оскільки

() ()

∑

′

= ,

2

yyy

i

rr

то остаточно маємо

()

() ()

2

**

1

ynyy

yXyy

R

−

′

β−

′

−=

rr

r

rr

. (561)

Нормування коефіцієнтів регресії

Множинна лінійна регресія дає змогу порівняти вплив на дос-

ліджуваний процес різних чинників. У загальному випадку змінні

i

x

репрезентують чинники, що мають різні одиниці виміру (кіло-

грами, гривні, метри тощо). Отже, для того щоб порівняти і

з’ясувати відносну вагомість кожного з чинників, використову-

ють так звані нормовані коефіцієнти регресії, які визначають за

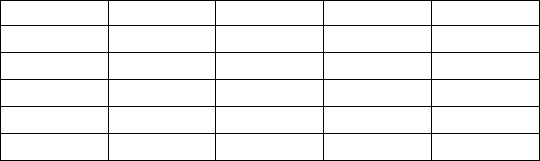
формулою

y

x

jj

S

a

j

**

β=

(

)

,,1 mj =

(562)

231

де

j

a

— коефіцієнт регресії після нормування;

j

x

S

— виправ-

лене середнє квадратичне відхилення змінної

;

j

x

y

S

— виправ-

лене середнє квадратичне відхилення ознаки Y.

Приклад 1. Ознака Y — лінійно залежна від

1i

x

,

2i

x

,

3i

x

.

Результати спостережень наведено в таблиці:

i у

і

х

і1

х

і2

х

і3

1 6 1 1 2

2 8 2 2 1

3 14 1 0 0

4 20 3 2 1

5 26 5 2 2

Необхідно:

1) знайти компоненти вектора і побудувати лінійну

⎟

⎠

⎞

⎜

⎝

⎛

β

=β

*

3

*

2

*

1

*

0

*

функцію регресії ;...

3

*

32

*

21

*

1

*

0

iiii

xxxy β++β+β+β=

2) обчислити R;

3) побудувати довірчий інтервал із надійністю

95,0

=

γ

для

множинної лінійної функції регресії та визначити дисперсії

для

*

3

*

2

*

1

*

0

,,,

ββββ

і оцінити ефективність впливу на ознаку

Y незалежних змінних

1

i

x

,

2

i

x

,

3

i

x

.

Розв’язання. 1. З умови задачі маємо:

,

2251

1231

0011

1221

2111

⎟

⎠

⎞

⎜

⎝

⎛

=X

.

26

20

14

8

6

⎟

⎠

⎞

⎜

⎝

⎛

=y

r

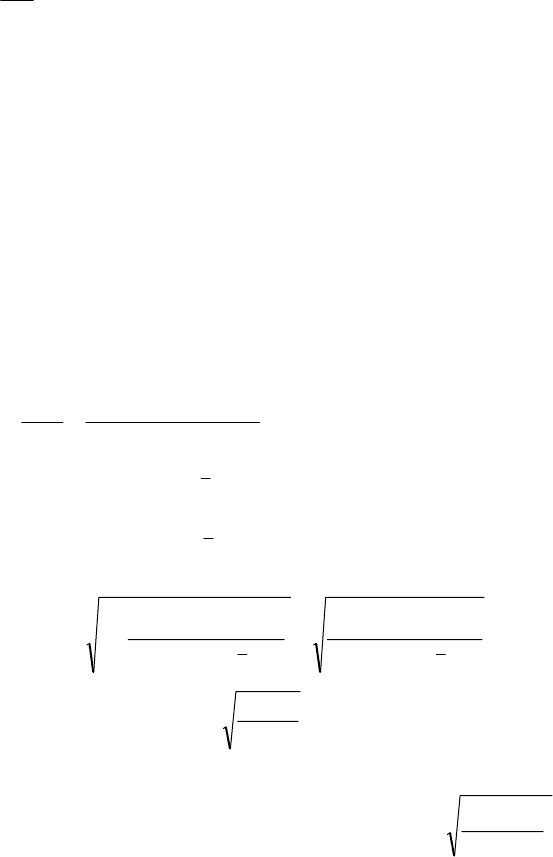
Оскільки

()

=

′′

=

⎟

⎠

⎞

⎜

⎝

⎛

β

=β

−

yXXX

r

1

*

3

*

2

*

1

*

0

*

232

.

58,2

78,3

34,6

98,7

26

20

14

8

6

21012

22021

53121

11111

9135841

351233839

8383214

413914173

178

1

⎟

⎠

⎞

⎜

⎝

⎛

−

=

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

−−−

=

Отже, дістали:

;98,7

*

0

=β

;34,6

*

1

=β

;78,3

*

2

−=β .58,2

*

3

−=β

Рівнянням регресії буде

.58,278,334,698,7

321

*

iiii

xxxy −−+=

2. Знайдемо R. Для цього необхідно визначити

()

;38,1354

26

20

14

8

6

21012

22021

53121

11111

58,278,334,698,7

*

=

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

−−=

′

β yX

r

;8,14

5

26201486

=

++++

==

∑

n

y

i

r

(

)

(

)

;2,10958,145

22

==yn

r

() ()

;8,2762,10951372

2

=−=−

′

ynyy

rr

()

.18,2592,109538,1354

2

*

=−=−

′

β ynyX

r

Тоді

()

() ()

()

=

−

′

−

′

β

=

−

′

β−

′

−=

2

*

2

*

1

ynyy

ynyX

ynyy

yXyy

R

rr

r

rr

r

rr

.968,0

8,276

18,259

==

Для побудови довірчого інтервалу для множинної лінійної функ-

ції регресії необхідно обчислити

.

ε

S

Оскільки

,

1

2

−−

ε

=

∑

ε

mn

S

i

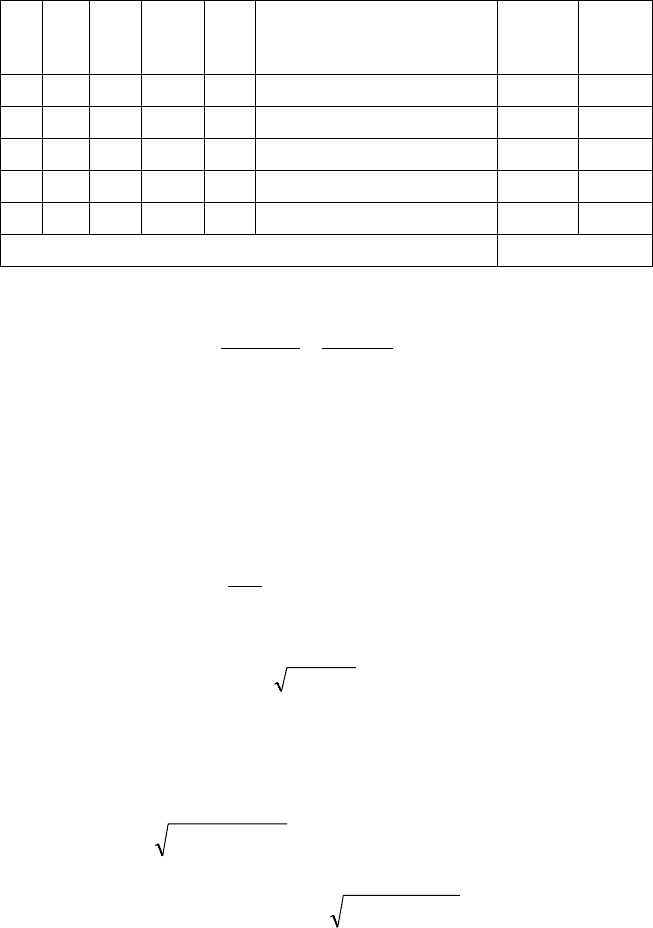
то в

цьому разі результати обчислень зручно подати у вигляді таблиці:

233

i

y

1i

x

2i

x

3i

x

321

*

58,278,334,6

98,7

iii

i

xxx

y

−−+

+=

*

ii

yy −

()

2

*

i

ε

1 6 1 1 2 5,38 0,62 0,3844

2 8 2 2 1 10,52 –2,52 6,3504

3 14 1 0 0 14,32 –0,32 0,1024

4 20 3 2 1 16,86 3,14 9,8596

5 26 5 2 2 26,96 –0,96 0,9216

618,17

2

=

∑

ε

i

Таким чином, дістанемо:

(

)

.618,17

135

618,17

1

2

*

2

=

−−

=

−−

ε

=

∑

ε

mn

S

i

Візьмемо

;2

1

=x ;6

2

=

x 10

3

=

x

і обчислимо

.82,271058,2678,3234,698,7

−

=

⋅

−

⋅

−

⋅

+=

i

y

Знайдемо

(

)

()

=

′

=

−

ε

xXXxSyD

i

r

1

2*

()

.992,683

10

6

2

1

9135843

351233839

8383214

413914173

178

1

10621618,17 =

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

−−−

⋅=

.15,26992,683

*

≈=

y

S

Для побудови довірчого інтервалу знаходимо

()

(

)

()

.706,121,95,0

135,95,01,95,0

===γ=

=−−==γ=−−==γ

kt

ktmnkt

Тоді

() ( )

.262,33215,26706,12,

1

=⋅=⋅

′′

γ

−

ε

xXXxSkt

rr

І довірчий інтервал дорівнюватиме

() ( )

→⋅

′′

⋅γ±=

−

ε

xXXxSktyy

ii

rr

1

*

,

.242,30428,360

<

−

→

i

y

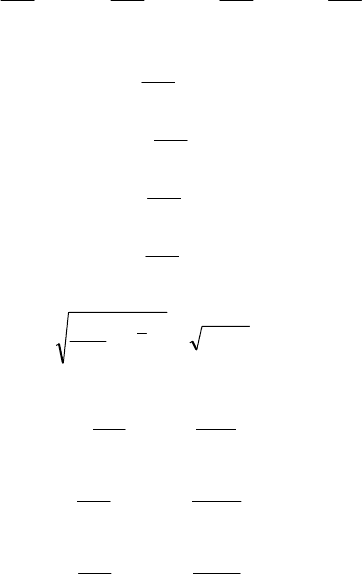
234

Оскільки діагональні елементи матриці

()

1

−

′

XX

відповідно

дорівнюють

;

178

173

11

=b

;

178

32

22

=b

;

178

123

33

=b

,

178

91

44

=b

то відповідно дістанемо

,123,17

178

173

618,17

11

22

*

0

=⋅==

ε

β

bSS ;138,4

*

0

=

β

S

,167,3

178

32

618,17

22

*

1

=⋅==

ε

β

bSS

;78,1

*

1

=

β

S

,17,12

178

123

618,17

33

22

*

2

=⋅==

ε

β

bSS ;489,3

*

2

=

β

S

,007,9

178

91

618,17

44

22

*

3

=⋅==

ε

β

bSS .001,3

*

3

=

β

S

Обчислимо

()

.44,736,53

2

≈=−

′

= y

n

yy

S

y

r

Визначимо нормовані коефіцієнти регресії:

,52,1

44,7

78,1

34,6

*

1

*

11

=⋅=β=

β

y

S

a

,77,1

44,7

489,3

78,3

*

2

*

22

−=⋅−=β=

β

y

S

a

.04,1

44,7

001,3

58,2

*

3

*

33

−=⋅−=β=

β

y

S

a

Отже, для змінної

12

x

вплив на ознаку Y є найефективнішим

порівняно з дією змінних

,

1i

x .

3i

x

4. Нелінійна регресія

Якщо в рівняння множинної регресії змінні

ij

x

входять як

n

ij

x

,

то регресія називається нелінійною.

У загальному випадку нелінійна регресія записується в такому

вигляді:

,...

3

33

2

22110

i

m

mmii

xxxxy ε+β++β+β+β+β=

(569)

235

де параметри

m

βββββ ...,,,,

3210

є сталими невідомими вели-

чинами, які підлягають статистичним оцінкам, а

i

ε

— випадкова

величина, яка має нормальний закон розподілу з числовими ха-

рактеристиками

()

,0

=

ε

i

M

(

)

(

)

,

22

ε

σ=ε=ε

ii

MD

і при цьому випад-

кові величини

m

εεε ...,,

21

між собою не корельовані. Реалізуючи

вибірку обсягом n, згідно з (563), дістанемо систему нелінійних

рівнянь виду:

....

..............................................................................

.............................................................................

;...

**2

3

*

3

2

*

21

*

1

*

0

*

33

*2

33

*

3

2

32

*

231

*

1

*

03

*

22

*2

23

*

3

2

22

*

221

*

1

*

02

*

11

*2

13

*

3

2

12

*

211

*

1

*

01

n

m

nmmnnnn

m

mm

m

mm

m

mm

xxxxy

ε+β++β+β+β+β=

(564)

Систему (564) можна подати у векторно-матричній формі так:

,

**

ε+β=

r

Xy

(565)

де

,

...

3

2

1

⎟

⎠

⎞

⎜

⎝

⎛

=

n

y

r

,

...1

..................

...1

3

2

1

2

33

2

3231

2

22

2

2221

1

2

22

2

1211

⎟

⎠

⎞

⎜

⎝

⎛

=

m

nmnnn

m

xxxx

X

,

...

*

3

*

2

*

1

*

0

*

⎟

⎠

⎞

⎜

⎝

⎛

β

=β

m

r

.

...

*

3

*

2

*

1

*

⎟

⎠

⎞

⎜

⎝

⎛

ε

=ε

n

r

Тут

m

βββββ ...,,,,

3210

є випадковими величинами, які визна-

чаються шляхом обробки результатів вибірки і є точковими не-

зміщеними статистичними оцінками відповідних параметрів рів-

няння (563), а саме:

....,,,,

3210 m

βββββ

Здійснивши аналогічні перетворення, які були зроблені для

лінійної множинної регресії, дістанемо:

()

yXXX

r

′′

=β

−

1

*

. (566)

Тіснота зв’язку вимірюється з допомогою кореляційного від-

ношення

()

∑

−

ε

−=η

2

*

1

yy

i

r

, (567)

10

≤

η

≤

.

236

Приклад 2. Результати спостережень над ознаками Х і Y

наведено у таблиці:

i х

і

у

і

1 1 8

2 2 4

3 4 2

4 6 1

5 8 0

6 10 6

7 12 8

8 14 10

Потрібно:

1) визначити точкові незміщені статистичні оцінки для па-

раметрів нелінійної регресії

;

2

210

xxy

ii

β+β+β=

2) обчислити η.

Розв’язання. З результатів вибірки маємо:

;

196141

144121

100101

6481

3661

1641

421

111

⎟

⎠

⎞

⎜

⎝

⎛

=X

.

10

8

6

0

1

2

4

8

⎟

⎠

⎞

⎜

⎝

⎛

=y

r

Використовуючи (566), дістанемо:

×

⎟

⎠

⎞

⎜

⎝

⎛

−

−−

−

=

⎟

⎠

⎞

⎜

⎝

⎛

β

=β

120129

59

40043

289

40043

680

40043

289

840903

94613

280301

82843

40043

680

280301

82843

280301

291499

*

2

*

1

*

0

*

r

Жлуктенко В. І., Наконечний С. І., Савіна С.С. Теорія ймовірностей і математична статистика: У 2-х ч. - Ч. ІІ. Математична статистика

Подождите немного. Документ загружается.