Жлуктенко В. І., Наконечний С. І., Савіна С.С. Теорія ймовірностей і математична статистика: У 2-х ч.

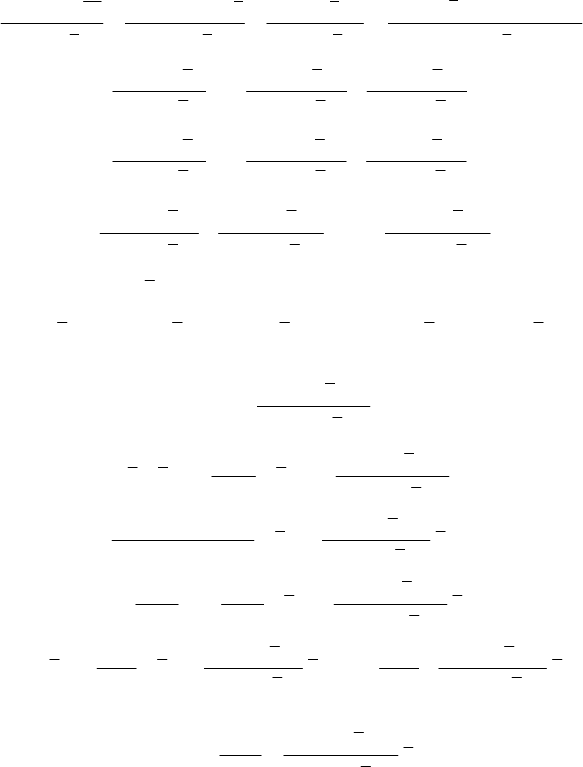
197

Якщо параметри

10

,

β

рівняння (486) — сталі величини, то

*

1

*

0

, ββ

, які обчислені шляхом обробки реалізованої вибірки, є ви-

падковими величинами і виконують функцію точкових статисти-

чних оцінок для них.

2.2. Властивості

**

10

β,β .

Точкові статистичні оцінки

*

1

*

0

, ββ

можна подати в такому вигляді:

() ()

(

)

()

=

−

=

−

=

−

=β

∑

∑∑

∑

222

*

1

xx

yxx

xx

xyyx

xx

yxnyx

i

ii

i

iii

i

ii

(

)

(

)

()

=

−

ε+β+β−

∑

2

10

xx

xxx

i

iii

()

(

)

()

(

)

()

=

−

ε

−

+

−

β+

−

β=

∑

22

1

2

0

xx

xxx

xx

i

ii

i

ii

i

()

(

)

()

=

−

ε−

+

−

β+

−

β=

∑

22

2

1

2

0

xx

xxx

xx

i

ii

i

ii

i

()

.

2

1

22

2

1

∑

−

ε−

+β=

−

ε−

+

−

β=

xx

i

ii

i

ii

i

Оскільки

(

)

∑

=

− ,0xx

i

()

(

)

.

2

222

∑∑∑∑∑∑

−=−=−=−=− xxxnxxxxxxxxxx

iiiiiiii

Отже, дістали:

(

)

()

.

2

1

*

1

∑

−

ε−

+β=β

xx

i

ii

(499)

()

=

⎟

⎠

⎞

⎜

⎝

⎛

−

ε−

+β−=β−=β

∑

∑∑

2

1

*

1

*

0

xx

x

n

y

xy

i

iii

()

(

)

()

=

−

ε

−

−β−

ε

+

β

+

β

=

∑

x

xx

x

n

x

i

iiii

2

1

10

(

)

()

=

−

ε−

−β−

ε

+β+β=

∑

x

xx

x

nn

x

i

iiii

2

110

(

)

()

(

)

()

.

2

0

2

110

x

xx

n

x

xx

x

n

x

i

iii

i

iii

∑

−

ε

−

ε

+β=

−

ε

−

−β−

ε

+β+β=

Остаточно маємо:

(

)

()

x

xx

n

i

iii

2

0

*

0

∑

−

ε−

−

ε

+β=β

. (500)

198

Знаходимо числові характеристики для випадкових величин

:,

*

1

*

0

ββ

а) основні числові характеристики для

*

0

β

()

=

⎟

⎠

⎞

⎜

⎝

⎛

−

ε−

−

ε

+β=β

∑

∑∑

x

xx

n

MM

i

iii

2

0

*

0

()

=

⎟

⎠

⎞

⎜

⎝

⎛

−

ε−

−

⎟

⎠

⎞

⎜

⎝

⎛

ε

+β=

∑

∑∑

x

xx

M

n

MM

i

iii

2

0

(

)

(

)

(

)

()

()()

.0.

0

2

0

=εβ=

−

ε−

−

ε

+β=

∑

i

iii

M

xx

Mxx

n

M

Отже, ми довели, що

*

0

β

є точковою незміщеною статистич-

ною оцінкою для параметра

0

β

,

()

=

⎟

⎠

⎞

⎜

⎝

⎛

−

ε−

−

ε

+β=β

∑

∑∑

x

xx

n

DD

i

iii

2

0

*

0

()

=

⎟

⎠

⎞

⎜

⎝

⎛

−

ε−

−−

⎟

⎠

⎞

⎜

⎝

⎛

ε

+β=

∑

∑∑

x

xx

D

n

DD

i

iii

2

0

()

()()

()

[]

=

−

ε−

+

ε

=

∑

∑∑

2

xx

Dxx

x

n

D

i

iii

()

()()

()

[]

=

−

ε−

+

ε

=

∑

∑∑

2

xx

Dxx

x

n

D

i

iii

()

=σ

−

+

σ

=

ε

∑

2

xx

x

n

i

()

=

⎟

⎠

⎞

⎜

⎝

⎛

−

+

σ

=

−

σ

+

σ

=

∑∑

εεε

2

1

xx

nx

n

xx

x

n

ii

()()

()

() ()

.

2

22

2

22

2

22

2

∑

−

σ

=

−

+−σ

=

−

+−

⋅

σ

=

εεε

xx

x

n

xx

xnxnx

n

xx

nxxx

n

i

Далі маємо:

()

2

*

0

ε

σ

−

=β

∑

xxn

x

D

i

, (501)

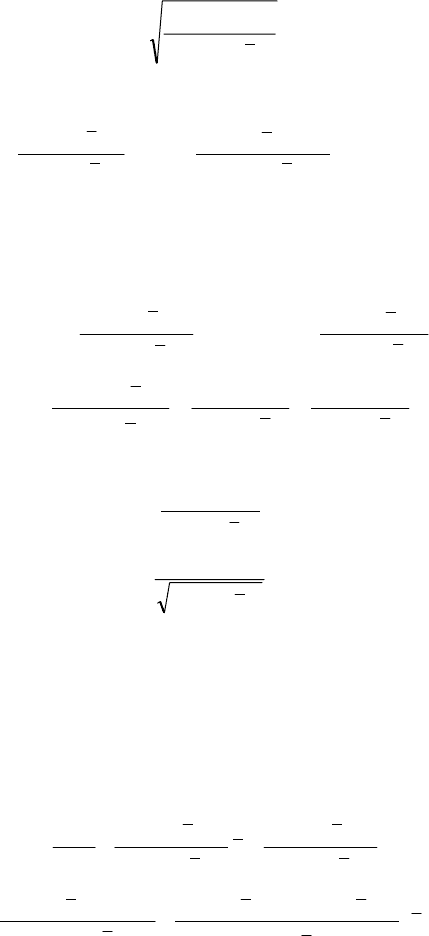
199

()

ε

σ

−

=βσ

∑

2

*

0

xxn

x

i

. (502)

б) Основні числові характеристики для параметрів

*

i

β

=

⎟

⎠

⎞

⎜

⎝

⎛

−

ε−

+β

∑

2

1

)(

xx

M

i

ii

(

)

(

)

()

()()

.0.

1

2

1

=εβ=

−

ε

−

+β

∑

i

ii

M

xx

Mxx

Отже, визначили, що

*

1

β

є точковою незміщеною систематич-

ною оцінкою для параметра

1

β

(

)

1

*

1

β=βM

. (503)

()

=

⎟

⎠

⎞

⎜

⎝

⎛

−

ε−

+β=β

∑

2

1

*

1

xx

DD

i

ii

()

=

⎟

⎠

⎞

⎜

⎝

⎛

−

ε−

+β

∑

2

1

xx

DD

i

ii

()

(

)

()

[]

(

)

()()

.

2

22

2

∑∑

∑

−

σ

=

−

ε

=

−

ε=

ε

xxxx

D

xx

D

ii

i

Звідси маємо:

()

,

2

*

1

∑

−

σ

=β

ε

xx

D

i

(504)

()

.

2

*

1

∑

−

σ

=βσ

ε

xx

i

(505)

Статистичні оцінки

*

1

*

0

, ββ як випадкові величини впливають

на зміщення лінії регресії; так,

*

0

β викликає вертикальне зміщен-

ня лінії регресії, а

*

1

β — зміну кута нахилу її.

З’ясуємо, чи існує кореляційний зв’язок між випадковими ве-

личинами

*

1

*

0

, ββ .

(

)

(

)

=β−ββ−β=

ββ

1

*

10

*

0

*

1

*

0

MK

()

=

⎟

⎠

⎞

⎜

⎝

⎛

−

ε−

⋅

⎟

⎠

⎞

⎜

⎝

⎛

−

ε−

−

ε

=

∑

∑∑

22

xx

x

xx

n

M

i

ii

i

iii

()

() ()

()

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

ε−⋅ε−

−

ε⋅ε−

=

∑

∑∑

∑

∑∑

x

xx

xxxx

xxn

xx

M

i

iiii

i

iii

2

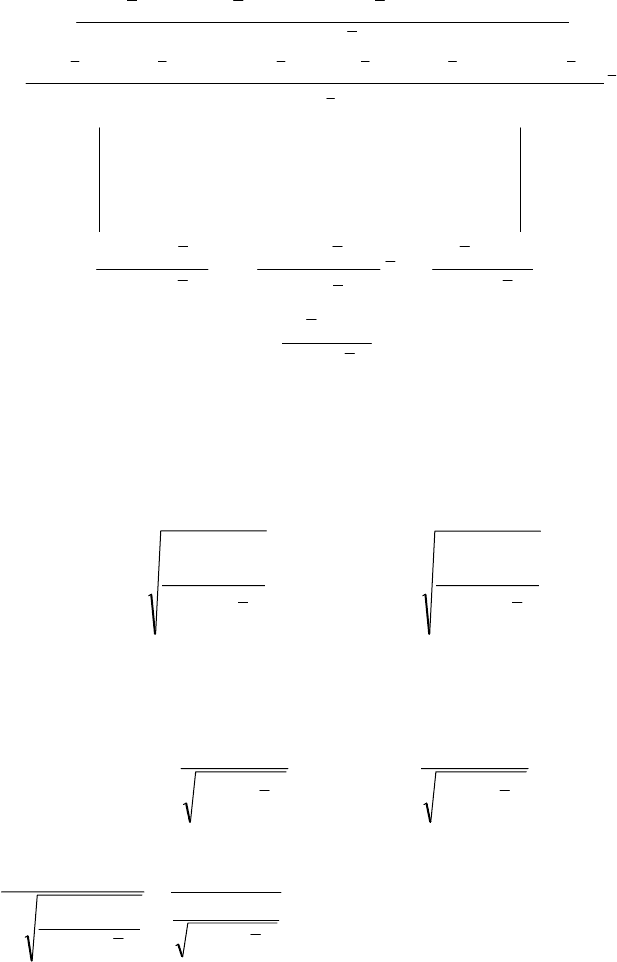
200

()() ()

[]

[

]

()

−

⎟

⎠

⎞

⎜

⎝

⎛

−

ε++ε+εε−++ε−+ε−

=

∑

2

212211

......

xxn

xxxxxx

M

i

nnn

()()

(

)

[]

(

)

(

)

(

)

[

]

()

=

∑

−

ε−

+

ε

−

+

ε

−

ε

−

+

+ε−+ε

−

− x

xx

xxxxxxxxxxxx

M

i

nnnn

2

22112211

......

(

)

(

)

()

=

=σ=ε

=

εε

=

ε

=

ε

=

ε

constмаємо

притодінулеві,дорівнюютьсподівання

іматематичнікореляціявідсутняіміж

бо,0,0оcкільки

22

i

ji

iji

M

ji

MM

()

(

)

()

;

2

∑

−

σ⋅

−=

−

σ−

−σ

−

=

εε

ε

xx

x

xx

xxn

xx

i

()

.

2

*

1

*

0

∑

−

σ⋅

−=

ε

ββ

xx

x

K

i

(506)

Відповідно до (499), (500)

**

10

, ββ

містять як складову випад-

ковий компонент

i

ε

з нормальним законом розподілу ймовірнос-

тей. Звідси випливає:

*

0

β

матиме нормальний закон розподілу із числовими характе-

ристиками:

,

0

β

=

a

()

,

1

2

1

ε

σ

−

=σ

∑

=

n

i

n

xxn

x

тобто

()

;;

1

2

1

0

⎟

⎠

⎞

⎜

⎝

⎛

σ

−

β

ε

∑

=

n

i

n

xxn

x

N

*

1

β

також буде мати нормальний закон розподілу з числовими

характеристиками

,

1

β=a

()

,

1

2

∑

=

−

σ

=σ

n

i

xx

тобто

()

.;

1

2

1

⎟

⎠

⎞

⎜

⎝

⎛

−

σ

β

∑

=

n

i

xx

N

Тоді

()

∑

−

σ

β−β

ε

2

1

0

*

0

xxn

x

i

і

()

∑

−

σ

β−β

ε

2

1

*

1

xx

i

матимуть закон розподілу N(0; 1).

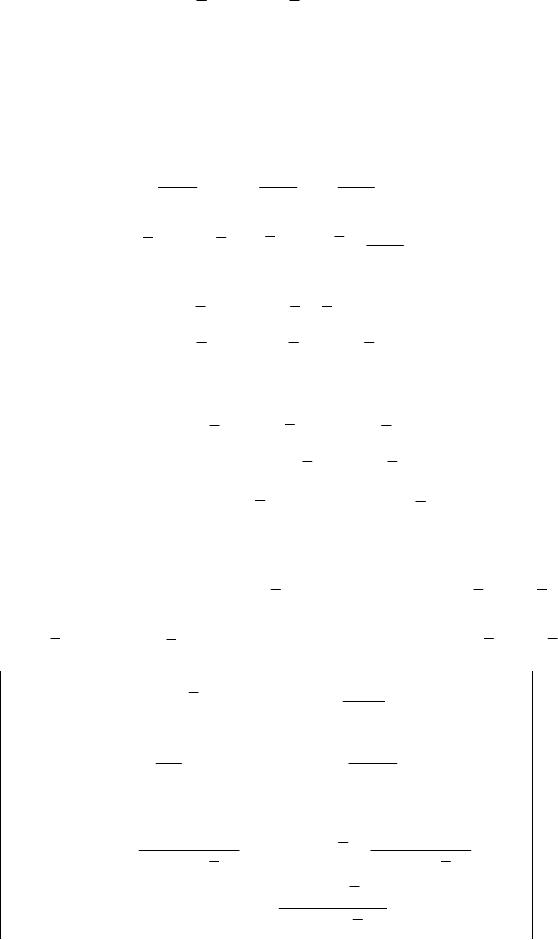
201

Рівняння регресії можна подати в такому вигляді:

(

)

.

**

1 iii

xxyy ε=−β=−

(507)

Розглянемо модель (486)

,

0 iiii

xy

ε

+

β

+

β

=

(508)

яку подамо через середні величини:

()

(

)

∑∑∑∑

→ε+β+β=ε+β+β=

iiiiiii

xnxy

00

→

ε

+β+β=→

∑∑∑

nn

x

n

y

iii

10

ε

+

β

+

β

=

→

10

xy

(тут

n

i

∑

ε

=ε ).

Отже, дістали

→

⎩

⎨

⎧

ε+β+β=

ε

+

β

+

β

=

,

0

xy

i

iiii

(509)

(

)

(

)

ε

−

ε

+

−

β

=

−

iii

xxyy

1

=

∗

ε

i

. (510)

Ураховуючи (507) і (510),

*

i

ε

можна подати так:

(

)

(

)

(

)

→−β−ε−ε+−β=ε xxxx

iiii

*

11

*

(

)

()()

.

1

*

1

*

ε−ε+−β−β−=ε→

iii

xx

(511)

А тому

()

(

)

()

[

]

2

1

*

1

2

∑∑

−β−β−ε−ε=ε

∗

xx

iii

.

Тоді

()

(

)

=ε

∑

∗

2

i

M

()

(

)

()()

(

)

=ε−ε−β−β−−β−β+ε−ε=

∑∑∑

iiii

xxxxM

1

*

1

2

1

*

1

2

()

(

)

−β−β−+ε−ε=

∑∑

2

1

*

1

22

MxxM

ii

(

)

()()

[

]

=ε−ε−β−β

∑

ii

xxM

1

*

1

()

()()

() ()

()

=

−

ε−

=β−β

σ=

−

σ

−→

−

σ

=β−β

=εεσ=ε

σ−=

σ

−σ=ε−ε=

=

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

ε

−ε=ε−ε

=

∑

∑∑

∑

ε

εε

ε

одержимо,

)(

що,враховуючи

;

;0,оскільки

,1

1

2

1

*

1

2

1

*

1

22

2

22

2

xx

M

MM

n

nM

n

M

n

MM

i

ii

i

jii

ii

i

ii

202

(

)

()()

(

)

()

() ()

[]

()

[]

()

()()

()

.

0Тут.

2

1

*

1

∑

∑∑

∑

=−σ=

−

ε−

=

=ε−−

−

ε−

=

⎟

⎠

⎞

⎜

⎝

⎛

ε−−ε−⋅

−

ε−

=ε−ε−β−β

=

ε

xx

Mxx

xx

M

xxxx

xx

М

xxM

i

ii

i

ii

iii

i

ii

Отже, дістали

()

(

)

() ( )

.221

2222

2

*

εεεε

σ−=σ−σ+σ−=ε

∑

nnM

i

Звідси маємо

(

)

.

2

−

⎟

⎠

⎞

⎜

⎝

⎛

ε

=σ

∑

∗

ε

n

M

i

(512)

(

)

2

ε

∗

=

−

ε

∑

S

n

i

(513)

є точковою незміщеною статистичною для

.

2

ε

σ

Далі, враховуючи (513), дістанемо:

()

,

2

*

0 ε

∑

−

=β S

xxn

x

D

n

i

n

i

(514)

()

,

2

*

0 ε

∑

−

=βσ S

xxn

x

n

i

n

i

(515)

()

,

2

*

1

∑

−

=β

ε

n

i

xx

S

D

(516)

()

,

2

*

1

∑

−

=βσ

ε

n

i

xx

S

(517)

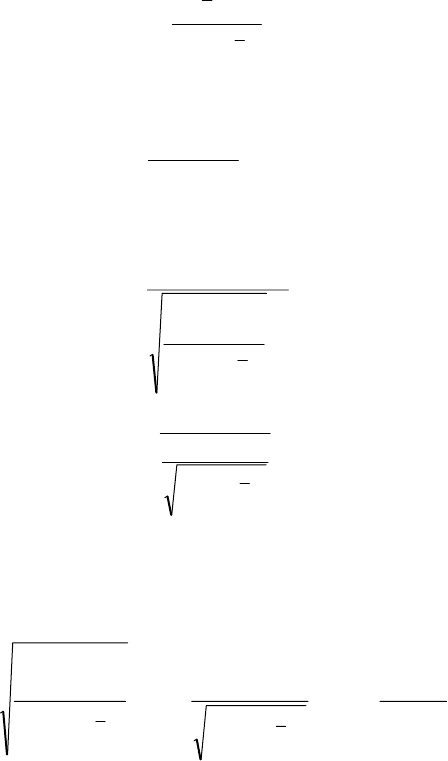
203

()

.

2

*

1

*

0

∑

−

−=

ε

ββ

n

i

xx

Sx

K

(518)

З наведених вище перетворень можна зробити висновок, що:

випадкова величина

(

)

2

χ=

σ

−

ε

Sn

(519)

матиме розподіл

2

χ

із

2

−

=

nk

ступенями свободи;

випадкові величини:

()

ε

∑

−

β−β

=

S

xxn

x

t

n

i

n

i

2

0

*

0

; (520)

()

∑

−

β−β

=

ε

n

i

xx

S

t

2

0

*

1

матимуть розподіл Стьюдента (t-розподіл) із

2

−

=

nk ступенями

свободи.

Ураховуючи (519), (520) ми дійшли висновку, що

*

2

*

1

*

0

x

β+β

буде мати двовимірний нормальний закон на площині, а саме:

()

.;;;;

*

1

*

0

*

1

*

0

*

1

*

0

2

1

2

1

0

⎟

⎠

⎞

⎜

⎝

⎛

σσ

=

−

σ

βσ

−

β

ββ

ε

ββ

ε

∑

K

r

xx

xxn

x

N

i

Скориставшись (519), (520) для параметрів

*

1

*

0

,

ββ

парної лі-

нійної функції регресії, ми зможемо побудувати довірчі інтерва-

ли із заданою надійністю γ, а також перевірити значущість кое-

фіцієнтів лінійної регресії.

2.3. Перевірка значущості коефіцієнтів лінійної регресії.

Ґрунтуючись на значеннях дисперсій

*

1

*

0

, ββ

, можна перевірити

значущість цих коефіцієнтів на заданому рівні

,05,0

=

α

викорис-

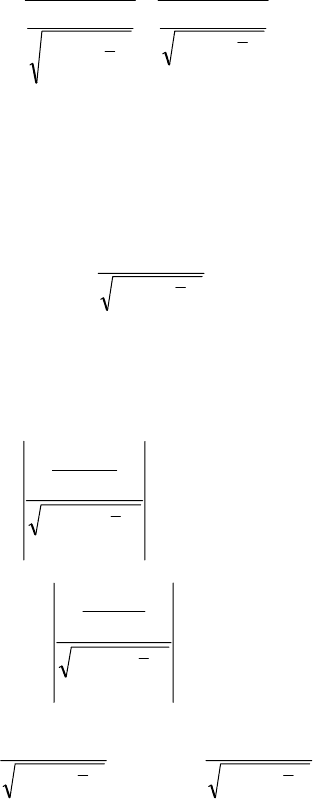
204

товуючи при цьому відому схему перевірки правильності нульо-

вої гіпотези Н

0

. У парній лінійній регресії, як правило, на значу-

щість перевіряється коефіцієнт

1

β

.

Нульова гіпотеза має вигляд Н

0

:

0

1

=

β

. За статистичний кри-

терій беремо випадкову величину

()

,

2

*

1

2

0

*

1

∑

−

β

=

−

β−β

=

εε

xx

S

xx

S

t

i

що має t-розподіл із

2

−

=

nk

ступенями свободи (розподіл Стью-

дента).

При альтернативній гіпотезі

α

H :

0

1

<

β

— лівобічна критична

область і при

αH

:

0

1

≠

β

— двобічна критична область.

Спостережуване значення критерію обчислюється як

()

.

2

*

1

*

∑

−

β

=

xx

t

i

2.4. Довірчі інтервали для

*

1

*

0

β,β .

Побудова довірчого інте-

рвалу для параметра

*

1

β

із заданою надійністю γ здійснюється ви-

користовуючи (520). Отже, маємо:

()

,,

2

1

*

1

γ=

⎟

⎠

⎞

⎜

⎝

⎛

γ<

−

β−β

γ

ε

∑

kt

xx

S

P

i

()

→γ=

⎟

⎠

⎞

⎜

⎝

⎛

γ<

−

β−β

<γ

γ

ε

γ

∑

kt

xx

S

ktP

i

,,

2

1

*

1

()

γ=

⎟

⎠

⎞

⎜

⎝

⎛

−

γ

+β<β<

−

γ

−β→

∑∑

εε

2

*

11

2

1

,,

xx

Skt

xx

Skt

P

ii

.

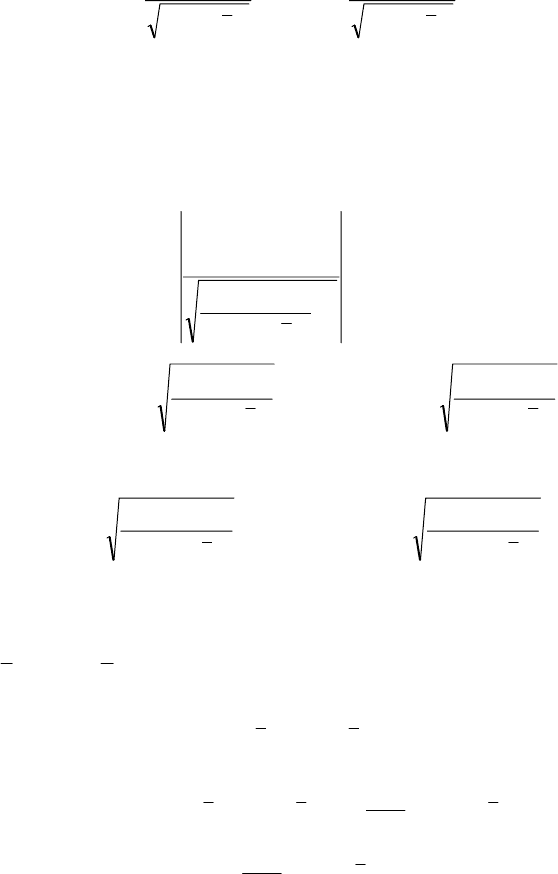
205

Отже, довірчий інтервал для параметра

1

β

буде

()

(

)

()

,

,,

2

11

2

1

∑∑

−

γ

+β<β<

−

γ

−β

ε

∗

ε

∗

xx

Skt

xx

Skt

ii

(521)

де

(

)

kt ,γ

знаходимо за таблицею (додаток 3) за заданою надій-

ністю γ і числом ступенів свободи

2

−

=

nk

;

Побудова довірчого інтервалу для параметра

*

0

β

із заданою

надійністю γ.

Аналогічно скориставшись (520), маємо

()

→γ=

⎟

⎠

⎞

⎜

⎝

⎛

γ<

−

β−β

ε

∑

kt

S

xxn

x

P

i

,

2

0

*

0

()

.,,

2

*

00

2

*

0

γ=

⎟

⎠

⎞

⎜

⎝

⎛

−

γ+β<β<

−

γ−β→

εε

∑

S

xxn

x

ktS

xxn

x

ktP

i

Отже, довірчий інтервал для параметра

*

0

β буде таким:

()

.,,

2

*

00

2

*

0 εε

∑

−

γ+β<β<

−

γ−β S

xxn

x

ktS

xxn

x

kt

i

(522)

2.5. Довірчий інтервал для парної лінійної функції регре-

сії із заданою надійністю

γ .

Ураховуючи те, що

*

0

β

і

*

1

β

є ви-

падковими величинами, то і лінійна функція регресії

()

xxy

i

−β+

*

1

буде випадковою. Позначимо через

*

i

y

значення

ознаки Y, обчислимо за формулою

(

)

xxyy

ii

−β+=

*

1

*

. (523)

Тоді

()

=β−+

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

−β+=−β+=

∑

*

1

2

*

1

*

1

*

Dxx

n

y

D

xx

n

y

DxxyDyD

i

ii

206

()

(

)

()

=

−

ε−

−+

⎟

⎠

⎞

⎜

⎝

⎛

ε+β+β

=

∑

2

10

xx

Dxx

n

x

D

i

ii

i

ii

()

(

)

(

)

()

(

)

(

)

()

=

−

σ−

+

ε

=

−

ε−

−+

ε

=

∑

∑∑

ε

2

22

2

)(

xx

n

D

xx

Dxx

xx

n

D

i

ii

i

ii

i

+

σ

=

ε

n

2

(

)

()

(

)

()

⎟

⎠

⎞

⎜

⎝

⎛

−

+σ=

−

σ−

∑∑

ε

2

1

xx

n

xx

i

.

Звідси дістали:

()

(

)

()

⎟

⎠

⎞

⎜

⎝

⎛

−

+σ=

∑

ε 2

2

2*

1

xx

n

yD

i

(524)

або

()

(

)

()

⎟

⎠

⎞

⎜

⎝

⎛

−

+=

∑

ε 2

2

2*

1

xx

n

SyD

i

. (525)

Випадкова величина

()

∑

−

+

−

=

ε

2

*

1

xx

n

S

yy

t

i

ii

(526)

має t-розподіл із

2

−

= nk

ступенями свободи. Ураховуючи (526),

можна побудувати довірчий інтервал для лінійної парної функції

регресії із заданою надійністю γ, а саме:

()

γ=

⎟

⎠

⎞

⎜

⎝

⎛

γ<

−

+

−

∑

ε

kt

xx

n

S

yy

P

i

ii

,

1

2

*

. (527)

З (527) випливає

()

(

)

()

<β+β<

−

+γ−β+β

∑

ε i

i

x

xx

n

Sktx

10

2

*

1

*

0

1

,

()

(

)

()

.

1

,

2

*

1

*

0

∑

−

+γ−β+β<

ε

xx

n

Sktx

i

(528)

Жлуктенко В. І., Наконечний С. І., Савіна С.С. Теорія ймовірностей і математична статистика: У 2-х ч. - Ч. ІІ. Математична статистика

Подождите немного. Документ загружается.