Жлуктенко В. І., Наконечний С. І., Савіна С.С. Теорія ймовірностей і математична статистика: У 2-х ч. - Ч. ІІ. Математична статистика
Подождите немного. Документ загружается.


МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ ЕКОНОМІЧНИЙ УНІВЕРСИТЕТ
Частина ІІ
Навчально-методичний посібник
У двох частинах
Рекомендовано Міністерством освіти і науки України
Київ 2001
ББК 22.17
Розповсюджувати та тиражувати
Ж 76
без офіційного дозволу КНЕУ заборонено
Рецензенти:
О. П. Суслов, д-р екон. наук, проф.
(НДЕІ М-ва економіки України)
О. А. Корольов, д-р екон. наук, проф.
(Київ. нац. торг.-екон. ун-т)
Гриф надано Міністерством освіти і науки України
Лист № 14/18.2-183 від 27.02.01
Жлуктенко В. І., Наконечний С. І., Савіна С. С.
Ж 76 Теорія ймовірностей і математична статистика: Навч.-
метод. посібник: У 2-х ч. — Ч. ІІ. Математична статистика. —
К.: КНЕУ, 2001. — 336 с.
ISBN 966–574–265–5
У другій частині пропонованого навчального посібника розглянуто основи
математичної статистики як науки, що вивчає ймовірнісну природу статистич-
них оцінок параметрів генеральної сукупності, та закони їх розподілу. Ці закони
застосовуються з метою побудови довірчих інтервалів параметрів генеральних
сукупностей, а також для перевірки правильності параметричних і непараметрич-
них статистичних гіпотез обробкою результатів вибірки
. Докладно висвітлюють-
ся теоретичні основи дисперсійного та регресійного аналізу.
До кожної теми наведено розв’язування типових задач із поясненнями, а на-
прикінці кожної теми — перелік теоретичних питань та блок прикладів для тес-
тування в аудиторних і домашніх умовах.
Посібник розрахований на самостійне вивчення курсу «Математична статис-
тика» студентами економічних вузів
усіх форм навчання.
ББК 22.17
© В.І. Жлуктенко,
С. І. Наконечний,
С. С. Савіна, 2001
ISBN 966–574–265–5 © КНЕУ, 2001
Навчальне видання
ЖЛУКТЕНКО Володимир Іванович
НАКОНЕЧНИЙ Степан Ількович
САВІНА Світлана Станіславівна
ТЕОРІЯ ЙМОВІРНОСТЕЙ
І МАТЕМАТИЧНА СТАТИСТИКА
Навчальний посібник
У двох частинах
Частина ІІ
МАТЕМАТИЧНА СТАТИСТИКА
Редактор Н. Царик
Художник обкладинки Т. Зябліцева
Технічний редактор Т. Піхота
Коректор А. Бородавко
Верстка Т. Мальчевської
Підписано до друку 2.08.2001. Формат 60×84/16. Папір офсетний №1.
Гарнітура Тип Таймс. Друк офсетний. Умов. друк. арк. 23,25.
Умов. фарбовідб. 23,69. Обл.-вид. арк. 26,46. Наклад 8500 прим. Зам. № 20-2077
Видавництво КНЕУ
03680, м. Київ, проспект Перемоги, 54/1
Свідоцтво про реєстрацію №235 від 07.11.2000
Тел./факс: (044) 458-00-66; (044) 446-64-58
E-mail: publish@kneu.kiev.ua
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ ЕКОНОМІЧНИЙ УНІВЕРСИТЕТ
ТЕОРІЯ ЙМОВІРНОСТЕЙ
І МАТЕМАТИЧНА СТАТИСТИКА
Навчально-методичний посібник
У двох частинах
Частина ІІ
МАТЕМАТИЧНА СТАТИСТИКА
У другій частині пропонованого навчального посібника розглянуто основи
математичної статистики як науки, що вивчає ймовірнісну природу статистич-
них оцінок параметрів генеральної сукупності, та закони їх розподілу. Ці закони
застосовуються з метою побудови довірчих інтервалів параметрів генеральних
сукупностей, а також для перевірки правильності параметричних і непараметрич-
них статистичних гіпотез обробкою результатів
вибірки. Докладно висвітлюють-
ся теоретичні основи дисперсійного та регресійного аналізу.
До кожної теми наведено розв’язування типових задач із поясненнями, а на-
прикінці кожної теми — перелік теоретичних питань та блок прикладів для тес-
тування в аудиторних і домашніх умовах.
Посібник розрахований на самостійне вивчення курсу «Математична статис-
тика» студентами економічних вузів
усіх форм навчання.
3
ВСТУП
Основним змістом математичної статистики є
систематизація, обробка і використання статистич-
ної інформації для виявлення статистичних законо-
мірностей ознаки або ознак певної сукупності еле-
ментів.
Оскільки суцільна обробка всіх елементів сукуп-
ності практично неможлива, то, як правило, застосо-
вується вибірковий метод. Отже, розрізняють генера-
льну і вибіркову сукупності.
Множина Ω однотипних елементів
, яким прита-
манні певні кількісні ознаки (розміри, вага, маса то-
що), утворює генеральну сукупність. Кількість усіх
елементів генеральної сукупності називають її обся-
гом і позначають символом
Ν
, значення якого здебі-
льшого невідоме.
Кожна непорожня підмножина А множини Ω
(А ⊂ Ω) випадково вибраних елементів із генераль-
ної сукупності називається вибіркою. Кількість усіх
елементів вибірки називають її обсягом і познача-
ють символом n. Його значення відоме, причому
воно набагато менше за обсяг генеральної сукупнос-
ті (n << N).
Математична статистика
розв’язує дві категорії
задач:
1) статистичне оцінювання (точкове, інтервальне)
параметрів генеральної сукупності;
2) перевірка правдивості статистичних гіпотез про
значення параметрів генеральної сукупності або про
закон розподілу ознаки генеральної сукупності на пі-
дставі обробки результатів вибірки.

4
РОЗДІЛ V
СТАТИСТИЧНІ РОЗПОДІЛИ ВИБІРКИ.
СТАТИСТИЧНІ ОЦІНКИ ПАРАМЕТРІВ
ГЕНЕРАЛЬНОЇ СУКУПНОСТІ
ТЕМА 12. СТАТИСТИЧНІ РОЗПОДІЛИ ВИБІРОК
ТА ЇХ ЧИСЛОВІ ХАРАКТЕРИСТИКИ
1. Загальна інформація
Кількісні ознаки елементів генеральної сукупності можуть бути
одновимірними і багатовимірними, дискретними і неперервними.
Коли реалізується вибірка, кількісна ознака, наприклад Х, набуває
конкретних числових значень (Х = х
і
), які називають варіантою.
Зростаючий числовий ряд варіант називають варіаційним.
Кожна варіанта вибірки може бути спостереженою n
i
раз
(n
i
≥ 1 ), число n
i
називають частотою варіанти x
i
.
При цьому
∑
=
=
k
i
i
nn
1
, (350)
де k — кількість варіант, що різняться числовим значенням;
n — обсяг вибірки.
Відношення частоти n
i
варіанти x
i
до обсягу вибірки n назива-
ють її відносною частотою і позначають через W
i
, тобто
n
n
W
i
i
=
. (351)
Для кожної вибірки виконується рівність
∑
=
=
k
i
i
W
1
1
. (352)
Якщо досліджується ознака генеральної сукупності Х, яка є
неперервною, то варіант буде багато. У цьому разі варіаційний
ряд — це певна кількість рівних або нерівних частинних інтерва-
лів чи груп варіант зі своїми частотами.

5
Такі частинні інтервали варіант, які розміщені у зростаючій
послідовності, утворюють інтервальний варіаційний ряд.
На практиці для зручності, як правило, розглядають інтерва-
льні варіаційні ряди, у котрих інтервали є рівними між собою.
2. Дискретний статистичний розподіл вибірки
та її числові характеристики
Перелік варіант варіаційного ряду і відповідних їм частот, або
відносних частот, називають дискретним статистичним розпо-
ділом вибірки.
У табличній формі він має такий вигляд:
X = x
i
x
1
x
2
x
3
… x
k
n
i
n
1
n
2
n
3
… n
k
W
i
W
1
W
2
W
3
… W
k
Дискретний статистичний розподіл вибірки можна подати ем-
піричною функцією F
∗
(x).
Емпірична функція F
∗
(x) та її властивості. Функція аргумен-
ту х, що визначає відносну частоту події X < x, тобто
n
n
xXWxF
x
=<=
∗
)()(
, (353)
називається емпіричною, або комулятою.
Тут n — обсяг вибірки;
n
x
— кількість варіант статистичного розподілу вибірки, зна-
чення яких менше за фіксовану варіанту х;
F
∗
(x) — називають ще функцією нагромадження відносних
частот.
Властивості F
∗
(x):
1) 0 ≤ F
∗
(x) ≤ 1;
2) F(x
min
) = 0, де x
min
є найменшою варіантою варіаційного ряду;
3)
1)(
max
=
>xx
xF
, де x
max
є найбільшою варіантою варіаційного
ряду;
4) F(x) є неспадною функцією аргументу х, а саме: F(x
2
) ≥ F(x
1
)
при x
2
≥
x
1
.
Полігон частот і відносних частот. Дискретний статистич-
ний розподіл вибірки можна зобразити графічно у вигляді лама-
ної лінії, відрізки якої сполучають координати точок (x
i
; n
i
), або
(x
i
; W
i
).
6
У першому випадку ламану лінію називають полігоном час-
тот, у другому — полігоном відносних частот.
Приклад. За заданим дискретним статистичним розподі-
лом вибірки
X = x
i
–6 –4 –2 2 4 6
n
i
5 10 15 20 40 10
W
i
0,05 0,1 0,15 0,2 0,4 0,1
потрібно:
1. Побудувати F
∗
(x) і зобразити її графічно;
2. Накреслити полігони частот і відносних частот.
Розв’язання. Згідно з означенням та властивостями F
∗
(x) має такий
вигляд:
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎨
⎧
>
≤<
≤<
≤<−
−≤<−
−≤<−
−
≤
==<=
∗
.6,1
,649,0
,425,0
,223,0
,2415,0
,4605,0
,60
)()(
x
x
x
x
x
x
x
n
n
xXWxF
x
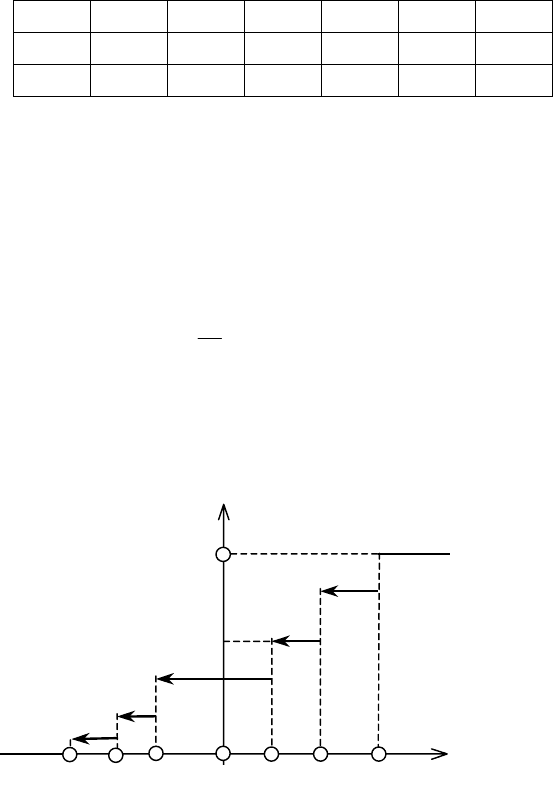
Графічне зображення F
∗
(x) подано на рис. 106.
–
6 –4 –2 0 2 4 6
х
і
1
(
)
xF
*
Рис. 106
Полігони частот та відносних частот зображено на рис.107, 108.
