Живоглядов В.Г. Теория движения транспортных и пешеходных потоков
Подождите немного. Документ загружается.

по эмпирической формуле y=252 000 000*x
-1
Таким образом, размах отклонений значений табличных от вычисленных
0, среднее взвешенное отклонение составляет 0,00 %, что дает основание
подтвердить точность выбранной эмпирической кривой.
3. Изучение зависимости суммарной количества поездок населения на
МПТ от количества человек на одно ТС. Анализ проведен на основе данных
табл. 10.5 и рис. 10.2. Для правильного выбора вида аналитической зависи-
мости выполняются промежуточные вычисления. На отрезке изменения пе-
ременной x, т.е. х
[2; 18] выберем точки х
1
= 2 и х
n
= 18 наиболее удаленных
друг от друга (крайние). Вычисляется х
арм
, х
геом
, х
гарм
по формулам (2.265) и на
графике геометрически находятся соответствующие значения переменной у.
По данным табл. 10.5 находятся у
арм
, у
геом
, у
гарм
, при этом используются фор-
мулы (2.266).
x
арм
=
10
y
арм
=
23457778
y*
1
=
29232000
x
геом
=
6
y
геом
=
22319745
y*
2
=
27066667
x
гарм
=
3,6
y
гарм
=
21236923
y*
3
=
22736000
Сравнивая числовые значения у*
1
, у*
2
, у*
3
с у
арм
, у
геом
, у
гарм
и оценивая
погрешности проведенных вычислений по формулам (2.267)-(2.273) получе-
ны следующие результаты:
ε
1
=|
y*
1
-y
арм
|=
5774222
ε
5
=|
y*
2
-y
геом
|=
4746922
ε
2
=|
y*
1
-y
геом
|=
6912255
ε
6
=|
y*
3
-y
арм
|=
721777,8
ε
3
=|
y*
1
-y
гарм
|=
7995077
ε
7
=|
y*
3
-y
гарм
|=
1499077
ε
4
=|
y*
2
-y
арм
|=
3608889
После этого выбирается минимальная погрешность ε из ε
i
, (i=1, 2,…7):
ε= min (ε
1
, ε
2
, ε
3
, ε
4
, ε
5
, ε
6
, ε
7
)= 721777,8
Так как ε совпадает с ε
6
, то в качестве аналитической зависимости хо-
рошим приближением служит зависимость у=а+b/х, с неизвестными пара-
метрами а и b. Для уточнения этих параметров используется МНК. Согласно
этому методу значения параметров функциональной зависимости а и b сле-
дует выбрать так, чтобы сумма квадратов погрешностей была наименьшей
921
(уравнение (2.274)), т.е. F(а, в) =
n
i
ii
baxfy
1
2
)),;((( будет минимальной, где ε
i
= у
i
– f (x
i
; a, b) – i – я погрешность (i=1, 2,…7). Необходимым условием су-
ществования минимума функции двух переменных является равенство нулю
всех ее частных производных. Значения параметров а и b найдем из системы
уравнений (2.275). Поскольку зависимость получилась нелинейная, то следу-
ет применять преобразование координат к функции у=а+b/х. Преобразовав
у=а+b/х, получим: у=а+b/х, т.е. Z = A
1
t + B
1
, где Z =у; A
1
= b; B
1
= a; t = 1/x.
Система уравнений (2.275) примет следующий вид (случай линейной
зависимости):
n
i
i
n
i
i
n
i
ii
n
i
i
n
i
i
znBtA
tztBtA
1
1
1
2
1
11
1
1
2
1
или
n
i
i
n
i
i
n
i
x
i
n
i
i
n
i
i
ynaxb
y
y
xaxb
11
111
2
/1)/1(
Далее, находятся значения а и b, путем решения системы матричным
методом, предварительно осуществив расчеты, которые приведены в
табл.10.10.
Таблица 10.10
Данные расчетов для МНК при исследовании зависимости суммарного коли-
чества поездок населения на МПТ от количества человек
на одно транспортное средство
i x
i
y
i
1/x
i
(1/x
i
)
2
x
i
y
i
1 2 16240000 0,5 0,25 8120000
2 4 24360000 0,25 0,0625 6090000
3 6 27066667 0,166666667 0,027778 4511111,1
4 8 28420000 0,125 0,015625 3552500
5 10 29232000 0,1 0,01 2923200
6 12 29773333 0,083333333 0,006944 2481111,1
7 14 30160000 0,071428571 0,005102 2154285,7
8 16 30450000 0,0625 0,003906 1903125
9 18 30675556 0,055555556 0,003086 1704197,5
∑ 90 2,46*10+08 1,414484127 0,384942 33439530
Итак, дана матрица коэффициентов при неизвестных вида:
L=
0,384942
1,414484
1,414484
9
а также матрица свободных членов
922

M=
33439530
246377556
Используя X=L
-1
M, получим
Х=
-32480000
32480000
где a= 32480000, b= -32480000, отсюда эмпирическая зависимость у=а+b/х
при найденных значениях a и b принимает вид
y=32 480 000+-32 480 000/x
Для определения точности выбора эмпирической кривой, т.е. макси-
мального отклонения табличных значений от аппроксимирующей кривой
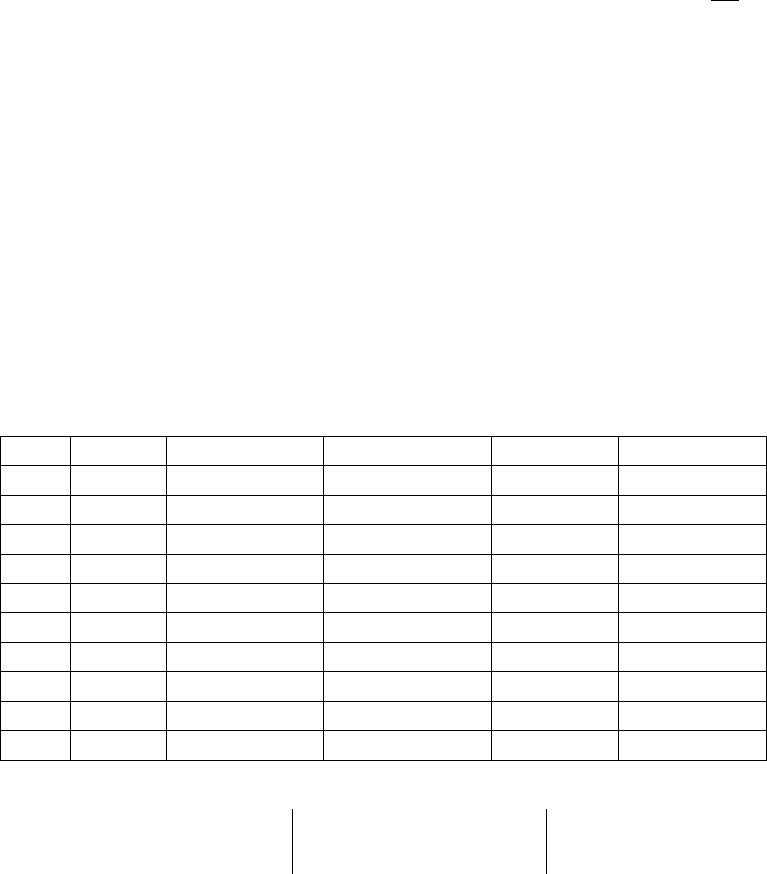
y=32 480 000+-32 480 000/x составим сравнительную табл. 10.11.
Таблица 10.11
Результаты отклонений табличных значений от значений, вычисленных по
эмпирической формуле y=32 480 000+-32 480 000/x
x
i
y
i
y
i
выч
γ
i
%
2
16240000
16240000
0
0,00
4
24360000
24360000
0
0,00
6
27066667
27066666,67
3,73*10
-
9
0,00
8
28420000
28420000
0
0,00
10
29232000
29232000
0
0,00
12
29773333
29773333,33
3,73*10
-
9
0,00
14
30160000
30160000
0
0,00
16
30450000
30450000
0
0,00
18
30675556
30675555,56
0
0,00
Результаты отклонений табличных значений от вычисленных по эмпи-
рической формуле представлены на рис. 10.6.
0
5000000
10000000
15000000
20000000
25000000
30000000
35000000
2 4 6 8 10 12 14 16 18
Yi,Yiвыч
Xi
Yi
Yiвыч
Рис. 10.6. Результаты отклонений табличных значений от значений, вычисленных
по эмпирической формуле y=32 480 000+-32 480 000/x
923
Таким образом, размах отклонений значений табличных от вычисленных
0, среднее взвешенное отклонение составляет 0,00 %, что дает основание
подтвердить точность выбранной эмпирической кривой.
4. Изучение зависимости суммарного количества поездок населения на
личном автотранспорте от количества человек на одно ТС. Анализ прове-
ден на основе данных табл. 10.5 и рис. 10.2. Для правильного выбора вида
аналитической зависимости выполняются промежуточные вычисления. На
отрезке изменения переменной x, т.е. х
[2; 18] выберем точки х
1
= 2 и х
n
= 18
наиболее удаленных друг от друга (крайние). Вычисляется х
арм
, х
геом
, х
гарм
по
формулам (2.265) и на графике геометрически находятся соответствующие
значения переменной у. По данным табл. 10.5 находятся у
арм
, у
геом
, у
гарм
, при
этом используются формулы (2.266).
x
арм
=
10
y
арм
=
14666667
y*
1
=
5280000
x
геом
=
6
y
геом
=
8800000
y*
2
=
8800000
x
гарм
=
3,6
y
гарм
=
5280000
y*
3
=
15
840000
Сравнивая числовые значения у*
1
, у*
2
, у*
3
с у
арм
, у
геом
, у
гарм
и оценивая
погрешности проведенных вычислений по формулам (2.266)-(2.272) получе-
ны следующие результаты:
ε
1
=|
y*
1
-y
арм
|=
9386667
ε
5
=|
y*
2
-y
геом
|=
0
ε
2
=|
y*
1
-y
геом
|=
3520000
ε
6
=|
y*
3
-y
арм
|=
1173333
ε
3
=|
y*
1
-y
гарм
|=
0
ε
7
=|
y*
3
-y
гарм
|=
10560000
ε
4
=|
y*
2
-y
арм
|=
5866667
После этого выбирается минимальная погрешность ε из εi, (i=1, 2,…7):
ε= min (ε
1
, ε
2
, ε
3
, ε
4
, ε
5
, ε
6
, ε
7
) = 0
Так как ε совпадает с ε
3
и ε
5
, то в качестве аналитической зависимости
хорошим приближением может служить зависимость у=1/(ах+b) или у=ах
b
, с
неизвестными параметрами а и b, для второй зависимости параметры а и b
оказываются более простыми числами, поэтому выберем в качестве искомой
зависимости у=ах
b
. Для уточнения этих параметров используется МНК. Со-
гласно этому методу значения параметров функциональной зависимости а и
924

b следует выбрать так, чтобы сумма квадратов погрешностей была наимень-
шей (уравнение (2.274)), т.е. F(а, в) =
n
i
ii
baxfy
1
2
)),;((( будет минимальной,
где ε
i
= у
i
– f (x
i
; a, b) – i-я погрешность (i=1, 2,…7).
Необходимым условием существования минимума функции двух пе-
ременных является равенство нулю всех ее частных производных. Значения
параметров а и b найдем из системы уравнений (2.275). Поскольку зависи-
мость получилась нелинейная, то следует применять преобразование коор-
динат к функции у = ах
в
. Прологарифмировав у = ах
в
, получим lg y = lg a +
b lg x, т.е. Z = A
1
+ B
1
t, где z = lg y; A
1
= lg a; B
1
= b; t = lg x.
Данная система (2.275) примет следующий вид (случай линейной зави-
симости):
n
i
i
n
i
i
n
i
ii
n
i
i
n
i
i
znAtB
tztAtB
1
1
1
2
1
11
1
1
2
1
или
n
i
i
n
i
i
n
i
ii
n
i
i
n
i
i
ynaxb
yxxaxb
11
111
2
lglglg
lglglglg)(lg
Далее, находятся значения а и b, путем решения системы матричным
методом, предварительно осуществив расчеты, которые приведены в
табл.10.12.
Таблица 10.12
Данные расчетов для МНК при исследовании зависимости суммарного количества
поездок населения на личном автотранспорте от количества человек на одно ТС
i
x
i
y
i
lg x
i
(lg x
i
)
2
lg y
i
lg x
i
lg y
i
1 2 26400000 0,301029996 0,090619 7,4216039 2,234125398
2 4 13200000 0,602059991 0,362476 7,1205739 4,287012679
3 6 8800000 0,77815125 0,605519 6,9444827 5,403857875
4 8 6600000 0,903089987 0,815572 6,8195439 6,158661844
5 10 5280000 1 1 6,7226339 6,722633923
6 12 4400000 1,079181246 1,164632 6,6434527 7,169489537
7 14 3771429 1,146128036 1,313609 6,5765059 7,537517774
8 16 3300000 1,204119983 1,449905 6,5185139 7,849072892
9 18 2933333 1,255272505 1,575709 6,4673614 8,118300968
∑
90 74684762 8,269032994 8,378042 61,234672 55,48067289
Итак, дана матрица коэффициентов при неизвестных вида:
L=
8,378042
8,269033
925

8,269033
9
а также матрица свободных членов
M=
55,480673
61,234672
Используя X=L
-1
M, получим
Х=
-1
7,722633923
где lg a= 7,722633923, b= -1, отсюда a=52800000.
Эмпирическая зависимость у=ах
b
при найденных значениях a и b при-
нимает вид: y=52800000*x
-1
Для определения точности выбора эмпирической кривой, т.е. макси-
мального отклонения табличных значений от аппроксимирующей кривой
y=52800000* x
-1
составим сравнительную табл. 10.13.
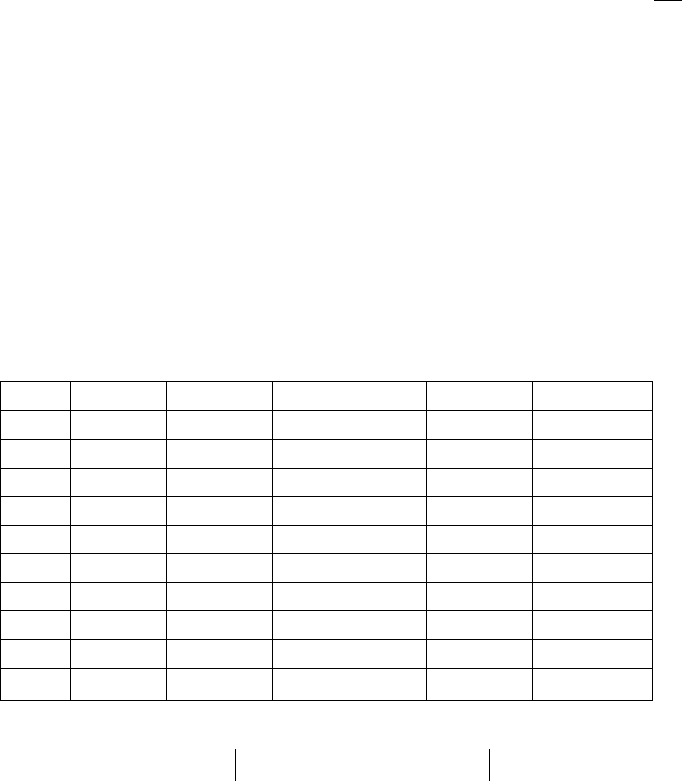
Таблица 10.13
Результаты отклонений табличных значений от значений, вычисленных по
эмпирической формуле y=52800000*x
-1
x
i
y
i
y
i
выч
γ
i
%
2
26400000
26400000
5,14*10
-
07
0,00
4
13200000
13200000
2,57*10
-
07
0,00
6
8800000
8800000
1,71*10
-
07
0,00
8
6600000
6600000
1,29*10
-
07
0,00
10
5280000
5280000
1,02*10
-
07
0,00
12
4400000
4400000
8,57*10
-
08
0,00
14
3771429
3771428,571
7,36*10
-
08
0,00
16
3300000
3300000
6,43*10
-
08
0,00
18
2933333
2933333,333
5,73*10
-
08
0,00
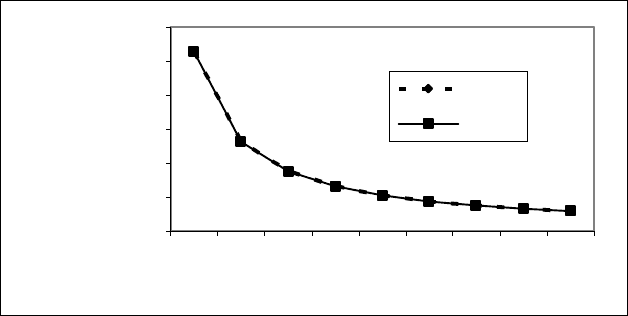
Результаты отклонений табличных значений от вычисленных по эмпи-
рической формуле представлены на рис. 10.7.
Таким образом, размах отклонений значений табличных от вычислен-
ных 0, среднее взвешенное отклонение составляет 0,00 %, что дает основание
подтвердить точность выбранной эмпирической кривой.
926
0
5000000
10000000
15000000
20000000
25000000
30000000
2 4 6 8 10 12 14 16 18
Xi
Yi,Yiвыч
Yi
Yiвыч
Рис. 10.5. Результаты отклонений табличных значений от значений, вычисленных
по эмпирической формуле y=52800000*x
-1
5. Изучение зависимости интенсивности движения МПТ на всех мар-
шрутах от количества человек на одно ТС. Анализ проведен на основе дан-
ных табл. 10.5 и рис. 10.3. Для правильного выбора вида аналитической зави-
симости выполняются промежуточные вычисления. На отрезке изменения
переменной x, т.е. х
[2; 18] выберем точки х
1
= 2 и х
n
= 18 наиболее удален-
ных друг от друга (крайние). Вычисляем х
арм
, х
геом
, х
гарм
по формулам (2.265) и
на графике геометрически находятся соответствующие значения переменной
у. По данным табл. 10.1 определяем у
арм
, у
геом
, у
гарм
, при этом используются
формулы (2.266).
x
арм
=
10
y
арм
=
1396,296
y*
1
=
1740
x
геом
=
6
y
геом
=
1328,556
y*
2
=
1611,111
x
гарм
=
3,6
y
гарм
=
1264,103
y*
3
=
1353,333
Сравнивая числовые значения у*
1
, у*
2
, у*
3
с у
арм
, у
геом
, у
гарм
и оценивая
погрешности проведенных вычислений по формулам (2.267)-(2.273) получе-
ны следующие результаты:
ε
1
=|
y*
1
-y
арм
|=
343,7037
ε
5
=|
y*
2
-y
геом
|=
282,5549
ε
2
=|
y*
1
-y
геом
|=
411,4437
ε
6
=|
y*
3
-y
арм
|=
42,96296
ε
3
=|
y*
1
-y
гарм
|=
475,8974
ε
7
=|
y*
3
-y
гарм
|=
89,23077
ε
4
=|
y*
2
-y
арм
|=
214,8148
После этого выбирается минимальная погрешность ε из εi, (i=1, 2,…7):
ε= min (ε
1
, ε
2
, ε
3
, ε
4
, ε
5
, ε
6
, ε
7
) = 42,96296
Так как ε совпадает с ε
6
, то в качестве аналитической зависимости хо-
рошим приближением служит зависимость у=а+b/х, с неизвестными пара-
927
метрами а и b. Для уточнения этих параметров используется МНК. Согласно
этому методу значения параметров функциональной зависимости а и b сле-
дует выбрать так, чтобы сумма квадратов погрешностей была наименьшей
(уравнение (2.274)), т.е. F(а, в) =
n
i
ii
baxfy
1
2
)),;((( будет минимальной, где ε
i
= у
i
– f (x
i
; a, b) – i-я погрешность (i=1, 2,…7).
Необходимым условием существования минимума функции двух пе-
ременных является равенство нулю всех ее частных производных. Значения
параметров а и b найдем из системы уравнений (2.275): Поскольку зависи-
мость получилась нелинейная, то следует применять преобразование коор-
динат к функции у=а+b/х. Преобразовав у=а+b/х, получим у=а+b/х, т.е. Z =
A
1
t + B
1
, где Z =у; A
1
= b; B
1
= a; t = 1/x.
Система уравнений (2.275) примет следующий вид (случай линейной
зависимости):
n
i
i
n
i
i
n
i
ii
n
i
i
n
i
i
znBtA
tztBtA
1
1
1
2
1
11
1
1
2
1
или
n
i
i
n
i
i
n
i
x
i
n
i
i
n
i
i
ynaxb
y
y
xaxb
11
111
2
/1)/1(
Далее, находятся значения а и b, путем решения системы матричным
методом, предварительно осуществив расчеты, которые приведены в
табл.10.14.
Таблица 10.14
Данные расчетов для МНК интенсивности движения МПТ на всех маршрутах
от количества человек на одно транспортное средство
i x
i
y
i
1/x
i
(1/x
i
)
2
x
i
y
i
1 2 966,6667
0,5 0,25 483,33333
2 4 1450 0,25 0,0625 362,5
3 6 1611,111
0,166666667 0,027778
268,51852
4 8 1691,667
0,125 0,015625
211,45833
5 10 1740 0,1 0,01 174
6 12 1772,222
0,083333333 0,006944
147,68519
7 14 1795,238
0,071428571 0,005102
128,23129
8 16 1812,5 0,0625 0,003906
113,28125
9
18 1825,926 0,055555556 0,003086 101,44033
∑
90 14665,33 1,414484127 0,384942 1990,4482
Итак, дана матрица коэффициентов при неизвестных вида:
L=
0,384942
1,414484
928
1,414484
9
а также матрица свободных членов
M=
1990,4482
14665,331
Используя X=L
-1
M, получим
Х=
-1933,333333
1933,333333
где a= 1933,333333, b= -1933,333333, отсюда
Эмпирическая зависимость у=а+b/х при найденных значениях a и b
принимает вид
y=1 933,3+-1 933,3/x.
Для определения точности выбора эмпирической кривой, т.е. макси-
мального отклонения табличных значений от аппроксимирующей кривой
y=1 933,3+-1 933,3/x составим сравнительную табл. 10.15
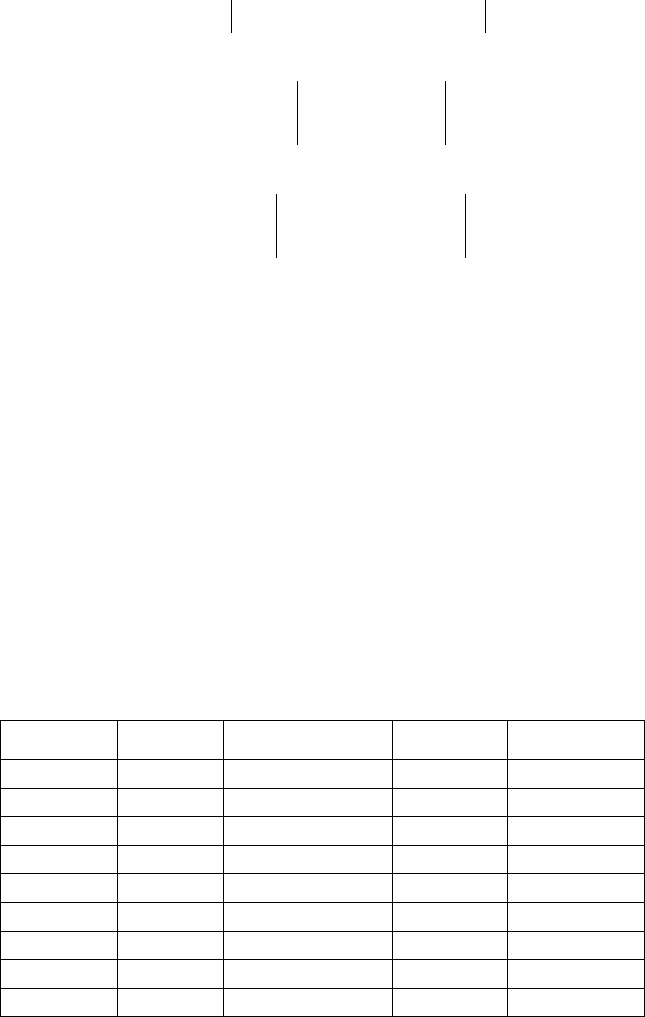
Таблица 10.15
Результаты отклонений табличных значений от значений, вычисленных по
эмпирической формуле y=1 933,3+-1 933,3/x
x
i
y
i
y
i
выч
γ
i
%
2 966,6667
966,6666667 1,02*10
-
12
0,00
4 1450 1450 2,27*10
-
13
0,00
6 1611,111
1611,111111 0 0,00
8 1691,667
1691,666667 2,27*10
-
13
0,00
10 1740 1740 2,27*10
-
13
0,00
12 1772,222
1772,222222 0 0,00
14 1795,238
1795,238095 0 0,00
16 1812,5 1812,5 2,27*10
-
13
0,00
18 1825,926
1825,925926 0 0,00
Результаты отклонений табличных значений от вычисленных по эмпи-
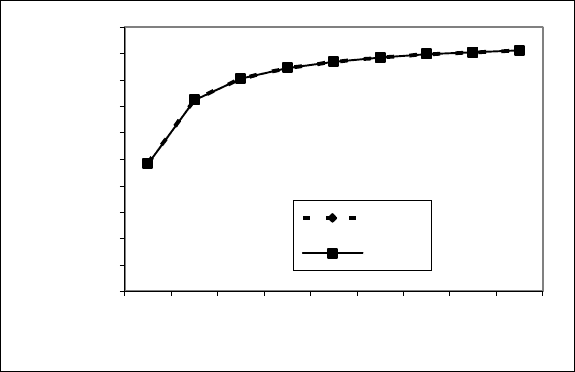
рической формуле представлены на рис. 10.8.
929
0
200
400
600
800
1000
1200
1400
1600
1800
2000
2 4 6 8 10 12 14 16 18
Xi
Yi,Yiвыч
Yi
Yiвыч
Рис. 10.8. Результаты отклонений табличных значений от значений, вычисленных
по эмпирической формуле y=1 933,3+-1 933,3/x
Таким образом, размах отклонений значений табличных от вычислен-
ных 0, среднее взвешенное отклонение составляет 0,00 %, что дает основание
подтвердить точность выбранной эмпирической кривой.
По нашему мнению, наличие и применение такой методологии позво-
лит более рациональнее формировать структуру дорожно – транспортных се-
тей и их атрибутики, а также с учетом этого топографию производственно –
промышленных, жилых зон, зон отдыха, торговли и т.п. К этому обязывает
еще и то, что производственный и социально – бытовой процессы находятся
в единстве с транспортным, поскольку последний является ускорителем не
только в них, но и в раскрытии творческих потенциалов личности, наконец.
Проведенное экспериментальное исследование посредством аппроксимиро-
ванного моделирования подтвердило правомерность теоретических разрабо-
ток и выводов.
930
