Живоглядов В.Г. Теория движения транспортных и пешеходных потоков

Подождите немного. Документ загружается.

483

= |4,5 – 53,564538| = 49,0645

= |4,5 – 2,722| = 1,7786

После этого выбираем минимальную погрешность ε из ε

, (i=1, 2,…7):

ε= min (ε

, ε

) = min {20,0345; 21,454; 30,808; 41,3345;

0,154; 49,0645; 1,7786} = 0,154

Так как ε

совпадает с ε

, то в качестве аналитической зависимости хо-

рошим приближением служит зависимость у = ах

, (в>0 – параболическая;

в<0 – гиперболическая), с неизвестными параметрами а и b. Для уточнения

этих параметров используется метод наименьших квадратов (МНК). Соглас-

но этого метода значения параметров функциональной зависимости а и в

следует выбрать так, чтобы сумма квадратов погрешностей была наимень-

шей (уравнение (2.273)), т.е. F(а, в) =







baxfy

)),;((( будет минимальной,

где ε

= у

– f (x

; a, b) – i-я погрешность (i=1, 2,…7).

Необходимым условием существования минимума функции двух пе-

ременных является равенство нулю всех ее частных производных. Значения

параметров а и в найдем из системы уравнений:















0),(

baF

или



























.0)),;(((

0)),;(((

fbaxfy

Поскольку зависимость получилась нелинейная, то следует применять

преобразование координат к функции у = ах

. Прологарифмировав у = ах

получим: lg y = lg a + b lg x, т.е. Z = A

+ B

t, где z = lg y; A

= lg a; B

= b;

t = lg x.

Данная система (2.275) примет следующий вид: (случай линейной за-

висимости):























znAtB

tztAtB

или

  

 























ynaxb

yxxaxb

111

lglglg

lglglglg)(lg

Далее находим значения b и lga путем решения системы по методу

561

484

Крамера, предварительно осуществив следующие расчеты, которые приведе-

ны в табл. 5.3.

Таблица 5.3

Данные расчетов суммарной интенсивности конфликтования при

отклонении (А) для МНК

i x

lg x

(lg x

)

lg y

(lg x

)(lg y

)

100

200

300

400

500

600

700

800

900

1,379

5,47

12,23

21,57

33,53

49,97

64,85

84,12

105,75

2,301029996

2,477121255

2,602059991

2,698970004

2,77815125

2,84509804

2,903089987

2,954242509

5,29473904

6,136129711

6,770716198

7,284439084

7,71812437

8,094582857

8,427931473

8,727548804

0,139564266

0,737987326

1,087426457

1,333850145

1,525433553

1,698709349

1,811909980

1,924899264

2,024280376

0,279128532

1,698130974

2,69368719

3,470758097

4,117099403

4,719271502

5,155061533

5,588155779

5,980215138

∑

4500

378,869

23,55976303

62,45421154

12,28406072

33,70150815

Результаты расчетов суммарной интенсивности конфликтования при

отклонении, сведенные в таблицу, осуществлены в среде Microsoft Excel.

После подстановки результатов, проведенных расчетов, помещенных в

табл. 5.3, система запишется в виде:

62,45421154*b + 23,55976303*lg a = 33,70150815

23,55976303*b + 9*lg a = 12,28406072

Для нахождения b и lga, вычисляется главный определитель ∆ системы,

т.е.

∆ = 62,45421154 23,55976303 = 9* 62,45421154 – (23,55976303)

23,55976303 9

= 562,0879116 – 555,062434 = 7,02547757 ≠ 0

Он не равен нулю, следовательно b и lga можно найти по формулам

Крамера, предварительно рассчитав ∆

и ∆

lg a

∆

lg a

= 62,45421154 33,70150815 = -26,80821902

23,55976303 12,28406072

∆

= 33,70150815 23,55976303 = 13,9040137

12,28406072 9







562

485

Значения lga и b имеют вид:

lga=

02547757,7

80821902,26





Lga

=-3,815857179,

отсюда а=10

-3,815857179

=0,000152807

b =

02547757,7

9040137,13





= 1,979084491

Эмпирическая зависимость у = ах

при найденных значениях a и b

принимает вид у =0,000152807 * х

1,979084491

Для определения точности выбора эмпирической кривой, т.е. макси-

мального отклонения табличных значений от аппроксимирующей кривой

у = 0,000152807 * х

1,979084491

составим сравнительную табл. 5.4.

Таблица 5.4

Результаты отклонений табличных значений от значений, вычисленных по

эмпирической формуле

выч

100

200

300

400

500

600

700

800

900

1,379

5,47

12,23

21,57

33,53

49,97

64,85

84,12

105,75

1,387753181

5,471117314

12,20606019

21,56948734

33,54539629

48,12151623

65,28789341

85,036155751

107,3590803

0,008753181

0,001117314

0,023979815

0,00051266

0,015396285

1,848483772

0,437893414

0,916155751

1,60908033

0,63

0,02

0,20

0,002

0,05

3,699

0,68

1,9

1,52

Результаты отклонений табличных значений от вычисленных по эмпи-

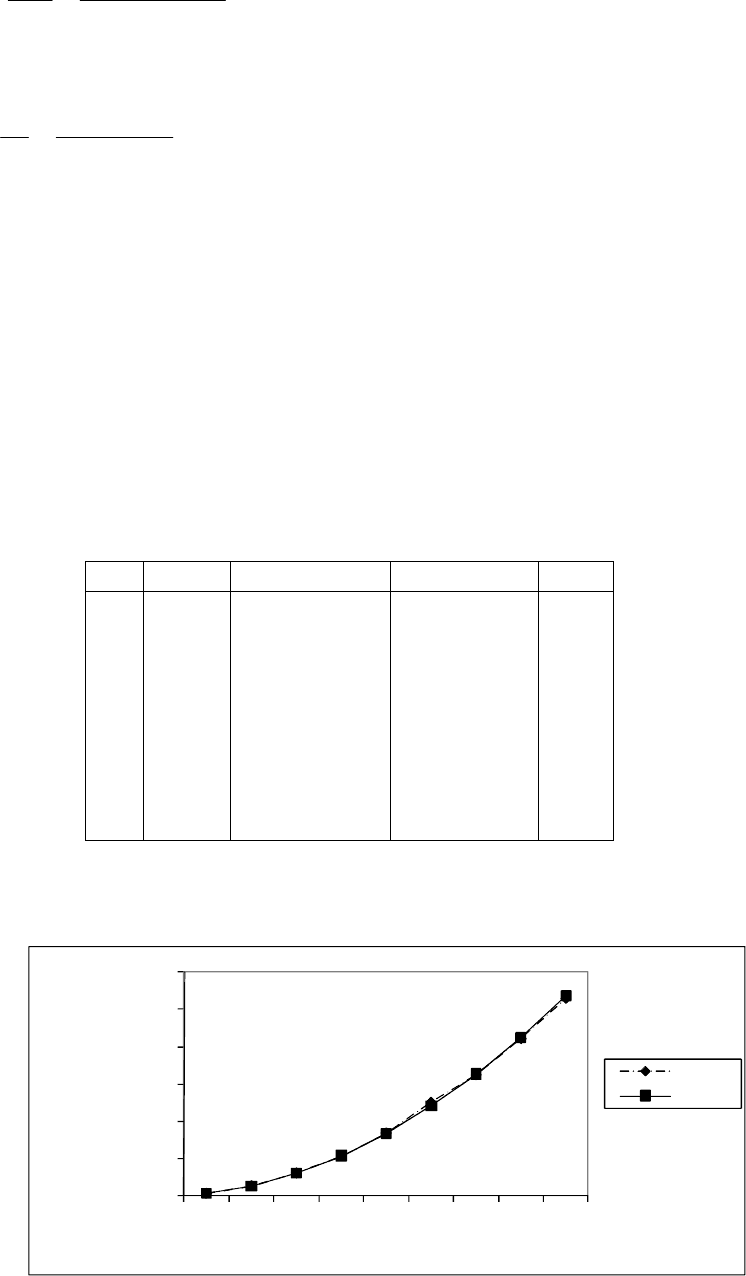
рической формуле представлены на рис. 5.44.

100

120

100 200 300 400 500 600 700 800 900

Интенсивность

конфликтования при

отклонении

Интенсивность движения, ТЕ/ч

y i

yi выч

Рис. 5.44. Результаты отклонений табличных значений от значений, вычис-

ленных по эмпирической формуле

563

486

Отклонение табличных значений от значений, вычисленных по эмпи-

рической формуле, взятых по абсолютной величине γ

, имеют вид:

= |y

– y

выч

где y

выч

– значения эмпирической функции в данных точках; y

– табличные

значения функции в заданных точках.

Таким образом, размах отклонений значений табличных от вычислен-

ных 0,00051  1,84848, среднее взвешенное отклонение составляет 0,002 

3,699 %, что дает основание подтвердить экспериментальные данные.

2. Изучение зависимости суммарной интенсивности конфликтования

при слиянии В от интенсивности движения. Результаты расчета приведены в

табл. 5.5.

Таблица 5.5

Результаты расчета суммарной интенсивности конфликтования при слиянии (В)

х 100 200 300 400 500 600 700 800 900

у 4,14

16,43

36,69

64,7

100,6

143,9

194,55

252,38

317,25

Для подбора вида аналитической зависимости у от х и уточнения пара-

метров этой зависимости используем предыдущую схему: эмпирическую за-

висимость выбираем из набора функций (3.1) - (3.7); строим точки:

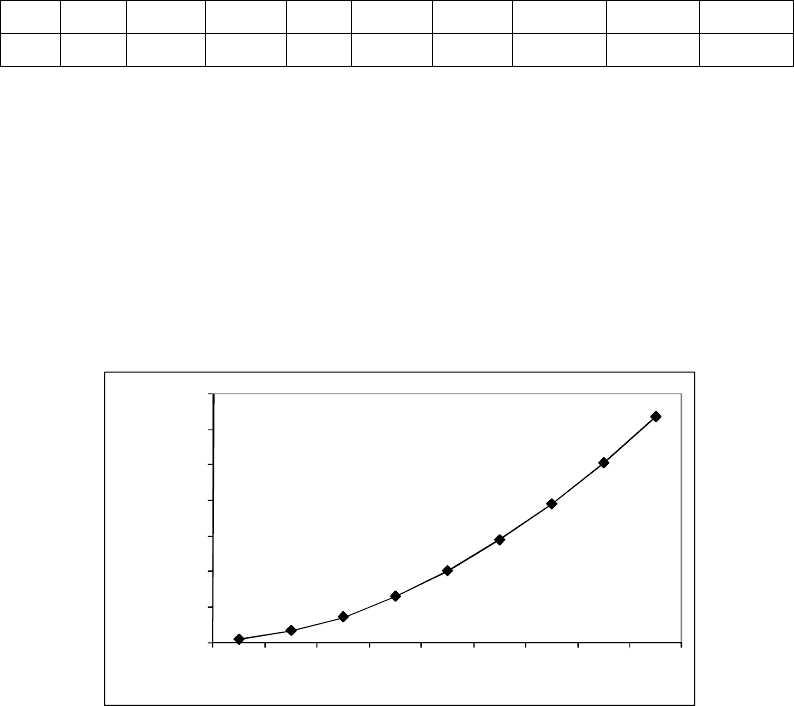
(100;4,14), (200;16,43), … , (900;317,25) и, соединив их плавно, получим гра-

фик функции (рис. 5.45), подобный одной из перечисленных выше семи

функций.

Рис. 5.45 Зависимость суммарной интенсивности конфликтования при слиянии (В) от

интенсивности движения

100

150

200

250

300

350

1 2 3 4 5 6 7 8 9

Интенсивность

конфликтования при слиянии

Интенсивность движения,ТЕ/ч

564

487

Далее выполним промежуточные вычисления. Выбирая крайние точки

на отрезке изменения переменной х, т.е. х

= 100; х

= 900 и вычисляя х

арм,

геом ,

гарм

по формуле (2.265) имеем:

арм

= (100 + 900) /2 = 500 ;

геом

= 900*100 = 300;

гарм

= 2*100*900/ (100 +900) = 180.

На графике найдем соответствующие значения переменной у: у*

; у*

;

у*

от средних значений х :

у*

= у (500 ) = 100,6; у*

= у (300 ) = 36,69; у*

= у (180 ) = 14.

По данным табл. 5.5 найдем у

арм

, у

геом

, у

гарм

, используя формулы

(2.265) и (2.266), где у

= 4,14 у

= 317,25.

арм

= (4,14 + 317,25) /2 =160,695;

геом

= 25,317*14,4 = 72,56776144;

гарм

= 2*4,14*317,25 / (4,14 +317,25) = 8,1733.

Сравнивая у*

; у*

с у

арм

, у

геом

, у

гарм

и оценивая погрешности ре-

зультатов сравнения по формулам (2.267)-(2.273) получаем:

= |100,6 – 160,695| =60,095 ;

= |100,6 – 36,2411| = 64,3589 ;

= |100,6 – 8,1733| = 92,4267;

= |36,69+ – 160,695| = 124,005 ;

= |36,69 – 36,2411| = 0.4489 ;

= |14 – 160,695| = 146,695 ;

= |14 – 8,1733| = 5,8267.

Находя минимальную погрешность ε

= min (ε

, ε

) =

= min {60,095; 64,3589; 92,4267; 124,005; 0,4489;146,695; 5,8267}=0,4489,

имеем при ε

= ε

аналитическую зависимость у = ах

, (b >0 – параболиче-

ская; b<0 – гиперболическая, с неизвестными параметрами а и в).

Для уточнения параметров а и в используется МНК, согласно которому

значения параметров а и в функциональной зависимости у = ах

выбираются

так, чтобы сумма квадратов погрешностей была наименьшей, т.е. F ( ba, ) =

565

488







baxfy

)),;((( будет минимальной (уравнение 2.274), где ε

= у

– f (x

;

a,b) – i-я погрешность.

Используя необходимое условие существования минимума функции

двух переменных, значения параметров а и в найдем из системы уравнений

(2.275). Поскольку зависимость получается нелинейная, то следует приме-

нять преобразование координат к функции у = ах

, т.е. lg y = lg (a x

) = lg a

+ lg (x

) = lg a + b lg x, где z = lg y; A = lg a; B = b; t = lg x, тогда в сис-

теме координат ZOt имеет линейную зависимость Z = A + Bt. Отсюда систе-

ма (2.275) будет подтверждена (2.275) (в случае линейной зависимости). Да-

лее, для нахождения значений

и lg a решаем систему по формуле Крамера,

предварительно осуществив следующие расчеты, сведенные в табл. 5.6.

Таблица 5.6

Расчетные данные по МНК для суммарной интенсивности конфликтования

при слиянии (В)

i x

lg x

(lg x

)

lg y

(lg x

)(lg y

)

100 4,14 2 4 0,617000341

1,234000682

200 16,43 2,301029996

5,294739041

1,215637563

2,797218497

300 35,69 2,477121255

6,136129711

1,552546548

3,845846053

400 64,7 2,602059991

6,770716198

1,810904281

4,712081577

500 100,6 2,698970004

7,284439084

2,002597981

5,404951881

600 143,9 2,77815125 7,71812437 2,158060794

5,995419293

700 194,55

2,84509804 8,094582857

2,289031235

6,512518281

800 252,38

2,903089987

8,427931473

2,402054936

6,973381633

900 317,25

2,954242509

8,727548805

2,501401631

7,389747031

4500

1129,6

23,55976303

62,45421154

16,54923531

44,86516493

Используя проведенные расчеты, получили систему:

62, 4542124*b + 23,55976303*lg a = 44,89489326

23,55976303*b + 9*lg a = 16,56123647,

которая имеет единственное решение при ∆ ≠ 0.

Для нахождения b и lga вычислим главный определитель системы:

∆ = 62,4542124 23,55976303 = 7,02547757 ≠ 0

23,55976303 9

566

489

Находим b и lga по формулам Крамера,

где

∆

lg a

= 62,4542124 44,89489326 = -23,3940805

23,55976303 16,56123647

∆

= 44,45421154 23,55976303 = 13,87523254

16,56123647 9

lga = = -3,022589953 или a = 10

– 3,022589953

= 0,000467852

b =

02547757,7

86175428,13





= 1,974987807

Эмпирическая зависимость примет вид: (b>0 – параболическая)

у = ах

= 0,000467852* х

1,974987807

;

Для определения точности выбора эмпирической кривой, т.е. макси-

мального отклонения точек таблицы от кривой у =0,000467852 * х

1,974987807

составим сравнительную табл. 5.7.

Таблица 5.7

Результаты отклонений табличных значений от значений, вычисленных по

эмпирической формуле

выч

100

200

300

400

500

600

700

800

900

4,14

16,43

35,69

64,7

100,6

143,9

194,55

252,38

317,25

4,1619

16,39135

36,5084

64,43847

100,1247

143,5236

194,5998

253,3237

319,6697

0,048827

0,062151

0,304680

0,455632

0,729706

0,649439

0,066380

1,558337

4,023826

0.707634

0,226995

0,498250

0,422468

0,435386

0,270768

0,020471

0,370468

0,761007

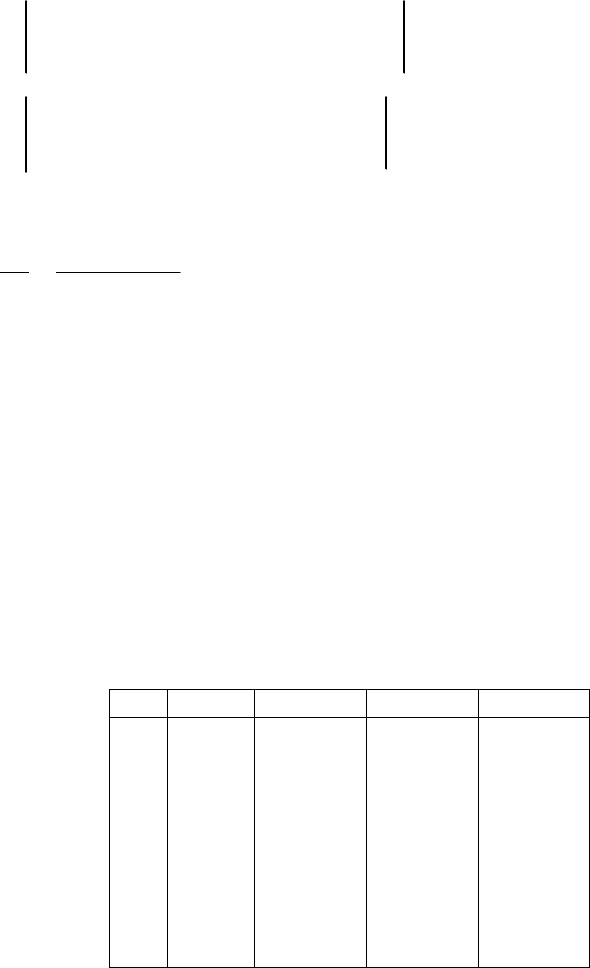
По таблице 5.7 построен график результатов отклонений табличных зна-

чений от значений, вычисленных по эмпирической формуле при слиянии (В).

567

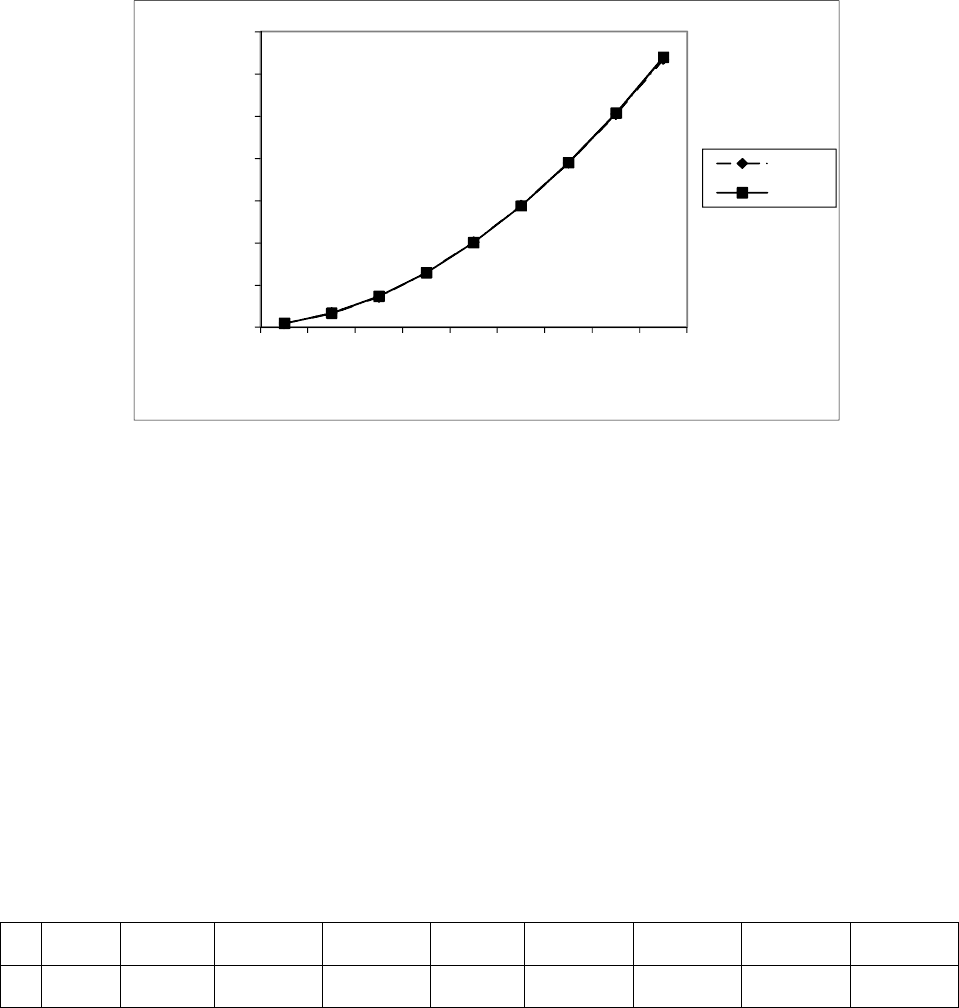
490

Таким образом, размах отклонений значений табличных от значений,

вычисленных при слиянии, составит 0,0204714,023826, а среднее взвешен-

ное отклонение составляет 0,020471  0,761007%, что дает основание под-

твердить экспериментальные данные.

3. Изучение зависимости суммарной интенсивности конфликтования

при пересечении С от интенсивности движения.

Таблица 5.7

Результаты расчета суммарной интенсивности конфликтования при пересечении (С)

х 100 200 300 400 500 600 700 800 900

у 6,90 27,38 61,615 107,85 167,6 239,85 324,26 420,64 528,75

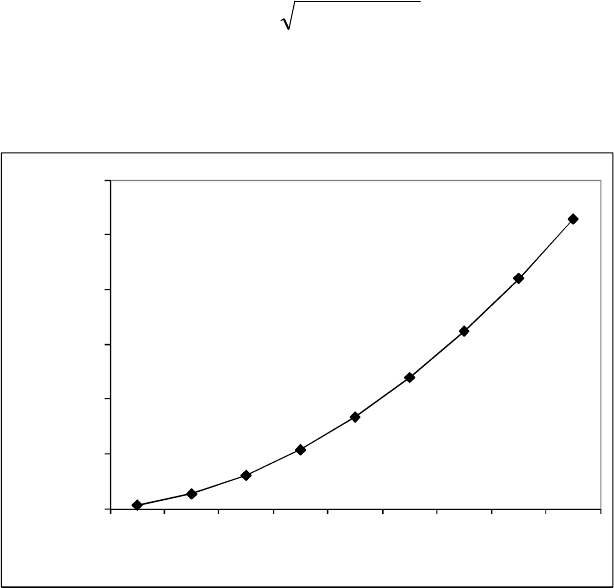
Выбор эмпирической зависимости осуществляем из набора функций

(2.258)-(2.264). Далее строим точки: (100;6,90), (200;27,38), … , (900;528,75)

и, соединив плавно, получим график функции (рис. 5.47), подобный одной из

(2.258) - (2.264) функций при крайних значениях х

= 100 и х

= 900. На

графике найдем соответствующие значения переменной у: у*

; у*

при

средних значениях х:

у*

= у (500) = 167,6; у*

= у (300) = 61,15; у*

= у (180) = 19.

По данным таблицы найдем у

арм

, у

геом

, у

гарм

, используя формулы:

арм

= (6,90 + 528,75) /2 =267,825;

100

150

200

250

300

350

1 2 3 4 5 6 7 8 9

Интенсивность

конфликтования при слиянии

Интенсивность движения, ТЕ/ч

y i

yi выч

Рис. 5.46. Результаты отклонений табличных значений от значений, вычис-

ленных по эмпирической формуле

568

491

геом

= 75,528*90,6 = 60,4018;

гарм

= 2*6,90*528,75 / (6,90 +528,75) =13,6222.

Сравнивая у*

; у*

с у

арм

, у

геом

, у

гарм

и оценивая погрешности ре-

зультатов сравнения, получим:

= |у*

– у

арм

| = |167,6 – 267,825| =100,225

= |у*

– у

геом

| = |167,6 – 60,4018| =107,1982

= |у*

– у

гарм

| = |167,6 – 13,6222| = 153,9778

= |у*

– у

арм

| = |61,15+ – 267,825| =206,675

= |у*

– у

геом

| = |61,15 – 60,4018| = 0.7482

= |у*

– у

арм

| =|19 – 267,825| = 248,825

= |у*

– у

гарм

| = |19 –13,6222| = 5,377

Находим минимальную погрешность ε

= min (ε

, ε

)

= min {100,225; 107,1982; 153,9778; 206,675; 0.7482; 248,825; 5,377} = 0,7482.

Так как ε

= ε

, то аналитическая зависимость будет у = ах

, (b>0 – па-

раболическая; b <0 – гиперболическая, с неизвестными параметрами а и b).

Для уточнения параметров а и b используем МНК, согласно которому значе-

ния параметров а и в функциональной зависимости у = ах

следует выбрать

так, чтобы сумма квадратов погрешностей была наименьшей, т.е. F(а, в) =

100

200

300

400

500

600

1 2 3 4 5 6 7 8 9

Интенсивность конфликтования при

пересечении

Интенсивность движения,ТЕ/ч

Рис. 5.47. Зависимость суммарной интенсивности конфликтования при пересечении (С)

от интенсивности движения

569

492







baxfy

)),;((( будет минимальной, где ε

= у

– f (x

, a,b) – i-я погреш-

ность.

Необходимым условием существования минимума функции двух пе-

ременных является равенство нулю всех ее частных производных.

Значения параметров а и b найдем из системы уравнений:















0),(

baF

или



























.0)),;(((

0)),;(((

fbaxfy

Поскольку зависимость получилась нелинейная, то следует применять

преобразование координат к функции у = ах

Прологарифмировав у = ах

, получим lg y = lg a + b lg x, т.е. Z = A

t, где z = lg y; A

= lg a; B

= b; t = lg x.

Данная система (3.18) примет следующий вид: (случай линейной зави-

симости):























znAtB

tztAtB

или

  

 























ynaxb

yxxaxb

111

lglglg

lglglglg)(lg

Предварительно осуществив следующие расчеты, найдем b и lga.

Таблица 5.9

Расчетные данные по МНК для суммарной интенсивности конфликтования

при пересечении (С)

i x

lg x

(lg x

)

lg y

(lg x

)(lg y

)

100

200

300

400

500

600

700

800

900

6,90

27,38

61,15

107,85

167,60

239,850

324,26

420,64

528,75

2,301029996

2,477121255

2,602059991

2,698970004

2,77815125

2,84509804

2,903089987

2,954242509

5,294739041

6,136129711

6,770716198

7,284439084

7,71812437

8,094582857

8,427931473

8,727548804

0,838849091

1,437433444

1,786396461

2,032820149

2,224274014

2,379939723

2,510893378

2,623910569

2,72325038

1,677698182

3,307577471

4,425120644

5,289519980

6,003248845

6,611832516

7,143737830

7,617448499

8,045142036

∑ 4500 1884,38 23,55976303 62,45421154 18,55776721 50,121326

После проведенных расчетов система запишется в виде:

570