Живоглядов В.Г. Теория движения транспортных и пешеходных потоков

Подождите немного. Документ загружается.

Так как ε

совпадает с ε

, то в качестве аналитической зависимости

хорошим приближением служит зависимость у=х/(ах+b) с неизвестными

параметрами а и b.

Для уточнения этих параметров используется МНК. Согласно этому

методу значения параметров функциональной зависимости а и b следует

выбрать так, чтобы сумма квадратов погрешностей была наименьшей

(уравнение (2.274)), т.е. F(а, b) =

(( ( ; , ))

i i

y f x a b







будет минималь-

ной, где ε

= у

– f (x

, a, b) – i-я погрешность (i=1, 2,…7).

Необходимым условием существования минимума функции двух пе-

ременных является равенство нулю всех ее частных производных.

Значения параметров а и b найдем из системы уравнений (2.275):















0),(

baF

или

(( ( ; , )) 0,

(( ( ; , )) 0.

i i a

i i b

y f x a b f







 









 







Поскольку зависимость получилась нелинейная, то следует приме-

нять преобразование координат к функции у=х/(ах+b). Преобразовав

у=х/(ах+b), получим: 1/у=(ах+b)/х=a+b/x, , т.е. Z = A

t + B

, где Z =1/у; A

b; B

= a; t = 1/x.

Система (2.275) примет следующий вид (случай линейной зависимо-

сти):

1 1

1 1 1

1 1

n n n

i i i i

i i i

n n

i i

A t B t z t

A t B n z

  

 



 







 





  

 

или

1 1 1

1 1

(1/ ) 1/ ,

1/ .

n n n

i i

i i i

i i

n n

i i

b x a x

x y

b x an

  

 



 







 





  

 

1071

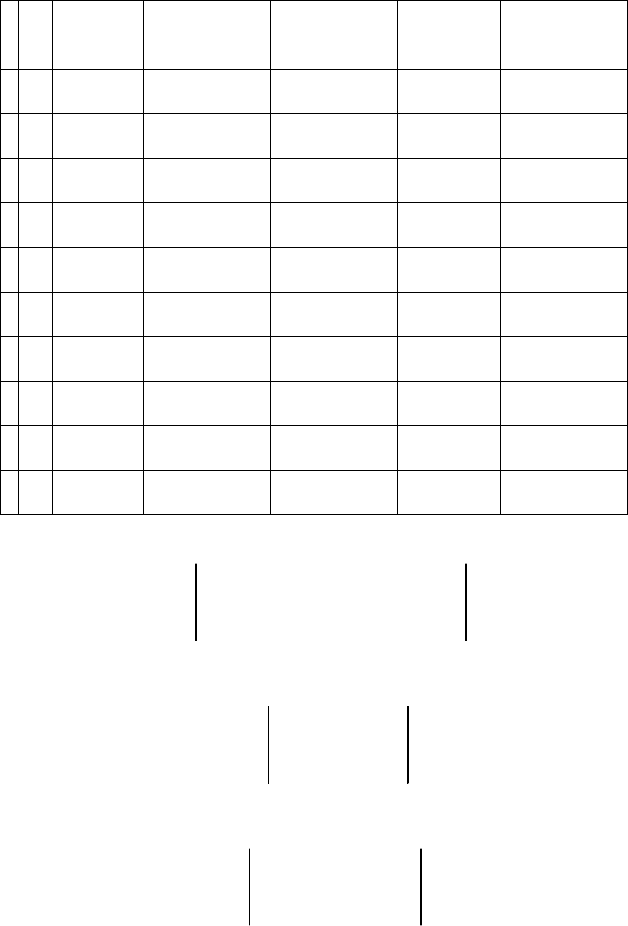
Далее находим значения а и b путем решения системы матричным

методом, предварительно осуществив расчеты, которые приведены в табл.

П 1.7.

Таблица П 1.7

Данные расчетов для МНК при определении зависимости

вероятности h от временного интервала t

1/y

1/ x

(1/x

)

1/y

0,2

0,019801

50,50166666

5 25 252,5083333

0,3

0,029554

33,8358333

3,33333333311,111111

112,786111

0,4

0,039211

25,50333324

2,5 6,25 63,75833311

0,5

0,048771

20,50416649

2 4 41,00833299

0,6

0,058235

17,17166637

1,6666666672,7777778

28,61944394

0,7

0,067606

14,79154714

1,4285714292,0408163

21,13078163

0,8

0,076884

13,00666596

1,25 1,5625 16,25833244

0,9

0,086069

11,6186101

1,1111111111,2345679

12,90956678

0,095163

10,50833194

1 1 10,50833194

∑

5,4

0,521294

197,4418212

19,2896825454,976773

559,4875671

Итак, дана матрица коэффициентов при неизвестных вида

54,97677 19,28968

19,28968 9

L 

а также матрица свободных членов

559,48757

197,44182

М 

Используя X = L

-1

M, получим

9,998427024

0,508370889

Х 

где a= 0,508370889, b= 9,998427024, отсюда эмпирическая зависимость

у=х/(ах+b) при найденных значениях a и b принимает вид

y=x/(0,5083709*x+9,9984270).

Для определения точности выбора эмпирической кривой, т.е. макси-

мального отклонения табличных значений от аппроксимирующей кривой

1072

y=x/(0,5083709*x+9,9984270) составим сравнительную табл. П 1.8.

Таблица П 1.8

Результаты отклонений табличных значений от значений,

вычисленных по эмпирической формуле y=x/(0,5083709*x+9,9984270)

выч

0,2 0,019801 0,019801782 0,0000005 0,00

0,3 0,029554 0,029553918 0,0000005 0,00

0,4 0,039211 0,039208862 0,0000017 0,00

0,5 0,048771 0,048768058 0,0000025 0,01

0,6 0,058235 0,058232924 0,0000025 0,00

0,7 0,067606 0,06760485 0,0000013 0,00

0,8 0,076884 0,076885198 0,0000015 0,00

0,9 0,086069 0,086075303 0,0000065 0,01

1 0,095163 0,095176476 0,0000139 0,01

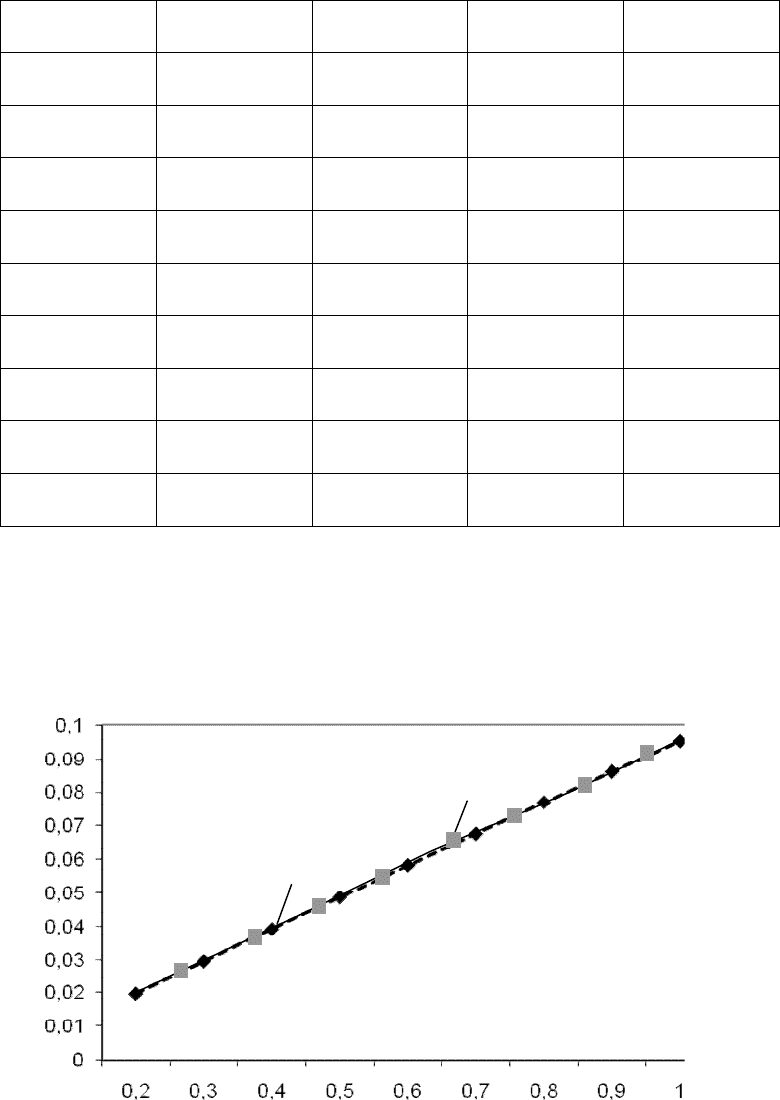
Результаты отклонений табличных значений от вычисленных по

эмпирической формуле y=x/(0,5083709*x+9,9984270) представлены на

рис. П 1.14.

Рис. П 1.14. Результаты отклонений табличных значений от значений,

вычисленных по эмпирической формуле y=x/(0,5083709*x+9,9984270)

, y

выч

1073

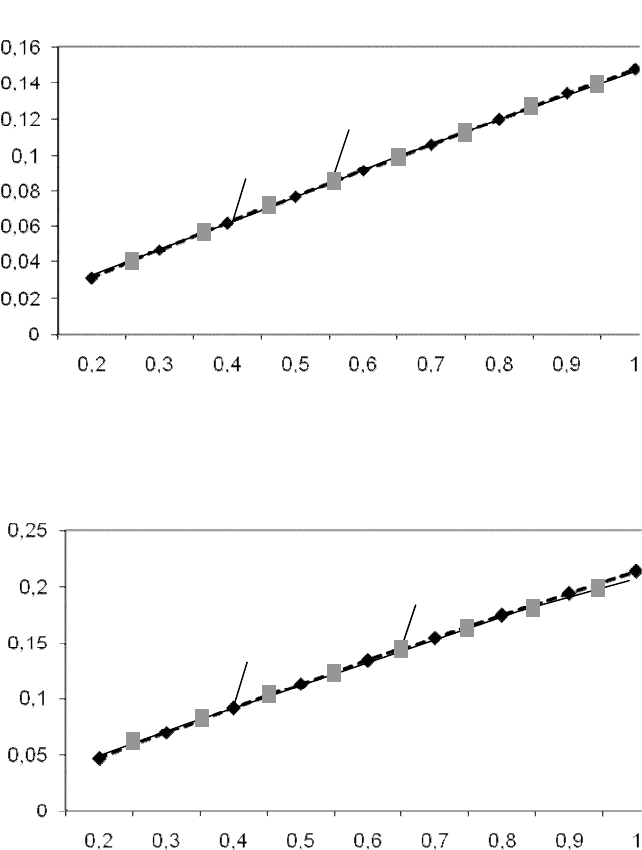
Рис. П 1.15. Результаты отклонений табличных значений от значений,

вычисленных по эмпирической формуле y=x/(0,5133908*x+6,2474839)

для интенсивности движения 0,16 ТЕ/с

Рис. П 1.16. Результаты отклонений табличных значений от значений,

вычисленных по эмпирической формуле y=x/(0,5200782*x+4,1628946) для интенсивно-

сти движения 0,24ТЕ/с

Таким образом, размах отклонений значений табличных от вычис-

ленных составляет 0,00000050,0000139, средневзвешенное отклонение –

0,00  0,01 %, что дает основание подтвердить точность выбранной эмпи-

рической кривой.

Для интенсивности движения 0,16 ТЕ/с зависимость вероятности от

временного интервала представлена уравнением y=x/(0,5133908*x+

+6,2474839), средневзвешенное отклонение составляет 0,00 0,04% (рис. П

1.15).

Для интенсивности движения 0,24 ТЕ/с зависимость вероятности от

временного интервала представлена уравнением y=x/(0,5200782*x

, y

выч

, y

выч

1074

+4,1628946), средневзвешенное отклонение составляет 0,01 0,08% (рис. П

1.16).

На основе данных таблиц и анализа графиков можно сделать сле-

дующие выводы:

1. Вероятность не появления ни одного ТС за очень малый про-

межуток времени (0,1 с) близка к единице при низкой интенсивности, с

ростом интенсивности движения вероятность появления несколько увели-

чивается (до 0,914). С увеличением промежутка времени вероятность дан-

ного события уменьшается тем быстрее, чем больше интенсивность при-

бытия ТС и достигает значения ноль даже для очень высокой интенсивно-

сти движения уже при интервале 40 с. Таким образом, максимум функции

вероятности не появления ни одного ТС при любой интенсивности прихо-

диться на интервал 0,1 с, все функции являются убывающими на всем вре-

менном интервале. Убывающий характер функции характерен только для

данного события.

2. Функции вероятности появления точно п числа ТС (исключая п=0)

имеют схожий характер. Для всех интенсивностей движения в начале вре-

менной шкалы функции распределения возрастают, достигают максимума

в некоторой точке t, зависящей от количества ТС и интенсивности движе-

ния, а далее убывают на всем протяжении временной шкалы и до + ∞.

3. С увеличением числа n вероятность выпадения данного события

уменьшается: если для n=0, P

≈1; n=1, Р

≈0,368, то при n=15, Р

≈0,102;

n=20, Р

≈0,088. Это объясняется увеличением количества возможных ва-

риантов, а следовательно, уменьшением вероятности выпадения одного из

них.

4. Максимальная вероятность появления данного п количества ТС

для различных интенсивностей движения практически одинакова, но вы-

падение максимума приходится на различные промежутки времени.

5. Максимум функции распределения вероятности тем сильнее сме-

щается вправо (наступает при большем промежутке времени), чем меньше

интенсивность движения и большее число n. Так, при появлении 1-ТС при

1075

интенсивности 0,9 ТЕ/с максимум вероятности достигает при t=0,1 с, а при

интенсивности 0,1 ТЕ/с максимум вероятности достигает при t=10с. Появ-

ление же 10 ТС характеризуется следующим распределением вероятности:

при интенсивности 0,9 ТЕ/с максимум вероятности достигает при t=6 с, а

при интенсивности 0,1 ТЕ/с максимум вероятности достигает при t=50 с.

6. Чем меньше интенсивность движения, тем более плавным являет-

ся график распределения вероятности: на большем промежутке времени он

возрастает, достигая максимума, и на большем убывает, достигая нулевого

значения, и наоборот.

7. Чем большее число n - количество прибывших ТС, тем более

плавным является график распределения вероятности: на большем проме-

жутке времени он возрастает, достигая максимума, и на большем убывает,

достигая нулевого значения, и наоборот. Это говорит о том, что более ве-

роятно прибытие большего количества ТС на большем интервале движе-

ния.

8. Чем большее число n - количество прибывших ТС, тем шире вре-

менной диапазон, в котором графики распределения вероятности достига-

ют своего максимума при различной интенсивности движения. Так, при n

=1 максимума функции распределения вероятности при всех интенсивно-

стях достигают в диапазоне от 0,1 до 10 с, при n =5 - в диапазоне от 10 до

50 с, при n =10 - в диапазоне от 10 до 100 с, а при n =15 максимума функ-

ция распределения вероятности при интенсивности 0,9 ТЕ/с достигает в

точке 20, а при интенсивности 0,1 ТЕ/с на изучаемом промежутке 0,1 ÷ 110

с функция распределения вероятности максимума не достигает. Это гово-

рит о том, что чем меньше интенсивность движения, тем больший проме-

жуток времени потребуется для прибытия большего количества ТС.

Итак, проведенное исследование подтвердило обоснованное приме-

нение закона распределения Пуассона в качестве математической модели

ТП в аспекте достоверности.

1076

Приложение 2

Применяемые на практике расчеты выбросов

отработанных газов

Расчетное значение массивного выброса:

1 1 1

k i r

p pn

пp

нn

i ij ij

j j j

М М М М

  

  

  

где k, l, r – соответственно число регулируемых пересечений, нерегули-

руемых пересечений и перегонов на данном участке. При этом имеется в

виду, что каждый отрезок УДС между двумя смежными перекрестками

при двухстороннем движении содержит два перегона, характеризую-

щихся различными параметрами движения для каждого из направлений;

нn

пp

М – соответственно массовые выброса данного токсич-

ного компонента на данном регулируемом пересечении, на нерегули-

руемых пересечениях и на перегоне, г/ч (г/сут).

Массовый выброс i-го токсичного компонента отработавших газов на

пересечении:

i ij

М m





где k – число транспортных регулируемых направлений на регулируе-

мом пересечении или число второстепенных направлений на нерегули-

руемых пересечениях;

– массовый выброс данного токсичного ком-

понента на j-м направлении, г/ч (г/сут).

Часовый массовый выброс i-го токсичного компонента отработавших

газов на данном пересечении:

2 2

1 1

3600

i j ij j ij

j j

m n N S N D

 

 

 

1077

где n

– доля ТС, остановившихся в данном направлении; N

– значение

часовой интенсивности движения для легковых (i=1) и грузовых авто-

мобилей (i=1) на данном направлении, авт/ч; S

(i=1,2:j=1,2) – усреднен-

ные значения массового выброса окислов углерода (i=1) и окислов азота

(i=2) для ТС j-й группы в расчете на одну остановку, г/ост (табл. П 2.1);

– средняя задержка; Р – значения массового выброса i-го токсичного

компонента для ТС j-й группы в расчете на один час работы двигателя

на холостом ходу, г/ч (табл. П 2.2)

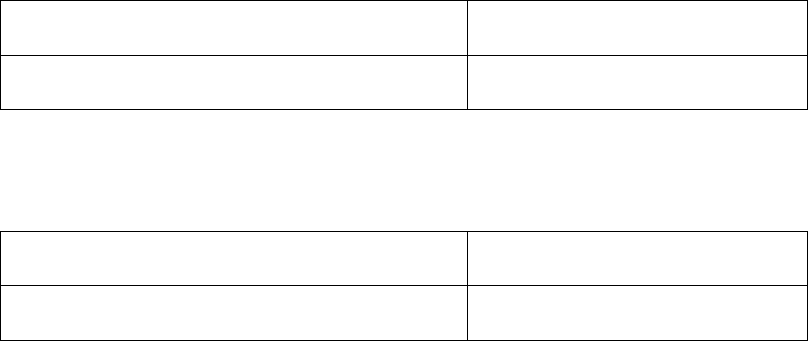
Таблица П 2.1

Усредненные значения массового выброса S токсичных компонентов

отработавших газов – окиси углерода и окислов азота в расчете

на одну остановку легковых автомобилей (числитель)

и грузовых автомобилей (знаменатель)

Окись углерода, г/ост 3,3/14,5

Окись азота, г/ост 0,42/2,2

Таблица П 2.2

Усредненные значения массового выброса Р токсичных

компонентов отработавших газов

Окись углерода, г/ч 286/697

Окись азота, г/ч 37/107

Суммарный массовый выброс токсичных компонентов на перегоне ма-

гистрали в граммах в час (г/ч):

пр

j ij i

М L N W K





где L – длина перегона, км; N

– часовая интенсивность легковых (i=1) и

грузовых (i=2) автомобилей; W

– коэффициент, соответствующий ус-

редненному значению массового выброса окислов углерода и окислов

азота в расчете на 1 км пробега для легковых и грузовых автомобилей,

г/(км авт) (табл. П 2.3); K

(i=1,2) – коэффициент, учитывающий влияние

скорости сообщения на усред-ненный массовый выброс токсичных ком-

1078

понентов – отработавших газов в расчете на 1 км пробега ТС j-й группы

(табл. П 2.4).

Таблица П 2.3

Значение коэффициента W

Окись углерода, г/км 21,0/51,4

Окись азота, г/км 2,7/7,9

Таблица П 2.4

Значение коэффициента K

Скорость сообщения, км/ч 10

для окиси углерода 1,8

1,63 1,5

1,35 1,2

для окислов азота 4,3

3,7

3,0

2,4

1,7

Стоимостная оценка потерь от загрязнения воздуха:

max

0,365

зв удi удi i

LN m

C D C



 



где L – длина магистрали, км; N

max

– интенсивность автомобилей опре-

деленного типа в час пик, авт/ч; m – коэффициент, учитывающий увели-

чение расхода топлива при движении с частыми остановками.

В общем виде при продолжительности остановки 20 с коэффициент уве-

личения расхода топлива

m = 142/L

ср

+1,

где L

ср

– среднее расстояние между остановками, м; K

– коэффициент

неравномерности движения; D

удi

– удельный выброс i-го вредного веще-

ства, Т; С

удi

– удельный ущерб от выброса i-го вещества, руб/1 тонну.

1079

ПРЕДИСЛОВИЕ

СПИСОК ОСНОВНЫХ ИСПОЛЬЗУЕМЫХ СОКРАЩЕНИЙ..

ВВЕДЕНИЕ

1. АНАЛИЗ СУЩЕСТВУЮЩИХ ТЕОРЕТИЧЕСКИХ ПРИ

Н-

ЦИПОВ И МЕТОДОВ РАСЧЕТА, ОЦЕНОК

ПРОПУСКА ТРАНСПОРТНЫХ И ПЕШЕХОДНЫХ

ПОТОКОВ. ЦЕЛИ И ЗАДАЧИ ИССЛЕДОВАНИЯ.

1.1

Анализ существующих ме

тодов расчета и оценки пропуска тран

с-

портных и пешеходных потоков на регулируемых перекрестках.

1.1.1

Анализ существующих принципов и методов расчета, оценок дл

и-

тельностей циклов, тактов, фаз светофорного регулирования дорож-

ного движения.

1.1.1.1

Зару

бежный опыт.

1.1.1.2

Отечественный опыт.

1.1.1.3

Условия применения светофорной сигнализации.

1.2

Анализ методов расчета пропускной способности регулируемого п

е-

рекрестка.

1.2.1

Потенциал перекрестка улиц и дорог.

1.3

Анализ методов расчета полной

очереди транспортных средств.

1.4

Анализ методов расчета времени рассасывания (временной длины)

очередей ТС, образовавшихся у стоп–линии за период действия за-

прещающих движение тактов СР.

1.5

Анализ существующих методов расчета и оценки задержек тран

с-

портных средств на регулируемых перекрестках.

1.6

1.6. Обобщение практики, анализ методов расчета и оценки об

разования и рассасывания заторовых состояний в дорожном движе-

нии.

1.6.1

Условия заторовых состояний.

1.6.2

Модель распространения заторов на

магистральных улицах.

1.7

Анализ существующих методов оценки пропускной способно

сти н

е-

1080