Zelditch M.L. (и др.) Geometric Morphometrics for Biologists: a primer

Подождите немного. Документ загружается.

chap-13 4/6/2004 17: 28 page 348

348 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

log (head length)

log (body length)

log (head depth)

log (body length)

Figure 13.16 A complex change in three parameters: early morphogenesis; modification of later

morphogenesis; and change in developmental rate and timing (due to increased body size). The

ancestor ontogeny is indicated by circles, the descendent ontogeny by squares.

Table 13.5 Allometric coefficients b and k and their standard errors for

S. gouldingi and S. manueli (see Figure 13.1 for the definition of the variables)

Variable S. gouldingi S. manueli

b (std error) k (std error) b (std error) k (std error)

v2 −0.94 (0.13) 0.81 (0.03) −1.81 (0.09) 1.03 (0.02)

v3 −0.61 (0.05) 0.89 (0.01) −0.47 (0.06) 0.87 (0.01)

v4 −1.16 (0.07) 0.85 (0.01) −1.27 (0.07) 0.90 (0.02)

v5 −2.64 (0.13) 1.23 (0.03) −1.45 (0.11) 0.96 (0.03)

v6 −1.40 (0.04) 1.04 (0.01) −1.14 (0.05) 1.00 (0.01)

v7 −1.51 (0.06) 1.00 (0.01) −1.80 (0.05) 1.09 (0.01)

v8 −1.38 (0.09) 0.93 (0.02) −1.00 (0.11) 0.85 (0.03)

v9 −1.97 (0.08) 1.10 (0.02) −1.81 (0.08) 1.06 (0.02)

v10 −1.76 (0.04) 1.22 (0.01) −1.56 (0.04) 1.17 (0.01)

v11 −1.93 (0.04) 1.20 (0.01) −1.59 (0.04) 1.13 (0.01)

v12 −1.60 (0.04) 1.14 (0.01) −1.32 (0.04) 1.08 (0.01)

v13 −2.38 (0.09) 1.19 (0.02) −2.27 (0.07) 1.15 (0.02)

v14 −2.23 (0.07) 1.12 (0.02) −2.10 (0.09) 1.08 (0.02)

v15 −1.68 (0.04) 1.21 (0.01) −1.41 (0.05) 1.15 (0.01)

v16 −1.78 (0.04) 1.23 (0.01) −1.52 (0.05) 1.17 (0.01)

v17 −1.55 (0.03) 1.17 (0.01) −1.24 (0.05) 1.10 (0.01)

v18 −2.57 (0.08) 1.17 (0.02) −1.98 (0.10) 1.05 (0.02)

v19 −1.94 (0.05) 1.09 (0.01) −1.62 (0.06) 1.02 (0.02)

v20 −1.69 (0.05) 1.10 (0.01) −1.40 (0.04) 1.04 (0.01)

v21 −1.99 (0.04) 1.23 (0.01) −1.74 (0.05) 1.17 (0.01)

v22 −1.83 (0.04) 1.22 (0.01) −1.56 (0.05) 1.16 (0.01)

v23 −1.47 (0.04) 1.07 (0.01) −1.30 (0.05) 1.03 (0.01)

v24 −1.67 (0.08) 0.94 (0.02) −2.70 (0.13) 1.13 (0.03)

v25 −2.69 (0.07) 1.12 (0.01) −2.57 (0.06) 1.09 (0.01)

v26 −1.56 (0.03) 1.13 (0.01) −1.37 (0.04) 1.09 (0.01)

v27 −1.82 (0.11) 0.90 (0.02) −3.41 (0.16) 1.23 (0.04)

v28 −1.23 (0.09) 0.81 (0.02) −1.89 (0.10) 0.97 (0.02)

v29 −1.16 (0.08) 0.75 (0.02) −1.50 (0.08) 0.82 (0.02)

v30 −0.64 (0.04) 0.90 (0.01) −0.51 (0.04) 0.89 (0.01)

chap-13 4/6/2004 17: 28 page 349

THE RELATIONSHIP BETWEEN ONTOGENY AND PHYLOGENY 349

(B)

(A)

1.12

.81

1.14

1.23

.75

.90

1.04

1.22

1.21

1.23

1.13

1.10

.89

1.00

1.23

1.00

.81

.85

.93

1.19

1.17

1.07

.90

.94

1.09

1.12

1.10

1.22

1.17

1.20

1.10

1.08

1.17

.8 2

1.13

.88

1.00

1.16

1. 16

1.18

1.09

1.04

1.09

.96

1.03

.97

.89

.87

.85

1.16

1.05

1.03

1.24

1.14

1.18

1.11

1.00

1.07

1.08

1.02

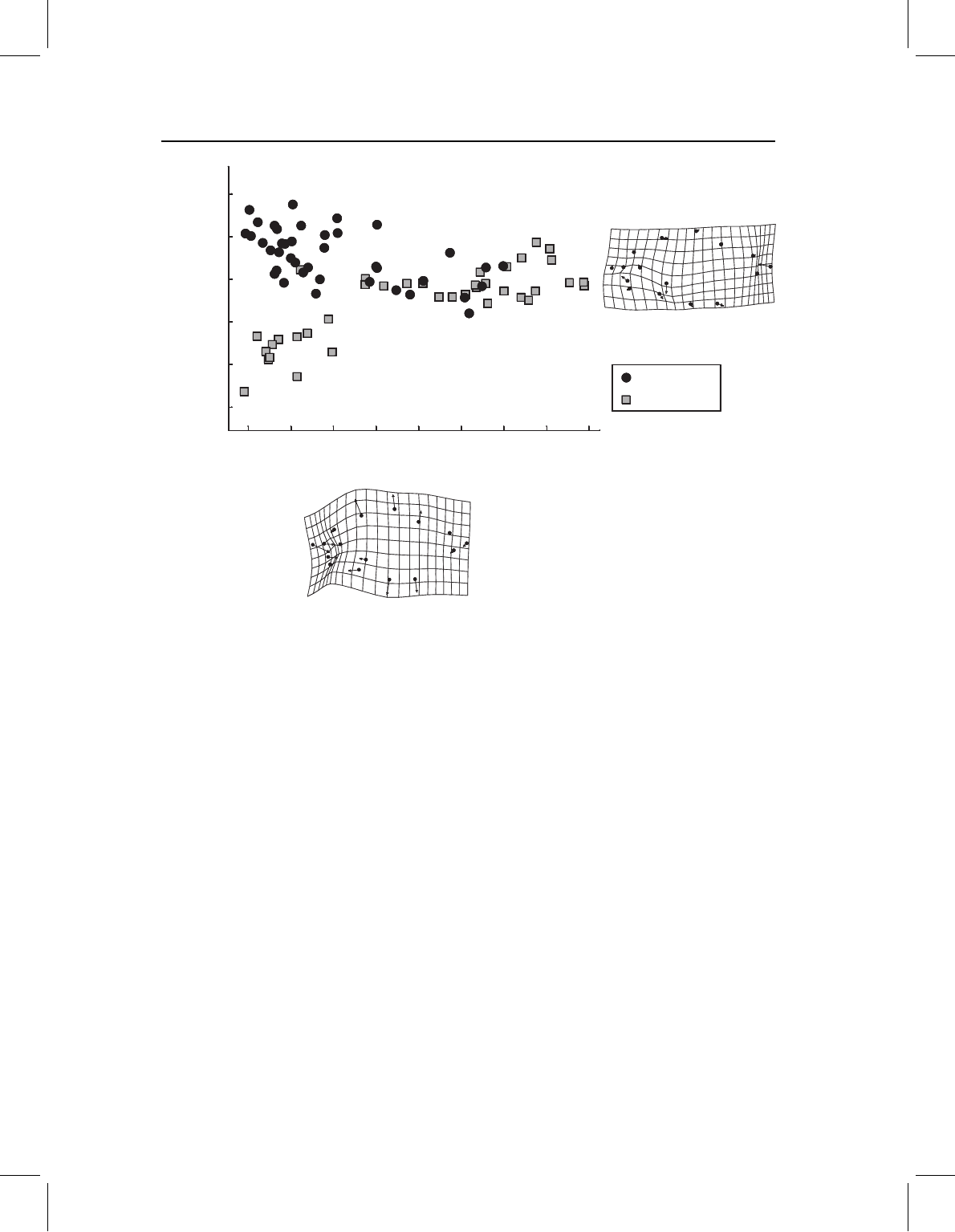
Figure 13.17 Allometric coefficients of S. gouldingi and S. manueli.

differ (Figure 13.17). Statistically, they differ in k for nearly all variables; the exceptions

are two in the head (v3 and v30), two anterior postcranial measurement (v9 and v13)

and the depth measurement of the caudal peduncle (v25). The angle between the vectors is

small (6.27

◦

), but is nonetheless significantly greater than 0.0

◦

(p < 0.05). Considering that

an angle of only just over 12.74

◦

indicates greater dissimilarity than expected by chance,

6.27

◦

does not seem so modest. There is some evidence, albeit slight, for an interaction

between modifications of early and late ontogeny that reduce disparity over ontogeny;

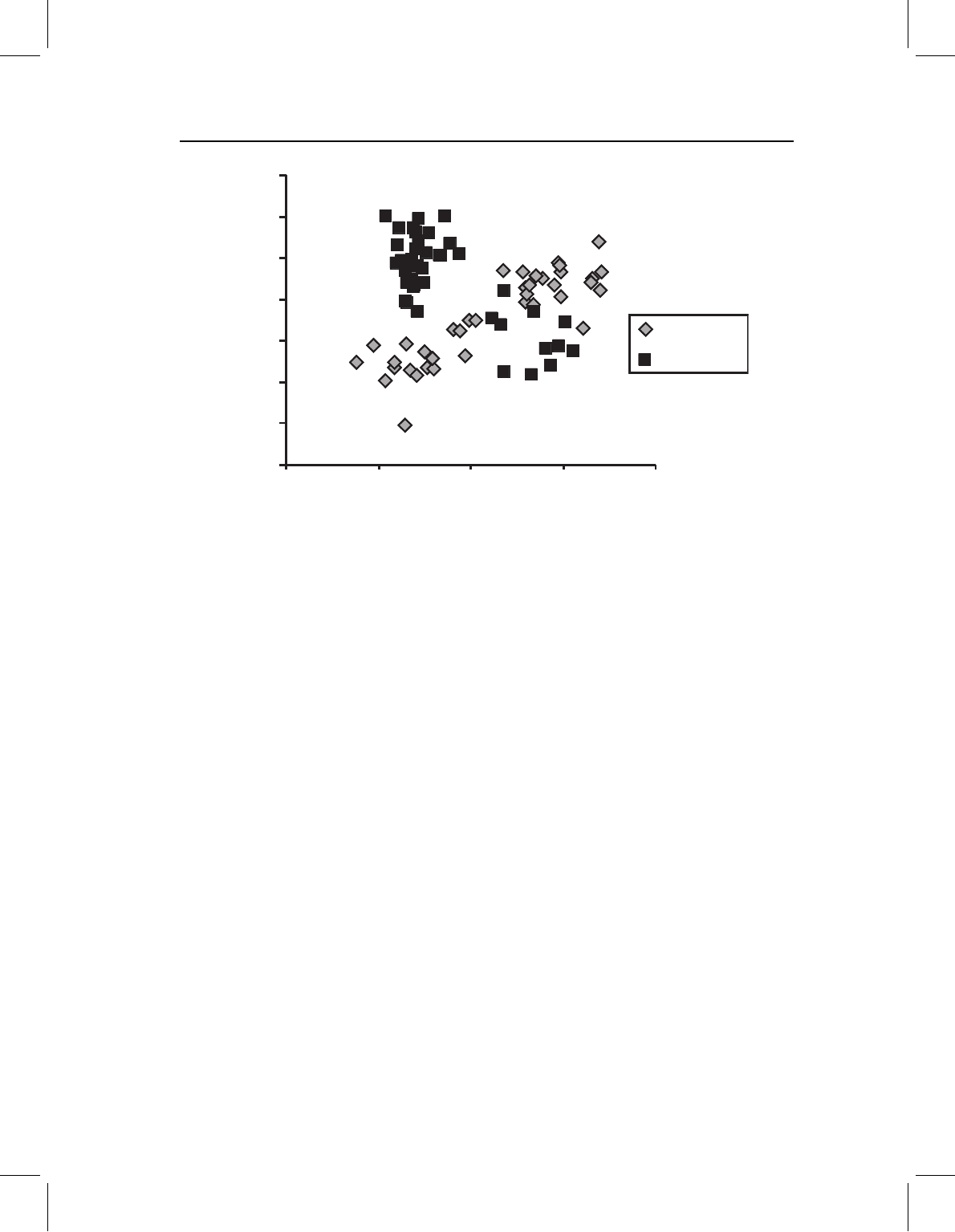
this pattern of counterbalancing modifications is suggested by the plot of PC2 on PC1

(Figure 13.18). Scores on PC1 increase with age, it also looks as though they are more

differentiated on PC2 earlier rather than later, and that they gradually reach a more similar

form. Yet the scale of PC2 is tremendously exaggerated in the plot; that axis accounts for

only 0.4% of the variance (PC1 accounts for 98.9%). So it is not clear whether this really

is a case of counterbalancing, an issue we will return to in the analysis of these species

using a geometric approach.

chap-13 4/6/2004 17: 28 page 350

350 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

⫺0.8

⫺0.6

⫺0.4

⫺10 0 5 10

PC1

0.6

0.4

0.2

⫺0.2

⫺5

PC2

S. gouldingi

S. manueli

Figure 13.18 PCA of the pooled ontogenetic data of S. gouldingi and S. manueli. The scale of

the Y-axis (PC2) is greatly exaggerated to make the separation between species more visible; older

specimens are to the right of the plot. The two species appear to differ, albeit subtly, in shape at the

outset of the measured stage and in their ontogenies. The modification of juvenile growth appears to

counterbalance the change in larval morphogenesis such that adults are more similar than juveniles.

Exploring evolutionary patterns of evolving ontogenies: geometric

morphometric analyses

Geometric studies of ontogenetic allometry are formally similar to traditional morphome-

tric ones, but there are important differences in the meanings of the parameters. Revisiting

the regression of geometric shape on size (covered in Chapter 10), the general bivariate

linear regression model is:

= mX

+ε

(13.4)

where Y is a shape variable, X is body size (measured by centroid size), b is the Y-intercept

and ε is the error term. Because we invariably analyze shape data multivariately, the model

we actually use is:

, Y

, ... Y

}={m

, m

, ...m

}X +{b

, b

, ...b

}+{ε

, ε

, ...ε

}

(13.5)

where {Y

, Y

...Y

} is the vector of shape variables (i.e. landmark coordinates

obtained by GLS, or partial warp scores including the uniform component), X is cen-

troid size, and {m

, m

, ...m

}, {b

, b

, ...b

} and {ε

, ε

, ...ε

} are vectors

of slope coefficients, intercepts and residuals, respectively.

One consequence of analyzing allometry using geometric data instead of traditional data

is that the allometric coefficients are no longer meaningful in terms of a specific growth

chap-13 4/6/2004 17: 28 page 351

THE RELATIONSHIP BETWEEN ONTOGENY AND PHYLOGENY 351

model – either a power law (Equation 13.1) or a sigmoidal curve of size or shape relative

to time. Instead, they indicate that shape changes with size. The underlying causes of those

changes are the same ones that account for allometric coefficients of traditional measure-

ments, but we cannot treat the coefficients as if they were rates of growth of individually

meaningful variables, nor can we use them to estimate time-lags between growth curves of

organs. Unlike the allometric coefficients of traditional measurements, those of geometric

shape variables have no individual biological meaning. For that reason, comparisons of

ontogenetic allometries using geometric variables are rarely (if ever) done bivariately. We

would not plot one shape variable at a time on size, except to check for linearity. In a geo-

metric analysis we are not comparing coefficients measurement-by-measurement; rather,

we are comparing whole sets of coefficients describing the ontogeny of an entire landmark

configuration. However, the difference in the meanings of the coefficients does not impede

our ability to recognize the patterns discussed above in the context of traditional measure-

ments. None of these patterns were defined in terms of particular coefficients; hence they

are not functions of a particular measurement scheme. We can thus examine the evidence

for them in geometric as well as traditional data.

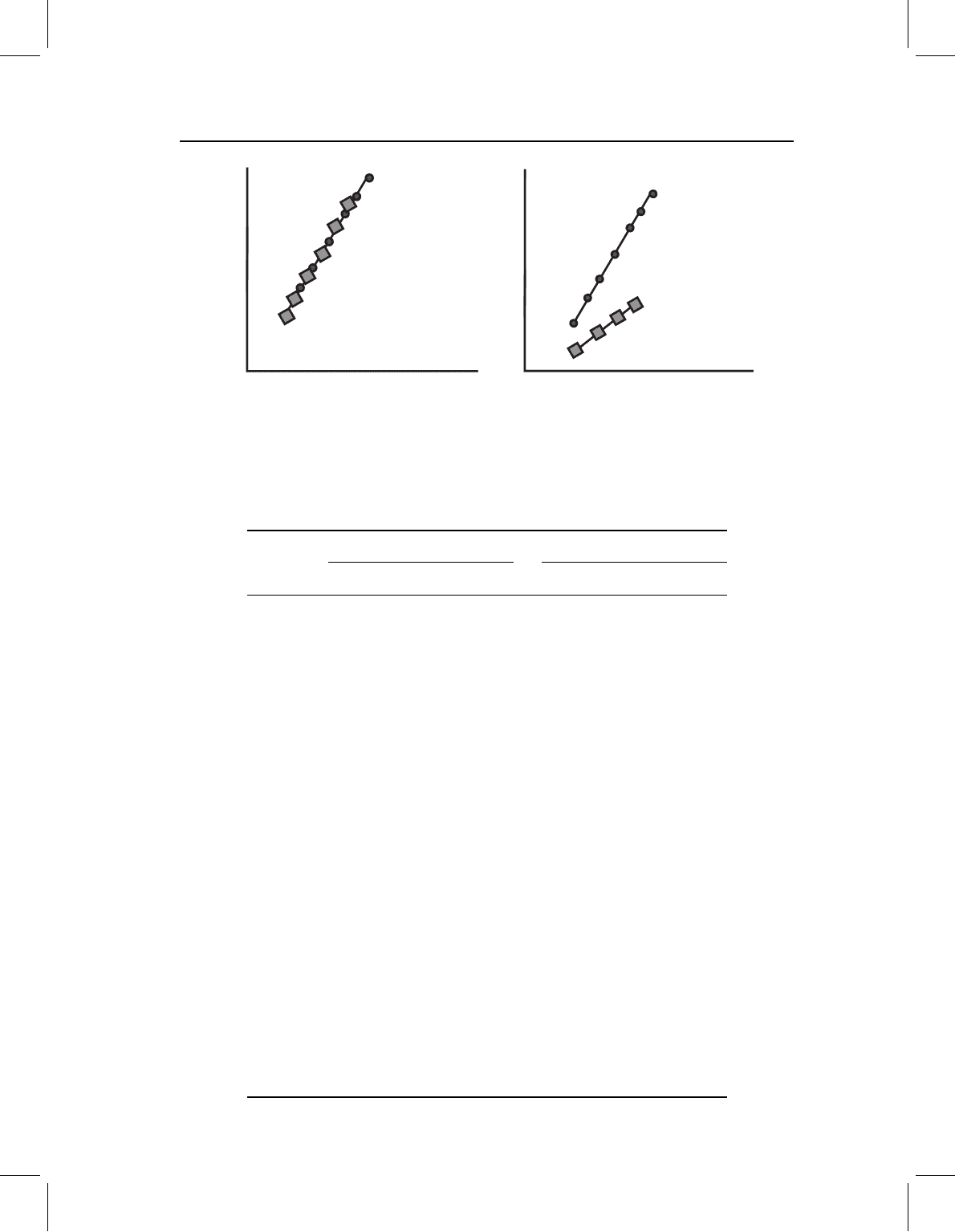
Channeling

To depict the pattern of channeling, we can consider a hypothetical case in which species

have the same shape at the outset of development and follow the same ontogeny of shape,

but differ in the overall rate or timing of development. Graphical evidence of channeling is

shown in Figure 13.19, where we see that the coordinates of the juveniles of the two species

are the same (Figure 13.19A), as are the two ontogenies of shape (Figure 13.19B), but the

trajectories differ in length (Figure 13.19C). Perhaps the most compelling visual evidence

is shown in Figure 13.20 – the descendant adult morphology lies at a subadult position on

the ancestral ontogeny. We can see the coordinates for the descendant’s landmarks in an

intermediate position along the ancestral ontogeny.

The graphical evidence is corroborated by statistical analysis. In a statistical test of

channeling, we would not expect to find a significant difference between the two ontogenies

of shape or in the shape at the youngest comparable phase but we would anticipate a

difference in the length of the ontogenetic vector (the parameter that measures the total

amount of change undergone in each ontogeny over the observed phase). Carrying out these

tests for the hypothetical species depicted in Figure 13.18, we would measure the similarity

between ontogenies of shape by the angle between the (normalized) vector of allometric

coefficients {m

, m

, ...m

}. We find no significant difference between them; the

tiny angle of only 1.8

◦

is not significant compared to the ranges that can be obtained by

resampling within them (4.2

◦

, 7.5

◦

). We also find no significant interspecific difference

between shapes at the outset of the measured phase of development using Goodall’s F-test

(p > 0.999); and the magnitude of the difference between them is a Procrustes distance of

0.0. We do, however, find a significant difference in the length of their ontogenetic vectors

as estimated by the Procrustes distance between youngest and oldest comparable stages; for

the ancestral species that distance is 0.1999 (0.1961–0.2030), whereas for the descendant

it is only 0.109 (0.1055–0.1129). Thus, the descendant’s ontogeny is a truncated version

of the ancestor’s.

chap-13 4/6/2004 17: 28 page 352

352 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

(A)

(B)

(C)

Figure 13.19 Channeling, depicted geometrically (see Figure 13.1 for the same pattern depicted

for traditional measurement data). (A) Superimposed coordinates of juvenile shapes; (B) ontogenies

of shape; (C) lengths of ontogenetic vectors of shape. The two species have the same shape at the

outset of the measured phase, follow the same ontogeny of shape, but differ in the length of their

ontogenetic vectors; the descendant has a truncated version of the ancestral ontogeny.

Figure 13.20 Superimposed coordinates for showing the ontogenetic transformation of ancestral

shape (black circles) and the descendant adult shape (gray squares). The descendant adult shape is

at an intermediate position along the ancestral ontogeny.

chap-13 4/6/2004 17: 28 page 353

THE RELATIONSHIP BETWEEN ONTOGENY AND PHYLOGENY 353

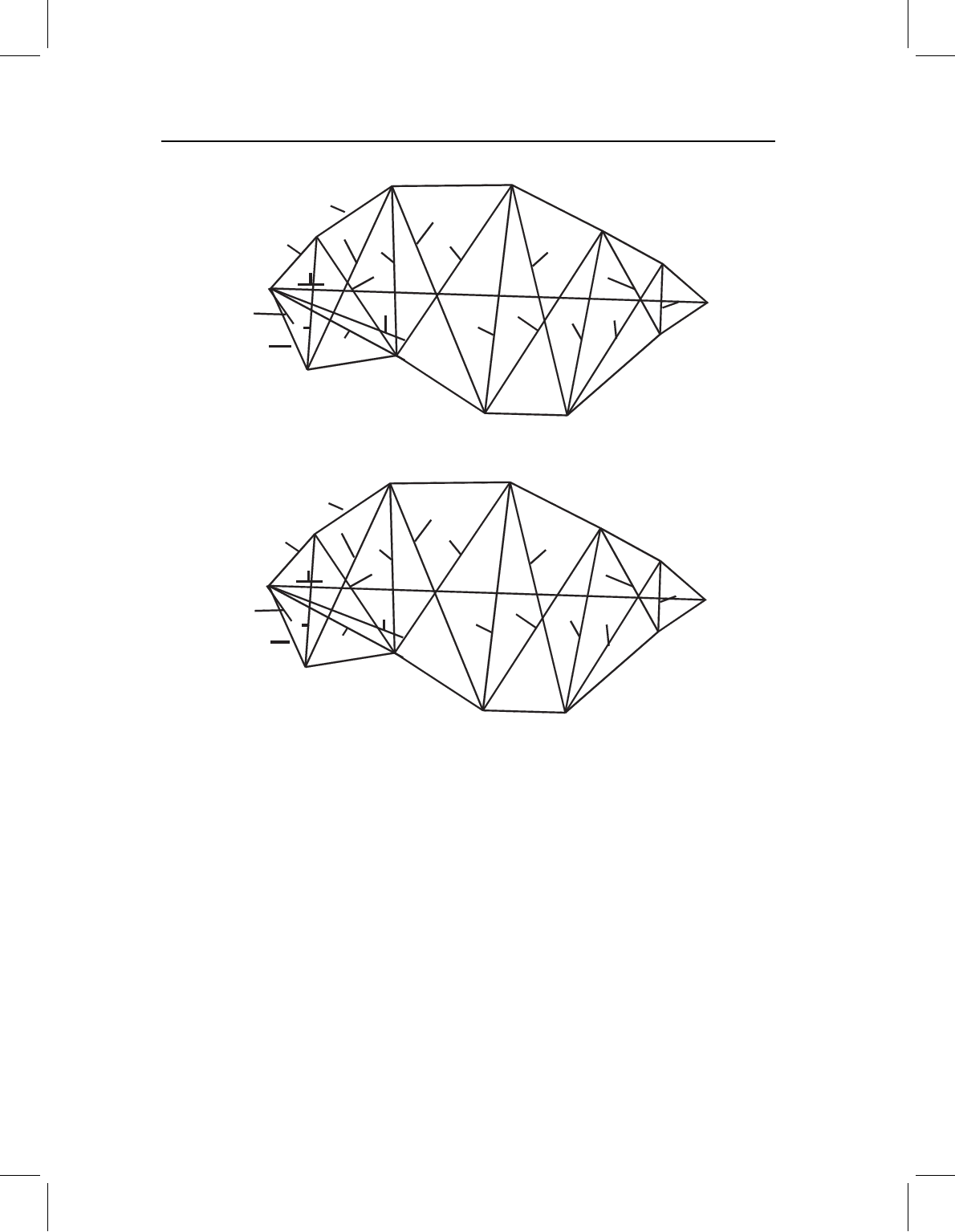
Changes in the ontogenetic trajectory

Changes confined to early morphogenesis

If changes occur solely in early morphogenesis, we would expect that species would be

shaped differently at the youngest comparable stage (Figure 13.21A) but would subse-

quently follow the same ontogeny of form (Figure 13.21B), and to the same extent (Figure

13.21C). To test the hypothesis that only early development is labile, we can show that

there is a significant difference in shape at the outset of the measured phase, but that

any differences in later development are neither significant nor large. For the hypothet-

ical species shown in Figure 13.21, the difference between their shapes at the transition

(B)

(C)

(A)

Figure 13.21 Change confined to early morphogenesis, depicted geometrically (see Figure 13.2

for the same pattern depicted for traditional measurement data). (A) Superimposed coordinates of

juvenile shapes; (B) ontogenies of shape; (C) lengths of ontogenetic vectors of shape. The two species

differ in shape at the outset of the measured phase, but subsequently follow the same ontogeny of

shape and do not differ in the length of their ontogenetic vectors.

chap-13 4/6/2004 17: 28 page 354

354 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

from larval to juvenile phases is highly significant (p < 0.0001) and the Procrustes distance

between their means is large: 0.1247 (0.1196–0.1317). The contrast may seem particularly

striking when we look at the superimposed coordinates and find so little overlap between

species in several of them (Figure 13.21A). As anticipated, there is no significant difference

in their ontogenies of form; the angle between the two vectors is a tiny 1.9

◦

(compared to

the within-species angles of 4.0

◦

and 3.7

◦

). Also as anticipated, the lengths of the ontoge-

netic vectors are the same for both species: 0.1999 (0.1961–0.2030) for the ancestor, and

0.2040 (0.1978–0.2095) for the descendant.

Changes in the spatiotemporal organization of development from the outset

to the end of allometric growth

Should species differ in the spatiotemporal organization of morphogenesis, their ontoge-

netic vectors of shape will differ. It says nothing about shape at the youngest comparable

stage, so the only expectation is that the ontogenies of shape will differ. Rather than dis-

cussing this simple case any further, we will consider the more complex hypotheses that

include it.

Changes in the spatiotemporal organization of development, confined to

late development

Should all change be confined to late morphogenesis, we would expect to see no difference

between the species at the youngest comparable developmental stage (Figure 13.22A),

and a visible difference in their ontogenies of shape (Figure 13.22B). This hypothesis says

nothing about the length of the trajectory of late development; however, changes in length

are due to differences in rate/timing and not to differences in morphogenesis, so we have

drawn trajectories of the same length (Figure 13.22C). For this hypothetical case, juvenile

shapes do not differ (p > 0.999, Procrustes distance =0.0) and neither do the lengths of

the ontogenetic vector: that of the ancestor is 0.1999 (0.1961–0.2030) and that of the

descendant is 0.2011 (0.1977–0.2046). However, as anticipated, the ontogenies of shape

differ significantly; the angle between the two vectors is 32

◦

compared to the range of

within-species angles that can be obtained by resampling (3.7

◦

for both).

Complex changes in multiple parameters and stages

It is difficult to construct hypothetical ontogenies to demonstrate interactions among mul-

tiple parameters, because that requires modeling perturbations of the ontogeny of entire

landmark configurations. Also, the most interesting distinctions among the possibilities

lies in their conflicting predictions about the ontogenetic dynamics of disparity. In par-

ticular, we would wish to distinguish between amplification (which predicts increasing

disparity over ontogenetic time) and counterbalancing (which predicts decreasing dispar-

ity over ontogenetic time). The contrasting patterns are not self-evident in the regression

parameters; distinguishing them requires measuring disparity. Rather than considering

another hypothetical case we will return to the analysis of an empirical case, S. gouldingi

and S. manueli, because our earlier analysis suggested that these species might exemplify

counterbalancing.

chap-13 4/6/2004 17: 28 page 355

THE RELATIONSHIP BETWEEN ONTOGENY AND PHYLOGENY 355

(A)

(B)

(C)

Figure 13.22 Change in the spatiotemporal pattern of development confined to late development,

depicted geometrically. (A) Superimposed coordinates of juvenile shapes; (B) ontogenies of shape;

the measured phase, but subsequently follow different ontogenies of shape; they do not differ in the

length of their ontogenetic vectors.

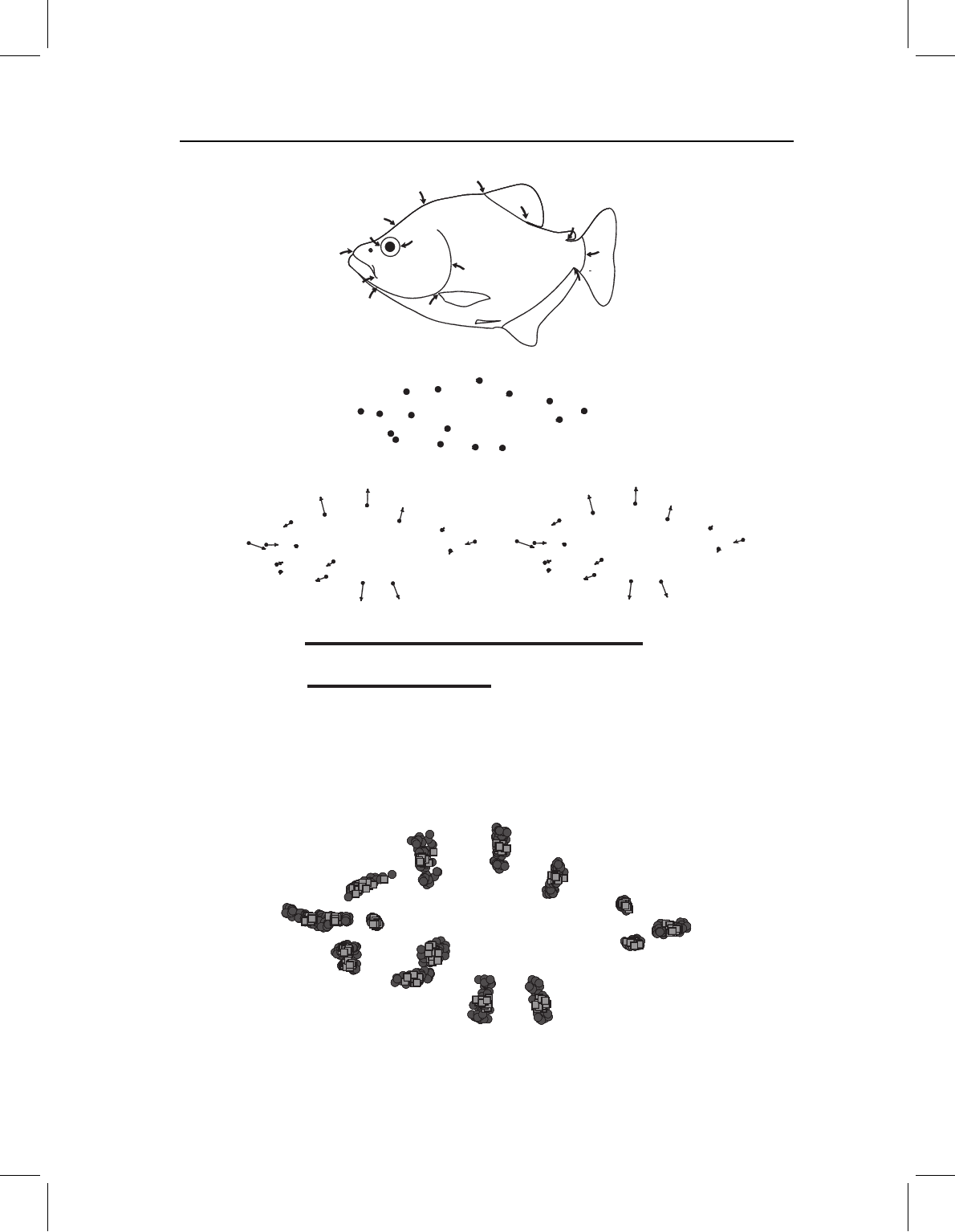
An empirical case: comparing ontogenies of S. gouldingi and S. manueli

Comparing these two species using geometric methods provides compelling graphical

evidence that the species differ in morphology at the transition from larval to juvenile

development (Figure 13.23A), in juvenile morphogenesis (Figure 13.23B), and in length of

their ontogenetic trajectories (Figure 13.23C). The difference in shape at the transition from

larval to juvenile development is statistically significant (p< 0.0001). Moreover, this differ-

ence is not just significant, it is large; the Procrustes distance between mean shapes at that

stage is 0.080 (0.077–0.084). Ontogenies of shape are visibly different and the difference

is statistically significant; the angle between their ontogenetic vectors is 34.9

◦

(compared

to the within-species ranges of 11.0

◦

and 16.6

◦

for S. gouldingi and S. manueli, respec-

tively). The ontogenetic trajectories also differ significantly in length; that of S. gouldingi

chap-13 4/6/2004 17: 28 page 356

356 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

(A)

(B)

(C)

Figure 13.23 Ontogenies of S. gouldingi and S. manueli, depicted geometrically. (A) Superimposed

coordinates of juvenile shapes; (B) ontogenies of shape; (C) lengths of ontogenetic vectors of shape.

The two species differ in shape at the outset of the measured phase (the transition from larval to

juvenile phases), subsequently follow different ontogenies of shape and differ in the length of their

ontogenetic vectors.

is 0.2095 (0.2065–0.2128) and that of S. manueli is 0.1864 (0.01823–0.1906). Therefore,

these two species differ in all three parameters. However, the adults are far less different

than the young juveniles. The Procrustes distance between mean adult shapes is 0.051

(0.047–0.054) – a substantial drop from 0.080. That decrease can be seen in the analysis

of the pooled ontogenies of shape by PCA (Figure 13.24); with increasing age, scores on

PC1 increase, and the two species more closely resemble each other. We can now clearly

see the pattern hinted at in the analysis of traditional morphometric data. The evidence

based on geometric data is stronger, because now there are two distinct eigenvalues, and

PC2 explains 9.5% rather than 0.4% of the variance. Taken together, these results all

demonstrate that the modifications of juvenile development counterbalance those of larval

development, thereby stabilizing adult morphology.

chap-13 4/6/2004 17: 28 page 357

THE RELATIONSHIP BETWEEN ONTOGENY AND PHYLOGENY 357

PC1

PC2

0.04

0.02

⫺0.02

⫺0.04

⫺0.06

⫺0.06 ⫺0.04 ⫺0.02 0.02 0.04 0.06 0.08 0.1

S. gouldingi

S. manueli

Figure 13.24 PCA of the pooled ontogenetic data of S. gouldingi and S. manueli. The two species

differ in shape at the outset of the measured stage (the transition from larval to juvenile phases) and

also in their ontogenies; older specimens are to the right of the plot. The modifications of juvenile

growth appear to counterbalance the change in larval morphogenesis such that the adults are more

similar than the juveniles.

Open questions

Having characterized a variety of evolutionary transformations of ontogeny, obvious

questions are:

1. Which is (are) most likely?

2. Which occur(s) most often?

To answer the first question, we can derive expectations from developmental theory or

functional morphology, or we can even turn to the empirical literature for insights into what

expectations are biologically reasonable. Developmental biology offers few general theo-

ries, but there is a general set of principles that can be useful for framing hypotheses. One

such general principle is that development is likely to be conservative when modifications

disrupt the sequence of epigenetic interactions on which later development depends. Hall

(1992) discusses the importance of epigenetic cascades, and these may resist modification

either because modifications are lethal or because the cascades are internally stabilized.

Stabilizing selection may play an important role in both cases, not only by eliminating

deviants but also by building internal mechanisms that resist such disruptions (internal