Zelditch M.L. (и др.) Geometric Morphometrics for Biologists: a primer

Подождите немного. Документ загружается.

chap-14 4/6/2004 17: 29 page 378

378 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

P. denticulata vs S. gouldingi –

P. denticulata vs S. altuvei

P. denticulata vs S. gouldingi –

P. denticulata vs S. spilopleura

P. denticulata vs S. gouldingi –

P. denticulata vs P. piraya

P. denticulata vs S. gouldingi –

P. denticulata vs S. elongatus

P. denticulata vs S. gouldingi –

P. denticulata vs S. manueli

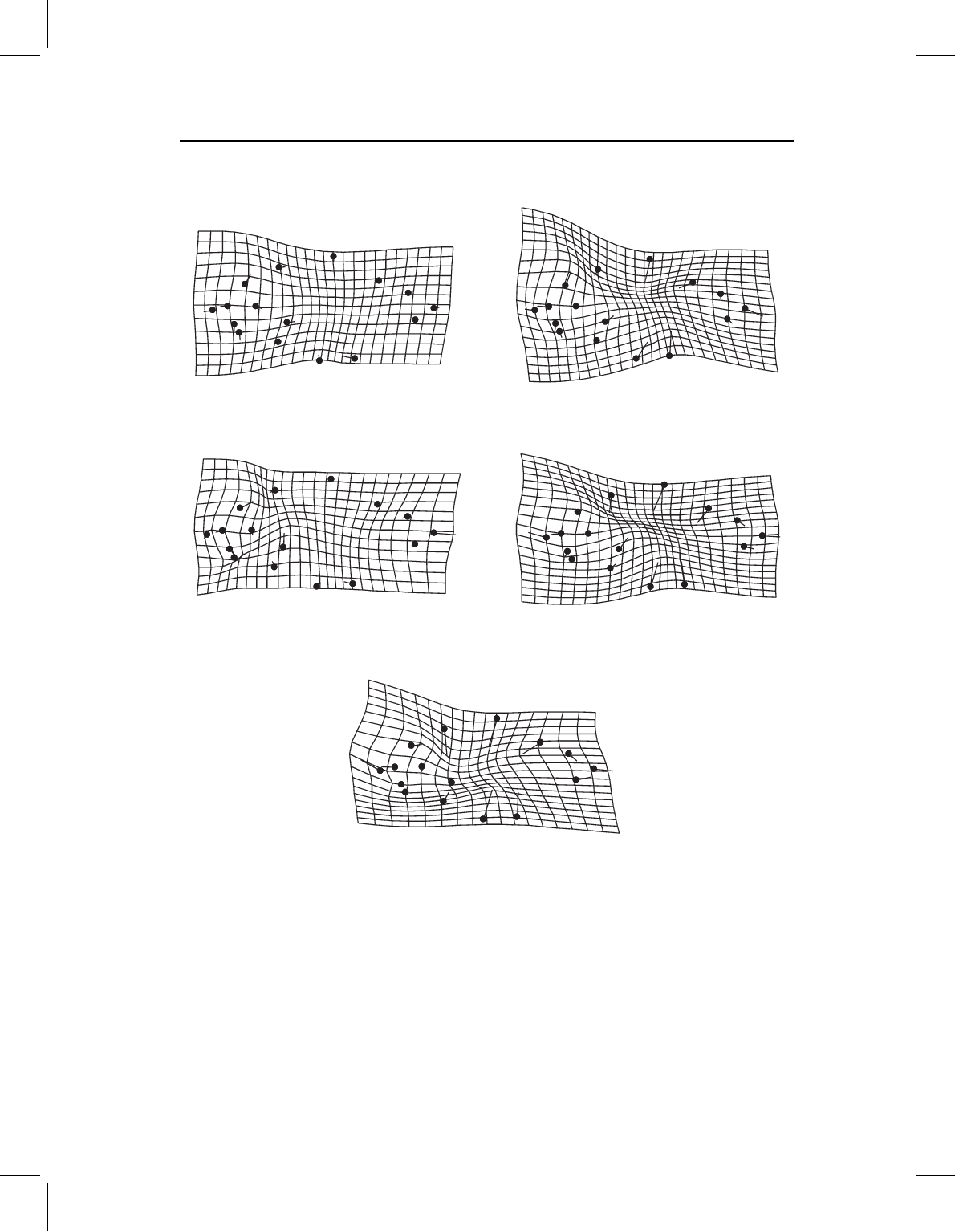
Figure 14.8 Comparisons among vectors describing the difference between P. denticulata and

S. gouldingi, and the vector describing the difference between P. denticulata and each of the other

six species shown in Figure 14.7. Each frame shows the contrast between the two vectors: where

the squares of the grid are square, the two vectors are the same; where the grid shows large differ-

ences, the difference between that species and P. denticulata does not resemble the difference between

P. denticulata and S. gouldingi.

Coding

Having found a character, we can treat it like any other. That is, if using conventional

cladistic methods, we code the characters according to our preliminary judgments of

homology, include it in the data matrix, and analyze that matrix by parsimony. Coding

chap-14 4/6/2004 17: 29 page 379

MORPHOMETRICS AND SYSTEMATICS 379

methods are a contentious subject; systematists vary considerably in their preferred criteria

for coding. The debates have nothing to do with morphometrics except to the extent that

the methods are applied to quantitative data, and that statistical methods are sometimes

favored to decide whether species are different (and should therefore not be coded as hav-

ing a homologous character). The literature on coding is large; interested readers can find

general critiques of coding methods in several papers (e.g. Farris, 1990; Thiele, 1993; Gift

and Stevens, 1997; Swiderski et al., 1998).

Any favored method can be applied to a variable that represents a character. In the

case of “shallow body,” PC1 is a reasonable proxy for the character, so we can apply our

favored method to scores on PC1. It is not so easy to make decisions about characters that

are combinations of several variables because we cannot easily examine the variation within

species in more than two or three dimensions at a time, but doing so may be important

for deciding whether species are similar enough to code their features as homologous.

Coding itself is a subject of debate. Not only are methods for coding controversial, even

the idea of coding is. As mentioned earlier in this chapter, there are methods for inferring

the evolution of shape that do not require coding characters. These methods use a very

different approach to the problem. In particular, they do not make preliminary hypotheses

of homology, then formalize them by codes, then infer the phylogeny that minimizes the net

number of extra steps (a step is considered “extra” if it means that a putatively homologous

character is reinterpreted as arising more than once). Instead, they use explicit models of

the evolutionary process, among which are:

1. Randomly varying directions of natural selection in different lineages

2. Random genetic drift of species around a single, stable optimum

3. Randomly wandering optima

4. Constrained wandering of optima

5. Wandering optima whose paths are correlated, a correlation that diminishes over time

6. Bursts of change around the time of speciation with little or no change thereafter.

(For a more detailed synopsis of the models, see Felsenstein, 2002.) By using one of these

approaches we could avoid the whole issue of coding, but we then have to confront the

problem of deciding which model is reasonable and justifiable. Such models have not

been widely used to infer cladograms from morphological data and, like the methods

which minimize a net morphometric distance (linear or squared) over a tree, model-based

methods might best be considered as methods for reconstructing the evolution of shape

given a cladogram.

Summary

At present, no method is tailored to the problem of finding characters in morphometric

data, and the available methods are cumbersome and involve an uncomfortable degree of

subjectivity. Each could be improved by refining the part of the procedure that involves

making linear combinations of variables, such as combining PC1, PC2 and PC3 to see

whether similarities inferred from scores on one component are belied by scores on others.

However, rather than improving methods that were devised to use standard morphometric

techniques, it might be better to start at the beginning and develop a method tailored to

chap-14 4/6/2004 17: 29 page 380

380 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

our purposes. Doing so will require refining the statement of the problem. Currently we

cannot state the problem in mathematical terms, and that is necessary before we can find

a mathematical solution. Our original statement of the problem focused on one particular

element of it: finding characters without having to dissect organisms arbitrarily into parts

prior to the phylogenetic analysis. However, that dissection need not be an integral part

of a method for finding characters. We could instead use partial least squares analysis

(Chapter 11) to test the hypothesis that the blocks of landmarks do not covary; if they do

not, we can analyze them separately. Even though PLS does not test the hypothesis that a

block constitutes an integrated unit, it may provide a more informed dissection than one

based purely on anatomical conventions.

Clearly, we need additional methodological research – we should not be limited to

the methods currently available when others are feasible. We also need to complement the

methodological investigations by a discussion of what our concepts mean. If we do not, we

may find that we have a rich array of methods that all do something interesting, but none

that do what we intended. It can be bewildering to read discussions about morphometric

characters, because it sometimes appears that nearly every author has a different idea of

the meaning of “character” (as well of “morphometric”). Until we can define “character”

precisely, in terms just as comprehensible to mathematicians as to systematists, we will

not make further progress towards a mathematical solution. We also need more than a

definition of the term; we need to articulate more fully the process by which we find

characters, in general. Most discussions of systematic methods focus on how to analyze

the data, given the data matrix. Our problem is to get that matrix in the first place. One

value of morphometric data is that we find them using mathematical methods, and these

are necessarily explicit. By making our methods of character analysis explicit, just like our

methods of phylogenetic inference, we will enhance the rigor of morphological systematics

in general.

Software

None of the analyses used in this chapter require software beyond that introduced in earlier

chapters. The CVA of the unstandardized data used CVAGen (introduced in Chapter 7);

the analyses of the standardized data used Standard6 to standardize specimens to a com-

mon developmental stage comparable across all taxa (introduced in Chapter 10); then

CVAGen was used to analyze the standardized data. The PCA (of the standardized data)

used PCAGen (also introduced in Chapter 7); to depict changes from one taxon to another

within the plane of two PCs (rather than to depict the directions along the PCs) we placed a

marker on each endpoint of the desired vector, using the Place M1 and Place M2 options,

and depicted the difference between the two endpoints using the Show M2-M1 option.

To describe the differences between each species and another, we first combined the two

files into one, replaced the centroid size by 0 for one species and 1 for the other, then

regressed shape on those codes using Regress6 (introduced in Chapter 10). To compare

the regressions, we saved the vectors, using the option to save the deformation vector

on the File pull-down menu, then input the vectors into VecDisplay (also introduced in

Chapter 10).

chap-14 4/6/2004 17: 29 page 381

MORPHOMETRICS AND SYSTEMATICS 381

References

Adams, D. C. and Rosenberg, M. S. (1998). Partial-warps, phylogeny, and ontogeny: a comment

on Fink and Zelditch (1995). Systematic Biology, 47, 167–172.

Archie, J. W. (1985). Methods for coding variable morphological features for numerical taxonomic

analysis. Systematic Zoology, 34, 236–345.

Chappill, J. A. (1989). Quantitative characters in phylogenetic analysis. Cladistics, 5, 217–234.

Colless, D. H. (1980). Congruence between morphometric and allozyme data for Menidia species:

a reappraisal. Systematic Zoology, 29, 288–299.

Farris, J. S. (1990). Phenetics in camouflage. Cladistics, 6, 91–100.

Felsenstein, J. (2002). Quantitative characters, phylogenies, and morphometrics. In Morphology,

Shape and Phylogeny (N. MacLeod and P. L. Forey, eds) pp. 27–44. Taylor & Francis.

Fink, W. L. and Zelditch, M. L. (1995). Phylogenetic analysis of ontogenetic shape transformations:

a reassessment of the piranha genus Pygocentrus (Teleostei). Systematic Biology, 44, 343–360.

Gift, N. and Stevens, P. F. (1997). Vagaries in the delimitation of character states in quantitative

variation – an experimental study. Systematic Biology, 46, 112–125.

Goldman, N. (1988). Methods for discrete coding of morphological characters for numerical

analysis. Cladistics, 4, 59–71.

Rohlf, F. J. (1998). On applications of geometric morphometrics to studies of ontogeny and

phylogeny. Systematic Biology, 47, 147–158.

Rohlf, F. J. (2002). Geometric morphometrics and phylogeny. In Morphology, Shape and Phylogeny

(N. MacLeod and P. L. Forey, eds) pp. 175–193. Taylor & Francis.

Simon, C. (1983). A new coding procedure for morphometric data with an example from periodical

cicada wing veins. In Numerical Taxonomy (J. Felsenstein, ed.) pp. 378–382. Springer-Verlag.

Swiderski, D. L., Zelditch, M. L. and Fink, W. L. (1998). Why morphometrics isn’t special: coding

quantitative data for phylogenetic analysis. Systematic Biology, 47, 508–519.

Thiele, K. (1993). The holy grail of the perfect character: the cladistic treatment of morphometric

data. Cladistics, 9, 275–304.

Zelditch, M. L., Fink, W. L. and Swiderski, D. L. (1995). Morphometrics, homology and

phylogenetics: quantified characters as synapomorphies. Systematic Biology, 44, 179–189.

chap-14 4/6/2004 17: 29 page 382

chap-15 4/6/2004 17: 29 page 383

PART

Last Things

chap-15 4/6/2004 17: 29 page 384

chap-15 4/6/2004 17: 29 page 385

Beyond two-dimensional configurations

of landmarks

The focus of most of this book has been on the tools for comparing two-dimensional

configurations of landmarks. However, many structures of interest to biologists are three-

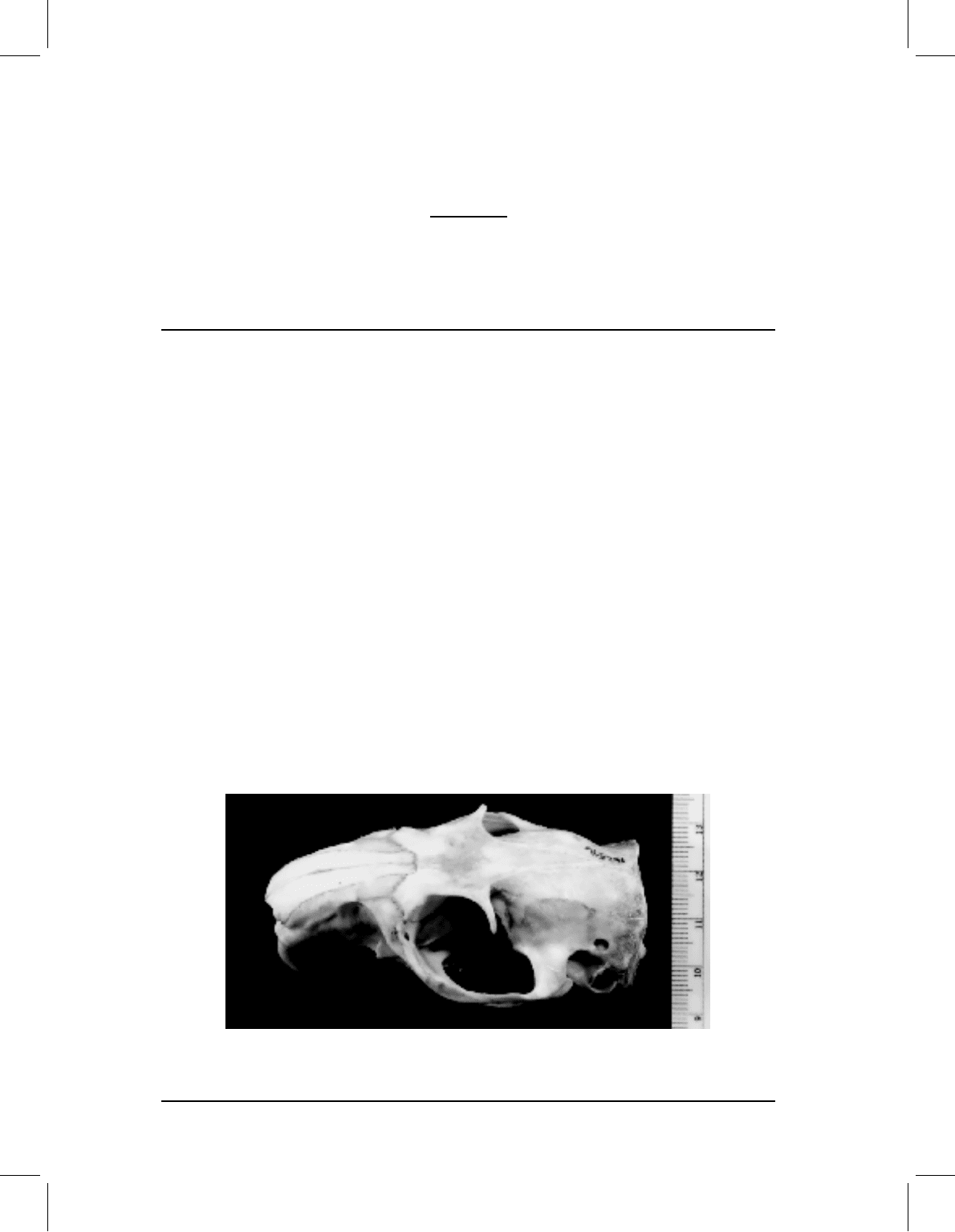
dimensional, or have few landmarks, or both. The skull of a marmot (Figure 15.1), like

that of most mammals, is an example of “both.” The marmot skull is strongly curved

anteroposteriorly and mediolaterally, making it highly three-dimensional (features on the

same bone may be as far apart in the dorsoventral dimension as they are in the mediolateral

or anteroposterior dimensions). In addition, the skull is composed of a small number of rel-

atively large bony plates, so points that can be used as landmarks are sparsely distributed,

occurring primarily at locations where at least three bones meet. In the first part of this

chapter we examine methods that have been devised to analyze three-dimensional con-

figurations of landmarks, and in the second we examine methods that have been devised

to analyze curves and surfaces that lack landmarks. The methods discussed in both parts

Figure 15.1 Skull of a yellow-bellied marmot (Marmota flaviventris), in dorsolateral view,

illustrating curvature of the rostrum, braincase and zygomatic arch.

ISBN 0–12–77846–08 All rights of reproduction in any form reserved

chap-15 4/6/2004 17: 29 page 386

386 GEOMETRIC MORPHOMETRICS FOR BIOLOGISTS

of this chapter have been presented and discussed elsewhere (Bookstein, 1996a, 1996b,

1997a, 1997b; Green, 1996; Sampson et al., 1996; Rohlf and Slice, 1990; Rohlf and

Corti, 2000; Rohlf and Bookstein, 2003). Below, we discuss the general problems and

the advantages and disadvantages of particular approaches. Because most of the software

tools for applying these methods are in the early stages of development, we do not give

detailed instructions for performing particular analyses.

Landmarks in three dimensions

Biological objects (organisms or parts of organisms) are inherently three-dimensional.

Sometimes the third dimension can be ignored as a reasonable simplification – this is

valid if the third dimension is unimportant relative to the other two. For example, dis-

tances between landmarks might be much smaller in the third dimension than in the other

two, so that variation in this dimension contributes little to the description of overall shape

variation (examples include the leaves of many plants, and the bodies of some fish). It is

also possible that the third dimension simply is not relevant to the focus of a particular

analysis. For example, studies of the shape of the lower jaw might focus on the propor-

tions of lever arms associated with various muscles and teeth, and not be concerned with

projections out of the plane of jaw action. However, there are also times when variation

in the third dimension cannot be ignored without losing important information about the

overall pattern of shape variation. As illustrated below, the analysis of landmarks digitized

in three dimensions (X, Y and Z) only requires very simple extensions of the mathematics

principles discussed in previous chapters of this book – there are no new concepts.

The principal obstacles to executing a complete three-dimensional study, from data

collection to publication, are two problems that cannot be solved with mathematics: (1) the

cost of the equipment needed to collect the data, and (2) the difficulty of illustrating three-

dimensional shape differences on static two-dimensional media like the pages of this book.

The solutions to these problems lie in the arts of grant-writing and illustration, so we do

not address them in this book.

Some researchers have proposed clever alternatives to buying expensive equipment for

three-dimensional digitizing (e.g. Spencer and Spencer, 1995; Fadda et al., 1997). Most

of these alternatives involve collecting a series of overlapping images at different angles;

some use mirrors, others rotate the specimen as if it were on a rotisserie. Landmarks are

digitized in each two-dimensional image, and then the angle between two images is used

to compute a set of three-dimensional coordinates from the two sets of two-dimensional

coordinates for the landmarks present in both images. Similar triangulation schemes are

used in some commercial digitizers.

The problem with a triangulation technique is that the uncertainty of the third coordi-

nate (Z) is produced by a combination of three different potential errors: (1) error in digiti-

zing the first two coordinates (X, Y) of the landmarks in the overlapping views; (2) error

in measuring the angle between images; and (3) error in measuring the distance from the

specimen to the camera lens. The compounding of these errors means that the computed

third coordinate is likely to have a much larger error than the two directly observed coor-

dinates; it also means that the error in the third coordinate is not independent of the errors

in the first two coordinates. In commercially produced digitizers the confidence interval

chap-15 4/6/2004 17: 29 page 387

BEYOND TWO-DIMENSIONAL CONFIGURATIONS OF LANDMARKS 387

for the Z-coordinate is about twice as large as those for the X- and Y-coordinates, which

is tolerable only because all of the confidence intervals are extremely small. In home-made

equipment the difference between confidence intervals is likely to be larger, because the

angle and distance cannot be controlled or measured with the same precision. These prob-

lems are exacerbated when more than two images are chained together to expand the

coverage of the object. The progressive change in the orientation of the object (or camera)

relative to a fixed coordinate system causes a progressive shift in the relative uncertain-

ties of the coordinates. For example, the first pair of images might be used to infer the

Z-coordinates of the landmarks from the X- and Y-coordinates, but the last pair of images

might be used to estimate the Y-coordinates of the landmarks in those images from X-

and Z-coordinates. Consequently, different landmarks will have different combinations of

errors affecting estimation of coordinates on the same axis. For these reasons, we strongly

recommend that you buy reliable commercial equipment designed for three-dimensional

analysis if you think that such analyses will be necessary to fully describe shape variation

in your data.

If the cost of equipment is absolutely out of reach, or you want to conduct a pilot

project to investigate the need for such expenditure, we recommend using partial least

squares (PLS). We have already presented a detailed discussion of PLS and illustrated its

use to analyze the covariance of shape changes seen in different regions of the same lateral

view of piranhas (Chapter 12). Rohlf and Corti (2000) present an example in which PLS

is used to analyze the covariance of shape changes seen in dorsal and ventral views of

skulls of the house mouse (Mus musculus). When the same procedure is used to analyze

the covariance of shape changes seen in less divergent views (e.g. dorsal and lateral), the

pictures of the correlated shape changes will be pictures of a three-dimensional change.

Superimposing configurations of landmarks

As in two-dimensional shape analyses, the first step after collecting the data is a general-

ized least squares Procrustes superimposition (GLS) to remove those differences between

configurations that are not differences in shape. Differences in location, scale and orien-

tation of three-dimensional configurations are removed by exactly the same operations

that are used to superimpose two-dimensional configurations (translation, scaling and

rotation); the only substantive difference is that superimposing three-dimensional config-

urations forces us to work with larger matrices. Just as the coordinates of K landmarks

in two dimensions are represented as a K ×2 matrix, the coordinates of K landmarks in

three dimensions are represented as a K ×3 matrix:

A =













(15.1)

The same operations will be performed on these matrices of three-dimensional landmarks

as are performed on matrices of two-dimensional landmarks. In addition, most formulae

used to perform these operations will have the same general form as those used in analyses